- ... 1
- This work was supported in part by DARPA and the NSF.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... pearl'').2
- We have released Version 4.2,
see http://www.cs.cornell.edu/Info/Projects/NuPrl/nuprl.html. Version 5 and
``MetaPRL will be available at this World Wide Web site in 1999.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
mathematics.3
- Begriffsschrift (``concept script'') analyzed the
notion of a proposition into function and argument, introduced the
quantifiers, binding, and a theory of identity. This created the entire
predicate calculus. Grundgesetze presented a theory of classes based
on the comprehension principle and defined the natural numbers in terms of
them.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... methods.4
- I refer to Hilbert's formalist
program founded on a finitistic analysis of formal systems to prove their
consistency and to justify non-constructive reasoning as a (possibly
meaningless) detour justified by the consistency of a formal
system.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Hilbert.5
- Gödel showed that consistency is
not sufficient to justify the detour because there are formulas of number
theory such that both P and
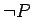 can be consistently added (P an
unprovable formula).
can be consistently added (P an
unprovable formula).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
incidental.6
- Principia is not formal in the modern sense.
There are semantic elements in the account which [118,117] objected
to. Hilbert made a point of formalizing logic, and we follow in that
purely formal tradition.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...[6]).7
- This capability can be
explored at the Nuprl project home page
www.cs.cornell.edu/Info/Projects/NuPrl.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... language.8
- There are, of course, opposing
views; [118,117] was concerned with sentences or formulas as
is [99], and we access propositions through specific formulas.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...Prop.9
- In topos theory Prop and the true propositions
form the subobject classifier,
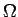 ,
,
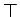 see
[10,78,72].
see
[10,78,72].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...[80,28]).10
- In
topos theory this leads to the Grothendieck topos which is definable in
our predicative type theory of section 3.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... true.11
- In Martin-Löf's theorem these judgments are prior to
assertion; in Nuprl they can be simultaneous with assertion.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... activity.12
- But the consequences of finding a proof or a
disproof can be very concrete and very significant. For instance, a
purported proof might cause someone to test a device in the belief that it is
safe to do so. If the proof is flawed, the device might destroy something of
great value.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... it.13
- When we need to present evidence for a
typing judgment, we will incorporate that into our proofs as well and speak
of proving a typing. One might want to give this a special name, such as a
derivation, but in Nuprl we use the term proof. These typing
``proofs'' never have interesting computational content.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
completeness.14
- [73] tries to express this uniformity using
permutations.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....15
- We will deal later
with the issue of equality on Prop, which seems necessary to talk about
functions.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 17
- <
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 16
- Since we do not study any mapping of formulas
to pure propositions, I have not worried about relating elements of
Pn and Pm, n<m, by coherence conditions.
Then given
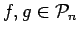 and given any lifted connective op, we have
and given any lifted connective op, we have
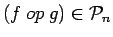 .
Nothing else belongs to
.
Nothing else belongs to
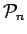 .
When
we want to mention the underlying type, we write
.
When
we want to mention the underlying type, we write
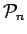 as
as
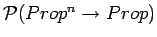 .
Let
.
Let
 ;
these are the pure
propositionspure proposition. Note that
;
these are the pure
propositionspure proposition. Note that
 is inductively
defined. The validvalid element elements of
is inductively
defined. The validvalid element elements of 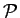 are
those functions
are
those functions
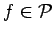 such that for
such that for
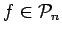 and
and
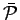 any element of
any element of
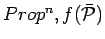 is true.
Call these
is true.
Call these
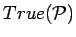 .
.
Using these concepts we can express the idea of a uniform functional proof.
The simplest approach is probably to use a Hilbert style axiomatic base. If
we take Heyting's or Kleene's axioms for the intuitionistic propositional
calculus, then we can define
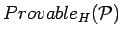 inductively. The
completeness theorem we want is then
inductively. The
completeness theorem we want is then
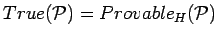 .
.
We can use the same technique to define the pure typed propositional functions.
First we need to define pure type functionspure typed function
 as a subset of Type
as a subset of Type
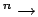 Type for
Type for
 .
We
take
.
We
take 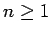 since there are as yet no constant types to include. An
example is
since there are as yet no constant types to include. An
example is
 .
Next we define the typed propositional
functions
.
Next we define the typed propositional
functions
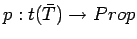 .
.
In general we need to consider functions whose inputs are n-tuples of the
type
and whose output is a Prop. We do
not pursue this topic further here, but when we examine the proof system for
typed propositions we will see that it offers a simple way to provide abstract
proofs for pure typed propositions that use only rules for the connectives and
quantifiers -- say a pure proofpure proof. There are
various results suggesting that if there is any proof of these pure
propositions, then there is a pure proof. These are completeness
results for this typed version of the predicate calculus. We will not prove
them here.
17#552#>Since we do not study any mapping of formulas
to pure propositions, I have not worried about relating elements of
Pn and Pm, n<m, by coherence conditions.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
display.18
- This is the mechanism used in Nuprl and HOL; PVS uses
multiple conclusion sequents.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
argument.19
- Although if functional equality is defined intensionally,
then it is also possible to analyze their structure. Of course, function can
also be passed as data.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
axioms.20
- ``AutomathAutomath is a language which we claim to
be suitable for expressing very large parts of mathematics, in such a way
that the correctness of the mathematical contents is guaranteed as long as
the rules of the grammar are obeyed.'' [40].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... rules.21
- The associated tactics are attached as well,
see [61,62].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
axioms.22
- The associated tactics can also enforce global constraints on
the theory such as ``decidable type checking.''
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...metatheory.23
- That it had to be so was part of Hilbert's
Program for a formal foundation of mathematics. Classical parts of
mathematics were to be considered as ideal elements ultimately justified by
constructive means.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... proofs.24
- ``...we extend the language by proclaiming that proofs of one and
the same proposition are always definitionally equal. This extra rule was
called `proof irrelevance'....''
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... apparatus.25
- This is quite different
from taking them to be metamathematical objects as is done in proof
theory...a theory that could be formalized in Automath.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...axiom.26
- In Martin-Löf type theory and in
Nuprl all proofs of atomic formulas are reduced to a token (axiom in
Nuprl). Information that might be needed from the proof is kept only at
the metalevel.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...[24]).27
- For Brouwer this language is
required by an individual only because of the limits and flaws in his or her
mental powers. But for our theory, language is essential to the
communication among agents (human and artificial or otherwise) needed to
establish public knowledge.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... objects.28
- The
interplay between expressions and objects has seemed confusing to readers of
constructive type theory. In my opinion this arises mainly from the fact
that computability considerations cause us to say more about the underlying
language than is typical, but the same relationship exists in any formal
account of mathematics.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
term.29
- Martin-Löf would only need the premise
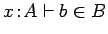 since this means that A is a type. But in his
system to prove
since this means that A is a type. But in his
system to prove
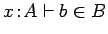 requires proving
requires proving
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
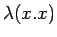 .30
.30
- We could also use
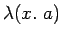 for any
for any 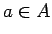 if there is one since under the assumption that
if there is one since under the assumption that 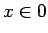 ,
x=a for
any a, thus
,
x=a for
any a, thus
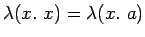 in
in
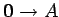 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....31
-
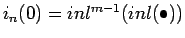 and
and
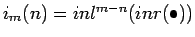 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... product.32
- Martin-Löf calls this a
dependent sum and writes
 .
We think of it as a
generalization of
.
We think of it as a
generalization of 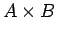 and display the constructor in Nuprl as
and display the constructor in Nuprl as
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
![]() and given any lifted connective op, we have
and given any lifted connective op, we have
![]() .
Nothing else belongs to
.
Nothing else belongs to
![]() .
When
we want to mention the underlying type, we write
.
When
we want to mention the underlying type, we write
![]() as
as
![]() .
Let
.
Let
 ;
these are the pure
propositionspure proposition. Note that
;
these are the pure
propositionspure proposition. Note that
 is inductively
defined. The validvalid element elements of
is inductively
defined. The validvalid element elements of ![]() are
those functions
are
those functions
![]() such that for
such that for
![]() and
and
![]() any element of
any element of
![]() is true.
Call these
is true.
Call these
![]() .
.
![]() inductively. The
completeness theorem we want is then
inductively. The
completeness theorem we want is then
![]() .
.
![]() as a subset of Type
as a subset of Type
![]() Type for
Type for
![]() .
We
take
.
We
take ![]() since there are as yet no constant types to include. An
example is
since there are as yet no constant types to include. An
example is
![]() .
Next we define the typed propositional
functions
.
Next we define the typed propositional
functions
![]() .
.