Duality and disjoint unions

dualitydisjoint union The types 0 and 1 are called dualsdual of each other in a category theory. Here is what this means. The object 1 is called terminalterminal (or finalfinal) because for every type A, there is a unique map in $A \rightarrow$ 1, i.e. a map terminating in 1, namely $\lambda(x.\ \bullet)$. The object 0 is initialinitial since for every type A, there is a unique map initiating in 0, i.e. 0 $\rightarrow A$, namely $\lambda(x. x)$.³⁰

The dualitydual concept is that the arrows of the types are reversed in the definition.

1 is final iff for all A there is a unique element in $A \rightarrow \mathbf{1}$.

0 is initial iff for all A there is a unique element in $\mathbf{0} \rightarrow A$.

We will examine another useful duality next.

The type $A \times B$ can be characterized in terms of functions. In category theory this is done with a diagramproduct type

	C
f $\swarrow$	$\stackrel{\vdots}{\vee}p$	$\searrow$ g
A $\stackrel{a}{\leftarrow}$	$A \times B$	$\stackrel{b}{\rightarrow} B$

which says that given the projection functions $a==\lambda(x.1o\!f(x))$, $b==\lambda(x.2o\!f(x))$ and any functions $f:C \rightarrow A$, $g:C \rightarrow B$, there is exactly one map p denoted $\left\langle f, g\right\rangle \in C \rightarrow A \times B$such that $f=a \circ p$ and $g=b \circ p$; that is, for $z \in C$

$f(z)=a(\langle f, g\rangle (z))$

$g(z)=b(\langle f, g\rangle (z))$.

We can show that $\lambda(z. pair(f(z); g(z)))$ is the unique map $\langle f, g\rangle$.

In category theory there is a construction that is dual to the product, called co-productco-product type. Duals are created by reversing the arrows in the diagram, so for a dual we claim this.

	C
f $\nearrow$	$\stackrel{\wedge}{\vdots}p$	$\nwarrow$ g
A $\stackrel{inl}{\rightarrow}$	A + B	$\stackrel{inr}{\leftarrow} B$

Given A, B with maps $inl \in A \rightarrow A+B$, $inr \in B\rightarrow A+B$and maps $f \in A \rightarrow C$, $g \in(B\rightarrow C)$ there is a unique map $[f, g] \in A+B \rightarrow C$ such that

$$[f, g]\circ inl = f\ \ \ \mbox{and}\ \ \ [f, b] \circ inr=g.$$

In type theory we take inl(a), inr(b) to be canonical values with evaluation

$$inl(a)\ evals\_to\ inl(a)\ \ \ \ \ inr(b)\ evals\_to\ inr(b).$$

For A and B types, A+B is a new type called the disjoint uniondisjoint union of A and B. But the typing rules present a difficulty. If we simply write

$$\frac{a = a'\ \mbox{in}\ A}{inl(a) = inl(a')\ \mbox{in}\ A+B}... ... \frac{b = b'\ \mbox{in}\ B}{inr(b) = inr(b')\ \mbox{in}\ A+B}$$

then we can deduce a judgment like $inl(0) = inl(0)\ \mbox{in}\ {{\mathbb{N} }} + suc(0)$ which does not make sense because ${{\mathbb{N} }} + suc(0)$ is not a type. That is, the rules would no longer propagate the invariant that if $t = t\ \mbox{in}\ T$ then T is a type.

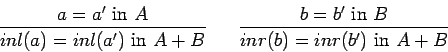
We could solve this problem by including a new judgment, $T\ is\_a\ type$, into the theory. The rules would be quite clear for the types already built, namely:

$${{\mathbb{N} }}\ is\_a\ type\ \ \ \mathbf{1} \ is\_a\ type\ \ \ \mathbf{0}\ is\_a\ type$$

$A\ is\_a\ type\ \ \ \ B\ is\_a\ type$

        $(A \times B)\ is\_a\ type$

        $list(A)\ \ \ \ is\_a\ type$

        $(A \rightarrow B)\ \ is\_a \ type$

        $(A+B)\ \ is \_a\ type$

We can then use the rules

$$\frac{a = a'\ \mbox{in}\ A\ \ \ \ \ B\ is\_a\ type}{inl(a) = ... ... B\ \ \ \ \ A\ is\_a\ type}{inr(b) = inr(b')\ \mbox{in}\ A+B}$$

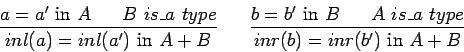
We will see in section 3.4 how to avoid adding this new judgment $T\ is\_\ type$.

The map [f, g] is built from a new form called decide(d; u.f(u); v.g(v)) whose evaluation rules are

$$\frac{f(a)\ evals\_to\ c}{decide(inl(a); u.f(u); v.g(v))\ evals\_to\ c}$$

$$\frac{g(b)\ evals\_to\ c}{decide(inr(b); u.f(u); v.g(v))\ evals\_to\ c}$$

The function [f, g] is $\lambda(x. decide(x; u.f(u); v.g(v)))$. It is easy to see that

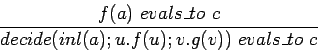
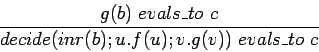
[f, g](inl(a))=f(a) and

[f, g](inr(b))=g(b).