Functions

function

The judgment $x = x\ \mbox{in}\ A \vdash b=b\ \mbox{in}\ B$ defines a function from A to B whose rule is given by the expression b. We know this from the functionality constraint implicit in the judgment, i.e. if a=a' in the type A, then b[a/x]=b[a'/x] in the type B. Likewise if b₁ is an expression in x and b' is an expression in x' then $x = x'\ \mbox{in}\ A \vdash b = b'\ \mbox{in}\ B$ defines such a function. The two rules b, b'are considered equal on equal a, a' in A. Also it is part of the judgment that b[a/x]=b'[a'/x']. To this extent at least the notion of equality on these functions is extensional.

Let us look at patterns of functionality that involve functions as arguments. The addition function on N is represented by

$$z \in N \times N \vdash add(1o\!f(z); 2o\!f(z)) \in N$$

We also know that

$$l \in list(N) \vdash addL(l) \in N.$$

We know that the pattern of definition used to form addL, multL, expL can be extended to any binary function f from $N \times N$ to N using fL_k(l)=L(l; k; h, t, a. f(h, a)). For any specific f we can write this function fL_k(l), but we would like to express the general fact as a function of f, saying: for any function from $N \times N$ to N and any k in N, L(l; k; h, t, a. f(h, a)) is a functional expression in l, k and f.

In order to say this, we need a type for f. The notation $(N\times N) \rightarrow N$ is the type used in section 2. We can add $(A \rightarrow B)$ as a type expression for A and B types. But we also need canonical values for the type, what should they be? Can we use $(x \in A \vdash b \in B)$ as a notation for a function in $(A \rightarrow B)$?

It would be acceptable to use just that notation; it is even similar to the Bourbaki notation $x \mapsto b(x \in A, b \in A)$ (see [15]). But in fact we do not need the type information to define the evaluation relation nor to describe the typing rule. So we could simply use $(x \mapsto b)$. Instead we adopt the lambda notation $\lambda(x.b)$ more familiar in computer science as we did in sections 1 and 2.

We also need notation for function application. We write ap(f; a) for the application of function f to argument a, but often display this as f(a). The new evaluation rules are:

$$\lambda(x.b)\ evals\_to\ \lambda(x. b)$$

$$\frac{b[a/x]\ evals\_to\ c}{ap(\lambda(x.b); a)\ evals\_to\ c}$$

The typing rule is

$$\frac{x=x'\ \mbox{in}\ A \ \vdash\ b=b'\ \mbox{in}\ B}{\lambda(x.\: b) = \lambda(x'.\: b')\ \mbox{in}\ (A \rightarrow B)}$$

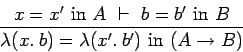
This rule generates the type $(A \rightarrow B)$ as a term.²⁹