The types defined so far belong to an inductively defined collection according
to the scheme for
![]() in the last section. Let U1 denote this
inductively defined collection of types; it has the characteristic of a type in
that it has elements and is structured. Evaluation is defined on the elements,
e.g.
in the last section. Let U1 denote this
inductively defined collection of types; it has the characteristic of a type in
that it has elements and is structured. Evaluation is defined on the elements,
e.g.
![]() ,
,
![]() ,
etc. So all of the elements are canonical and are
built up inductively themselves. In this regard U1 resembles
,
etc. So all of the elements are canonical and are
built up inductively themselves. In this regard U1 resembles
![]() .
It
has all the properties of a type.
.
It
has all the properties of a type.
We want to make U1 a type. So we add rules for its elements in
terms of equalities. For example, there are rules
![]() and
and
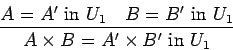
The equality rules we have in mind are these
| A=A' in U1 B=B' in U1 |
|
|
|
|
|
|
| (A+B) = (A'+B') in U1 |
This is a structural or intensional equality (used in both Nuprl and
[80]). It turns out that this equality is also extensional since A=Bin U1 iff ![]() implies
implies ![]() and conversely. This is the only type
so far whose elements are types, but it does not include all
types, in particular U1 is not in U1 according to our semantics.
and conversely. This is the only type
so far whose elements are types, but it does not include all
types, in particular U1 is not in U1 according to our semantics.
We have no way to prove that U1 is not in U1. We don't even have a way to say this. But it would be possible to add a recursion combinator on U1 that expressed the idea that U1is the least type closed under these operations. The combinator would have the form of a primitive recursive definition
| f(, x) = b0(x) | |
| f(1, x)=b1(x) | |
| f(N, x)=b2(x) | |
|
|
|
| f((A+B), x)=h4(A, B, f(A, x), f(B, x)) |
With this form of recursion and the corresponding induction rule we could prove that every element of U1 was either 0, 1, N, a product, a union, etc.
Once we can regard types as elements of a type like U1, then we can extend
our methods for building objects, say over
![]() or by case analysis over a
type of Booleans, say
or by case analysis over a
type of Booleans, say
![]() etc. to building types. Here are two examples,
taking
etc. to building types. Here are two examples,
taking
![]() as an abbreviation of
1 + 1 and
abbreviating
as an abbreviation of
1 + 1 and
abbreviating
![]() as tt and
as tt and
![]() as
as ![]() .
.
Let
T(tt)=A, T(ff)=B, then
![]() is a function
is a function
![]() .
If we build a generalization of
.
If we build a generalization of
![]() to n distinct
values, say
to n distinct
values, say
![]() n times
defined by
n times
defined by
![]() with
elements
with
elements
![]() ,
then we can build a function T(x) selecting n
types, T(ib).
,
then we can build a function T(x) selecting n
types, T(ib).
It is worth thinking harder about functions like
![]() .
This is an indexed collection of types,
.
This is an indexed collection of types,
![]() .
We can imagine putting them together to
form types in various ways, for instance by products or unions or
functions
.
We can imagine putting them together to
form types in various ways, for instance by products or unions or
functions
|
|
|
|
|
|
|
|
We could define these types recursively, say by functions ![]() ,
,
![]() and
and ![]() if we could have inputs like this: m in
if we could have inputs like this: m in
![]() ,
T in
,
T in
![]() ,
,
|
|
|
|
|
In the case of ![]() and
and ![]() the operations make sense even for
infinite families of types, say indexed by
the operations make sense even for
infinite families of types, say indexed by
![]() for any type A. We can think of
for any type A. We can think of ![]() over
over
![]() as functions f such that on input
as functions f such that on input ![]() ,
we have
,
we have
![]() .
For
.
For ![]() over
over
![]() we can use the
elements a as ``tags'' so that elements are pairs
we can use the
elements a as ``tags'' so that elements are pairs
![]() where
where
![]() .
.
These ideas give rise to two new type constructors, ![]() and
and ![]() over an indexed family of types
over an indexed family of types
![]() .
We write
the new constructors as
.
We write
the new constructors as ![]() and
and
![]() .
We could use
typing rules like these
.
We could use
typing rules like these
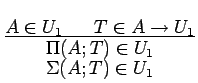
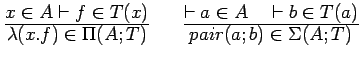
With ![]() and
and ![]() and using induction over
and using induction over
![]() we can build types
that are not in this U1. For example, let
we can build types
that are not in this U1. For example, let
![]() .
Then f is a function
.
Then f is a function
![]() where
where
![]() taken n times. The actual function is
taken n times. The actual function is
![]() .
Now we can build types like
.
Now we can build types like
![]() and
and
![]() which are
not in U1. We could imagine trying to enlarge the inductive type class
U1 by adding these operators to the inductive definition. We will take up
this topic in the next section.
which are
not in U1. We could imagine trying to enlarge the inductive type class
U1 by adding these operators to the inductive definition. We will take up
this topic in the next section.