The traditional approach to studying logic is to first isolate the propositional calculus and then the first-order predicate calculus, and to study completeness results for these calculi, since completeness results tie together the semantic and proof-theoretic concepts. These topics are covered by defining restricted formal languages. We will take this approach to typed logic starting in section 2.4 on formulas. But many of the concepts can also be presented by a mathematical analysis of propositional functions without resort to linguistic mechanisms and formulas.
There is one outstanding technical problem about the propositional calculus which benefits from this direct analysis, namely a functional approach to completeness of the intuitionistic propositional calculus. The most widely known completeness theorem for this calculus is based on Kripke semanticsKripke semantics ([71]); this account of propositional calculus semantics, while illuminating and technically elegant, and even constructively meaningful, is not faithful to constructive semantics. In particular, it is not based on the type-theoretic semantics we offer in part 3. Providing a completeness result for a constructively faithful semantics is an open area, and it seems to me that Martin-Löf's inductive semantics has created new opportunities here to produce definitive results.
The key to a constructive semantics might be a careful study of a functional approach to propositions that allows us to express the functional uniformity of proofs that is central to completeness.14 As a start, we can try to understand the basic concept of a pure propositional function without resort to formal languages.
Consider a propositional function of one argument,
![]() .
This can
be understood as a function from Prop to Prop.15 The function
.
This can
be understood as a function from Prop to Prop.15 The function
![]() in
variables P, Q is a two-argument function, most naturally from Prop to
in
variables P, Q is a two-argument function, most naturally from Prop to
![]() as would be clear from writing the function as
as would be clear from writing the function as
The idea is to define the pure propositional functions
pure propositional function inductively as a subtype of
![]() constructed using only constant functions, simple projections
like
constructed using only constant functions, simple projections
like
![]() and the operations
and the operations
![]() lifted up to the level of functions.
lifted up to the level of functions.
Each connective
![]() can be lifted to the functions
can be lifted to the functions
![]() ,
namely given f and g, define
,
namely given f and g, define
![]() where
where
![]() .
For
example, if
f(P, Q) = P and
.
For
example, if
f(P, Q) = P and
![]() then
then
![]() is a function h such that
is a function h such that
![]()
We can now define the general abstract propositional functions of n variables
call the class
![]() as the inductive subset of
as the inductive subset of
![]() whose base elements are the constant and projection functions,
whose base elements are the constant and projection functions,
|
|
|
|
|
|
where
|
Then given
![]() and given any lifted connective op, we have
and given any lifted connective op, we have
![]() .
Nothing else belongs to
.
Nothing else belongs to
![]() .
When
we want to mention the underlying type, we write
.
When
we want to mention the underlying type, we write
![]() as
as
![]() .
Let
.
Let
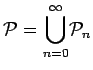 ;
these are the pure
propositionspure proposition. Note that
;
these are the pure
propositionspure proposition. Note that
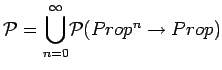 is inductively
defined. The validvalid element elements of
is inductively
defined. The validvalid element elements of ![]() are
those functions
are
those functions
![]() such that for
such that for
![]() and
and
![]() any element of
any element of
![]() is true.
Call these
is true.
Call these
![]() .
.
Using these concepts we can express the idea of a uniform functional proof.
The simplest approach is probably to use a Hilbert style axiomatic base. If
we take Heyting's or Kleene's axioms for the intuitionistic propositional
calculus, then we can define
![]() inductively. The
completeness theorem we want is then
inductively. The
completeness theorem we want is then
![]() .
.
We can use the same technique to define the pure typed propositional functions.
First we need to define pure type functionspure typed function
![]() as a subset of Type
as a subset of Type
![]() Type for
Type for
![]() .
We
take
.
We
take ![]() since there are as yet no constant types to include. An
example is
since there are as yet no constant types to include. An
example is
![]() .
Next we define the typed propositional
functions
.
Next we define the typed propositional
functions
![]() .
.
In general we need to consider functions whose inputs are n-tuples of the
type