


Next: Type theory
Up: Typed logic
Previous: Proofs as objects
Heyting's semantics
Here is Heyting's interpretationHeyting's semantics
of the judgment
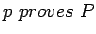 .
.
- 1.
- For atomic P we cannot base the explanation on propositional
components of P because there aren't any. But it might depend on
an analysis of terms and their type which could be compound.
We recognize certain atomic propositions, such as
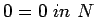 as
``atomically true.'' That is, the proofs are themselves atomic, so the
proposition is an axiom. In the case when the terms are atomic and the type
is as well, there is little left to analyze. But other atomic propositions
can be reduced to these axioms by
computation on terms, say
as
``atomically true.'' That is, the proofs are themselves atomic, so the
proposition is an axiom. In the case when the terms are atomic and the type
is as well, there is little left to analyze. But other atomic propositions
can be reduced to these axioms by
computation on terms, say
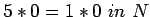 .
.
Some atomic propositions are proved by computation on terms and
proofs. For example,
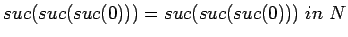 is
proved by thrice iterating the inference rule
is
proved by thrice iterating the inference rule 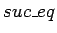
We might take the object
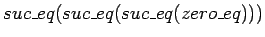 as a proof
expression for this equality. On the other hand, in such a case we can just
as well consider the proof to be a computation procedure on the terms whose
result is some token indicating success of the
procedure.
as a proof
expression for this equality. On the other hand, in such a case we can just
as well consider the proof to be a computation procedure on the terms whose
result is some token indicating success of the
procedure.
In general, the proofs of atomic propositions depends on an analysis of the
terms involved and the underlying type and its components. For example,
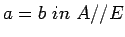 might involve a proof the proposition E(a,
b).
might involve a proof the proposition E(a,
b).
So we cannot say in advance what all the forms of proof are in these cases.
As a general guide, in the case of completely atomic propositions such as
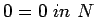 in which the terms and type are atomic, we speculate that the
proof is atomic as well. For these atomic proofs we might have a special
symbol such as axiom.26
in which the terms and type are atomic, we speculate that the
proof is atomic as well. For these atomic proofs we might have a special
symbol such as axiom.26
- 2.
- A proof of
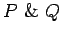 is a pair
is a pair
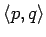 where p proves
P and q proves Q.
where p proves
P and q proves Q.
- 3.
- A proof of
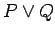 is either p or q where p proves P and q proves Q. To be more explicit we say it is a pair
is either p or q where p proves P and q proves Q. To be more explicit we say it is a pair
 where if the tag designates P then e is p and if it designates Q,
then e is q.
where if the tag designates P then e is p and if it designates Q,
then e is q.
- 4.
- A proof of
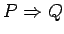 is a procedure f which maps any proof p of P to f(p), a proof of Q.
is a procedure f which maps any proof p of P to f(p), a proof of Q.
- 5.
- A proof of
![$\exists x\!:\!A.\ P[x]$](img521.gif) is a pair
is a pair
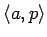 where
where
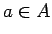 and p proves P[a].
and p proves P[a].
- 6.
- A proof of
![$\forall x\!:\!A.\ P[x]$](img523.gif) is a procedure f taking any element
a of A to a proof f(a) of P[a].
is a procedure f taking any element
a of A to a proof f(a) of P[a].
Note, we treat 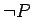 as
as
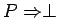 ,
so these definitions
give an account of negation, but there are other approaches,
such as
[12].
,
so these definitions
give an account of negation, but there are other approaches,
such as
[12].
We will see a finer analysis of this definition in the section on type
theory; there following [80] and
[109,110], we will distinguish between canonical proof
canonical proof expressions and non-canonical ones such as
add(suc(0); suc(suc(0))) (which reduces to a canonical one
suc(suc(suc(0)))). In this more refined analysis we say that the above
clauses define the canonical proofs, e.g. a canonical proof of 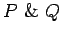 is a pair
is a pair
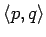 ,
but
,
but
 is a noncanonical
proof of
is a noncanonical
proof of 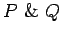 which reduces to
which reduces to
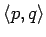 when we
``normalize'' the proof.
when we
``normalize'' the proof.
Although this is a suggestive semantics of both proofs and
propositions, several questions remain. Given a proposition P, can
we be sure that all proofs have the structure suggested by this
semantics? Suppose 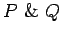 is not proved by proving P and proving
Q but instead by a case analysis or by decomposing an implication
and then decomposing an existential statement, etc.; so if t proves
is not proved by proving P and proving
Q but instead by a case analysis or by decomposing an implication
and then decomposing an existential statement, etc.; so if t proves
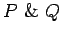 ,
do we know t is a pair?
,
do we know t is a pair?
If proofs are going to be objects, then what is the right equality relation on
them? If t proves 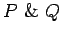 then is t at least equal to a pair
then is t at least equal to a pair
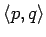 ? What is the right equality on propositions? If P=Qand p proves P does p prove Q? How can we make sense of Magic as a
proof object? It is a proof of
? What is the right equality on propositions? If P=Qand p proves P does p prove Q? How can we make sense of Magic as a
proof object? It is a proof of
 yet it has no structure of the
kind Heyting suggests. We will see that the type theories of the next
section provide just the right tools for answering these questions.
yet it has no structure of the
kind Heyting suggests. We will see that the type theories of the next
section provide just the right tools for answering these questions.



Next: Type theory
Up: Typed logic
Previous: Proofs as objects
James Wallis
1999-09-17
![]() .
.
![]() as
as
![]() ,
so these definitions
give an account of negation, but there are other approaches,
such as
[12].
,
so these definitions
give an account of negation, but there are other approaches,
such as
[12].
![]() is a pair
is a pair
![]() ,
but
,
but
![]() is a noncanonical
proof of
is a noncanonical
proof of ![]() which reduces to
which reduces to
![]() when we
``normalize'' the proof.
when we
``normalize'' the proof.
![]() is not proved by proving P and proving
Q but instead by a case analysis or by decomposing an implication
and then decomposing an existential statement, etc.; so if t proves
is not proved by proving P and proving
Q but instead by a case analysis or by decomposing an implication
and then decomposing an existential statement, etc.; so if t proves
![]() ,
do we know t is a pair?
,
do we know t is a pair?
![]() then is t at least equal to a pair
then is t at least equal to a pair
![]() ? What is the right equality on propositions? If P=Qand p proves P does p prove Q? How can we make sense of Magic as a
proof object? It is a proof of
? What is the right equality on propositions? If P=Qand p proves P does p prove Q? How can we make sense of Magic as a
proof object? It is a proof of
![]() yet it has no structure of the
kind Heyting suggests. We will see that the type theories of the next
section provide just the right tools for answering these questions.
yet it has no structure of the
kind Heyting suggests. We will see that the type theories of the next
section provide just the right tools for answering these questions.