CS 3410: Computer System Organization and Programming
Welcome to CS 3410 for fall 2024! Here are some useful links:
- The course schedule for lecture topics and all deadlines
- Please actually read the syllabus
- A schedule of office hours
- Ed, for Q&A
- Gradescope, where assignments and exams happen
- Canvas, which we are mostly not using but which will have some attendance tracking information
- Prof. Sampson’s lecture doodles
- Prof. Guidi’s slides
Syllabus
CS 3410, “Computer System Organization and Programming,” is your chance to learn how computers really work. You already have plenty of experience programming them at a high level, but how does your code in Java or Python translate into the actual operation of a chunk of silicon? We’ll cover systems programming in C, assembly programming in RISC-V, the architecture of microprocessors, the way programs interact with operating systems, and how to correctly and efficiently harness the power of parallelism.
In fall 2024, CS 3410 has a different structure! Compared to recent offerings of 3410, we’ll focus more on the software view of hardware and less on the digital logic foundations of machine architecture. There are also a larger number of small assignments instead of a few big projects. We appreciate your patience while we build this new approach to teaching computer systems!
TL;DR
- All course communication will happen on Ed.
- Log in with your
netid@cornell.eduemail address. You should already have access. - You’re responsible for knowing everything that we post as announcements there. Ignore announcements at your own risk.
- Log in with your
- Homework hand-in and grading happens on Gradescope.
- There are 11 assignments.
- The deadline is usually Wednesday night at 11:59pm. See the schedule for details.
- You have 12 total “slip days” you can use throughout the semester. You may use up to 3 for a given assignment.
- Your lowest homework score will be dropped.
- There is one prelim and a final exam.
Organization
Announcements and Q&A: Ed
We will be using Ed for all announcements and communication about the course. Log in there with your netid@cornell.edu email address. The course staff will post important updates there that you really want to know about! Check often, and don’t miss the announcement emails.
You can also ask questions—about lectures, homework, or anything else—on Ed.
What to post. If you can answer someone else’s question yourself, please do! But be careful not to post solutions. If you’re not sure whether something is OK to post, contact the course staff privately. You can do that by marking your question as “Private” when you post it.
How to ask a good question. A good post asks a specific question. Here are some examples of bad posts:
- “Tell me more about broad topic X.”
- “Does anyone have any hints for problem Y?”
If you need help with a homework problem, for example, be sure to include what you’ve tried already, exactly where you’re stuck, and what you’re currently thinking about how to proceed. If you just ask for help without any evidence of effort, we’ll punt the question back to you for more details.
Never post screenshots of code. They are inaccessible, hard to copy and paste, and hard to read on small screens (i.e., phones). Use Ed’s “code block” feature and paste the actual code.
Use Ed, not email. Do not contact individual TAs or the instructors via email. Use private Ed posts instead. The only exception is for sensitive topics that need to be kept confidential; please email cs3410-prof@cornell.edu (not the instructors’ personal addresses) with those.
Assignments: Gradescope
You will submit your solutions to assignments and receive grades through Gradescope.
We try to grade anonymously, i.e., the course staff won’t know who we’re grading. So please do not put your name or NetID anywhere in the files you upload to Gradescope. (Gradescope knows who you are!)
Content
Grading
Final grades will be assigned with these proportions:
- Assignments: 30%
- Preliminary Exam: 25%
- Final Exam: 25%
- Topic Mastery Quizzes: 10%
- Participation: 10%
Assignments
Problem sets are usually due on Wednesday at 11:59 PM. See the course schedule. All assignments are individual. You’ll turn in assignments via Gradescope.
Slip days. You have a total of 12 slip days to use throughout the semester, of which you can use at most 3 for a given assignment. A “slip day” is a 24-hour penalty-free extension on an assignment deadline that you can use without even asking for permission. Use slip days to make your life easier when dealing with:
- routine illness
- minor injury
- travel
- job fairs
- job interviews
- large workloads in other courses
- extra-curriculars
- just getting overwhelmed
We trust you to use your slip days wisely. They often mean you have less time to work on the next assignment.
Dropped score. We will drop one score to calculate your final grade: that is, your lowest-scoring problem set won’t count, even if that score is zero. Use this policy to cope with extenuating circumstances, or that especially difficult week in your semester, by skipping one assignment.
Other lateness. Late submissions (beyond slip days) will not be accepted. In truly exceptional circumstances where slip days do not cut it, contact the instructors. Exceptional circumstances require some accompanying documentation.
Grade cap. In terms of your final course grade, assignment scores are capped at 85%. All scores above 85% will count as “full credit” and an A average; scores below 85% will be scaled accordingly (e.g., 80% on an assignment maps to a final-grade value of 94.1%). This policy is meant to help you focus holistically on learning what each assignment is trying to teach you, not on maximizing individual points.
Exams
There is one preliminary exams and a final exam. See the course schedule.
Makeup exams must be scheduled within the first three weeks of class. Check the schedule now to see if you have a conflict with another class and use a private Ed post to reschedule.
Topic Mastery Quizzes
Weekly topic mastery quizzes will help reinforce the lessons from a given week’s lectures. We’ll release the quiz on Sunday. The material will be covered in lectures that week. The quiz due date is the following Friday. These quizzes are also on Gradescope.
Because they’re meant to help you practice, grading on these quizzes is very forgiving:
- You are welcome to retake the quiz as many times as you like. We’ll keep your best attempt.
- The score is capped at 90%, so scoring 9/10 is “full credit” and counts the same as scoring 10/10.
- We will drop your two lowest scores.
No extensions are available on these quizzes.
Labs
CS 3410 has lab sections that are designed to help you get started on assignments. Each assignment has a first step that you should be able to complete in lab, with lots of help from the TA. There is nothing separate to turn in for each lab—you’ll turn in your work as part of the associated assignment.
Attendance is required. You must attend the lab section you are registered for. (If you need to change lab sections, please use the “swap” feature on Student Center to avoid losing your spot in the main course registration.) You are responsible for making sure that your attendance is recorded each time.
Participation
The “participation” segment of your grade has three main components:
- 4% for Lecture attendance, as measured by occasional Poll Everywhere polls.
- 4% for lab attendance, as recorded by the lab’s instructors.
- 2% for surveys:
- The introduction survey (on Gradescope) in the first week of class.
- The mid-semester feedback survey.
- The semester-end course evaluation.
We know that life happens, so you can miss up to 3 lab sections and 5 lectures without penalty.
Policies
Academic Integrity
Absolute integrity is expected of all Cornell students in every academic undertaking. The course staff will prosecute violations aggressively.
You are responsible for understanding these policies:
- Cornell University Code of Academic Integrity
- Computer Science Department Code of Academic Integrity
On assignments, everything you turn in must be 100% completely your own work. You may discuss the work in generalities with other students using natural language, but you may not show anyone else your code or look at anyone else’s code. Specifically:
- Do not show any (partial or complete) solution to another student.
- Do not look at any (partial or complete) solution written by another student.
- Do not search the Internet for solutions, on Google or Stack Overflow or anywhere else.
- Do not post solutions on Ed, except in private threads with course staff.
- Do ask someone if you’re confused about what the assignment is asking for.
- Definitely ask the course staff if you’re not sure whether or not something is OK.
Here’s the policy for exams: you may not give assistance to anyone or receive assistance of any kind from anyone at all (outside of the course staff. All exams are closed book.
This course is participating in Accepting Responsibility (AR), which is a pilot supplement to the Cornell Code of Academic Integrity (AI). For details about the AR process and how it supplements the AI Code, see the AR website.
Generative AI
You may not use generative AI tools (e.g., ChatGPT, Gemini, or Copilot) to generate any code or text that you turn in. All work you submit must be 100% hand-written.
Respect in Class
Everyone—the instructors, TAs, and students—must be respectful of everyone else in this class. All communication, in class and online, will be held to a high standard for inclusiveness: it may never target individuals or groups for harassment, and it may not exclude specific groups. That includes everything from outright animosity to the subtle ways we phrase things and even our timing.
For example: do not talk over other people; don’t use male pronouns when you mean to refer to people of all genders; avoid explicit language that has a chance of seeming inappropriate to other people; and don’t let strong emotions get in the way of calm, scientific communication.
If any of the communication in this class doesn’t meet these standards, please don’t escalate it by responding in kind. Instead, contact the instructors as early as possible. If you don’t feel comfortable discussing something directly with the instructors—for example, if the instructor is the problem—please contact the CS advising office or the department chair.
Special Needs and Wellness
We provide accommodations for disabilities. Students with disabilities can contact Student Disability Services at for a confidential discussion of their individual needs.
If you experience personal or academic stress or need to talk to someone who can help, contact the instructors or:
- Engineering academic advising
- Arts & Sciences academic advising
- Learning Strategies Center
- Let’s Talk Drop-in Counseling at Cornell Health
- Empathy Assistance and Referral Service (EARS)
Please also explore other mental health resources available at Cornell.
Fall 2024 Course Schedule
Overview
| Week | Monday | Wednesday | Assignment | Lab |
|---|---|---|---|---|
| Aug 26 | 1+1=2 | Intro, C | printf | C Intro |
| Sep 2 | Labor Day | Float, Types | Minifloat | Float Practice |
| Sep 9 | Arrays & Pointers | Heap & Allocation | Huffman | Priority Queue |
| Sep 16 | Gates, Logic | State | Circuits | Logic Intro |
| Sep 23 | FemtoProc, CPU | ISAs, RISC-V | CPU Sim | Processors |
| Sep 30 | More RISC-V | Control Flow | Assembly | Assembly & Review |
| Oct 7 | Calling Conv. | Calling Conv. | Prelim | Assembly |
| Oct 14 | Fall Break | Caches | Functions | RISC-V Practice |
| Oct 21 | Caches | Caches | Blocking | Cache Intro |
| Oct 28 | Processes | System Calls | Shell | System Calls |
| Nov 4 | Virtual Memory | Threads | Optional | |
| Nov 11 | Atomics | Synchronization | Concurrent | LR/SC Practice |
| Nov 18 | Parallelism | Parallelism | Raycasting | Threads |
| Nov 25 | Parallelism | Thanksgiving | No Lab | |
| Dec 2 | Parallelism | Parallelism | Review | |
| Dec 9 | GPUs? |
Assignments
Assignments are usually due on Wednesday at 11:59pm. The table above shows the week when the assignment is assigned; it’s due during the next week (with some exceptions; see the bold dates). So the deadlines are:
- printf: Sep 4
- Minifloat: Sep 11
- Huffman Compression: Sep 18
- Generating Circuits: Sep 25
- CPU Simulation: Oct 2
- Assembly Programming: Oct 11 (before Fall Break)
- Functions in Assembly: Oct 23
- Cache Blocking: Oct 30
- Shell: Nov 13
- Concurrent Hash Table: Nov 20
- Parallel Raycasting: Dec 9 (last day of class)
Lab Sections
Lab sections are mostly on Thursday. One is on Wednesday and one is on Friday. The work in each lab is meant to help you get started on the assignment that is out that week; the Lab column above indicates the part of the assignment we’ll do together in section. There is nothing separate to turn in from lab; the work you do in lab will get turned in as part of that week’s assignment.
Exams
There are two exams:
- One preliminary exam, on October 8 at 7:30pm
- The final exam, on December 13 at 7pm
Office Hours
We look forward to seeing you in office hours! Check out the schedule of available office hours in this Google Calendar, which is also embedded below.
With TAs
TA office hours are either:
- In person, in Rhodes 529.
- On Zoom, using links associated with the events in the calendar.
In-person office hours use a simple whiteboard queueing mechanism; Zoom office hours use Queue Me In.
Office hours do not happen on official Cornell days off and breaks. (We will attempt to make the calendar reflect this fact, but please trust this statement over the calendar.)
With the Instructors
Instructor office hours are appropriate for discussing technical content and course logistics. They are less appropriate for getting help with a specific assignment; please see TAs for that.
- To book a session with Prof. Sampson, please find a time on this schedule.
- To book a session with Prof. Guidi, please find a time on this schedule.
Using the CS 3410 Infrastructure
The coursework for CS 3410 mainly consists of writing and testing programs in C and RISC-V assembly. You will need to use the course’s provided infrastructure to compile and run these programs.
Course Setup Video
We have provided a video tutorial detailing how to get started with the course infrastructure. Feel free to read the instructions below instead—they are identical to what the video describes.
Setting Up with Docker
This semester, you will use a Docker container that comes with all of the infrastructure you will need to run your programs.
The first step is to install Docker. Docker has instructions for installing it on Windows, macOS, and on various Linux distributions. Follow the instructions on those pages to get Docker up and running.
For Windows users: to type the commands in these pages, you can choose to use either the Windows Subsystem for Linux (WSL) or PowerShell. PowerShell comes built in, but you have to install WSL yourself. On the other hand, WSL lets your computer emulate a Unix environment, so you can use more commands as written. If you don’t have a preference, we recommend WSL.
Check your installation by opening your terminal and entering:
docker --version
Now, you’ll want to download the container we’ve set up. Enter this command:
docker pull ghcr.io/sampsyo/cs3410-infra
If you get an error like this: “Cannot connect to the Docker daemon at [path]. Is the docker daemon running?”, you need to ensure that the Docker desktop application is actively running on your machine. Start the application and leave it running in the background before proceeding.
This command will take a while. When it’s done, let’s make sure it works! First, create the world’s tiniest C program by copying and pasting this command into your terminal:
printf '#include <stdio.h>\nint main() { printf("hi!\\n"); }\n' > hi.c
(Or, you can just use a text editor and write a little C program yourself.)
Now, here are two commands that use the Docker container to compile and run your program.
docker run -i --rm -v ${PWD}:/root ghcr.io/sampsyo/cs3410-infra gcc hi.c
docker run -i --rm -v ${PWD}:/root ghcr.io/sampsyo/cs3410-infra qemu a.out
If your terminal prints “hi!” then you’re good to go!
You won’t need to learn Docker to do your work in this course. But to explain what’s going on here:
docker run [OPTIONS] ghcr.io/sampsyo/cs3410-infra [COMMAND]tells Docker to run a given command in the CS 3410 infrastructure container.- Docker’s
-ioption makes sure that the command is interactive, in case you need to interact with whatever’s going on inside the container, and--rmtells it not to keep around an “image” of the container after the command finishes (which we definitely don’t need). -v ${PWD}:/rootuses a Docker volume to give the container access to your files, likehi.c.
After all that, the important part is the actual command we’re running.
gcc hi.c compiles the C program (using GCC) to a RISC-V executable called a.out.
Then, qemu a.out runs that program (using QEMU).
Make an rv Alias
The Docker command above is a lot to type every time! To make this easier, we can use a shell alias.
On macOS, Linux, and WSL
Try copying and pasting this command:
alias rv='docker run -i --rm -v "$PWD":/root ghcr.io/sampsyo/cs3410-infra'
Now you can use much shorter commands to compile and run code.
Just put rv before the command you want to run, like this:
rv gcc hi.c
rv qemu a.out
Unfortunately, this alias will only last for your current terminal session.
To make it stick around when you open a new terminal window, you will need to add the alias rv=... command to your shell’s configuration file.
First type this command to find out which shell you’re using:
echo $SHELL
It’s probably bash or zsh, in which case you need to edit .bashrc or .zshrc in your home directory.
Here is a command you can copy and paste, but fill in the appropriate file according to your shell:
echo "alias rv='docker run -i --rm -v \"\$PWD\":/root ghcr.io/sampsyo/cs3410-infra'" >> ~/.bashrc
Change that ~/.bashrc at the end to ~/.zshrc if your shell is zsh.
On Windows with PowerShell (Not WSL)
(Remember, if you’re using WSL on Windows, please use the previous section.)
In PowerShell, we will create a shell function instead of an alias.
We assume that you have created a cs3410 directory on your computer where you’ll be storing all your code files.
First, open Windows PowerShell ISE (not the plain PowerShell) by typing it into the Windows search bar.
There will be an editor component at the top, right under Untitled1.ps1.
There, paste the following:
Function rv_d { docker run -i --rm -v ${PWD}:/root ghcr.io/sampsyo/cs3410-infra $args[0] $args[1] }
This will create a function called rv_d that takes two arguments (we’ll see what those are in a bit). We’re naming it rv_d and not just rv (as done in the next section) because PowerShell already has a definition for rv. The “d” stands for Docker.
Then, in the top left corner, click “File → Save As” and name your creation. Here, we’ll use function_rv_d. Finally, navigate to the cs3410 folder that stores all your work and once you’re there, hit “Save.”
Assuming you don’t delete it, that file will forever be there. This is how we put it to work:
Every time you’d like to run those long docker commands, open PowerShell (the plain one, not the ISE) and navigate to your cs3410 folder. Then, enter the following command:
. .\function_rv_d.ps1
This will run the code in that script file, therefore defining the rv_d function in your current PowerShell session. Then, navigate to wherever the .c file you’re working on is located (we assume it’s called file.c) and to compile it, simply type rv_d gcc file.c. Finally, to run the compiled code, enter rv_d qemu a.out. Try it out with your hi.c file.
Debugging C Code
GDB is an incredibly useful tool for debugging C code. It allows you to see where errors happen and step through your code one line at a time, with the ability to see values of variables along the way. Learning how to use GDB effectively will be very important to you in this course.
Entering GDB Commandline Mode
First, make sure to compile your source files with the -g flag. This flag will add debugging symbols to the executable that will allow GDB to debug much more effectively. For example, running:
rv gcc -g -Wall -Wextra -Wpedantic -Wshadow -Wformat=2 -std=c17 hi.c
In order to use gdb in the 3410 container, you need to open two terminals: one for running qemu with the debug mode in the background; and the other for invoking gdb and iteract with it.
- First, open a new terminal, and type the following commands:
docker run -i --rm -v `pwd`:/root --name cs3410 ghcr.io/sampsyo/cs3410-infra:latest. Feel free the change the “name” fromcs3410to any name you prefer.rv gcc -g -Wall ... (more flags) EXECUTABLE SOURCE.c. Once you have entered the container, compile your source file with the-gflag and any other recommended commands.qemu -g 1234 EXECUTABLE ARG1 ... (more arguments). Now you can start executingqemuwith the debug mode and invoke the executable fileEXECUTABLEwith any arguments you need to pass in.
- Then, open another terminal, and type the following commands:
docker exec -i cs3410 /bin/bash, wherecs3410is the placeholder for the name of the container you are running in the background via the first terminal.gdb --args EXECUTABLE ARG1 ... (more arguments)to start executing the GDB.target remote localhost:1234: execute this inside the GDB. It instructs GDB to perform remote debugging by connecting it to listen to the specified port.- Start debugging!
- Once you
quita GDB session, you need to go back to the first terminal to spin up theqemuagain (Step 1.3) and then invoke GDB again (Step 2.2 and onwards).
Checking for Common C Errors
Here are some important limitations of this method:
- You’ll have to run that script file every time you open a new PowerShell session.
- This function assumes you’ll only be using it to execute
rv_d gcc file.candrv_d qemu a.out(wherefile.canda.outare the.cfile and corresponding executable in question). For anything else, thisrv_dfunction doesn’t work. For those, you’d have to type in the entire Docker command and then whatever else after. Another incentive to go the WSL route.
Set Up Visual Studio Code
You can use any text editor you like in CS 3410. If you don’t know what to pick, many students like Visual Studio Code, which is affectionately known as VSCode.
It’s completely optional, but you might want to use VSCode’s code completion and diagnostics. Here are some suggestions:
- Install VSCode’s C/C++ extension. There is a guide to installing it in the docs.
- Configure VSCode to use the container. Put the contents of this file in
.devcontainer/devcontainer.jsoninside the directory where you’re doing your work for a given assignment. - Tell VSCode to use the RISC-V setup. Put the contents of this file in
.vscode/c_cpp_properties.jsonin your work directory.
Tools
This section contains some tutorial-level overviews of some tools you will use in CS 3410: SSH for remote login, the Unix shell and navigating the command line, and git for version control.
Unix Shell Tutorial
This is a modified version of Tutorials 1 and 2 of a Unix tutorial from the University of Surrey.
Listing Files and Directories
When you first open a terminal window, your current working directory is your home directory. To find out what files are in your home directory, type:
$ ls
(As with all examples in these pages, the $ is not part of the command.
It is meant to evoke the shell’s prompt, and you should type only the characters that come after it.)
There may be no files visible in your home directory, in which case you’ll just see another prompt.
By default, ls will skip some hidden files.
Hidden files are not special: they just have filenames that begin with a . character.
Hidden files usually contain configurations or other files meant to be read by programs instead of directly by humans.
To see everything, including the hidden files, use:
$ ls -a
ls is an example of a command which can take options, a.k.a. flags.
-a is an example of an option. The options change the behavior of the command. There are online manual pages that tell you which options a particular command can take, and how each option modifies the behavior of the command. (See later in this tutorial.)
Making Directories
We will now make a subdirectory in your home directory to hold the files you will be creating and using in the course of this tutorial. To make a subdirectory called “unixstuff” in your current working directory type:
$ mkdir unixstuff
To see the directory you have just created, type:
$ ls
Changing Directories
The command cd [directory] changes the current working directory to [directory].
The current working directory may be thought of as the directory you are in, i.e., your current position in the file-system tree.
To change to the directory you have just made, type:
$ cd unixstuff
Type ls to see the contents (which should be empty).
Exercise.
Make another directory inside unixstuff called backups.
The directories . and ..
Still in the unixstuff directory, type
$ ls -a
As you can see, in the unixstuff directory (and in all other directories), there are two special directories called . and ...
In UNIX, . means the current directory, so typing:
$ cd .
(with is a space between cd and .) means stay where you are (the unixstuff directory). This may not seem very useful at first, but using . as the name of the current directory will save a lot of typing, as we shall see later in the tutorial.
In UNIX, .. means the parent directory. So typing:
$ cd ..
will take you one directory up the hierarchy (back to your home directory). Try it now!
Typing cd with no argument always returns you to your home directory. This is very useful if you are lost in the file system.
Pathnames
Pathnames enable you to work out where you are in relation to the whole file-system. For example, to find out the absolute pathname of your home-directory, type cd to get back to your home-directory and then type:
$ pwd
pwd means “print working directory”. The full pathname will look something like this:
/home/youruser/unixstuff
which means that unixstuff is inside youruser (your home directory), which is in turn in a directory called home, which is in the “root” top-level directory, called /.
Exercise.
Use the commands ls, cd, and pwd to explore the file system.
Understanding Pathnames
First, type cd to get back to your home-directory, then type
$ ls unixstuff
to list the conents of your unixstuff directory.
Now type
$ ls backups
You will get a message like this -
backups: No such file or directory
The reason is, backups is not in your current working directory. To use a command on a file (or directory) not in the current working directory (the directory you are currently in), you must either cd to the correct directory, or specify its full pathname. To list the contents of your backups directory, you must type
$ ls unixstuff/backups
You can refer to your home directory with the tilde ~ character. It can be used to specify paths starting at your home directory. So typing
$ ls ~/unixstuff
will list the contents of your unixstuff directory, no matter where you currently are in the file system.
Summary
| Command | Meaning |
|---|---|
ls | list files and directories |
ls -a | list all files and directories |
mkdir | make a directory |
cd directory | change to named directory |
cd | change to home directory |
cd ~ | change to home directory |
cd .. | change to parent directory |
pwd | display the path of the current directory |
Copying Files
cp [file1] [file2] makes a copy of file1 in the current working directory and calls it file2.
We will now download a file from the Web so we can copy it around.
First, cd to your unixstuff directory:
$ cd ~/unixstuff
Then, type:
$ curl -O https://www.cs.cornell.edu/robots.txt
The curl command puts this text file into a new file called robots.txt.
Now type cp robots.txt robots.bak to create a copy.
Moving Files
mv [file1] [file2] moves (or renames) file1 to file2.
To move a file from one place to another, use the mv command. This has the effect of moving rather than copying the file, so you end up with only one file rather than two. It can also be used to rename a file, by moving the file to the same directory, but giving it a different name.
We are now going to move the file robots.bak to your backup directory.
First, change directories to your unixstuff directory (can you remember how?). Then, inside the unixstuff directory, type:
$ mv robots.bak backups/robots.bak
Type ls and ls backups to see if it has worked.
Removing files and directories
To delete (remove) a file, use the rm command. As an example, we are going to create a copy of the robots.txt file then delete it.
Inside your unixstuff directory, type:
$ cp robots.txt tempfile.txt
$ ls
$ rm tempfile.txt
$ ls
You can use the rmdir command to remove a directory (make sure it is empty first). Try to remove the backups directory. You will not be able to since UNIX will not let you remove a non-empty directory.
Exercise.
Create a directory called tempstuff using mkdir , then remove it using the rmdir command.
Displaying the contents of a file on the screen
Before you start the next section, you may like to clear the terminal window of the previous commands so the output of the following commands can be clearly understood. At the prompt, type:
$ clear
This will clear all text and leave you with the $ prompt at the top of the window.
The command cat can be used to display the contents of a file on the screen. Type:
$ cat robots.txt
As you can see, the file is longer than than the size of the window, so it scrolls past making it unreadable.
The command less writes the contents of a file onto the screen a page at a time. Type:
$ less robots.txt
Press the [space-bar] if you want to see another page, and type [q] if you want to quit reading.
The head command writes the first ten lines of a file to the screen.
First clear the screen, then type:
$ head robots.txt
Then type:
$ head -5 robots.txt
What difference did the -5 do to the head command?
The tail command writes the last ten lines of a file to the screen. Clear the
screen and type:
$ tail robots.txt
Exercise. How can you view the last 15 lines of the file?
Searching the Contents of a File
Using less, you can search though a text file for a keyword (pattern). For example, to search through robots.txt for the word “jpeg”, type
$ less robots.txt
then, still in less, type a forward slash [/] followed by the word to search
/jpeg
As you can see, less finds and highlights the keyword. Type [n] to search for the next occurrence of the word.
grep is one of many standard UNIX utilities. It searches files for specified words or patterns. First clear the screen, then type:
$ grep jpeg robots.txt
As you can see, grep has printed out each line containing the word “jpeg”.
To search for a phrase or pattern, you must enclose it in single quotes (the apostrophe symbol). For example to search for spinning top, type
$ grep 'web crawlers' robots.txt
Some of the other options of grep are:
-v: display those lines that do NOT match-n: precede each matching line with the line number-c: print only the total count of matched lines
Summary
| Command | Meaning |
|---|---|
cp file1 file2 | copy file1 and call it file2 |
mv file1 file2 | move or rename file1 to file2 |
rm file | remove a file |
rmdir directory | remove a directory |
cat file | display a file |
less file | display a file a page at a time |
head file | display the first few lines of a file |
tail file | display the last few lines of a file |
grep 'keyword' file | search a file for keywords |
Don’t stop here! We highly recommend completing the online UNIX tutorial, beginning with Tutorial 3.
Manual Pages
Unix has a built-in “help system” for showing documentation about commands, called man.
Try typing this:
$ man grep
That command launches less to read more than you ever wanted to know about the grep command.
If you want to know how to use a given command, try man <that_command>.
Saving Time on the Command Line
Tab completion is an extremely handy service available on the command line.
It can save you time and frustration by avoiding retyping filenames all the time.
Say you want to run this command to find all the occurrences of “gif” in robots.txt:
$ grep gif robots.txt
Try just typing part of the command first:
$ grep gif ro
Then hit the [tab] key.
Your shell should complete the name of the robots.txt file.
History
Type history at the command line to see your command history.
$ history
The Up Arrow
Use the up arrow on the command line instead of re-typing your most recent command. Want the command before that? Type the up arrow again!
Try it out! Hit the up arrow! If you’ve been stepping through these tips, you’ll probably see the command history.
Ctrl+r
If you need to find a command you typed 10 commands ago, instead of typing the up arrow 10 times, hold the [control] key and type [r]. Then, type a few characters contained within the command you’re looking for. Ctrl+r will reverse search your history for the most recent command that has that string.
Try it out! Assuming you’ve been working your way through all these tutorials,
typing Ctrl+r and then grep will show you your last grep command.
Hit return to execute that command again.
Git
Git is an extremely popular tool for software version control. Its primary purpose is to track your work, ensuring that as you make incremental changes to files, you will always be able to revert to, see, and combine old versions. When combined with a remote repository (in our case GitHub), it also ensures that you have an online backup of your work. Git is also a very effective way for multiple people to work together: collaborators can upload their work to a shared repository. (It certainly beats emailing versions back and forth.)
In CS 3410, we will use git as a way of disseminating assignment files to students and as a way for you to transfer, store, and backup your work. Please work in the class git repository that is created for you and not a repository of your own. (Publishing your code to a public repository is a violation of academic integrity rules.)
A good place to start when learning git is the free Pro Git book. This reference page will provide only a very basic intro to the most essential features of git.
Installing Git
If you do not have git installed on your own laptop, you can install it from the official website. If you encounter any problems, ask a TA.
Activate your Cornell GitHub Account
Before we can create a repository for you in this class, we will need you to activate your Cornell github account. Go to https://github.coecis.cornell.edu and log in with your Cornell NetID and password.
Create a Repository
Create a new repository on GitHub: Go to the top right of the GitHub home page, where you’ll see a bell, a plus sign, and your profile icon (which is likely just a pixely patterned square unless you uploaded your own). Click on the downward pointing triangle to the right of the plus sign, and you’ll see a drop-down menu that looks like this:
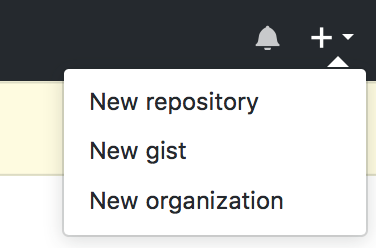
Click on “New repository” and then create a new repository like this:
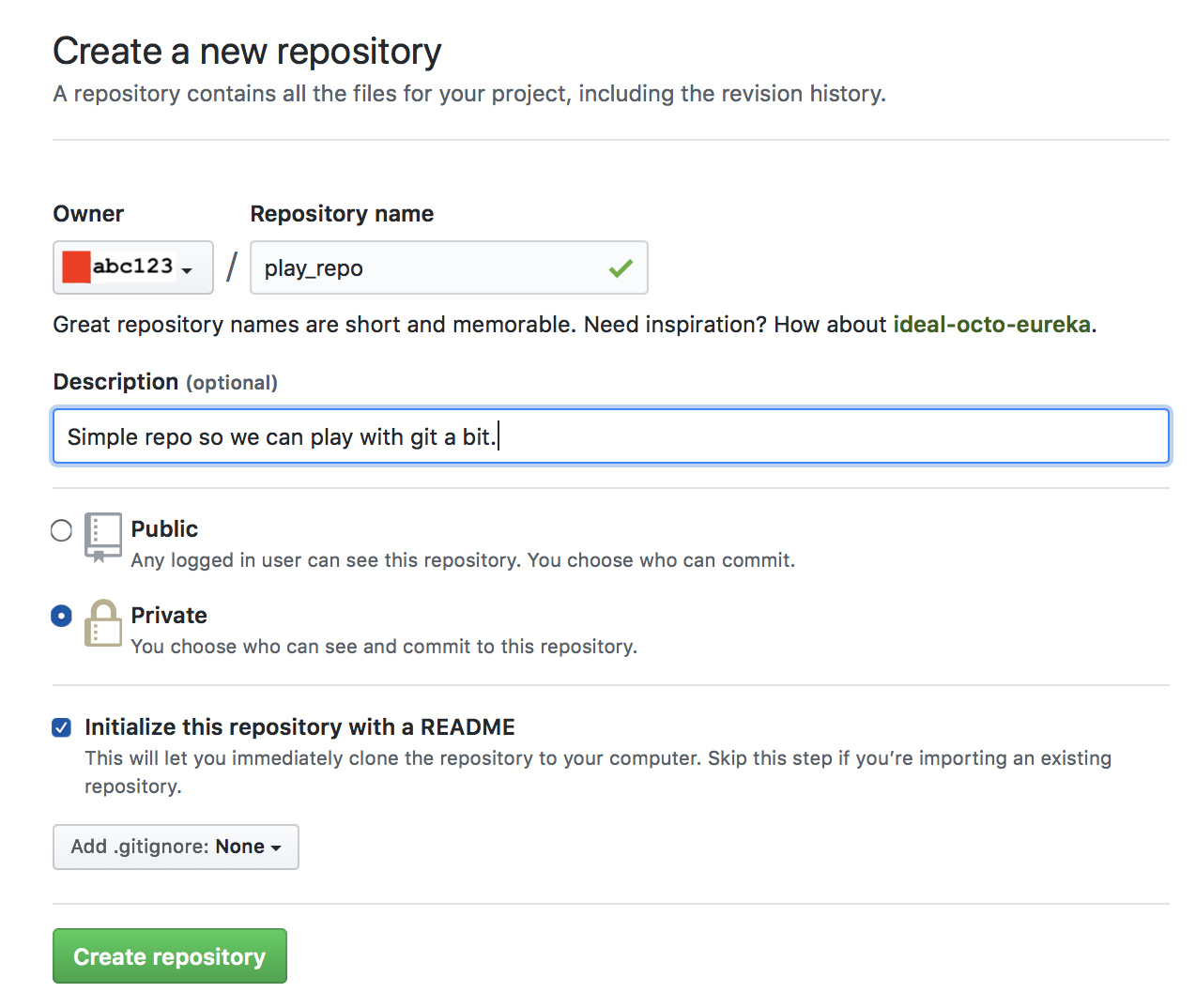
Note that the default setting is to make your repository public (visible to everyone). Any repository that contains code for this course should be made private; a public repository shares your code with others which constitutes an academic integrity violation.
Now click on the green “Create Repository” button.
Set Up Credentials
Before you can clone your repository (get a local copy to work on), you will need to set up SSH credentials with GitHub.
First, generate an SSH key if you don’t already have one. Just type this command:
$ ssh-keygen -C "<netid>@cornell.edu"
and use your NetID. The prompts will let you protect your key with a passphrase if you want.
Next, follow the instructions from GitHub to add the new SSH key to your GitHub account.
To summarize, go to Settings -> SSH and GPG Keys -> New SSH key,
and then paste the contents of a file named something like ~/.ssh/id_rsa.pub.
Clone the Repository
Cloning a git repository means that you create a local copy of its contents. You should clone the repository onto your own local machine (lab computer or laptop).
Find the green button on the right side of the GitHub webpage for your repository that says “Code”. Click it, then choose the “SSH” tab. Copy the URL there, which will look like this:
git@github.coecis.cornell.edu:abc123/play_repo.git
In a terminal, navigate to the folder where you would like to put your repository, and type:
$ git clone <PASTE>
That is, just type git clone (then a space) and paste the URL from GitHub.
Run this command to download the repository from GitHub to your computer.
At this point, you’ll get authentication errors if your SSH key isn’t set up correctly. So try that again if you get messages like “Please make sure you have the correct access rights and the repository exists.”
Look Around
Type cd play_repo to enter the repository. Type ls and you’ll see that your repo currently has just one file in it called README.md.
Type git status to see an overview of your repository. This command will show the status of your repository and the files that you have changed. At first, this command won’t show much.
Tracking Files with Git
There are 3 steps to track a file with git and send it to GitHub: stage, commit, and push.
Stage
To try it out, let’s make a new file.
Create a new file called <netid>.txt (use your NetID in there).
Now type git add NetID.txt from the directory containing the file to stage the file.
Staging informs git of the existence of the file so it can track its changes.
Type git status again.
You will see the file you added highlighted in green.
This means that the file is staged, but we still have two more steps to go to send your changes to GitHub.
(You might consider going back to the GitHub web interface to confirm that your new <netid>.txt file doesn’t show up there yet.)
Commit
A commit is a record of the state of the repository at a specific time. To make a commit, run this command:
$ git commit -m "Added my favorite color!"
The message after -m is a commit message, which is an explanation of the changes that you have made since you last committed. Good commit messages help you keep track of the work you’ve done.
This commit is now on your local computer. Try refreshing the GitHub repository page to confirm that it’s still not on the remote repository.
Push
To send our changes to the server, type this:
$ git push
The git push command sends any commits you have on your local machine to the remote machine.
You should imagine you are pushing them over the internet to GitHub’s servers.
Try refreshing the GitHub repository page again—now you should see your file there!
Pull
You will also want to retrieve changes from the remote server. This is especially helpful if you work on the repository from different machines. Type this command:
$ git pull
For now, this should just say that everything’s up to date. But if there were any new changes on the server, this would download them.
Typical Usage Pattern
Here is a good git workflow you should follow:
git pull: Type this before you start working to make sure you’re working on the most up to date version of your code (also in case the staff had to push any updates to you).- Work on your files.
git add file.txt: Type this for each file you either modified or added to the repo while you were working. Not sure what you touched or what’s new? Typegit statusand git will tell you!git commit -m "very helpful commit message": Save your changes in a commit. Write a message to remind your future self what you did.git push: Remember that, without the push, the changes are only your machine. If your laptop falls in a lake, then they’re gone forever. Push them to the server for safekeeping.
Git can be a little overwhelming, and sometimes the error messages can be hard to understand. Most of the time, following the instructions git gives you will help; if you run into real trouble, though, please ask a TA. If things get really messed up, don’t be afraid to clone a new copy of your repository and go from there.
It is completely OK to only know a few of the most common git commands and to not really understand how the whole thing works.
Many professional programmers get immense value out of git while only ever using add, commit, push, and pull.
Don’t worry about learning everything about git up front—you are already ready to use it productively!
Even More Commands
Here are a few other commands you might find useful. This is far from everything—there is a lot more in the git documentation.
Log
Type this command:
$ git log <netid>.txt
You’ll see the history of README.md.
You will see the author, time, and commit message for every commit of this file, along with the commit hash, which is how Git labels your commits and how you reference them if you need to.
At this point, you’ll only see a single commit.
But if you were to change the file and run git commit again, you would see the new change in the log.
You can also type git log with no filename afterward to get a history of all commits in your entire repository.
Stash
If you want to revert to the state of the last commit after making some new changes, you can type git stash.
Stashed changes are retrievable, but it might be a hassle to do so.
git stash only works on changes that have not yet been committed.
If you accidentally commit a change and want to wipe it out before pulling work from other machines, use git reset HEAD~1 to undo the last commit (and then stash).
Introduction to SSH
SSH (Secure SHell) is a tool that lets you connect to another computer over the Internet to run commands on it.
You run the ssh command in your terminal to use it.
The Cornell CS department has several machines available to you, if you want to use them to do your work. SSH is the (only) way to connect to these machines.
Accessing Cornell Resources from Off Campus
Cornell’s network requires you to be on campus to connect to Cornell machines. (This is a security measure: it is meant to prevents attacks from off campus.)
To access Cornell machines when you’re elsewhere, Cornell provides a mechanism called a Virtual Private Network (VPN) that lets you pretend to be on campus. Read more about Cornell’s VPN if you need it.
Log On
Make sure you are connected to the VPN or Cornell’s WiFi. Open a terminal window and type:
ssh <netid>@ugclinux.cs.cornell.edu
but replace <>).
Type yes and hit enter to accept the new SSH host key.
Now type your NetID password.
You’re in! You should see a shell prompt; you can follow the Unix shell tutorial to learn how to use it.
Here, ugclinux.cs.cornell.edu is the name of a collection of servers that Cornell runs for this purpose.
That’s what you’d replace with a different domain name to connect to a different machine.
scp
Suppose you have a file on the ugclinux machines and you want to get a copy locally onto your machine.
The scp command can do this.
It works like a super-powered version of the cp command that can copy between machines.
Say your file game.c is located at /home/yourNetID/mygame/game.c on ugclinux.
On your local machine (i.e., when not connected over SSH already), type:
$ scp yourNetID@ugclinux.cs.cornell.edu:mygame/game.c .
Here are the parts of that command:
$ scp <user>@<host>:<source> <dest>
<user> and <host> are the same information you use to connect to the remote machine with the ssh command.
<source> is the file on that remote machine that you want to obtain,
and <dest> is the place where you want to copy that file to.
Makefile Basics
This document is meant to serve as a very brief reference on how to read the Makefiles provided in this class. This tutorial is meant to be just enough to help you read the Makefiles you provide, and is not meant to be a complete overview of Makefiles or enough to help you make your own. If you are interested in learning more, there are some good tutorials online, such as this walkthrough.
A Makefile is often used with C to help with automating the (repetitive) task of compiling multiple files. This is especially helpful in cases where there are multiple pieces of your codebase you want to compile separately, such as choosing to test a program or run that program.
Variables
To illustrate how this works, let us examine a few lines in the Makefile that will be used for the minifloat assignment. Our first line of code is to define a variable CFLAGS:
CFLAGS=-Wall -Wpedantic -Werror -Wshadow -Wformat=2 -Wconversion -std=c99
As in other settings, defining this variable CFLAGS allows us to use the contents (a string in this case) later in our Makefile. Our specific choice of CFLAGS here is to indicate that we are defining the flags (for C) that we will be using in this Makefile. Later, when we use this variable in-line, the Makefile will simply replace the variable with whatever we defined it as, thus allowing us to use the same flags consistently for every command we run.
Commands
The rest of our Makefile for this assignment will consist of commands. A command has the following structure:
name: dependent_files
operation_to_run
The name of a command is what you run in your terminal after make, such as make part1 or make all (this gets a bit more complicated in some cases). The dependent_files indicate which files this command depends on – the Makefile will only run this command if one of these files changed since the last time we ran it. Finally, the operation is what actually gets run in our console, such as when we run gcc main.c -o main.o.
Example Command
To make this more concrete, let us examine our first command for part1:
part1: minifloat.c minifloat_test_part1.c minifloat_test_part1.expected
$(CC) $(CFLAGS) minifloat.c minifloat_test_part1.c -o minifloat_test_part1.out
This command will execute when we run make part1, but only if one of minifloat.c, minifloat_test_part1.c or minifloat_test_part1.expected have been modified since we last ran this command. What actually runs is the next line, with the $(CC), $(CFLAGS), and a bunch of filenames. $(CC) is a standard Makefile variable that is replaced by our C compiler – in our case, this is gcc. The $(CFLAGS) variable here is what we defined earlier, so we include all of the flags we desired. Finally, the list of files is exactly the same as we might normally run with gcc. In total, then, this entire operation will be translated to:
$(CC) $(CFLAGS) minifloat.c minifloat_test_part1.c -o minifloat_test_part1.out
-->
gcc $(CFLAGS) minifloat.c minifloat_test_part1.c -o minifloat_test_part1.out
-->
gcc -Wall -Wpedantic -Werror -Wshadow -Wformat=2 -Wconversion -std=c99 minifloat.c minifloat_test_part1.c -o minifloat_test_part1.out
This compilation would be a huge pain to type out everytime, especially with all of those flags (and easy to mess up), but with the Makefile, we can run all this with just make part1. We can do the same with make part2 to run the next set of commands instead.
Clean
One final node is that it is conventional (though not required) to include a make clean that removes any generated files, often for being able to clean up our folder or push our work to a Git repository. In our particular file, we have defined clean to remove the generated .out files and any .txt files that were used for testing:
clean:
rm -f *.out.stackdump
rm -f *.out
rm -f *.txt
Complete Makefile
For reference, the entirity of our Makefile is included here:
CFLAGS=-Wall -Wpedantic -Werror -Wshadow -Wformat=2 -Wconversion -std=c99
CC = gcc
all: part1 part2 part3
part1: minifloat.c minifloat_test_part1.c minifloat_test_part1.expected
$(CC) $(CFLAGS) minifloat.c minifloat_test_part1.c -o minifloat_test_part1.out
part2: minifloat.c minifloat_test_part2.c
$(CC) $(CFLAGS) minifloat.c minifloat_test_part2.c -o minifloat_test_part2.out
part3: minifloat.c minifloat_test_part3.c
$(CC) $(CFLAGS) minifloat.c minifloat_test_part3.c -o minifloat_test_part3.out
clean:
rm -f *.out.stackdump
rm -f *.out
rm -f *.txt
.PHONY: all clean
C Programming
Much of the work in CS 3410 involves programming in C. This section of the site contains some overviews of most of the C features you will need in CS 3410.
For authoritative details on C and its standard library,
the C reference on cppreference.com (despite the name) is a good place to look.
For example, here’s a list of all the functions in the stdio.h header, and here’s the documentation specifically about the fputs function.
Compiling and Running C Code
Before you proceed with this page, follow the instructions to set up the course’s RISC-V infrastructure.
Your First C Program
Copy and paste this program into a text file called first.c:
#include <stdio.h>
int main() {
printf("Hello, CS 3410!\n");
return 0;
}
Next, run this command:
$ rv gcc -o first first.c
Here are some things to keep in mind whenever these pages ask you to run a command:
- The
$is not part of the command. This is meant to evoke the command-line prompt in many shells, and it is there to indicate to you that the text that follows is a command that you should run. Do not include the$when you type the command. - Our course’s RISC-V infrastructure setup has you create an
rvalias for running commands inside the infrastructure container. We will not always include anrvprefix on example commands we list in these pages. Whenever you need to run a tool that comes from the container, use thervprefix or some other mechanism to make sure the command runs in the container. - As with all shell commands, it really matters which directory you’re currently “standing in,” called the working directory. Here,
first.candfirstare both filenames that implicitly refer to files within the working directory. So before running this command, be sure tocdto the place where yourfirst.cfile exists.
If everything worked, you can now run this program with this command:
$ rv qemu first
Hello, CS 3410!
(Just type the rv qemu first part. The next line, without the $, is meant to show you what the command should print as output after you hit return.)
This command uses QEMU, an emulator for the RISC-V instruction set, to run the program we just compiled, which is in the file named first.
Recommended Options
While the simple command gcc -o first first.c works fine for this simple example, we officially recommend that you always use a few additional command-line options that make the GCC compiler more helpful.
Here are the ones we recommend:
-Wall -Wextra -Wpedantic -Wshadow -Wformat=2 -std=c17
In other words, here’s our complete recommended command for compiling your C code:
$ rv gcc -Wall -Wextra -Wpedantic -Wshadow -Wformat=2 -std=c17 hi.c
Many assignments will include a Makefile that supplies these options for you.
Checking for Common C Errors
Memory-related bugs in C programs are extremely common! The worst thing about them is that they can cause obscure problems silently, without even crashing with a reasonable error message. Fortunately, GCC has built-in tools called sanitizers that can (much of the time, but not always) catch these bugs and give you reasonable error messages.
To use the sanitizers, add these flags to your compiler command:
-g -fsanitize=address -fsanitize=undefined
So here’s a complete compiler command with sanitizers enabled:
$ rv gcc -Wall -Wextra -Wpedantic -Wshadow -Wformat=2 -std=c17 -g -fsanitize=address -fsanitize=undefined hi.c
Then run the resulting program to check for errors.
We recommend trying the sanitizers whenever your code does something mysterious or unpredictable. It’s an unfortunate fact of life that, unlike many other languages, bugs in C code can silently cause weird behavior; sanitizers can help counteract this deeply frustrating problem.
C Basics
This section is an overview of the basic constructs in any C program.
Variable Declarations
C is a statically typed languages, so when you declare a variable, you must also declare its type.
int x;
int y;
Variable declarations contain the type (int in this example) and the variable name (x and y in this example).
Like every statement in C, they end with a semicolon.
Assignment
Use = to assign new values to variables:
int x;
x = 4;
As a shorthand, you can also include the assignment in the same statement as the declaration:
int y = 6;
Expressions
An expression is a part of the code that evaluates to a value, like 10 or 7 * (4 + 2) or 3 - x.
Expressions appear in many places, including on the right-hand side of an = in an assignment.
Here are a few examples:
int x;
x = 4 + 3 * 2;
int y = x - 6;
x = x * y;
Functions
To define a function, you need to write these things, in order: the return type, the function name, the parameter list (each with a type and a name), and then the body. The syntax looks like this:
<return type> <name>(<parameter type> <parameter name>, ...) {
<body>
}
Here’s an example:
int myfunc(int x, int y) {
int z = x - 2 * y;
return z * x;
}
Function calls look like many other languages:
you write the function name and then, in parentheses, the arguments.
For example, you can call the function above using an expression like myfunc(10, 4).
The main Function
Complete programs must have a main function, which is the first one that will get called when the program starts up.
main should always have a return type of int.
It can optionally have arguments for command-line arguments (covered later).
Here’s a complete program:
int myfunc(int x, int y) {
int z = x - 2 * y;
return z * x;
}
int main() {
int z = myfunc(1, 2);
return 0;
}
The return value for main is the program’s exit status.
As a convention, an exit status of 0 means “success” and any nonzero number means some kind of exceptional condition.
So, most of the time, use return 0 in your main.
Includes
To use functions declared somewhere else, including in the standard library, C uses include directives. They look like this:
#include <hello.h>
#include "goodbye.h"
In either form, we’re supplying the filename of a header file.
Header files contain declarations for functions and variables that C programs can use.
The standard filename extension for header files in C is .h.
You should use the angle-bracket version for library headers and the quotation-mark version for header files you write yourself.
Printing
To print output to the console, use printf, a function from the C standard library which takes:
- A string to print out, which may include format specifiers (more on these in a moment).
- For each format specifier, a value to fill in for each format specifier.
The first string might have no format specifiers at all, in which case the printf only has a single argument.
Here’s what that looks like:
#include <stdio.h>
int main() {
printf("Hello, world!\n");
}
The \n part is an escape sequence that indicates a newline, i.e., it makes sure the next thing we output goes on the next line.
Format specifiers start with a % sign and include a few more characters describing how to print each additional argument.
For example, %d prints a given argument as a decimal integer.
Here’s an example:
#include <stdio.h>
int main() {
int x = 3;
int y = 4;
printf("x + y = %d.\n", x + y);
}
Here are some format specifiers for printing integers in different bases:
| Base | Format Specifier | Example |
|---|---|---|
| decimal | %d | printf("%d", i); |
| hexadecimal | %x | printf("%x", i); |
| octal | %o | printf("%o", i); |
And here are some common format specifiers for other data types:
| Data Type | Format Specifier | Example |
|---|---|---|
string | %s | printf("%s", str); |
char | %c | printf("%c", c); |
float | %f | printf("%f", f); |
double | %lf | printf("%lf", d); |
long | %ld | printf("%ld", l); |
long long | %lld | printf("%lld", ll); |
| pointers | %p | printf("%p", ptr); |
See the C reference for details on the full set of available format specifiers.
Basic Types in C
Some Common Data Types
| Type | Common Size in Bytes | Interpretation |
|---|---|---|
char | 1 | one ASCII character |
int | 4 | signed integer |
float | 4 | single-precision floating-point number |
double | 8 | double-precision floating-point number |
A surprising quirk about C is that the sizes of some types can be different in different compilers and platforms! So this table lists common byte sizes for these types on popular platforms.
Characters
Every character is corresponds to a number. The mapping between characters and numbers is called the text encoding, and the ubiquitous one for basic characters in the English language is called ASCII. Here is a table with some of the most common characters in ASCII:

For all the characters in ASCII (and beyond), see this ASCII table.
Booleans
C does not have a bool data type available by default.
Instead, you need to include the stdbool.h header:
#include <stdbool.h>
That lets you use the bool type and the true and false expressions.
If you get an error like unknown type name 'bool', just add the include above to fix it.
Prototypes and Headers
Declare Before Use
In C, the order of declarations matters. This program with two functions works fine:
#include <stdio.h>
void greet(const char* name) {
printf("Hello, %s!\n", name);
}
int main() {
greet("Eva");
return 0;
}
But what happens if you just reverse the two function definitions?
#include <stdio.h>
int main() {
greet("Eva");
return 0;
}
void greet(const char* name) {
printf("Hello, %s!\n", name);
}
The compiler gives us this somewhat confusing error message:
error: implicit declaration of function 'greet'
The problem is that, in C,
you have to declare every name before you can use it.
So the declaration of greet has to come earlier in the file than the call to greet("Eva").
Declarations, a.k.a. Prototypes
This declare-before-use rule can make it awkward to define functions in the order you want, and it seems to be a big problem for mutual recursion. Fortunately, C has a mechanism to let you declare a name before you define what it means. All the functions we’ve seen so far have been definitions (a.k.a. implementations), because they include the body of the function. A function declaration (a.k.a. prototype) looks the same, except that we leave off the body and just write a semicolon instead:
void greet(const char* name);
A declaration like this tells the compiler the name and type of the function, and it amounts to a promise that you will later provide a complete definition.
Here’s a version of our program above that works and keeps the function definition order we want (main and then greet):
#include <stdio.h>
void greet(const char* name);
int main() {
greet("Eva");
return 0;
}
void greet(const char* name) {
printf("Hello, %s!\n", name);
}
By including the declaration at the top of the file, we are now free to call greet even though the definition comes later.
Header Files
It is so common to need to declare a bunch of functions so you can call them later that C has an entire mechanism to facilitate this:
header files.
A header is a C source-code file that contains declarations that are meant to be included in other C files.
You can then “copy and paste” the contents of header files into other C code using the #include directive.
Even though the C language makes no formal distinction between what you can do in headers and in other files, it is a universal convention that headers have the .h filename extension while “implementation” files use the .c extension.
For example, we could put our greet declaration into a utils.h header file:
void greet(const char* name);
Then, we might put this in main.c:
#include <stdio.h>
#include "utils.h"
int main() {
greet("Eva");
return 0;
}
void greet(const char* name) {
printf("Hello, %s!\n", name);
}
The line #include "utils.h" instructs the C preprocessor to look for the file called utils.h and paste its entire contents in at that location.
Because the preprocessor runs before the compiler, this two-file version of our project looks exactly the same to the compiler as if we had merged the two files by hand.
You can read more about #include directives, including about the distinction between angle brackets and quotation marks.
Multiple Source Files
Eventually, your C programs will grow large enough that it’s inconvenient to keep them in one .c file.
You could distribute the contents across several files and then #include them, but there is a better way:
we can compile source files separately and then link them.
To make this work in our example, we will have three files.
First, our header file utils.h, as before, just contains a declaration:
void greet(const char* name);
Next, we’re write an accompanying implementation file, utils.c:
#include <stdio.h>
#include "utils.h"
void greet(const char* name) {
printf("Hello, %s!\n", name);
}
As a convention, C programmers typically write their programs as pairs of files:
a header and an implementation file, with the same base name and different extensions (.h and .c).
The idea is that the header declares exactly the set of functions that the implementation file defines.
So in that way, the header file acts as a short “table of contents” for what exists in the longer implementation file.
Let’s call the final file main.c:
#include "utils.h"
int main() {
greet("Eva");
return 0;
}
Notably, we use #include "utils.h" to “paste in” the declaration of greet, but we don’t have its definition here.
Now, it’s time to compile the two source files, utils.c and main.c.
Here are the commands to do that:
$ gcc -c utils.c -o utils.o
$ gcc -c main.c -o main.o
(Remember to prefix these commands with rv to use our RISC-V infrastructure.)
The -c flag tells the C compiler to just compile the single source file into an object file, not an executable.
An object file contains all code for a single C source program, but it is not directly runnable yet—for one thing, it might not have a main function.
Using -o utils.o tells the compiler to put the output in a file called utils.o.
As a convention, the filename extension for object files is .o.
You’ll notice that we only compiled the .c files, not the .h files.
This is intentional: header files are only for #includeing into other files.
Only the actual implementation files get compiled.
Finally, we need to combine the two object files into an executable. This step is called linking. Here’s how to do that:
$ gcc utils.o main.o -o greeting
We supply the compiler with two object files as input and tell it where to put the resulting executable with -o greeting.
Now you can run the program:
$ ./greeting
(Use rv qemu greeting to use the course RISC-V infrastructure.)
Control Flow
Logical Operators
Here are some logical operators you can use in expressions:
| Expression | True If… |
|---|---|
expr1 == expr2 | expr1 is equal to expr2 |
expr1 != expr2 | expr1 is not equal to expr2 |
expr1 < expr2 | expr1 is less than expr2 |
expr1 <= expr2 | expr1 is less than or equal to expr2 |
expr1 > expr2 | expr1 is greater than expr2 |
expr1 >= expr2 | expr1 is greater than or equal to expr2 |
!expr | expr is false (i.e., zero) |
expr1 && expr2 | expr1 and expr2 are true |
expr1 || expr2 | expr1 or expr2 is true |
false && expr2 will always evaluate to false, and true || expr2 will always evaluate to true, regardless of what expr2 evaluates to.
This is called “short circuiting”: C evaluates the left-hand side of these expressions first and, if the truth value of that expression means that the other one doesn’t matter, it won’t evaluate the right-hand side at all.
Conditionals
Here is the syntax for if/else conditions:
if (condition) {
// code to execute if condition is true
} else if (another_condition) {
// code to execute if condition is false but another_condition is true
} else {
// code to execute otherwise
}
The else if and else parts are optional.
Switch/Case
A switch statement can be a succinct alternative to a cascade of if/elses when you are checking several possibilities for one expression.
switch (expression) {
case constant1:
// code to execute if expression equals constant1
break;
case constant2:
// code to execute if expression equals constant2
break;
// ...
default:
// code to be executed if expression doesn't match any case
}
While Loop
while (condition) {
// code to execute as long as condition is true
}
For Loop
for (initialization; condition; increment) {
// code to execute for each iteration
}
Roughly speaking, this for loop behaves the same way as this while equivalent:
initialization;
while (condition) {
// code to execute for each iteration
increment;
}
break and continue
To exit a loop early, use a break; statement.
A break statement jumps out of the innermost enclosing loop or switch statement.
If the break statement is inside nested contexts, then it exits only the most immediately enclosing one.
To skip the rest of a single iteration of a loop, but not cancel the loop entirely, use continue.
Declaring Your Own Types in C
Structures
The struct keyword lets you declare a type that bundles together several values, possibly of different types.
To access the fields inside a struct variable, use dot syntax, like thing.field.
Here’s an example:
struct rect_t {
int left;
int bottom;
int right;
int top;
};
int main() {
struct rect_t myRect;
myRect.left = -4;
myRect.bottom = 1;
myRect.right = 8;
myRect.top = 6;
printf("Bottom left = (%d,%d)\n", myRect.left, myRect.bottom);
printf("Top right = (%d,%d)\n", myRect.right, myRect.top);
return 0;
}
This program declares a type struct rect_t and then uses a variable myRect of that type.
Enumerations
The enum keyword declares a type that can be one of several options.
Here’s an example:
enum threat_level_t {
LOW,
GUARDED,
ELEVATED,
HIGH,
SEVERE
};
void printOneLevel(enum threat_level_t threat) {
switch (threat) {
case LOW:
printf("Green/Low.\n");
break;
// ...omitted for brevity...
case SEVERE:
printf("Red/Severe.\n");
break;
}
}
void printLevels() {
printf("Threat levels are:\n");
for (int i = LOW; i <= SEVERE; i++) {
printOneLevel(i);
}
}
This code declares a type enum threat_level_t that can be one of 5 values.
Type Aliases
You can use the typedef keyword to give new names to existing types.
Use typedef <old type> <new name>;, like this:
typedef int whole_number;
Now, you can use whole_number to mean the same thing as int.
Short Names for Structs and Enums
You may have noticed that struct and enum declarations make types that are kind of long and hard to type.
For example, we declared a type enum threat_level_t.
Wouldn’t it be nice if this type could just be called threat_level_t?
typedef is also useful for defining these short names.
You could do this:
enum _threat_level_t { ... }
typedef enum _threat_level_t threat_level_t;
And that does work! But there’s also a shorter way to do it, by combining the enum and the typedef together:
typedef enum {
...
} threat_level_t;
That defines an anonymous enumeration and then immediately gives it a sensible name with typedef.
Pointers!
Pointers are central to programming in C, yet are often one of the most foreign concepts to new C coders.
A Motivating Example
Suppose we want to write a swap function that will take two integers and swap their values. With the programming tools we have so far, our function might look something like this:
void swap(int a, int b) {
int temp = a;
a = b;
b = temp;
}
This won’t work how we want!
If we call swap(foo, bar), the swap function gets copies of the values in foo and bar.
Reassigning a and b just affects those copies—not foo and bar themselves!
How can we give swap direct access to the places where the arguments are stored so it can actually swap them?
Pointers are the answer.
Pointers are addresses in memory, and you can think of them as referring to a value that lives somewhere else.
Declaring a Pointer
For any type T, the type of a pointer to a value of that type is T*: that is, the same type with a star after it.
For example, this code:
char* my_char_pointer;
(pronounced “char star my char pointer”) declares a variable with the name my_char_pointer.
This variable is not a char itself!
Instead, it is a pointer to a char.
Confusingly, the spaces don’t matter. The following three lines of code are all equivalent declarations of a pointer to an integer:
int* ptr;
int *ptr;
int * ptr;
ptr has the type “pointer to an integer.”
Initializing a Pointer
int* ptr = NULL;
The line above initializes the pointer to NULL, or zero. It means the pointer does not point to anything. This is a good idea if you don’t plan on having it point to something just yet. Initializing to NULL helps you avoid “dangling” pointers which can point to random memory locations that you wouldn’t want to access unintentionally. C will not do this for you.
You can check if a pointer is NULL with the expression ptr == NULL.
Assigning to a Pointer, and Getting Addresses
In the case of a pointer, changing its value means changing where it points. For example:
void func(int* x) {
int* y = x;
// ...
The assignment in that code makes y and x point to the same place.
But what if you want to point to a variable that already exists?
C has an & operator, called the “address-of” operator, that gets the pointer to a variable.
For example:
int x = 5;
int* xPtr = &x;
Here, xPtr now points to x.
You can’t assign to the address of things; you can only use & in expressions (e.g., on the right-hand side of an assignment).
So:
y = &x; // this is fine
&x = y; // will not compile!
This rule reflects the fact that you can get the location of any variable, but it is never possible to change the location of a variable.
Dereferencing Pointers
Once you have a pointer with a memory location in it, you will want to access the value that is being pointed at—either reading or changing the value in the box at the end of the arrow.
For this, C has the * operator, known as the “dereferencing” operator because it follows a reference (pointer) and gives you the referred-to value.
You can both read from and write to a dereferenced pointer, so * expressions can appear on either side of an assignment.
For example:
int number = *xPtr; // read the value xPtr points to
printf("the number is %d\n", *xPtr); // read it and then print it
*xPtr = 6; // write the value that xPtr points to
Common Confusion with the * Operator
Do not be confused by the two contexts in which you will see the star (*) symbol:
- Declaring a pointer:
int* p; - Dereferencing a pointer (RHS):
r = *p; - Dereferencing a pointer (LHS):
*p = r;
The star is part of the type name when declaring a pointer and is the dereference operator when used in assignments.
Swap with Pointers
Now that we have pointers, we can correctly write that swap function we wanted! The new version of swap uses a “pass by reference” model in which pointers to arguments are passed to the function.
void swap(int* a, int* b) {
int temp = *a;
*a = *b;
*b = temp;
}
The Arrow Operator
Recall that we used the “dot” operator to access elements within a struct, like myRect.left.
If you instead have a pointer to a struct, you need to dereference it first before you can access its fields,
like (*myRect).left.
Fortunately, C has a shorthand for this case!
You can also write myRect->left to mean the same thing.
In other words, the -> operator works like the . operator except that it also dereferences the pointer on the left-hand side.
Pointer Arithmetic
If pointers are just addresses in memory, and addresses are just integers,
you might wonder if you can do arithmetic on them like you can with ints.
Yes, you can!
Adding n to a pointer to any type T causes the pointer to point n Ts further in memory.
For example, the expression ptr + offset might compute a pointer that is “four ints later in memory” or “six chars later in memory.”
int x = 5;
int *ptr = ...;
x = x + 1;
ptr = ptr + 1;
In this code:
x + 1: adds 1 to to the integerx, producing 6ptr + 1: adds the size of anintin bytes toptr, shifting to point to the next integer in memory
Printing Pointers
You can print the address of a pointer to see what memory location it is pointing to. For example:
printf("Pointer address: %p\n", (void*)ptr);
This will output the memory address the pointer ptr is currently holding.
Arrays
An array is a sequence of same-type values that are consecutive in memory.
Declaring an Array
To declare an array, specify its type and size (the number of items in the sequence). For example, an array of 4 integers can be declared as follows:
int myArray[4];
A few variations on this declaration are:
int myArray[4] = {42, 45, 65, -5}; // initializes the values in the array
int myArray[4] = {0}; // initializes all the values in the array to 0
int myArray[] = {42, 45, 65, -5}; // initializes the values in the array, compiler intuits the array size
Accessing an Array
To refer to an element, one must specify the array name (for example, my_array) and the position number (for example, 0):
int my_array[5];
my_array[0] = 8;
printf("I just initialized the element at index 0 to %d!\n", my_array[0]);
After which the array would look like this in memory (where larger addresses are higher on the screen):

To sum the elements of an array, we might write code like this:
int sum_array(int *array, int n) {
int sum = 0;
for (int i = 0; i < n; ++i) {
answer += array[i];
}
return sum;
}
int main() {
int data[4] = {4, 6, 3, 8};
int sum = sum_array(data, 4);
printf("sum: %d\n", sum);
return 0;
}
Accessing an Array using Pointer Arithmetic
In C, you can treat arrays as pointers: namely, to the first element in the sequence.
This means that, perhaps surprisingly, the syntax array[i] is shorthand for *(array + i):
that is, a combination of pointer arithmetic and dereferencing.
So you can think of array[i] as treating array as a pointer to the first element, then shifting the pointer over by i slots, and then dereferencing the pointer to that shifted location.
Passing Arrays as Parameters
You can also treat arrays as pointers when you pass them into functions. You already saw this above; we declared a function this way:
int sum_array(int *array, int n) { ... }
and then called it like sum_array(data, 4).
Even though we declared data as an array, C lets you treat it as a pointer to the first element.
It’s usually a good idea to pass around the length of the array in a separate parameter so you know how big the array is!
Common Pitfalls
- C has no array-bound checks. You won’t even get a warning! If you write past the end of an array, you will simply start overwriting the values of other data in memory.
sizeof(array)will return a different value based on how the variablearraywas declared. Ifarrayis declared asint *array, thenarraywill be considered the size of a pointer. If it was declared asint array[100]then it will be considered the size of 100ints.
Multidimensional Arrays
C lets you declare multidimensional arrays, like int matrix[4][3].
However, it still lays everything out sequentially in memory.
Here’s a visualization of what that matrix looks like conceptually and in memory:

This array occupies (4 * 3 * sizeof(double)) bytes of memory.
Strings
A string is an array of characters (chars), terminated by the null terminator character, '\0'.
In general, the type of a string in C is char*.
String Literals
We have seen string literals so far—a sequence of characters written down in quotation marks, such as "Hello World\n".
The type of a string literal is const char*, so this is valid C:
const char* str = "Hello World\n";
The const shows up here because the characters in a string literal cannot be modified.
Mutable Strings
A mutable string has type char*, without the const.
How can you declare a mutable string with a string literal, if string literals are always const?
Here’s a trick you can use:
remember that, in C, an array is like a pointer to its first element.
So let’s declare the string as an array and give it an initializer:
char str[] = "Hello World\n";
This code behaves exactly as if we wrote:
char str[] = {'H', 'e', 'l', 'l', 'o', ' ', 'W', 'o', 'r', 'l', 'd', '\n', '\0'};
It declares a variable str which is an array of 13 characters (remember that the size of an array may be implicit if we provide an initializer from which the compiler can determine the size), and initializes it by copying the characters of the string "Hello World\n" (including the null terminator) into that array.
String Equality
The expression str1 == str2 doesn’t check whether str1 and str2 are the same string!
Remember, since both of these have a pointer type (char*), C will just compare the pointers.
Instead, if you want to check whether two strings contain equal contents, you will need to use a function like strcmp from the string.h header.
String Copying
Similarly, an assignment like str1 = str2; does not copy strings!
It just just does pointer assignment, so now str1 points to the same region of memory as str2.
Use a function like strcpy if you need to copy characters.
C Macros
Let’s say you have a program that works with arrays of a certain size: say, 100 elements. The number 100 will show up in different parts of the code:
float stuff[100];
// ... elsewhere ...
for (int i = 0; i < 100; ++i) {
do_something(stuff[i]);
}
Repeating the number 100 in multiple locations is not great for multiple reasons:
- It is not maintainable. If you ever need to change the size of the array, you need to carefully look for all the places where you mentioned 100 and change it to something else. If you happen to miss one, subtle bugs will arise.
- It is not readable. Writing code is as much about communicating with other programmers as it is about communicating with the machine! When a human sees the number 100 appear out of nowhere, it can be mysterious and worrisome. For this reason, programmers often call these arbitrary-seeming constants magic numbers (in a derogatory way).
C has a feature called the preprocessor that can cut down on duplication, eliminate magic numbers, and make code more readable. In particular, you can use a macro definition to give your constant a name:
#define NUMBER_OF_THINGS 100
The syntax #define <macro> <expression> defines a new name, the macro, and instructs the preprocessor to replace that name with the given expression.
(Notably, there is no semicolon after preprocessor directives like #define.)
It is a convention to always use SHOUTY_SNAKE_CASE for macro names to help visually distinguish them from ordinary C variable names.
In this example, the C preprocessor will “find and replace” all occurrences of NUMBER_OF_THINGS in our program and replace it with the expression 100.
So it means exactly the same thing to rewrite our program above like this:
#define NUMBER_OF_THINGS 100
float stuff[NUMBER_OF_THINGS];
// ... elsewhere ...
for (int i = 0; i < NUMBER_OF_THINGS; ++i) {
do_something(stuff[i]);
}
The C preprocessor runs before the actual compiler, so you can think of it as doing a textual “find and replace” operation before compiling your code.
Dynamic Memory Allocation
Motivation
Suppose we wanted to write a function that takes an integer, creates an array of the size specified by the integer, initializes each field, and returns the array back to the caller. Given the tools we have thus far, our code might look like this:
// Broken code! Do not do this!
int *initArray(int howLarge) {
int myArray[howLarge];
for (int i = 0; i < howLarge; i++) {
myArray[i] = i;
}
return myArray;
}
The reason this code will not work is that the array is created on the stack. Variables on the stack exist only until the function ends, at which point the stack frame is popped. You can’t use the memory for that stack frame anymore, and it will get reused for some other data.
Dynamic memory allocation lets you obtain memory on the heap instead of the stack. Unlike stack frames, the heap is forever: it remains even when the function returns. Instead, you have to remember to explicitly free the memory when you are done using it.
Both the stack and the heap can grow and shrink over time, as the program creates and destroys stack frames and heap-allocated memory regions. Typically, systems lay out the stack at higher addresses in memory and the heap at lower addresses in memory; as they grow, the stack grows “down” and the heap grows “up.” Here’s a diagram that depicts this growth in the address space:
The diagram also includes static data (globals and constants) and code, which are other memory regions distinct from the heap and stack.
malloc
To use dynamic memory allocation functions, #include <stdlib.h>.
Check out the reference for the stdlib.h header.
To allocate memory on the heap, use the malloc function.
Here’s its declaration:
void* malloc(size_t size);
The return type of malloc is void*, which looks a little weird, but it means “a pointer to some type but I’m not sure which.”
The only argument is a size: the number of bytes you want to allocate.
(size_t is an unsigned integer type.)
How do you know how many bytes you need?
The best way is to use C’s sizeof operator.
Use sizeof(int), for example, to get the number of bytes that an int occupies.
For example, here’s how to allocate space for an int on the heap:
int* intPtr = malloc(sizeof(int));
If you want to get fancy, you can even avoid repeating the int type by using sizeof’s ability to get the type of a variable for you:
int* intPtr = malloc(sizeof(*intPtr));
And here’s how to allocate space for an array of 500 floats:
float* floatArray = malloc(500 * sizeof(*floatArray));
(Please use sizeof instead of guessing the sizes of things, even if you think you know that an int occupies 4 bytes. Because types can be different sizes on different platforms, using sizeof will make your code portable.)
free
Unlike stack variables, you are responsible for freeing memory that you malloc!
You do that with the free function.
free just takes one argument: the pointer to some memory previously allocated with malloc.
Remember this rule: every time you call malloc, remember to put a free somewhere to balance it out.
initArray Revisited
Here’s a fixed version of the code above:
int *initArray(int howLarge) {
int *array = malloc(howLarge * sizeof(*array));
if (array != NULL) {
for (int i = 0; i < howLarge; i++) {
array[i] = i;
}
}
return array;
}
Of course, the caller of initArray will need to call free when it is finished with the memory.
Notice how the above code checks whether malloc returns NULL. It is possible that the heap could run out of space and that there is not enough memory to fulfill the current request. In such cases, malloc will return NULL instead of a valid pointer to a location on the heap. It is a good idea to check the value returned by malloc and make sure that it is not NULL before trying to use the pointer. If the value is NULL, the program should gracefully abort with an error message explaining that a call to malloc failed (or if it can recover from the situation and continue—that is even better).
realloc
The realloc function can reallocate a block of memory at a different size.
In general, realloc might
allocate a new (larger or smaller) block of memory, copy the contents of the original to the new one, and free the old one.
(But it might do something faster if it can avoid it, e.g., if there is room to expand the allocated region “in place.”)
RISC-V Assembly Resources
CS 3410 uses the 64-bit RISC-V (pronounced risk-five) instruction set architecture (ISA). RISC-V is a modern reduced instruction set computer (RISC) architecture. RISC-V is unique because it’s an open instruction set that anyone can implement without any kind of licensing. (That’s in contrast to the two most popular ISAs, Arm and x86, which both require expensive licenses to implement in hardware.)
Here are some references you might find helpful when writing and reading RISC-V assembly code.
Reference Materials
- Use a shorter reference card:
- MIT’s RISC-V reference card is a compact reference for all of the instructions in the 32-bit ISA. But remember that, in 3410, we use the 64-bit version of the ISA, so there are some missing instructions and some subtly differing semantics.
- This exhaustive reference sheet contains instructions for the 32-bit version, 64-bit version, and beyond.
- For the definitive description of what every instruction does and how it’s encoded, see the official ISA manual. It’s long, though, and can get a little bit technical.
Online Tools
- Cornell’s new experimental RISC-V interpreter supports 64-bit RISC-V, and replaces the previous 32-bit interpreter. Note that the old interpreter, which is now deprecated, was designed for the 32-bit ISA, while the new version more closely aligns with the 64-bit ISA taught in class.
- Venus is a powerful interactive RISC-V simulator. It is more complicated to use, but it supports more RISC-V instructions.
Switches and Numbers
Course Overview
CS 3410 is about how computers actually work. That puts it in contrast to other kinds of courses that at other “levels” in the computer science stack:
- Classes like CS 1110, CS 2110, and CS 3110 are all about how to make computers do things. You used programming languages (Python, Java, and OCaml) to write programs without worrying to much about how those languages actually do what they do.
- Classes on application topics like robotics, machine learning, and graphics are all about things computers can do. These are important, of course, because they are the reason we study computing in the first place.
- Outside of CS, and below the 3410 “level,” there are many classes at Cornell on topics like electronics, chemistry, and physics that can tell you physical details of how computers work. That’s not what 3410 is about either: we will build abstractions over those physical phenomena to understand how computers work in the realm of logic.
Switches
The fundamental computational building block in the physical world is a switch. What we mean by a “switch” is: something that controls a physical phenomenon that you can abstractly think of as being in an “on” or “off” state. Some examples of switches include:
- A valve controls hydraulic states, i.e., whether water is flowing or not.
- A vacuum tube controls an electronic signal.
- The game Turing Tumble controls signals in the form of marbles. Yes, you can build real computers out of little plastic levers.

What you think of as a “real” computer controls electronic signals. Aside from vacuum tubes, a particularly easy-to-understand type of electronic switch is a relay. To make a relay, you need:
- An electromagnet (i.e., a magnet controlled by an electronic signal).
- A bendy piece of metal that can be attracted or repelled by that magnet.
- Another piece of metal next to that one. You position it carefully so there’s a tiny gap between the two pieces of metal. When the electromagnet is on, it either closes or opens that gap (depending on whether it attracts or repels the bendy piece of metal).
- Wires hooked up to the two pieces of metal. This way, you can think of the relay as a wire that is either connected or disconnected, depending on whether the electromagnet is charged.
The point is that a relay is a switch that both controls an electronic signal and is controlled by an electronic signal. That’s a really powerful idea, because it means you can wire up a whole bunch of relays to make them control each other! And that is basically what you need to build a computer.
Transistors
Computers today are universally built out of transistors. Transistors work like relays, in the sense that they let one electronic signal control another one. The difference is that they are solid-state devices, relying on the chemistry of the materials inside of them to do the current control instead of a physically moving bendy piece of metal. But abstractly, they do exactly the same thing.
The first transistor was built in Bell Labs in 1947. These days, you can buy them on Amazon for a few pennies apiece. You can build computers “from scratch” by buying a bunch of transistors on Amazon and wiring them up carefully.
Modern computers consist of billions of transistors, manufactured together in an integrated circuit. For example, Apple’s M4 is made up of 28 billion transistors. There is an entire industry of silicon manufacturing that is dedicated to building chunks of silicon and with many, many tiny transistors and wires on them.
Abstractly speaking, however, these integrated circuits are no different from a bunch of transistors you can buy on Amazon, wired up very carefully. Which are in turn (abstractly!) the same as relays, or valves, or Turing Tumble marble levers: they are all just a bunch of switches that control each other in careful ways.
Bits
Because computers are made of switches, data is made of bits. A bit is an abstraction of a physical phenomenon that can either be “on” or “off.” The mapping between the physical phenomenon and the 0 or 1 digit is arbitrary; this is just something that humans have to make up. For example
- In a hydraulic computer, maybe 0 is “no water” and 1 is “water is flowing.”
- In Turing Tumble, perhaps 0 is “marble goes left” and 1 is “marble goes right.”
- In an electronic computer, let’s use 0 to to mean “low voltage” and 1 to mean “high voltage.”
Binary Numbers
Armed with switches and a logical mapping, computers have a way to represent numbers! Just really small numbers: a bit suffices to represent all the integers in interval [0, 1]. It would be nice to be able to represent numbers bigger than 1.
We do that by combining multiple bits together and counting in binary, a.k.a. “base 2.”
In elementary school math class, you probably learned about “place values.” The rightmost digit in a decimal number is for the ones, the next one is for tens, and the next one is for hundreds. In other words, if you want to know what the string of decimal digits “631” means, you can multiply each digit by its place value and add the results together:
63110=1×100+3×101+6×102
We’ll sometimes use subscripts, like nb, to be explicit when we are writing a number in base b.
That’s the decimal, a.k.a. “base 10,” system for numerical notation. Base 2 works the same way, except all the place values are powers of 2 instead of powers of 10. So if you want to know what the string of binary digits “101” represents, we can do the same multiply-and-add dance:
1012=1×20+0×21+1×22
That’s five, so we might write 1012=510.
Some Important Bases
We won’t be dealing with too many different bases in this class. In computer systems, only three bases are really important:
- Binary (base 2).
- Octal (base 8).
- Hexadecimal (base 16), affectionately known as hex for short.
Octal works exactly as you might expect, i.e., we use the digits 0 through 7. For hexadecimal, we run out of normal human digits at 9 and need to invent 6 more digits. The universal convention is to use letters: so A has value 10 (in decimal), B has value 11, and F has value 15.
Converting Between Bases
Here are two strategies for converting numbers between different bases. In both algorithms, it can be helpful to write out the place values for the base you’re converting to. We’ll convert the decimal number 637 to octal as an example. In octal, the first few place values are 1, 8, 64, and 512.
Left to Right
First, compute the first digit (the most significant digit) finding the biggest place value you can that is less than that number. Then, find the largest number you can multiply by that place value. That’s your converted digit. Take that product (the place value times that largest number) and subtract it from your value. Now you have a residual value; start from the beginning of these instructions and repeat to get the rest of the digits.
Let’s try it by converting 637 to octal.
- The biggest place value under 636 is 512. 512×2 doesn’t stay “under the limit,” so we have to settle for 512×1. That means the first digit of the converted number is 1. The residual value is 637−512×1=125.
- The value that “fits under” 125 is 64×1. So the second digit is also 1. The residual value is 125−64×1=61.
- We’re now at the second-to-least-significant digit, with place value 8. The largest multiple that “fits under” 61 is 8×7, so the next digit is 7 and the residual value is 61−8×7=5.
- This is the ones place, so the final digit is 5.
So the converted value is 11758.
Right to Left
First, compute the least significant digit by dividing the number by the base, b. Get both the quotient and remainder. The remainder is the number of ones you have, so that’s your least significant digit. The quotient is the number of bs you have, so that’s the residual value that we will continue with.
Next, repeat with that residual value. Remember, you can think of that as the number of bs that remain. So when we divide by b, the remainder is the number of bs and the quotient is the number of b2s. So the remainder is the second-to-least-significant digit, and we can continue around the loop with the quotient. Stop the loop when the residual value becomes zero.
Let’s try it again with 637.
- 637÷8=79 with remainder 5. So the least significant digit is 5.
- 79÷8=9 with remainder 7. So the next-rightmost digit is 7.
- 9÷8=1 with remainder 1. The next digit is 1.
- 1÷8=0 with remainder 1. So the final, most significant digit is 1.
Fortunately, this method gave the same answer: 11758.
Programming Language Notation
When writing, we often use the notation 11758 to be explicit that we’re writing a number in base 8 (octal). Subscripts are hard to type in programming languages, so they use a different convention.
In many popular programming languages (at least Java, Python, and the language we will use in 3410: C), you can write:
0b10110to use binary notation.0x123abcto use hexadecimal notation.
Octal literals are a little less standardized, but in Python, you can use 0o123 (with a little letter “o”).
Addition
To add binary numbers, you can use the elementary-school algorithm for “long addition,” with carrying the one and all that. Just remember that, in binary, 1+1 = 10 and 1+1+1 (i.e., with a carried one) is 11.
Signed Numbers
This is all well and good for representing nonnegative numbers, but what if you want to represent −10110? Remember, everything must be a bit, so we can’t use the − sign in our digital representation of negative numbers.
There is an “obvious” way that turns out to be problematic, and a less intuitive way that works out better from a mathematical and hardware perspective. The latter is what modern computers actually use.
Sign–Magnitude
The “obvious” way is sign–magnitude notation. The idea is to reserve the leftmost (most significant) bit for the sign: 0 means positive, 1 means negative.
For example, recall that 710=1112.
In a 4-bit sign–magnitude representation, we would represent positive 7 as 0111 and −7 as 1111.
Sign–magnitude was used in some of the earliest electronic computers. However, it has some downsides that mean that it is no longer a common way to represent integers:
- It leads to more complicated circuits to implement fundamental operations like addition and subtraction. (We won’t go into why—you’ll have to trust us on this.)
- Annoyingly, it has two different zeros! There is as “positive zero” (
0000in 4 bits) and a “negative zero” (1000). That just kinda feels bad; there should only be one zero, and it should be neither positive nor negative.
Two’s Complement
The modern way is two’s complement notation.
In two’s complement, there is still a sign bit, and it is still the leftmost (most significant) bit in the representation.
1 in the sign bit still means negative, and 0 means positive or zero.
For the positive numbers, things work like normal.
In a 4-bit representation, 0001 means 1, 0010 means 2, 0011 means 3, and so on up to 0111, which means positive 7.
The key difference is that, in two’s complement, the negative numbers grow “up from the bottom.”
(In the same sense that they grow “down from zero” in sign–magnitude.)
That means that 1000 (and in general, “one followed by all zeroes”) is the most negative number: with 4 bits, that’s −8.
Then count upward from there: so 1001 is −7, 1010 is −6, and so on up to 1111, which is −1.
Here’s another way to think about two’s complement: start with a normal, unsigned representation and negate the place value of the most significant bit. In other words: in an unsigned representation, the MSB has place value 2n−1. In a two’s complement representation, all the other place values remain the same, but the MSB has place value −2n−1 instead.
Here are some cool facts about two’s complement numbers, when using n bits:
- The all-zeroes bit string always represents 0.
- The all-ones bit string always represents −1.
- The biggest positive value, sometimes known as
INT_MAX, is0followed by all ones. Its value is 2n−1−1. - The biggest negative value, sometimes known s
INT_MIN, is1followed by all zeroes. Its value is −2n−1. - Addition works the same as for normal, unsigned binary numbers. You can just ignore the fact that one of the bits is a sign bits, add the two numbers as if they were plain binary values, and you get the right answer in a two’s complement representation!
- To negate a number
i, you can compute~i + 1, where~means “flip all the bits, so every zero becomes one and every one becomes zero.”
Introduction and C
Syllabus and Setup
Please carefully read over the syllabus. Seriously! There is a lot in there that you will want to know.
In case you didn’t already hear it via the rumor mill, CS 3410 is changing. We have updated the curriculum this time around to focus on the essential topics we believe are critical to anyone studying computer science. Among many other changes, this means that there is more focus on programming in C and assembly, we regretfully needed to sacrifice all the digital-design assignments that used the Logisim for visual circuit design, and there is much more of an emphasis on parallelism (because, in the modern era, all computers are parallel).
There are two things you need to do this week:
- An introductory survey on Gradescope. This is due on Friday.
- Set up the RISC-V infrastructure that you will need for all assignments. Please make sure you get this done before your first lab section. If you need help, please post on Ed or find a TA in office hours.
This week’s assignment is the printf assignment.
It serves as an introduction to the C programming language and lets you exercise your skills with numerical representation, binary, and other bases.
As with every assignment in this class, the lab is there to help you get started on the assignment.
The lab instructors will help guide you through “step 0” for the printf assignment; then, the rest is up to you.
Recap: Two’s Complement
Let’s use a six-bit two’s complement representation. What numbers (in standard decimal notation) do these bit patterns represent?
011000111111111011
The answers are:
- 24. For positive numbers (where the sign bit is
0), you don’t have to think much about two’s complement; just read the remaining bits as a normal binary number. - −1. Remember the tip from last time: the all-ones bit pattern is always −1.
- −5. There are many ways to get here. One option is to notice that this number is exactly 1002 less than the all-ones bit pattern, so it’s −1−4.
Hello, C!
Much of the work for CS 3410 will consist of programming in C. If you have mainly programmed in the other Cornell-endorsed languages (Python, Java, and OCaml), the main difference you’ll notice in C is that it operates at a much lower level of abstraction. It gives you a far greater level of control over exactly what the computer does.
While this kind of low-level control is undeniably inconvenient and verbose, it has some extremely important advantages. The most common reasons to use a low-level language like C are:
- Performance. Higher-level languages trade off convenience for speed. Often, programming in a low-level language is the only way to get the kind of efficiency you need.
- Interactions with hardware. When you’re writing an operating system, a device driver, or anything else that interacts with hardware directly, you really need a low-level language.
There are other low-level languages that have the same advantages, such as C++ and Rust. However, C is unique because of its central position in the modern computing landscape. We can confidently say that almost everything you’ve ever done with a computer has eventually relied on software written in C. As just a few examples:
- The Linux kernel is written in C.
- The primary implementation of Python is written in C.
- The C standard library is the de facto standard way that software interacts with operating systems. Even Rust programs rely on C’s standard library for things like printing to the console and opening files.
- In general, whenever two different languages want to talk to each other, they go through C (via a foreign function interface).
Getting Started
Let’s write the smallest possible C program:
int main() {
return 0;
}
Even this minimal program brings up a few basic things about C:
- In basic ways, the syntax looks a little like Java.
There are curly braces and semicolons.
There is even a type called
int. (This is because the designers of Java based its syntax on C.) - Unlike Java, however, there is no class definition here.
You just write a
mainfunction at the top level; it’s not a method on some class. In fact, C doesn’t have classes or objects at all. - C is a statically typed language (like Java but not like Python).
This means that C makes you declare the types of everything you write down.
This example shows one type: the return type of the
mainfunction isint. - That
return 0formaindetermines the exit status for your program.
Let’s run our program.
The commands you see here will assume you have followed our guide to setting up 3410’s RISC-V infrastructure, including setting up the rv alias.
The rv alias works as a prefix that gives you access to the tools you need, so you can type any command you like after it.
For example, you can type:
$ rv ls
and you’ll see similar results to running plain old ls.
Let’s compile the program, like this:
$ rv gcc minimal.c
where minimal.c is the name of the source file.
GCC is the name of the compiler we’ll be using in this course.
That worked, but we actually recommend providing some more command-line options to the compiler whenever you use it.
You can copy and paste our recommended options from the C compilation page.
Then, add -o minimal to tell GCC where to put the output file (if you don’t, GCC picks the name a.out).
So here’s a complete command:
$ rv gcc -Wall -Wextra -Wpedantic -Wshadow -Wformat=2 -std=c17 -o minimal minimal.c
That produces an executable file, minimal.
Now let’s run it:
$ rv qemu minimal
That runs the QEMU emulator to execute the compiled minimal program.
It won’t print anything at all!
Printing
Here’s a slightly more exciting program:
#include <stdio.h>
int main() {
printf("Hello, 3410!\n");
return 0;
}
We’ve added two lines:
- The
#includeis how you import libraries in C. Thestdio.hfile is part of the C standard library, which means it comes with every C compiler. - The
stdio.hfile defines theprintffunction, which is how you print things in C.printfis more powerful than what we’re seeing here; we’ll see more of its power later.
The \n in the string is an escape sequence that means a newline character.
That’s the same as in Java.
Now let’s declare and print a variable:
#include <stdio.h>
int main() {
int n = 3410;
printf("Hello, %d!\n", n);
return 0;
}
We added a variable declaration of n, with type int.
Read more about the basic types in C.
To print out the number, printf exploits format specifiers in the string that you pass to it.
Format specifiers look like %d: they always start with %, followed by a few characters that tell printf how to format stuff.
The d in this one stands for decimal, because that’s the base it uses.
If you have n format specifiers in your printf string, you should pass n extra arguments after the string to printf.
It will print each extra argument using each specified format, in order.
Let’s try some other format specifiers.
%b prints ints in binary, and %x prints them in hex:
#include <stdio.h>
int main() {
int n = 3410;
printf("Decimal: %d\n", n);
printf("Binary: %b\n", n);
printf("Hexadecimal: %x\n", n);
return 0;
}
Read more about format specifiers for printf.
Playing with Numbers
C makes it easy to put our new knowledge about binary numbers and two’s complement into practice.
We’ll use the int8_t type, which is an integer with exactly 8 bits.
(In lots of “normal” code, you can just use int to get a default-sized integer—but for these examples, we really want to use just 8 bits.)
#include <stdio.h>
#include <stdint.h>
int main() {
int8_t n = 7;
printf("n = %hhd\n", n);
return 0;
}
The %hhd format specifier is for printing the int8_t type in decimal.
We also need to #include the stdint.h library to get the int8_t type.
We can also write our 8-bit number in binary notation:
#include <stdio.h>
#include <stdint.h>
int main() {
int8_t n = 0b00000111;
printf("n = %hhd\n", n);
return 0;
}
This should also print 7.
An important thing to reassure yourself is that, in the two programs above, the variable n contains exactly the same value.
There is no difference between the same number specified in decimal notation and binary notation; the choice is just a convenience for the programmer, and the compiler will translate either one into exactly the same value for the computer.
(And that value will be in binary because, of course, everything is bits.)
We can also use the sign bit. What’s this value if we flip the top bit of 7 from 0 to 1?
#include <stdio.h>
#include <stdint.h>
int main() {
int8_t n = 0b10000111;
printf("n = %hhd\n", n);
return 0;
}
That prints -121. Maybe you can convince yourself this is correct by thinking of the largest negative value in 8 bits.
A Little More C
Let’s try the inversion trick from last time:
the identity that, in two’s complement, ~x + 1 is equal to -x.
#include <stdio.h>
#include <stdint.h>
int main() {
int8_t n = 7;
printf("n (binary) = %hhd\n", n);
printf("n (decimal) = %hhb\n", n);
int8_t flipped = ~n + 1;
printf("flipped (binary) = %hhd\n", flipped);
printf("flipped (decimal) = %hhb\n", flipped);
return 0;
}
That worked for 7.
To see a little more of C, let’s try checking that this works for every number we can represent with a char.
#include <stdio.h>
#include <stdint.h>
int8_t flip(int8_t num) {
return ~num + 1;
}
int main() {
for (int8_t i = -128; i < 127; ++i) {
printf("i = %hhd\n", i);
int8_t negated = -i;
int8_t flipped = flip(i);
if (negated != flipped) {
printf("mismatch!\n");
}
}
return 0;
}
This example shows off C’s for loops and if conditions.
If you’re familiar with Java, these should look pretty familiar.
Read more about control flow in C.
It also demonstrates function definitions in C.
If you run this program, there are no mismatches!
So we can be pretty sure this trick works for all the int8_t values, even if you don’t want to try doing the math.
Overflow
Computer representations of integers (usually) have a fixed width, i.e., the number of bits they use:
for example, int8_t always has 8 bits.
This has some fun consequences.
In our last example, we had to think through the minimum and maximum values you can store in an int8_t.
What happens if you exceed this value?
The C language has pretty annoying rules about this.
For signed numbers, it is actually a silent error (a concept known as undefined behavior) to exceed the maximum, e.g., to add 1 to the biggest possible signed number.
But it’s legal to do this for unsigned numbers.
So we’ll try it out with the type uint8_t, which is the unsigned (only-positive) version of our friend int8_t.
Here’s a loop that just adds 1 to an int8_t value many times:
#include <stdio.h>
#include <stdint.h>
int main() {
uint8_t num = 0;
for (int i = 0; i < 500; ++i) {
num += 1;
printf("num = %hhu\n", num);
}
return 0;
}
If you run this program, you’ll see the number counting up from 1. When we reach 255, adding 1 takes us right back down to 0.
It can be helpful to think about the bits.
255 is the all-ones bit pattern: in 8 bits, 1111 1111.
(Sometimes it’s helpful to put spaces in your binary numbers to group together 4 bits, just for legibility.)
Adding one to this will “carry” all the way across, setting every bit to zero.
The last carry bit would go in position 9, but because this is an 8-bit representation, the computer just drops that bit.
And so, the result of the addition 1111 1111 + 0000 0001 is 0000 0000.
This behavior is called integer overflow and it is the source of many fun bugs in all kinds of software.
Memorably, YouTube originally used a signed 32-bit number (i.e., an int) to represent the number of views for a video.
That meant that the largest number of views that any video could have was 232−1−1, or 2,147,483,647 views.
The first video to exceed this number of views was PSY’s “Gangnam Style.”
YouTube made a cute announcement when they had to change that value to a 64-bit integer.
That should be plenty of views for a long time (more than 9 quintillion views).
Prototypes, Headers, Libraries, and Linking
There is a lot more to explore about C programming that you will learn through doing assignments in 3410. But here is one more concept I think will be helpful to see early.
Declarations Must Precede Uses
Here’s a tiny program with one function call:
#include <stdio.h>
void greet(const char* name) {
printf("Hello, %s!\n", name);
}
int main() {
greet("Lefty");
}
(As an aside, void is the “return type” you use for functions that don’t return anything, and const char* is the type of a string literal. We’ll learn more about why the * is in there later in the course.)
A fun quirk about C is that it wants declarations to come before uses.
That means that it won’t work to call greet before we define it, like in this broken program:
#include <stdio.h>
int main() {
greet("Lefty");
}
void greet(const char *name) {
printf("Hello, %s!\n", name);
}
Prototypes, a.k.a. Declarations
As you can imagine, this restriction can get frustrating, and unworkable if you need mutual recursion. The way to fix it is to use a prototype, a.k.a. a declaration. A function declaration looks a lot like a function definition but omits the body. So this program works:
#include <stdio.h>
void greet(const char *name);
int main() {
greet("Lefty");
}
void greet(const char *name) {
printf("Hello, %s!\n", name);
}
We just need to copy and paste the “signature” part of the function definition, put it at the top of the file, and add a semicolon.
That makes it a declaration that means that the call to greet is legal.
Header Files
The need for these declarations is so common that programmers typically put them in a whole separate C source code file, called a header file.
Header files are C files that, by convention, end with a .h instead of a .c and mostly just contain declarations.
So we might put the declaration in greet.h:
void greet(const char *name);
We can use this declaration by #include-ing it:
#include <stdio.h>
#include "greet.h"
int main() {
greet("Lefty");
}
void greet(const char *name) {
printf("Hello, %s!\n", name);
}
Notice the difference between the #include <stdio.h> line and the #include "greet.h" line.
The angle brackets search for built-in library headers;
the quotation marks are for header files you write yourself and tell the compiler to look in the same directory as the source file.
In either case, #include works a lot like just “copying and pasting” the entire text of the file into your source program.
So #include-ing greet.h looks the same to the compiler as a version that just includes the declaration right there.
Separating Source Files
Headers are also part of the mechanism that lets you break up long .c source files.
Let’s say we want to create a separate greet.c library that just contains our greeting function:
#include <stdio.h>
#include "greet.h"
void greet(const char *name) {
printf("Hello, %s!\n", name);
}
Then, our main.c can use the library like this:
#include <stdio.h>
#include "greet.h"
int main() {
greet("Lefty");
}
By “copying and pasting” the contents of greet.h here, the #include sorta works as a way to “import” the greet function so we can use it in main.
Linking Multiple Files
Now, however, we need a way to combine the two .c files into a single executable.
One option is to just give both source files on the command line:
$ rv gcc main.c greet.c -o main
Notice that we don’t list header files when compiling the whole thing: only .c files, not .h files.
Header files are just for #include-ing into other files, so the compiler already sees the contents of those files implicitly.
There’s another way too:
it can be useful to compile the .c files separately and then link them together.
Here’s what that looks like:
$ rv gcc -c main.c -o main.o
$ rv gcc -c greet.c -o greet.o
$ rv gcc main.o greet.o -o main
The first two lines, with -c, compile the source files to object files that end in .o.
Then, the last command links the two object files together into an executable.
Separating it out this way can save you time.
If you only change greet.c, for example, then you only need to re-compile that file and then re-link;
you can skip re-compiling the unchanged main.c.
Floating Point
Like other languages you’ve used before, C has a float type that works for numbers with a decimal point in them:
#include <stdio.h>
int main() {
float n = 8.4f;
printf("%f\n", n * 5.0f);
return 0;
}
But how does float actually work?
How do we represent fractional numbers like this at the level of bits?
The answers have profound implications for the performance and accuracy of any software that does serious numerical computation.
For example, see if you can predict what the last line of this example will print:
#include <stdio.h>
int main() {
float x = 0.00000001f;
float y = 0.00000002f;
printf("x = %e\n", x);
printf("y = %e\n", y);
printf("y - x = %e\n", y - x);
printf("1+x = %e\n", 1.0f + x);
printf("1+y = %e\n", 1.0f + y);
printf("(1+y) - (1+x) = %e\n", (1.0f + y) - (1.0f + x));
return 0;
}
Understanding how float actually works is the key to avoiding surprising pitfalls like this.
Real Numbers in Binary
Before we get to computer representations, let’s think about binary numbers “on paper.” We’ve seen plenty of integers in binary notation; we can extend the same thinking to numbers with fractional parts.
Let’s return to elementary school again and think about how to read the decimal number 19.64. The digits to the right of the decimal point have place values too: those are the “tenths” and “hundredths” places. So here’s the value that decimal notation represents:
19.6410=1×101+9×100+6×10−1+4×10−2
Beyond the decimal point, the place values are negative powers of ten. We can use exactly the same strategy in binary notation, with negative powers of two. For example, let’s read the binary number 10.01:
10.012=1×21+0×20+0×2−1+1×2−2
So that’s 2+14, or 2.25 in decimal.
The moral of this section is: binary numbers can have points too! But I suppose you call it the “binary point,” not the “decimal point.”
Fixed-Point Numbers
Next, computers need a way to encode numbers with binary points in bits. One way, called a fixed-point representation, relies on some sort of bookkeeping on the side to record the position of the binary point. To use fixed-point numbers, you (the programmer) have to decide two things:
- How many bits are we going to use to represent our numbers? Call this bit count n.
- Where will the binary point go? Call this position e for exponent. By convention, e=0 means the binary point goes at the very end (so it’s just a normal integer), e=−1 means there is one bit after the binary point.
The idea is that, if you read your n bits as an integer i, then the number those bits represent is i×2e. (This should look a little like scientific notation, where you might be accustomed to writing numbers like 34.10×10−5. It’s sort of like that, but with a base of 2 instead of 10.)
For example, let’s decide we’re going to use a fixed-point number system with 4 bits and a binary point right in the middle.
In other words, n=4 and e=−2.
In this number system, the bit pattern 1001 represents the value 10.012 or 2.2510.
It’s also possible to have positive exponents.
If we pick a number system with n=4 and e=2,
then the same bit pattern 1001 represents the value 10012×22=1001002, or 3610.
So positive exponents have the effect of tacking e zeroes onto the end of the binary number.
(Sort of like how, in scientific notation, ×10e tacks e zeroes onto the end.)
Let’s stick with 4 bits and try it out.
If e=−3, what is the value represented by 1111?
If e=1, what is the value represented by 0101?
The best and worst thing about fixed-point numbers is that the exponent e is metadata and not part of the actual data that the computer stores. It’s in the eye of the beholder: the same bit pattern can represent many different numbers, depending on the exponent that the programmer has in mind. That means the programmer has to be able to predict the values of e that they will need for any run of the program.
That’s a serious limitation, and it means that this strategy is not what powers the float type.
On the other hand, if programs can afford the complexity to deal with this limitation, fixed-point numbers can be extremely efficient—so they’re popular in resource-constrained application domains like machine learning and digital signal processing.
Most software, however, ends up using a different strategy that makes the exponent part of the data itself.
Floating-Point Numbers
The float type gets its name because, unlike a fixed-point representation, it lets the binary point float around.
It does that by putting the point position right into the value itself.
This way, every float can have a different e value, so different floats can exist on very different scales:
#include <stdio.h>
int main() {
float n = 34.10f;
float big = n * 123456789.0f;
float small = n / 123456789.0f;
printf("big = %e\nsmall = %e\n", big, small);
return 0;
}
The %e format specifier makes printf use scientific notation, so we can see that these values have very different magnitudes.
The key idea is that every float actually consists of three separate unsigned integers, packed together into one bit pattern:
- A sign, s, which is a single bit.
- The exponent, an unsigned integer e.
- The significand (also called the mantissa), another unsigned integer g.
Together, a given s, e, and g represent this number:
(−1)s×1.g×2e−127
…where 1.g is some funky notation we’ll get to in a moment. Let’s break it down into the three terms:
- (−1)s makes s work as a sign bit: 0 for positive, 1 for negative.
(Yes, floating point numbers use a sign–magnitude strategy: this means that +0.0 and -0.0 are distinct
floatvalues!) - 1.g means “take the bits from g and put them all after the binary point, with a 1 in the ones place.” The significand is the “main” part of the number, so (in the normal case) it always represents a number between 1.0 and 2.0.
- 2e−127 is a scaling term, i.e., it determines where the binary point goes. The −127 in there is a bias: this way, the unsigned exponent value e can work to represent a wide range of both positive and negative binary-point position choices.
The float type is actually an international standard, universally implemented across programming languages and hardware platforms.
So it behaves the same way regardless of the language you’re programming in and the CPU or GPU you run your code on.
It works by packing the three essential values into 32 bits.
From left to right:
- 1 sign bit
- 8 exponent bits
- 23 significand bits
To get more of a sense of how float works at the level of bits, now would be a great time to check out the amazing tool at float.exposed.
You can click the bits to flip them and make any value you want.
Conversion Examples
As an exercise, we can try converting decimal numbers to floating-point representations by hand and using float.exposed to check our work.
Let’s try representing the value 8.25 as a float:
- First, let’s convert it to binary: 1000.012
- Next, normalize the number by shifting the binary point and multiplying by 2something: 1.00001×23
- Finally, break down the three components of the float:
- s=0, because it’s a positive number.
- g is the bit pattern starting with
00001and then a bunch of zeroes, i.e., we just read the bits after the “1.” in the binary number. - e=3+127, where the 3 comes from the power of two in our normalized number, and we need to add 127 to account for the bias in the
floatrepresentation.
Try entering these values (0, 00001000…, and 130) into float.exposed to see if it worked.
It’s easiest to enter the exponent in the little text box and the significand by clicking bits in the bit pattern.
Can you convert -5.125 in the same way?
Checking In with C
To prove that float.exposed agrees with C, we can use a little program that reinterprets the bits it produces to a float and prints it out:
#include <stdio.h>
#include <stdint.h>
#include <string.h>
int main() {
uint32_t bits = 0x41020000;
// Copy the to a variable with a different type.
float val;
memcpy(&val, &bits, sizeof(val));
// Print the bits as a floating-point number.
printf("%f\n", val);
return 0;
}
The memcpy function just copies bits from one location to another.
Don’t worry about the details of how to invoke it yet; we’ll cover that later in 3410.
Special Cases
Annoyingly, we haven’t yet seen the full story for floating-point representations.
The above rules apply to most float values, but there are a few special cases:
- To represent +0.0 and -0.0, you have to set both e=0 and g=0. (That is, use all zeroes for all the bits in both of those ranges.) We need this special case to “override” the significand’s implicit 1 that would otherwise make it impossible to represent zero. And requiring that e=0 ensures that there are only two zero values, not many different zeroes with different exponents.
- When e=0 but g≠0, that’s a denormalized number. The rule is that denormalized numbers represent the value (−1)s×0.g×2−126. The important difference is that we now use 0.g instead of 1.g. These values are useful to eke out the last drops of precision for extremely small numbers.
- When e is “all ones” and g=0, that represents infinity. (Yes, we have both +∞ and -∞.)
- When e is “all ones” and g≠0, the value is called “not a number” or NaN for short. NaNs arise to represent erroneous computations
The rules around infinity and NaN can be a little confusing. For example, dividing zero by zero is NaN, but dividing other numbers by zero is infinity:
#include <stdio.h>
int main() {
printf("%f\n", 0.0f / 0.0f); // NaN
printf("%f\n", 5.0f / 0.0f); // infinity
return 0;
}
Other Floating-Point Formats
All of this so far has been about one (very popular) floating-point format:
float, also known as “single precision” or “32-bit float” or just f32.
But there are many other formats that work using the same principles but with different details.
A few to be aware of are:
double, a.k.a. “double precision” or f64, is a 64-bit format. If offers even more accuracy and dynamic range than 32-bit floats, at the cost of taking up twice as much space. There is still only one sign bit, but you get 11 exponent bits and 52 significand bits.- Half-precision floating point goes in the other direction: it’s only 16 bits in total (5 exponent bits, 10 significand bits).
- The bfloat16 or “brain floating point” format is a different 16-bit floating-point format that was invented recently specifically for machine learning. It is just a small twist on “normal” half-precision floats that reallocates a few bits from the significand to the exponent (8 exponent bits, 7 significand bits). It turns out that having extra dynamic range, at the cost of precision, is exactly what lots of deep learning models need. So it has very quickly become implemented in lots of hardware.
Some General Guidelines
Now that you know how floating-point numbers work, we can justify a few common pieces of advice that programmers often get about using them:
- Floating-point numbers are not real numbers. Expect to accumulate some error when you use them.
- Never use floating-point numbers to represent currency. When people say $123.45, they want that exact number of cents, not $123.40000152. Use an integer number of cents: i.e., a fixed-point representation with a fixed decimal point.
- If you ever end up comparing two floating-point numbers for equality, with
f1 == f2, be suspicious. For example, try0.1 + 0.2 == 0.3to be disappointed. Consider using an “error tolerance” in comparisons, likeabs(f1 - f2) < epsilon. - Floating-point arithmetic is slower and costs more energy than integer or fixed-point arithmetic. You get what you pay for: the flexibility of floating-point operations mean that they are fundamentally more complex for the hardware to execute. That’s why many practical machine learning systems convert (quantize) models to a fixed-point representation so they can run efficiently.
For many more details and much more advice, I recommend “What Every Computer Scientist Should Know About Floating-Point Arithmetic” by David Goldberg.
Data Types in C
Type Aliases
Don’t like the names of types in C? You can create type aliases to give them new names:
#include <stdio.h>
typedef int number;
int main() {
number x = 3410;
int y = x / 2;
printf("%d %d\n", x, y);
}
Use typedef <old type> <new type> to declare a new name.
This admittedly isn’t very useful by itself, but it will come in handy as types get more complicated to write.
See the C reference pages on typedef for more.
Structures
In C, you can declare structs to package up multiple values into a single, aggregate value:
#include <stdio.h>
struct point {
int x;
int y;
};
void print_point(struct point p) {
printf("(%d, %d)\n", p.x, p.y);
}
int main() {
struct point location = {4, 10};
location.y = 2;
print_point(location);
}
Structs are a little like objects in other languages (e.g., Java), but they don’t have methods—only fields. You use “dot syntax” to read and write the fields. This example also shows off how to initialize a new struct, with curly brace syntax:
struct point location = {4, 10};
You supply all the fields, in order, in the curly braces of the initializer.
Again, there is a section in the C reference pages for more on struct declarations.
Short Names for Structs
The type of the struct in the previous example is struct point.
It’s common to give structs like these short names, for which typedef can help:
#include <stdio.h>
typedef struct {
int x;
int y;
} point_t;
void print_point(point_t p) {
printf("(%d, %d)\n", p.x, p.y);
}
int main() {
point_t location = {4, 10};
location.y = 2;
print_point(location);
}
This version uses a typedef to give the struct the shorter name point_t instead of struct point.
By convention, C programmers often use <something>_t for custom type names to make them stand out.
Enumerations
There is another kind of “custom” data type in C, called enum.
An enum is for values that can be one of a short list of options.
For example, we can use it for seasons:
#include <stdio.h>
typedef enum {
SPRING,
SUMMER,
AUTUMN,
WINTER,
} season_t;
int main() {
season_t now = SUMMER;
season_t next = AUTUMN;
printf("%d %d\n", now, next);
return 0;
}
We’re using the same typedef trick as above to give this type the short name season_t instead of enum season.
Enums are useful to avoid situations where you would otherwise use a plain integer. They’re more readable and maintainable than trying to keep track of which number means which season in your head.
There is a reference page on enums too.
Bit Packing
Structs work well when you want to combine several types that have “nice” sizes: 1, 4, or 8 bytes, for example.
But they can waste space if you actually only need a few bits for your values.
For example, we learned that the float type is 32 bits: 1 sign bit, 8 exponent bits, and 23 significand bits.
If we wanted to “fake” a floating-point number with a struct, we couldn’t use a 1-bit and 23-bit type.
The best we can do is to use 8 bits, 8 bits, and 32 bits:
#include <stdio.h>
#include <stdint.h>
typedef struct {
uint8_t sign;
uint8_t exponent;
uint32_t significand;
} fake_float_t;
int main() {
printf("size: %lu\n", sizeof(fake_float_t));
}
That struct uses a total of 6 bytes for its fields.
But compilers often need to insert padding to make sure values are aligned for efficient memory access, so the struct can be bigger than that.
Here, we use sizeof to measure the actual total size of the struct, which is 8 bytes—twice as big as a real 4-byte float!
This section will show you how to pack these irregularly-sized values into integers—a trick that you can call bit packing.
The big idea is to treat integer types like uint32_t just as sequences of bits rather than as actual integers, and to use C’s built-in bit-manipulation operations to insert and extract ranges of bits.
The key operations are:
- Masking, with the bitwise “and” operator,
&. - Combining, with the bitwise “or” operator,
|. - Shifting, with the bitwise shift operators
>>and<<.
You may find it helpful to look over the full list of arithmetic and bit manipulation operators in C.
Shifting
In C, i << n shifts the bits in an integer i leftward by n places,
filling in the bottom n bits with zeroes.
Mathematically, this has the effect of multiplying i by 2n:
#include <stdio.h>
#include <stdint.h>
int main() {
uint32_t n = 21;
printf("double n: %u\n", n << 1);
}
Similarly, i >> n shifts the bits rightward by n places, so it multiplies i by 2−n.
These shift operations are useful for moving bit patterns around within the range of bits in the value.
Let’s try moving a value around in a uint32_t and printing out the bits:
#include <stdio.h>
#include <stdint.h>
int main() {
uint32_t n = 21;
printf("%032b\n", n);
printf("%032b\n", n << 8);
printf("%032b\n", n << 16);
printf("%032b\n", n << 24);
}
That %032b specifier tells printf to pad the value out to 32 bits for consistency.
If you run this program, you can see the bit-pattern for the value 21 moving around within the range of 32 bits:
00000000000000000000000000010101
00000000000000000001010100000000
00000000000101010000000000000000
00010101000000000000000000000000
Combining
The bitwise “or” operator, written in C with a single |, is useful for combining different values that have been shifted to different places.
The insight is that x | 0 == x for any bit x, and our shifted values have zeroes wherever they are “inactive.”
Let’s try shifting two different small values to two different positions and then combining them:
#include <stdio.h>
#include <stdint.h>
int main() {
uint32_t x = 21;
uint32_t y = 17;
printf("x: %032b\n", x);
printf("y<<8: %032b\n", y << 8);
printf("x|y<<8: %032b\n", x | (y << 8));
}
If you run this program, you can see the bit patterns for 21 and 17 coexisting happily, side-by-side. Because we know these values fit in 8 bits, we can think of the first value occupying bits 0 through 7 (numbered from the least significant bit) and the next one occupying bits 8 through 15 in the combined value.
Masking
Next, we want a way to extract bits out of one of these combined values.
The idea is to use the bitwise “and” operator, &, together with a mask value that has ones exactly where the bits are that we’re interested in.
We’ll use this property of the & operator:
- Wherever
maskis 1,mask & x == xfor any bitx. - Wherever
maskis 0,mask & x == 0for any bit0.
So a mask value has the effect of preserving values from x where it’s 1 and ignoring them (turning them into to 0) where it’s 0.
Let’s construct a mask to separate the two packed values from last time:
#include <stdio.h>
#include <stdint.h>
int main() {
uint32_t x = 21;
uint32_t y = 17;
uint32_t comb = x | (y << 8);
printf("comb: %032b\n", comb);
uint32_t x_mask = 0b00000000000000000000000011111111;
uint32_t y_mask = 0b00000000000000001111111100000000;
printf("comb&x_mask: %032b\n", comb & x_mask);
printf("comb&y_mask: %032b\n", comb & y_mask);
}
Running this program will show how we’ve “separated” the combined value back into its constituent parts.
When writing masks, it can get really tiresome to write all those ones and zeroes out.
It’s often more practical to write them as hexadecimal literals, remembering that every hex digit corresponds to 4 bits (a nibble):
hex 0 is binary 0000,
and hex F is binary 1111.
So this program is equivalent:
#include <stdio.h>
#include <stdint.h>
int main() {
uint32_t x = 21;
uint32_t y = 17;
uint32_t comb = x | (y << 8);
printf("comb: %032b\n", comb);
uint32_t x_mask = 0x000000FF;
uint32_t y_mask = 0x0000FF00;
printf("comb&x_mask: %032b\n", comb & x_mask);
printf("comb&y_mask: %032b\n", comb & y_mask);
}
Putting it All Together
Now that we’ve separated the two values out by masking the combined value, there is one more step to recover the original values.
We just need to shift them right with >> back to their original positions.
Actually, x is already in its original position, so we don’t have to do anything to it.
But y was shifted left by 8 bits originally, so to get its original value, we’ll shift the masked-out value right again by the same amount.
Here’s a complete program that shows the combination and extraction together:
#include <stdio.h>
#include <stdint.h>
uint32_t pack(uint8_t x, uint8_t y) {
return x | (y << 8);
}
uint8_t get_x(uint32_t comb) {
return comb & 0x000000FF;
}
uint8_t get_y(uint32_t comb) {
return (comb & 0x0000FF00) >> 8;
}
int main() {
uint32_t comb = pack(34, 10);
printf("recovered x: %hhd\n", get_x(comb));
printf("recovered y: %hhd\n", get_y(comb));
}
The pack function combines x and y into a single uint32_t.
Then, the get_x and get_y functions use masking and shifting to undo this combination and extract the original values.
Bit packing is a superpower that you have unlocked by understanding how values are represented at the level of bits.
Use it to save space when ordinary structs won’t cut it!
Arrays & Pointers
Arrays
Like other languages you have used before, C has arrays. Here’s an example:
#include <stdio.h>
int main() {
int courses[7] = {1110, 1111, 2110, 2112, 2800, 3110, 3410};
int course_total = 0;
for (int i = 0; i < 7; ++i) {
course_total += courses[i];
}
printf("the average course is CS %d\n", course_total / 7);
return 0;
}
You declare an array of 7 ints like this:
int courses[7];
And you can also, optionally, provide an initial value for all of the things in the array, as we do in the example above:
int courses[7] = {1110, 1111, 2110, 2112, 2800, 3110, 3410};
You access arrays like courses[i].
This works for both reading and writing.
You can read more about arrays in the C reference pages.
Pointers
Pointers are (according to me) the essential feature of C. They are what make it C. They are simultaneously dead simple and wildly complex. They can also be the hardest aspect of C programming to understand. So forge bravely on, but do not worry if they seem weird at first. Pointers will feel more natural with time, as you gain more experience as a C programmer.
Memory
Pointers are a way for C programs to talk about memory, so we first need to consider what memory is.
It’s helpful to think of a simplified computer architecture diagram, consisting of a processor and a memory. The processor is where your C code runs; it can do any computation you want, but it can’t remember anything. The memory is where all the data is stored; it remembers a bunch of bits, but it doesn’t do any computation at all. They are connected—imagine wires that allow them to send signals (made of bits) back and forth. There are two things the CPU can do with the memory: it can load the value at a given address of its choosing, and it can store a new value at an address.
Abstractly, we can think of memory as a giant array of bytes. Metaphorically speaking (not actually!), it might be helpful to imagine a C declaration like this:
uint8_t mem[SIZE];
where SIZE is the total number of bytes in your machine.
Several billion, surely.
In this metaphor, the processor reads from memory by doing something like mem[123], and it writes by doing mem[123] = 45 in C.
The “address” works like an index into this metaphorical array of bytes.
Maybe the most important thing to take away from this metaphor is that an address is just bits.
Because, after all, everything is just bits.
You can think of those bits as an integer, i.e., the index of the byte you’re interested in within the imaginary mem array.
A Pointer is an Address
In C, a pointer is the kind of value for memory addresses. You can think of a pointer as logically pointing to the value at a given address, hence the name.
But I’ll say it again, because it’s important: pointers are just bits.
Recall that a double variable and a int64_t variable are both 64-bit values—from the perspective of the computer, there is no difference between these kinds of values.
They are both just groups of 64 bits, and only the way the program treats these bits makes them an integer or a floating-point number.
Pointers are the same way:
they are nothing more than 64-bit values, treated by programs in a special way as addresses into memory.
The size of pointers (the number of bits) depends on the machine you’re running on. In this class, all our code is compiled for the RISC-V 64-bit architecture, so pointers are always 64 bits. (If you’ve ever heard a processor called a “32-bit” or “64-bit” architecture, that number probably describes the size of pointers, among other values. Most modern “normal” computers (servers, desktops, laptops, and mobile devices) use 64-bit processors, but 32-bit and narrower architectures are still commonplace in embedded systems.)
Pointer Types and Reference-Of
In C, the type of a pointer to a value of type T is T*.
For example, a pointer to an integer might have type int*,
and pointer to a floating-point value might be a float*,
and a pointer to a pointer to a character could have type char**.
To reiterate, all of these types are nothing more than 64-bit memory addresses.
The only difference is in the way the program treats those addresses:
e.g., the program promises to only store an int in memory at the address contained in an int*.
In C, you can think of all data in the program as “living” in memory.
So every variable and every function argument exists somewhere in the giant metaphorical mem array we imagined above.
That means that every variable has an address: the index in that huge array where it lives.
C has a built-in operator to obtain the address for any variable.
The & operator, called the reference-of operator, takes a variable and gives you a pointer to the variable.
For example, if x is an int variable, then &x is the address where x is stored in memory, with type int*.
Here’s an example where we use & to get the address of a couple of variables:
#include <stdio.h>
int main() {
int x = 34;
int y = 10;
int* ptr_to_x = &x;
int* ptr_to_y = &y;
printf("ints are %lu bytes\n", sizeof(int));
printf("pointers are %lu bytes\n", sizeof(int*));
printf("x is located at %p\n", ptr_to_x);
printf("y is located at %p\n", ptr_to_y);
return 0;
}
We’re also using the %p format specifier for printf, which prints out memory addresses in hexadecimal format.
(By convention, programmers almost always use hex when writing memory addresses.)
Here’s what this program printed once on my machine:
ints are 4 bytes
pointers are 8 bytes
x is located at 0x1555d56bbc
y is located at 0x1555d56bb8
The built-in sizeof operator tells us that pointers are 8 bytes (64 bits) on our RISC-V 64 architecture, which makes sense.
ints are 4 bytes, as they are on many modern platforms.
The system is free to choose different addresses for variables, so don’t worry if the addresses are different when you run this program—that’s perfectly normal.
In this output, however, the system is telling us that it chose very nearby addresses for the x and y variables: the first 60 bits of these addresses are identical.
The address of x ends in the 4 bits corresponding to the hex digit c (12 in decimal), and y lives at an address ending in 8.
That means that x and y are located right next to each other in memory: y occupies the 4 bytes at addresses …6bb8, …6bb9, …6bba, and …6bbb,
and then the 4 bytes for x begin at the very next address, …6bbc.
In C, it doesn’t matter where you put the whitespace in a pointer declaration.
Although I’ll try to write declarations like int* x; consistently in these pages, this means exactly the same thing as int *x;, and you’ll often see the latter in real-world C code.
You can use whichever you prefer.
Everything Has an Address, Including Pointers
Just to emphasize the idea that, in C, all variables live somewhere in memory,
let’s take a moment to appreciate that ptr_to_x and ptr_to_y are themselves variables.
So they also have addresses:
#include <stdio.h>
int main() {
int x = 34;
int y = 10;
int* ptr_to_x = &x;
int* ptr_to_y = &y;
printf("ints are %lu bytes\n", sizeof(int));
printf("pointers are %lu bytes\n", sizeof(int*));
printf("x is located at %p\n", ptr_to_x);
printf("y is located at %p\n", ptr_to_y);
printf("ptr_to_x is located at %p\n", &ptr_to_x);
printf("ptr_to_y is located at %p\n", &ptr_to_y);
return 0;
}
Always remember: pointers are just bits, pointer-typed variables follow the same rules as any other variables.
Pointers as References, and Dereferencing
While pointers are (like everything else) just bits, what makes them useful is that it’s also possible to think of them in a different way: as references to other values. From this perspective, pointers in C resemble references in other languages you have used: it is the power you need to create variables that refer to other values.
The key C feature that makes this view possible is its * operator,
called the dereference operator.
The C expression *p means, roughly, “take the pointer p and follow it to wherever it points in memory, so I can read or write that value (not p itself).”
You can use the * operator both to load from (read) and store to (write) memory.
Imagine a pointer p of type int*.
Here’s how you read from the place where p points:
int value = *p;
And here’s how you write to that location where p points:
*p = 5;
When you’re reading, *p can appear anywhere in a larger expression too, so you can use *p + 5 to load the value p points to and then add 5 to that integer.
All this means that you can use pointers and dereferencing to perform “remote control” accesses to other variables, in the same way that references work in other programming languages. Here’s an example:
#include <stdio.h>
int main() {
int x = 34;
int y = 10;
int* ptr = &x;
printf("initially, x = %d and y = %d and ptr = %p\n", x, y, ptr);
*ptr = 41;
printf("afterward, x = %d and y = %d and ptr = %p\n", x, y, ptr);
return 0;
}
The point of this example is that modifying *ptr changes the value of x.
It does not, however, change the value of ptr itself:
that still points to the same place.
To emphasize that pointer-typed variables behave like any other variable, we can also try assigning to the pointer variable.
It is absolutely critical to recognize the subtle difference between assigning to *ptr and assigning to ptr:
#include <stdio.h>
int main() {
int x = 34;
int y = 10;
int* ptr = &x;
printf("0: x = %d and y = %d and ptr = %p\n", x, y, ptr);
*ptr = 41;
printf("1: x = %d and y = %d and ptr = %p\n", x, y, ptr);
ptr = &y;
printf("2: x = %d and y = %d and ptr = %p\n", x, y, ptr);
*ptr = 20;
printf("3: x = %d and y = %d and ptr = %p\n", x, y, ptr);
return 0;
}
The thing to pay attention to here is that assigning to ptr just changes ptr itself; it does not change x or y.
(That’s the rule for assigning to any variable, not just pointers!)
Then, when we assign to *ptr the second time, it updates y this time, because that’s where it points.
I hope this kind of “variables that reference other variables” thinking is familiar from using other languages, where references are extremely common. The difference in C is that there is no magic: we get reference behavior out of the “raw materials” of bits, by treating some 64-bit values as addresses in memory. Under the hood, this is how references in other languages are implemented too—but in C, we get direct access to the underlying bits.
Arrays are Mostly Just Pointers
Now that we know about pointers, let’s revisit arrays.
In C, an array is a sequence of values all laid out next to each other in memory.
We can use the & reference-of operator to check out the addresses of the elements in an array:
#include <stdio.h>
int main() {
int courses[7] = {1110, 1111, 2110, 2112, 2800, 3110, 3410};
printf("first element is at %p\n", &courses[0]);
printf(" next element is at %p\n", &courses[1]);
printf(" last element is at %p\n", &courses[6]);
return 0;
}
When I ran this program on my machine once, it told me that the first element of the array was located at address 0x1555d56b90, the next element was at 0x1555d56b94, and so on, with each address increasing by 4 with each element.
Remember that ints are 4 bytes on our platform, so these addresses mean that the elements are packed densely, each one next to the other.
You can think of the array having a base address b. Then, the address of an element at index i has this address:
b+s×i
where s is the size of the elements, in bytes.
Treat an Array as a Pointer to the First Element
In fact, C lets you treat an array itself as if it were a pointer to the first element: i.e., the base address b. This works, for example:
#include <stdio.h>
int main() {
int courses[7] = {1110, 1111, 2110, 2112, 2800, 3110, 3410};
printf("first element is at %p\n", &courses[0]);
printf("the array itself is %p\n", courses);
return 0;
}
And C tells us that, if we treat courses as a pointer, it has the same address as its first element.
From that perspective, it is helpful to think of an array variable as storing of the address of the first element of the array.
One important takeaway from this realization is that C does not store the length of your array anywhere—just a pointer to the first element.
It’s up to you to keep track of the length yourself somehow.
This means that, if you want to pass an array to a function, you can use a pointer-typed argument:
#include <stdio.h>
int sum_n(int* vals, int count) {
int total = 0;
for (int i = 0; i < count; ++i) {
total += vals[i];
}
return total;
}
int main() {
int courses[7] = {1110, 1111, 2110, 2112, 2800, 3110, 3410};
int sum = sum_n(courses, 7);
printf("the average course is CS %d\n", sum / 7);
return 0;
}
If you do, it is always a good idea to pass the length of the array in a separate argument.
The subscript syntax, like vals[i], works the same way for pointers as it does for arrays.
C also lets you declare function arguments with actual array types instead of pointer types. This can quickly get confusing, however, and it has very few benefits over just using pointers—so we recommend against it in essentially every case. Just use pointer types whenever you need to pass an array as an argument to a function.
Pointer Arithmetic
Since we’ve seen that the elements of an array exist right next to each other in memory, can we access them by computing their addresses ourselves?
Absolutely! C supports arithmetic operators like + and - on pointers, but they follow a special rule you will need to remember.
Here’s an example:
#include <stdio.h>
void experiment(int* courses) {
printf("courses = %p\n", courses);
printf("courses + 1 = %p\n", courses + 1);
}
int main() {
int courses[7] = {1110, 1111, 2110, 2112, 2800, 3110, 3410};
experiment(courses);
return 0;
}
The important thing to notice here is that adding 1 to courses increased its value by 4, not by 1.
That’s because the rule in C is that pointer arithmetic “moves” pointers by element-sized chunks.
So because courses has type int*, its element size is 4 bytes.
The rule says that, if you write the expression courses + n, that
will actually add n×4 bytes to the address value of courses.
This may seem odd, but it’s extremely useful:
it means that pointer arithmetic stays pointing to the first byte of an element.
If you think of courses itself as a pointer to the first int in the array, then courses + 1 points to the (first byte of) the second int in the array.
It would be inconvenient and annoying if doing +1 just took us to the second byte in the first element; nobody wants that.
A consequence is that we can use pointer arithmetic directly, along with the dereferencing operator *, to access the elements of an array:
#include <stdio.h>
void experiment(int* courses) {
printf("courses[0] = %d\n", *(courses + 0));
printf("courses[5] = %d\n", *(courses + 5));
}
int main() {
int courses[7] = {1110, 1111, 2110, 2112, 2800, 3110, 3410};
experiment(courses);
return 0;
}
Now that you know how arrays and pointer arithmetic work, you don’t actually need the subscripting operator!
Instead of writing arr[idx], you can always just use *(arr + idx).
It means the same thing.
Here’s a fun but mostly useless fact about C programming.
Since arr[idx] means exactly the same thing as *(arr + idx), and because + is commutative, this also means the same thing as *(idx + arr), which can—by the same rules—also be written as idx[arr].
So if you really want to confuse the people reading your code, you can always write your array indexing expressions backward:
#include <stdio.h>
void experiment(int* courses) {
printf("courses[0] = %d\n", 0[courses]);
printf("courses[5] = %d\n", 5[courses]);
}
int main() {
int courses[7] = {1110, 1111, 2110, 2112, 2800, 3110, 3410};
experiment(courses);
return 0;
}
But this is, uh, not a great idea in the real world, where your code will actually be read by humans with thoughts and feelings.
Strings are Null-Terminated Character Arrays
Our new knowledge about pointers and arrays now lets us revisit another concept we’ve already been using in C:
strings.
You may recall that we previously told you not to worry about why strings in C have the type char*.
Now we can demystify this fact:
strings in C are arrays of char values, each of which is a single character.
On most modern systems (including our RISC-V target), char is a 1-byte (8-bit) type.
So each char in a string is a number between 0 and 28−1, i.e., 255.
Programs use a text encoding to decide which number represents which textual character.
An extremely popular encoding that includes the basic English alphabet is ASCII.
But C saves you the trouble of looking up characters in the ASCII table; you can use a literal 'q' (note the single quotes!) to get a char with the numeric value corresponding to a lower-case q character.
As with any other array in C, a string just consists of a pointer to the first element (the first character in this case).
So when you see char* str, you can think either “str is a string” or “str is the address of the first element of a string.”
Also as with any other array, we need a way to know how many elements there are in the array.
Instead of keeping track of the length as an integer, as we have so far, C strings use a different convention:
they use a null character, with value 0, to indicate the end of a string.
You can write this special character as '\0'.
This means that various functions that process strings work by iterating through all the characters and then stopping when the character is '\0'.
All this means that you can use everything you know about C arrays and apply them to strings. For example:
#include <stdio.h>
void print_line(char* s) {
for (int i = 0; s[i] != '\0'; ++i) {
fputc(s[i], stdout);
}
fputc('\n', stdout);
}
int main() {
char message[7] = {'H', 'e', 'l', 'l', 'o', '!', '\0'};
print_line(message);
return 0;
}
This shows several C array features that are equally useful for strings (character arrays) as they are for any other array:
- Array initialization, with curly braces.
- Treating arrays as pointers to their first element, so we can pass our
chararray to a function expecting achar*. - Using array subscript notation, like
s[i], on the pointer to access the array’s elements.
One important thing to realize here is that, when we initialize this array “manually” using the array initialization syntax, we have to remember to include the null terminator '\0' ourselves.
Ordinary string literals, like "Hello!", include a null terminator automatically.
So these lines are roughly equivalent:
char message[7] = {'H', 'e', 'l', 'l', 'o', '!', '\0'};
char* message = "Hello!";
If you go the manual route and forget the null terminator, bad things will happen.
Try to imagine what might go wrong in this program if we left off the '\0', for example.
There are many possibilities, and none of them are good.
(This is an example of undefined behavior in C, so there is no single answer.)
Fun Pointer Tricks
Here are some useful things you can do with pointers.
Pass by Reference
Pointers are useful for passing parameters by reference. C doesn’t actually have a way to “native” pass-by-reference; everything is passed as a value. But you can pass pointers as values and use those to refer to other values.
For example, this swap function doesn’t work because a and b are passed by value:
#include <stdio.h>
void swap(int x, int y) {
int tmp = x;
x = y;
y = tmp;
}
int main() {
int a = 34;
int b = 10;
printf("%d %d\n", a, b);
swap(a, b);
printf("%d %d\n", a, b);
}
But if we pass pointers instead, we can dereference those pointers so we modify the original variables in place. So this version works:
#include <stdio.h>
void swap(int* x, int* y) {
int tmp = *x;
*x = *y;
*y = tmp;
}
int main() {
int a = 34;
int b = 10;
printf("%d %d\n", a, b);
swap(&a, &b);
printf("%d %d\n", a, b);
}
Null Pointers
Because pointers are just integers, you can set the to zero. Zero isn’t actually a valid memory address. That makes the zero value useful for signaling the absence of data. It’s particularly useful for writing functions with optional parameters.
In C, you can use NULL to get a pointer with value zero.
Here’s an example that extends our swap function to optionally also produce the sum of the values:
#include <stdio.h>
void swap_and_sum(int* x, int* y, int* sum) {
int tmp = *x;
*x = *y;
*y = tmp;
if (sum != NULL) {
*sum = *x + *y;
}
}
int main() {
int a = 34;
int b = 10;
printf("%d %d\n", a, b);
int sum;
swap_and_sum(&a, &b, &sum);
swap_and_sum(&a, &b, NULL);
printf("%d %d\n", a, b);
printf("sum = %d\n", sum);
}
When a pointer might be null, always remember to include a != NULL check before using it.
The possibility of accidentally dereferencing a null pointer is Sir Tony Hoare’s “billion-dollar mistake.”
Pointers to Pointers
The type of a pointer to a value of type T is T*.
That includes when T itself is a pointer type!
So you can create pointers to pointers, and so on.
For example, int** is a pointer to a pointer to an int.
(It’s not common to go any deeper than two levels, but nothing stops you…)
It’s a silly example, but we can make our swap function swap int*s instead of actual ints:
#include <stdio.h>
void swap(int** x, int** y) {
int* tmp = *x;
*x = *y;
*y = tmp;
}
int main() {
int a = 34;
int b = 10;
int* a_ptr = &a;
int* b_ptr = &b;
printf("%d %d\n", a, b);
swap(&a_ptr, &b_ptr);
printf("%d %d\n", a, b);
}
Pointers to Functions
Maybe you have taken CS 3110, so you know it’s cool to pass functions into other functions. C can do that too, kind of! By creating pointers to functions.
The syntax admittedly looks really weird.
You write T1 (*name)(T2, T3) for a pointer to a function that takes argument types T2 and T3 and returns a type T1.
Here’s an example in action:
#include <stdio.h>
int incr(int x) {
return x + 1;
}
int decr(int x) {
return x - 1;
}
int apply_n_times(int x, int n, int (*func)(int)) {
for (int i = 0; i < n; ++i) {
x = func(x);
}
return x;
}
int main() {
int n = 20;
n = apply_n_times(n, 5, &incr);
n = apply_n_times(n, 2, &decr);
printf("n = %d\n", n);
}
Pointers to Anything
Remember that pointers are bits, and all pointers look the same:
they are just memory addresses.
So, if you just look at the bits, there is no difference between an int* and a float* and a char*.
They are all just addresses.
For this reason, C has a special type that means “a pointer to something, but I don’t know what.”
The type is spelled void*.
It is useful in situations where you don’t care what’s being pointed to.
Here’s a simple program that uses a void* to wrap up a call to printf for showing addresses:
#include <stdio.h>
void print_ptr(void* p) {
printf("%p\n", p);
}
int main() {
int x = 34;
float y = 10.0f;
print_ptr(&x);
print_ptr(&y);
}
The Stack, The Heap, the Dynamic Memory Allocation
The Stack
So far, all the data we’ve used in our C programs has been stored in local variables. These variables exist for the duration of the function call—and as soon as the function returns, the variables disappear. All this per-call local-variable storage is part of the function call stack, also known as just the stack.
Don’t confuse the stack with the abstract data type (ADT) that is also called a stack. The stack works like a stack, in the sense that you push and pop elements on one end of the stack. But it’s not just any stack; it’s a special one that the compiler manages for you.
You may have visualized the function call stack when you learned other programming languages. You can draw it with a box for every function call, which gets created (pushed) when you call the function and destroyed (popped) when the function returns. These boxes are called stack frames, or just frames for short (or sometimes, an activation record). For reasons that will become clear soon, when thinking about C programs, it’s important that we draw the stack growing “downward,” so the first call’s frame is at the top of the page.
Here is a mildly interesting C program that uses the stack:
#include <stdio.h>
const float EULER = 2.71828f;
const int COUNT = 10;
// Fill an array, `dest`, with `COUNT` values from an exponential series.
void fill_exp(float* dest) {
dest[0] = 1.0f;
for (int i = 1; i < COUNT; ++i) {
dest[i] = dest[i - 1] * EULER;
}
}
// Print the first `n` values in a float array.
void print_floats(float* vals, int n) {
for (int i = 0; i < n; ++i) {
printf("%f\n", vals[i]);
}
}
int main() {
float values[100];
fill_exp(values);
print_floats(values, 10);
return 0;
}
The values array is part of main’s stack frame.
The calls to fill_exp and print_floats have pointer variables in their stack frames that point to the first element of this array.
Limitations of the Stack
The key limitation of putting your data on the stack comes from this observation: variables only live as long as the function call. So if you want data to remain after a function call returns, local variables (data in stack frames) won’t suffice.
The consequence of this observation is the following rule: never return a pointer to a local variable. When you do, you’re returning a pointer to data that is about to be destroyed. So it will be a mistake (undefined behavior in C) to use that pointer.
On the other hand, both of these things are perfectly safe:
- Passing a pointer to a local variable as an argument to a function. Our example above does this. This is fine because the data exists in the caller’s stack frame, which still exists as long as the callee is running (and longer).
- Returning a non-pointer value stored in a local variable. The compiler takes care of copying return values into the caller’s stack frame if necessary.
To get a sense for why this is limiting, consider our example above.
It’s kinda weird that we have to write a fill_exp function that fills in an exponential series into an array that already exists.
It seems like it would be a little more natural to have a create_exp function that returns an array.
Something like this:
#include <stdio.h>
const float EULER = 2.71828f;
const int COUNT = 10;
// This function has a bug! Do not return pointers to local variables!
float* create_exp() {
float dest[COUNT];
dest[0] = 1.0f;
for (int i = 1; i < COUNT; ++i) {
dest[i] = dest[i - 1] * EULER;
}
return dest;
}
// Print the first `count` values in a float array.
void print_floats(float* vals, int count) {
for (int i = 0; i < count; ++i) {
printf("%f\n", vals[i]);
}
}
int main() {
float* values = create_exp();
print_floats(values, 10);
return 0;
}
That API looks nicer; we can rely on the create_exp function to both create the array and to fill it up with the values we want.
But this program has a serious bug—in C, it has undefined behavior.
When I ran it on my machine, it just hung indefinitely; of course, subtler and worse consequences are also possible.
To see what’s wrong, let’s think about what might happen with the stack in memory.
All the stack frames, and all the local variables, exist at addresses in memory.
When the call create_exp returns, its memory doesn’t literally get destroyed; the memory, literally speaking, still exists in my computer.
But when we do the next call to print_floats, its stack frame takes the space previously occupied by the create_exp frame.
So its local variables, vals and count take up the same space that was previously occupied by the dest array.
The Heap
This create_exp example is not en edge case;
in practice, real programs often need to store data that “outlives” a single function call.
C has a separate region of memory just for this purpose.
This region is called the heap.
As above, don’t confuse the heap with the data structure called a heap, which is useful for implementing priority queues. The heap is not a heap at all. It is just a region of memory.
The key distinction between the heap and the stack is that you, the programmer, have to manage data on the heap manually. The compiler takes care of managing data on the stack: it allocates space in stack frames for all your local variables automatically. Your code needs to explicitly allocate and deallocate regions of memory on the heap whenever it needs to store data that lasts beyond the end of a function call.
C comes with a library of functions for managing memory on the heap,
which live in a header called stdlib.h.
The two most important functions are:
malloc, for memory allocate: Allocate a new region of memory on the heap, consisting of a number of bytes that you choose. Return a pointer to the first byte in the newly allocated region.free: Take a pointer to some memory previously allocated withmallocand deallocate it, freeing up the memory for use by some future allocation.
Here’s a version of our create_exp program that (correctly) uses the heap:
#include <stdio.h>
#include <stdlib.h>
const float EULER = 2.71828f;
const int COUNT = 10;
// Allocate a new array containing `COUNT` values from an exponential series.
float* create_exp() {
float* dest = malloc(COUNT * sizeof(float)); // New!
dest[0] = 1.0f;
for (int i = 1; i < COUNT; ++i) {
dest[i] = dest[i - 1] * EULER;
}
return dest;
}
// Print the first `count` values in a float array.
void print_floats(float* vals, int count) {
for (int i = 0; i < count; ++i) {
printf("%f\n", vals[i]);
}
}
int main() {
float* values = create_exp();
print_floats(values, 10);
free(values); // Also new!
return 0;
}
Let’s look at the new lines in more detail. First, the allocation:
float* dest = malloc(COUNT * sizeof(float));
The malloc function takes one argument: the number of bytes of memory you want.
We want COUNT floating-point values, so we can compute that size in bytes by multiplying that array length by sizeof(float) (which gives us the number of bytes occupied by a single float).
You almost always want to use sizeof in the argument of your malloc calls; this is clearer and more portable than trying to remember the size of a given type yourself.
Next, the deallocation:
free(values);
The free function also takes one argument:
a pointer to memory that you previously allocated with malloc.
This illustrates the cost of manual memory management:
whenever you allocate memory, you take responsibility for deallocating it yourself.
That’s unlike the stack, where the compiler takes care of managing the lifecycle of the memory for you.
(You should never call free on a pointer to the stack.)
The Heap Commandments
Because you manually manage the memory on the heap, it’s possible to make mistakes. There are four big things you must avoid:
- Use after free.
After you
freememory, you are no longer allowed to use it. Your program may not load or store through any pointers into the freed memory. - Double free.
You may only
freememory once. Do not callfreeon already-freed memory. - Memory leak.
You must pair every call to
mallocwith a corresponding call tofree. Otherwise, your program will never “recycle” its memory, so the data will grow until you run out of memory. - Out-of-bounds access.
You must only use the pointer returned from
mallocto access data inside the allocated range of bytes. You can use pointer arithmetic (or array subscripting) to read and write bytes in the range, but nothing before the beginning or after the end of the range.
Even if they seem simple,
C programmers find in practice that these rules are extremely hard to follow consistently.
As software gets more complex, it can be hard to keep track of when memory has been freed, when it still needs to be freed, and what to check to ensure that accesses are within bounds.
Personally, I think following these rules is the hardest part of programming in C (and C++).
And these problems, because they trigger undefined behavior in C, can have extremely serious consequences—not just crashes and misbehavior, but security vulnerabilities.
As an example to illustrate the severity of the problem, a 2019 study by Microsoft found that 70% of all the security vulnerabilities they tracked in their software stemmed from these kinds of memory bugs.
Please reflect on the fact that these problems are really only possible in languages like C and C++, where you are responsible for managing the heap yourself. In contrast, Python, Java, OCaml, Rust, and Swift are all memory safe languages, meaning that they manage the heap automatically for you. This is not just a convenience; these languages can rule out out these extremely dangerous memory bugs altogether. While they give up some performance or control to do so, programmers in these languages find these downside to be an acceptable trade-off to avoid the extreme challenge posed by memory bugs.
Catching Memory Bugs
Let’s try writing a program that intentionally violates the commandments.
Specifically, let’s try adding out-of-bounds reads to our create_exp program:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
const float EULER = 2.71828f;
const int COUNT = 10;
// Allocate a new array containing `COUNT` values from an exponential series.
float* create_exp() {
float* dest = malloc(COUNT * sizeof(float)); // New!
dest[0] = 1.0f;
for (int i = 1; i < COUNT; ++i) {
dest[i] = dest[i - 1] * EULER;
}
return dest;
}
// Print the first `count` values in a float array.
void print_floats(float* vals, int count) {
for (int i = 0; i < count; ++i) {
printf("%f\n", vals[i]);
}
// Let's see what's nearby...
char* ptr = (char*)vals;
for (int j = 0; j < 100; ++j) {
char* byte = ptr - j;
printf("%p: %d %c\n", byte, *byte, *byte);
}
}
// Generate a secret.
char* gen_secret() {
char* secret = malloc(16);
strcpy(secret, "seekrit!");
return secret;
}
int main() {
char* password = gen_secret();
float* values = create_exp();
print_floats(values, 10);
free(values);
free(password);
return 0;
}
This program takes a pointer to our values array, and it first safely walks forward from there to print out the floats it contains.
Then, it does something sneaky: it starts walking backward from the beginning of the array, immediately leaving the range of legal bytes it’s allowed to read.
Because this program violates the commandments, it might do anything:
it might crash, corrupt memory, or just give nonsense results.
But when I ran this on my machine once, it walked all the way into the memory pointed to by password and printed out its contents.
Spooky!
This kind of out-of-bounds read is the basis for many real-world security vulnerabilities.
Since I’m telling you that these bugs are extremely easy to create, is there any way of catching them?
Fortunately, GCC has a built-in mechanism for catching some memory bugs, called sanitizers.
To use them, compile your program with the flags -g -fsanitize=address -fsanitize=undefined:
$ gcc -Wall -Wextra -Wpedantic -Wshadow -Wformat=2 -std=c17 -g -fsanitize=address -fsanitize=undefined heap_bug.c -o heap_bug
Sanitizers check your code dynamically, so this won’t print an error at compile time. Try running the resulting code:
$ qemu heap_bug
If everything works, the sanitizer will print out a long, helpful message telling you exactly what the program tried to do.
Crashing with a useful error is a much more helpful thing to do than behave unpredictably. So whenever you suspect your program might have a memory bug, try enabling the sanitizers to check.
Memory Layout
The stack and the heap are both regions in the giant metaphorical array that is memory.
Both of them need to grow and shrink dynamically:
the program can always malloc more memory on the heap, or it can call another function to push a new frame onto the stack.
Computers therefore need to choose carefully where to put these memory segments so they have plenty of room to grow as the program executes.
In general:
- The heap starts at a low memory address and grows upward as the program allocates more memory.
- The stack starts at a high memory address and grows downward as the program calls more functions.
By starting these two segments at opposite “ends” of the address space, this strategy maximizes the amount of room each one has to grow.
There are also other common memory segments. These ones typically have a fixed size, so “room to grow” is not an issue:
- The data segment holds global variables and constants, which exist for the entire duration of the program. Aside from the global variables you declare yourself, string literals from your program go here.
- The text segment contains the program, as machine code instructions. Much more discussion of these instructions is coming in a couple of weeks.
Gates & Logic
Our goal over the next couple of lectures is to build a computer.
Let’s take it back to the beginning: computers are made out of logical switches. In the modern era, these switches are implemented using transistors. But let’s start with relays instead, because they’re easier to think about.
We won’t build a computer in one step. We’re going to use relays to build bigger components, and then think abstractly about what those components do. Then we can forget about the internals, i.e., how we built the thing, and we can build something even bigger out of that. Step by step, we will climb up the latter of abstraction and build a computer.
Truth Tables
To climb the abstraction latter, we need an abstract way to write down the behavior of a circuit element. Our tool for this is a truth table, which exhaustively describes how the circuit’s input and output signals behave in terms of bits.
Relays have three “ports”: two input ports, which we’ll call c for “control,” in, and out. The c and in ports are both inputs, and the out port is the only output.
Recall how relays have a “default on” and a “default off” variant. (The electromagnet repulses or attracts the bendy piece of metal, respectively.) Truth tables are a good way to write down the difference between the variants.
Here is the truth table for a “default off” relay:
| c | in | out |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Truth tables have one column per port, and they have one row for every combination of input-port values.
Here’s the truth table for the “default on” kind of relay:
| c | in | out |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Building Nand
Let’s build a different circuit using relays as the “raw materials.” We will build a nand (“not and”) function.
It’s important to write down the specification for the function we want. Our specifications will be truth tables. Here’s the truth table for nand:
| a | b | out |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
There are two inputs, a and b, and one output, out.
How can you write up relays to make a circuit with this truth table? Hint: You can do it two relays, one of each kind.
Level Up: Building Not
Here’s the philosophy of this kind of work: now that we’ve built a nand circuit, we earn the right to use it in larger, more interesting circuits. We have leveled up, and we can build something else using nands—and we can forget how nand works internally.
Let’s build a not function next. Here’s the truth table:
| in | out |
|---|---|
| 0 | 1 |
| 1 | 0 |
This circuit is also called an inverter.
Can you use nands to make not?
Keep Leveling Up
We’re going to keep building larger and more interesting circuits out of smaller ones. This “leveling up” sort of feels like a video game. In fact, people have made video games out of this process! A cool one is Nandgame.
Try using Nandgame to build the circuits we already made. Then, try going farther and making and and or circuits.
Logic Notation
It’s going to be helpful to have a notation to write down these logic circuits as we make them more complicated. Here is some common mathy notation that people use to write these operators.
| name | C bitwise op | mathy |
|---|---|---|
| not | ~a | ¯a or ¬a or a′ |
| and | a & b | a∧b or a⋅b or just ab |
| or | a | b | a∨b or a+b |
| xor | a ^ b | a⊕b |
Each of these operators has a visual representation for wiring schematics, but they are too hard to include here. You can see them all on the Wikipedia page for logic gate.
Universal Gates, and a Recipe for Building Anything
Nandgame encourages you to be creative: to think carefully about how to use your “inventory” efficiently to build a new circuit. But there is an easier, more mechanical way that works to build anything: that is, given an arbitrary truth table, this method can give you a circuit.
Here are the steps:
- Start with a truth table.
- For every row where the output is 1, write out the minterms. The minterm is the logical expression that is an “and” of all the input variables, either with or without negation, according to the truth value of the given input. For example, if the row in the truth table has a=1 and b=0, then the minterm is a¯b. The idea is that the minterm completely describes the input condition where that row is active.
- Join all the minterms for those output-1 rows with “ors.” This is the sum-of-products expression.
That gives you a logical expression consisting only of not, and, and or that is 1 when the output in the truth table is 1 and 0 otherwise. You can construct a circuit out of these three gates to match the expression.
Because this sum-of-products process works for any truth table, and it only uses those three gates, you can conclude that the combination of and, not and or is all you really need: if you just have those three functions, you can build any other function.
It gets better: you can each all of and, or, and not through a clever combination of only nand gates. You can also build any of them out of just nor gates. (Try it in Nandgame if you want!) That means that, transitively, you can build any circuit out of just nand or just nor. People call these gates universal for that reason.
Practicing Sum-of-Products Constructions
Here are two functions you can build to try out your newfound skills in building arbitrary circuits out of and, or, and not:
- Try building xnor, i.e., “not xor,” using this technique.
- A multiplexer (aka a mux or a selector) has three inputs: s for “select,” in₀, and in₁. It has one output, out. When s is 0, out is equal to in₀. When s is 1, out is equal to in₁.
Because the multiplexer has 3 inputs, you will want to use 3-input and and or gates. You can, of course, implement these with a cascade of 2-input gates.
Arithmetic
If this technique really works to build “everything,” let’s try using it build math. Starting with addition.
Half Adder
To keep the circuit small, let’s add two 1-bit numbers.
Let’s start by writing out all the possible combinations, and the sum as a binary value. This is not quite a truth table, because the output is a 2-bit number and not a truth value, but it’s close:
| a | b | a+b |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 10 |
To make this into a truth table, let’s separate the two bits of the output sum—and fill in the implicit 0 in the most significant bit. The normal way to do this is to label the two bits c, for the carry bit, and s, for the sum. The truth table looks like this:
| a | b | c | s |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Remember that a and b are the input columns, and c and s are the output columns.
This truth table is a little different from the other ones on this page because it has two outputs. But we can still use the same approach, just one output at a time. That is, we can write the logical formulas for the two outputs separately c=ab and s=¯ab∨a¯b.
It is “fun” to notice that there is another truth table that already matches the behavior of the sum value: namely, s=a⊕b. So we can use two of the gates we built above to make this one-bit adder: an and gate for c and an xor gate for s.
This circuit is usually called a half adder. Why “half”? It’s missing an important feature that we’ll add next.
Full Adder
Adding one-bit numbers is nice, but we would like to add bigger numbers. The insight that will get us there is that, when we do “long addition” of binary numbers, we add up one bit at a time—and possibly “carry the one” to the next column. At each step in this process, we actually need to add three one-bit numbers together: each of the two input bits and—for every bit except the first—the carried bit from the previous column (which may be zero).
So the key to implementing a circuit that does “long addition” is to extend our one-bit adder above to take three inputs instead of two. This thing will be called a full adder. It has three one-bit inputs: a, b, and cin for the carry-in bit. Just like the half adder, it has two one-bit outputs: the sum s and the carry-out bit cout.
Try writing out a truth table for this circuit. One useful thing to remember is that, despite cin having a different-looking name, the three inputs are really indistinguishable: we’re just adding up 3 one-bit numbers here.
We could absolutely use the sum-of-products approach to build the circuit for the full adder. But it turns out that there is a much simpler way to do it by using two half adders and some other logic. Can you build this circuit? You can try skipping to the “full adder” level in Nandgame to try it out.
n-Bit Adder
The full adder is the building block we need to construct an n-bit adder, for any n: a circuit that takes two n-bit numbers and adds them together, producing an (n+1)-bit result. You can make this circuit by chaining together a series of n full adders, hooking the cout of one to the cin of the next.
By climbing the abstraction ladder, we have gradually gotten from relays, something we can physically understand, all the way to a binary calculator. We don’t have a computer yet, exactly, but we do have something pretty cool.
Stateful Logic
The Need for State
So far, we have climbed up the abstraction ladder to build circuits that can do lots of interesting computations on bits. We have an n-bit adder, for example, so maybe you can believe that—using the same principles—we can build more complicated operations: multiplication and even divisor, for example. But I contend that the principles we’ve been using have a fundamental limitation: they are stateless. To build a real computer, we will need a way to store and retrieve information.
To see what I mean by stateless, try inputting a bunch of numbers into an adder (or whatever) in Nandgame. Then, reset all the inputs back to zero. The circuit’s outputs also back down to zero, because they are a function of the current values of the inputs. The circuit has no memory of what happened in the past.
The reason this is a problem is that computers work by iteratively updating stored values, one step at a time. Extending our simplified view of computer architecture, let’s imagine a computer made of three parts:
- The processor logic, with circuits for addition and such.
- The data memory: a mapping from memory addresses to values.
- An instruction: a string of bits that encode some operation for the processor to take, such as “read the values from the data memory at addresses
0xafand0x1cand put the result at address0xe9.”
If the bits of the instruction were exposed via buttons on your machine, you could do computations by sequentially keying in different instructions. The data memory itself clearly needs to be stateful, i.e., to do a thing that our circuits are incapable of so far to keep data around. But let’s pretend that’s someone else’s problem and focus just on the processor for now. Even so, this setup leaves something to be desired: a human would have to manually key in each instruction in sequence. That’s of course not how programs work in real computers; somehow, there’s a way to write a program down up front and then let the computer run through instructions of its own accord.
Let’s extend our architecture diagram with another memory: the instruction memory. This will contain a bunch of bit-strings like our example above, laid out in order. Again, I know this memory itself needs state, but let’s ignore that for now. To make the whole machine work, we will also need a way to keep track of the current instruction we are executing. In real machines, this thing is called the program counter (PC): a stateful element that holds the address in the instruction memory of the currently-executing instruction. This might start out at zero, so we read out the value of the 0th instruction; then, when that instruction is done doing all of its work, we need to increment it to 1 to run the next instruction, and so on.
This program counter needs to be stateful. It needs to keep track of the current value and hold it over time until we decide to change it. Today, we will build circuits that can work like this.
The Clock
Stateful circuits are all about doing things over time: i.e., taking different actions at one point in time vs. another. But how do we define “time”? Stateful circuits usually use a special signal, called a clock to keep track of “logical time.” By “logical time,” we mean time measured in an integer number of clock cycles, as opposed to the continuous world of real time measured in seconds and minutes.
A clock is an input signal to our circuits that oscillates between 0 and 1 in a regular pattern. You can imagine a person with a button just continuously toggling the signal on and off. We will assume the clock signal as an input—in practice, people implement it with special analog circuits that we won’t cover in this class.
Here is some terminology about clocks:
- The clock is high when the value is 1 and low when the value is 0.
- Accordingly, a rising edge is the moment when the clock goes from low to high. A falling edge is when it goes from high to low. It can help to visualize these moments in a timing diagram, with real time on the x-axis and the clock value on the y-axis.
- The clock period is the time between two adjacent rising edges (or between two falling edges—it’s the same). So during one clock period, the clock is high for half the time and low for half the time. The period is measured in real time, i.e., in seconds.
- The clock frequency is the reciprocal of the clock period. It’s measured in hertz (Hz).
For examples of the latter two, one nanosecond is one billionth of a second. So a system with clock period 1 ns has a frequency of 1 GHz.
SR Latch
Let’s build our first stateful circuit. It’s called an SR latch, named after its two inputs: S for “set” and R for “reset.” It has one output, traditionally named Q.
The circuit is made of two NOR gates. Most of it will look familiar, but there’s one tricky aspect: one gate feeds back into itself, via the other gate. (See the visual notes associated with this lecture for the circuit diagram.)
Let’s attempt to analyze this circuit by thinking through its truth table:
| S | R | Q |
|---|---|---|
| 0 | 0 | |
| 0 | 1 | |
| 1 | 0 | |
| 1 | 1 |
The middle two rows are not too hard. When only one of S and R are 1, the NOR gates seem to “ignore” the feedback path. We can fill in those rows by propagating the signals through the wires:
| S | R | Q |
|---|---|---|
| 0 | 0 | |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 |
Now let’s try the first row, where both S and R are 0. The “feedback” path seems to actually matter in this case. One way to analyze the circuit is to assume the value for Q and then try to confirm. If you try this for both possible values of Q, something strange happens: we can “confirm” either assumption! It turns out that this circuit preserves the old value of Q. So while we’re definitely violating the rules of truth tables (so this is not really a truth table anymore), we can record a note about what happens here:
| S | R | Q |
|---|---|---|
| 0 | 0 | keep the old value |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 |
Finally, there’s the last case: where both S and R are 1. I would actually like to avoid talking too much about this case because it’s not part of the “spec” of what we want out of an SR latch. Now is a good time to talk about that spec—here’s how it’s supposed to behave:
- When S is 1, that’s a set, and we set the stored value to 1.
- When R is 1, that’s a reset, and we set the stored value to 0.
- Otherwise, when the circuit is “at rest” and their input is 1, the value stays what it was, and Q outputs the stored value.
- Please don’t set S and R to 1 simultaneously.
The annoying thing about it the “both 1” case is that, after you do this, you probably want to lower both inputs to 0 (to return to the “at rest” state). But the final value of Q depends on the (real time) order that these signals change, which is weird. So the “spec” for SR latches usually just says “please don’t do this.” It’s a little bit like undefined behavior!
D Latch
The SR latch, while an amazing first attempt at putting state into circuits, has two shortcomings, both of which stem from having separate S and R inputs:
- It’s kind of weird that there are two different wires for encoding the state that we want to store. Can’t we just have one, that is 0 when we want to store 0 and 1 when we want to store 1?
- There’s the uncomfortable business of the case where both S and R are 1 simultaneously. Can we prevent this?
We will now build a more sophisticated stateful circuit that solves both problems. It’s called a D latch. The key idea is to have a single data input (named D) that is 0 when we want to store 0 and 1 when we want to store 1. However, we also need a way to tell the circuit whether we are currently trying to store something, or whether the value should just stay the same. For that, we’ll wire up a clock signal (named C), and use the convention that the data can only get stored when the clock is high.
You can make a D latch by adding a couple of AND gates and an inverter “in front” of an SR latch. (Again, see the visual notes accompanying this lecture for the diagram.) It is useful to think again about the not-quite-truth-table for the circuit:
| C | D | Q |
|---|---|---|
| 0 | 0 | |
| 0 | 1 | |
| 1 | 0 | |
| 1 | 1 |
When C is 0 (the clock is low), notice that both AND gates are inactive, in the sense that they ignore their other input and output zero. So regardless of the value of D, both the S and R inputs to the SR latch are zero. That’s the case where the SR latch keeps its current value. So, in our table for the D latch, the same thing happens to Q:
| C | D | Q |
|---|---|---|
| 0 | 0 | keep |
| 0 | 1 | keep |
| 1 | 0 | |
| 1 | 1 |
Now let’s think about the rows where the clock is high. Now, one input to both AND gates is 1, so their output behaves like the other input (remember that b∧1=b for any bit b).
So what’s going on with those other inputs to the ANDs? D goes straight into the S input of the SR latch, and it is inverted when it goes into the R input. So in this setting, S and R are always opposites of each other: either S is 1 or R is one but not both. (Which is great, because we avoid the weird both-are-1 case.) The consequence is that:
- When D is 1, we set the SR latch.
- When D is 0, we reset the SR latch.
So let’s complete our not-quite-truth-table:
| C | D | Q |
|---|---|---|
| 0 | 0 | keep |
| 0 | 1 | keep |
| 1 | 0 | 0 (and store 0) |
| 1 | 1 | 1 (and store 1) |
The parentheticals there are meant to convey that we update the state that this circuit stores. So you can also think of the D latch’s “spec” this way:
- Q is always the current stored value.
- When the clock is low, ignore D and keep the current stored value.
- When the clock is high, store D and immediately start outputting it via Q.
D Flip-Flop
The D latch has simplified the interface quite a bit, but it still has a shortcoming that we’d like to fix. In complex circuits, it can be inconvenient that the Q output changes immediately with the D input. The problem is that, in the real world, circuits can take (real) time to determine the value of D that they want to store—and, during that time, the value of the D input might change. We would like to hide those transient changes and define a specific moment where we capture and store the value of D. That’s what our next circuit will do.
The idea is to only pay attention to D in the moment where the clock signal changes: the rising edge or the falling edge. We’ll use the rising edge, but the technique easily generalizes to using the falling edge. We want our new circuit, called a D flip-flop, to keep Q stable for entire clock periods, and to only change its value (to match the D input) at the moment of the rising clock edge.
You can make a D flip-flop by wiring up two D latches in series and inverting the first one’s C input. (Again, see the wiring diagram in the accompanying visual notes.) The way to analyze this circuit is to realize that only one of the two D latches is “awake” at a given time. The first is active when the clock is low, and the second is active when the clock is high. So it takes half the clock period for the new data value to make it halfway through the circuit, and the entire clock period to finally reach the Q output.
The D flip-flop is the fundamental building block for stateful circuits that we will use in this class.
Register
A register is the computer-science name for when you write up n flip-flops in parallel and treat them a single unit that can store n bits. When you use 32 of these together, all wired up to the same clock signal, we’ll call that as a 32-bit register.
Abstractly speaking, you can think of a register as behaving the same way as a D flip-flop, but storing an n-bit number instead of a single bit. That is, think of the register as having two inputs (a 1-bit clock signal and an n-bit data signal) and one output (also n bits); the register captures a new stored value on the rising edge of the clock and keeps its output stable for the entire following clock period.
Processors
So far, we have used the raw materials of switches to build circuits that can do arithmetic and store state. Now it’s time to go the rest of the way and build a computer.
Data Path
Let’s build something gradually more computer-like, step by step. (This evolution is necessarily somewhat visual, so please follow along with the diagrams posted elsewhere.) I think it’s interesting to ask yourself a philosophical question: what is a “computer”? It’s clearly a subjective definitional question, so you can decide for yourself.
- Start with an adder. You feed in two operands, and you get a result (the sum). Is this a computer? My personal opinion is no; it seems too fixed-function and too ephemeral.
- Let’s add two registers for the operands, and feed the adder’s output into both registers. Registers have an enable input that decides whether they take a new input. Now, let’s think about what the “user interface” is to this circuit: instead of two input numbers, it’s the two enable bits. By setting these bits, the user can decide to put the sum of the current register values back into either register (or both at once). This feels slightly more computer-like to me, because we are sequencing a few summations by setting those bits. But it is uncomfortably unrealistic that we have to input data by “reaching in” to the registers to set values.
- Next, we’ll add an immediate input to the user interface: a number that we can transfer directly into a register. We will need multiplexers in front of each register to decide whether to take the new value from the sum or the immediate input. The select bits for these multiplexers become part of the user interface too. This seems more “computery” to me, because we can do a whole sequence of sums just be interacting via the external interface.
Instruction
At the final step, we have created an interesting situation where the external interface constitutes an “instruction” for the circuit. Let’s say our numbers (registers and immediate) are all 4 bits. The interfaces has 8 bits total:
- An enable bit for each of the two registers, which decides whether we’re putting a new value into each.
- A select bit for each register, which decides whether that new value comes from the immediate input or the sum (the adder’s output). We’ll assume a convention where 1 means the immediate and 0 means the sum.
- Four immediate bits.
These are all just bits, so we can string them together into an 8-bit number. Let’s lay them out like this:
esesiiii
AABB
What I mean by this is: the most significant bit is the register A’s enable, the next is register A’s select, then there are B’s analogous bits, and then the last 4 bits are the immediate value. So let’s think about this instruction:
11001000
This instruction disables register B, it enables register A to take its value from the immediate. The immediate value is 10002=810. To summarize, this instruction says “set register A to 8.”
This is interesting!
We have created a situation where a plain ol’ number—just a string of bits—means something to our circuit.
To emphasize, you could also write this instruction as the hex number c8.
And this number means “set register A to 8.”
Machine Code
In a weird way, this view means we’ve defined a programming language. A really bad, primitive programming language. So a program like this:
c8
33
80
20
This program would execute these steps:
- Set A to 8.
- Set B to 3.
- Set A to the sum of A and B.
- Set B to the sum of A and B.
We’re kind of programming! In an extremely inconvenient way!
This bit-level “programming language” exists in every processor in existence. It is called machine code, and it is how all software on the computer works. Every program you’ve ever run, and every program you’ve ever written in every language, eventually translates down to machine code for your processor.
Instruction Set Architectures
A machine code language is called an instruction set architecture (ISA). We have, in this lecture, invented a little ISA. Let’s call this the femtoprocessor (FemtoProc) ISA, just to have a name, because this is for an extraordinarily tiny processor.
Some popular ISAs for “real” computers include:
- [RISC-V][], which we are using in this course.
- ARM, which your phone almost certainly uses and your laptop might use.
- Intel’s x86, which your laptop might use.
Each of these ISAs defines a “meaning” for strings of bits. Then, processors interpret those bits to decide which actions to take.
Assembly Language
Writing out the raw bits (or the hex numbers) can be really annoying. To make machine-code programs easier to write, ISAs typically come with a text format with a roughly 1-1 correspondence to machine code. For example, we can define an assembly language for FemtoProc consisting of two kinds of instructions:
wrimm {A,B}, N: Set the indicated register to the immediate value N.add {A,B}: Add the current values in registers A and B together, and put the sum into the indicated register.
Using these mnemonics, here’s our program above again in assembly language:
wrimm A, 8
wrimm B, 3
add A
add B
This already looks a little more like a programming language. Maybe you can imagine that it would be pretty easy to write a translator that takes this text format and turns it into actual machine-code bits in the FemtoProc ISA.
A tool that does this translation, from assembly language to machine code, is called an assembler.
Finishing the FemtoProc
Our FemtoProc data path is pretty cool, but we still have to tell it to run one instruction at a time. Real processors can run through an entire list of instructions autonomously.
To make this work, we need to add a few things:
- An instruction memory, which holds the bits for a series of instructions.
- A program counter (PC), which is a little register that holds the address of the current instruction.
- An incrementor, which is just an adder wired up to a constant value like 1 or 4, that increments the PC value on every cycle.
With this setup, the PC counts upward, cycle by cycle, and pulls a new instruction out of the instruction memory each time. This is the magic we need to get the “automatic sequencing” we wanted.
From FemtoProc to a Full Processor
Personally, I think this complete FemtoProc counts as a computer: the smallest, simplest viable computer, but a computer nonetheless.
“Real” processors, however, have a few additional elements that FemtoProc lacks:
- A register file, i.e., more than 2 registers. For example RISC-V defines 32 registers. Real ISAs pick these registers with binary numbers, not one enable bit per register.
- An arithmetic logic unit (ALU), which supports more than just adding: it can choose between adding, multiplying, shifting, etc.
- Some external data memory, which tracks a lot of data. The processor can load and store data from this memory.
The RISC-V ISA
Via our “bottom-up” trajectory, we built up from logic gates to the two-instruction FemtoProc. We will now take a leap to a full-featured processor and a standard, popular ISA: RISC-V.
Like FemtoProc’s ISA (and any ISA), RISC-V is an extremely primitive programming language made of bits, and it has a textual assembly format that makes it easier to read and write than entering binary values manually. Each instruction is like an extremely simple statement in a different programming language, and it describes a single small action that the processor can take.
Unlike FemtoProc, it has many more than two instructions—it has enough so that arbitrary C programs be translated to RISC-V code.
In fact, that’s what happened every time you have typed gcc during this whole semester.
Why Learn Assembly Programming?
Understanding assembly is important because it is the language that the computer actually speaks. So while it would be infeasible in the modern age to write entire large software projects entirely in assembly, it remains relevant for the small handful of exceptional cases where higher levels of abstraction obscure important information. Here are some examples:
- People hand-write assembly for extremely performance-sensitive loops. A classic example is audio/video encoding/decoding: the popular FFmpeg library, for example, is mostly written in C but contains hand-written RISC-V assembly for performance-critical functions. While modern compiler optimizations are amazing, humans can still sometimes beat them.
- Operating system internals typically need some platform-specific assembly to deal with the edge cases that arise with controlling user processes.
- Code that must be secure, such as encryption and decryption routines, are often written directly in assembly to avoid timing channels. If an encryption routine takes different amounts of time depending on the key, an attacker can learn the key by repeatedly measuring the time taken to encrypt or decrypt. By taking direct control over which instructions get executed, humans can sometimes ensure that the code takes a constant amount of time, so that the attacker can’t learn anything by timing it. This is hard to do by writing C because the compiler tries to be clever: by optimizing your code, it can “accidentally” make its timing input-dependent.
- Even more commonly: reading assembly is an important diagnostic skill. When something goes wrong, sometimes reading the assembly is the only way to track down the root cause. If it’s a performance problem, for example, understanding the source code only gets you so far. If it’s a compiler bug (and compilers do have bugs!), then debugging is hopeless unless you can read assembly.
For these reasons and others, it is important to know how to read and write assembly code. We will program in RISC-V during this semester, but the skills you learn as a RISC-V programmer will translate to other ISAs such as ARM and x86.
Recap: Assembly Principles
First, recall some programs we wrote in our two-instruction FemtoProc ISA, like this:
wrimm A, 8
wrimm B, 3
add A
add B
The important thing to keep in mind is that there are two ways of thinking about each assembly program: it is either a shorthand for machine code, or it is a programming language. The first interpretation says that each line is a mnemonic for some bits that control how the processor works. The second says you can forget about the processor and pay attention only to the ISA manual.
Under the first interpretation, remember that each FemtoProc instruction was 8 bits, so we can also represent this program as a string of binary numbers.
There is a 1-1 correspondence between lines in our assembly program and 1-byte instructions in the machine code.
In hex: c8 33 80 20.
Sometimes, it is helpful to see both the text form and the hex representation of the bytes side by side, like this:
c8 wrimm A, 8
33 wrimm B, 3
80 add A
20 add B
Under the second interpretation, we just want to understand what this program computes. My #1 recommendation for understanding assembly code is to translate it into pseudocode first and then read it. For example, we can translate our example line by line into pseudo-Python:
a = 8
b = 3
a = a + b
b = a + b
where the a and b variables correspond to the two FemtoProc registers.
To understand what this program actually does, we can try simplifying the Python code:
a = 8
b = 3
a = 8 + 3
b = 11 + b
So we know that this program puts 8+3=11 into register A and 11+3=14 into register B.
Let’s See Some RISC-V Assembly
To get started, let’s look at some RISC-V assembly code.
I mentioned already that, every time you have typed gcc so far this semester, you have been invoking a compiler whose job it is to translate your C into machine code.
We can ask it to instead stop at the assembly and print that out using the -S command-line flag.
Let’s start with an extremely simple C program:
unsigned long mean(unsigned long x, unsigned long y) {
return (x + y) / 2;
}
To see the assembly code, try a command like this:
$ rv gcc -O1 -S mean.c -o mean.s
The -S tells GCC to emit assembly, and -o mean.s determines the output file.
I’m also using some optimizations, with -O1, that clean up the code somewhat (in addition to making the code faster, it also makes the assembly more readable).
This is just a text file, so you can open it in the same editor you use to write C code.
Try opening it up.
There’s a lot going on in this output, but let’s zoom in on these 3 lines:
add a0,a0,a1
srli a0,a0,1
ret
This is a sequence of 3 assembly instructions. Just like in our FemtoProc ISA, each one works like a statement in a “real” programming language, and it describes a single, small action for the program to take. Even though we don’t know what these instructions do, we can puzzle through what this code does:
addprobably adds two numbers together. Which is good, because that’s what our original C program does first.srliis a little more mysterious. It turns out that this mnemonic stands for shift right logical immediate. The important part is that this is a bitwise right shift. So the compiler has cleverly decided to use something like>> 1instead of/ 2.retreturns from the function.
The takeaway here is that our “second interpretation” of assembly code works for RISC-V too. We can think of it as an extremely primitive programming language and understand the code that way, forgetting about the fact that each instruction corresponds to some control bits that orchestrate the circuitry in a processor.
A Look at the Bits
Now let’s return to the first interpretation of assembly code: it’s a roughly 1-1 reflection of the (binary) machine code for a program that actually executes. Let’s look at those bits.
Object Files and Disassembly
We can translate our .s assembly code into machine by assembling it.
Try this command:
$ rv gcc -c mean.s -o mean.o
The -c flag instructs GCC to just compile the code to an object file (with the .o extension), and not to link the result into an executable.
(You can also ask GCC to go all the way from C to a .o in one step if you want; just provide the .c file as the input and remember to use -c.)
You could look directly at this object file with xxd mean.o if you want, but that’s not very informative.
It’s more useful to disassemble the code in this file so you can see the text form of the instructions.
(Disassembling is the opposite of assembling: it’s a translation from machine code back to assembly code.)
Our container comes with a tool called objdump that can do this:
$ rv objdump -d mean.o
The important part of the output is:
0000000000000000 <mean>:
0: 00b50533 add a0,a0,a1
4: 00155513 srli a0,a0,0x1
8: 00008067 ret
Here’s how to read this output:
function address <function name>:
addr: machine code assembly instruction
On the right, we see the same three instructions in the textual assembly format.
On the left the tool is also printing out the hex form of the machine code (and the corresponding address).
For example, the first instruction consists of the bytes 00b50533, starting at address 0.
In RISC-V, every instruction is exactly 4 bytes long, so the next instruction starts at address 4.
Raw Machine Code
The .o object files that our compiler produces don’t just contain machine code; they also contain other metadata to make linking possible.
Sometimes (like on this week’s assignment), it is useful to have a “raw” binary file just containing the instructions.
In the CS 3410 container, we have provided a convenient command that makes it easy to produce these raw files, called asbin.
Let’s put just the instructions we want into a new file:
add a0, a0, a1
srli a0, a0, 1
ret
Try this command:
$ rv asbin mean.s
Then take a look at the bytes:
$ xxd mean.bin
00000000: 3305 b500 1355 1500 6780 0000 3....U..g...
You can see the bits for same 4-byte instructions here, with a twist. The bytes are backward, for a reason we’ll explain next (named endianness).
For the curious only: our little asbin script just runs a couple of commands.
You can run them yourself too:
$ as something.s -o something.o
$ objcopy something.o -O binary something.bin
The objcopy command is a powerful tool for converting between binary file formats, but we just need it to do this one thing.
We just thought this was common enough in CS 3410 that it would be handy to have a single command to do it all.
Endianness
The reason the instruction bytes appear backward in the file is because of a concept called endianness or byte order.
Different computers have different conventions for how to order the bytes within a multi-byte value.
For example, in RISC-V, both int and instructions are 4 bytes—which order should we put those bytes into memory?
The options are:
- Big endian: The “obvious” order. The most-significant byte goes at the lowest address.
- Little endian: The other order. The least-significant byte goes at the lowest address.
Fortunately or unfortunately, most modern computers use little endian.
That includes all of x86, ARM, and RISC-V (in their most common modes).
That’s why the lowest byte in our instructions appears first when we look at the binary file with xxd.
File I/O routines will hide this different from you, so if you read an int from a file, it will put the bytes in the right order by the time your program sees the bytes.
Why are these called big and little “endian”? It’s one of the all-time great examples of computer scientists being terrible at naming things: these names come from the 1726 novel Gulliver’s Travels by Jonathan Swift, from a part about a war between people who believe you should crack an egg on the big end or the little end.
RISC-V Assembly Basics
Let’s cover a few fundamental concepts that RISC-V will use for every instruction. We will break down this instruction from our example:
add a0, a0, a1
Registers
There are 32 registers.
RISC-V names them x0 through x31.
We’re using the 64-bit version of the RISC-V ISA, so each register holds a 64-bit value.
Alternative Names for Registers
While all the registers just hold bits, there are conventions about how each one is usually used. To help remind you of these purposes, RISC-V also gives the instructions alternative symbolic names. Wikipedia has a detailed table with all of these names that I won’t reproduce here. Here are some register names that will be relevant immediately:
x0is also known aszero. It is unique among all RISC-V registers because it cannot be written: it always holds the all-0s value. If you try to update this register, the write is ignored. Having quick access to “64 zeroes” turns out to be useful for many programs.x10throughx17are also known asa0througha7.x5,x6,x7, andx28throughx31are also known ast0throught6.x8,x9, andx18throughx27are also known ass0throughs11.
The latter 3 sets of registers (aN, tN, and sN) have subtly different conventions that have to do with function calls, which we’ll cover later.
For now, however, you can think of them as interchangeable places to put values when we’re operating on them.
You absolutely do not need to memorize the alternative names for every register—you just need to know that there are multiple names.
This way, you know that our instruction above is exactly equivalent to:
add x10, x10, x11
…because it just uses different names for the same registers. These alternate names are just an assembly language phenomenon (i.e., for human readability), and the machine code for these two versions looks exactly the same.
Three-Operand Form
Most RISC-V instructions take three operands, so they look like this:
<name> <operand>, <operand>, <operand>
The name tells us what operation the instruction should do, and the three operands tell us what values it will operate on.
So our example is an add instruction, with three register operands: a0, a0, and a1.
In these three-operand instructions, the first one is the destination register and the second two are the source registers.
You’ll sometimes see the format off the add instruction written like this:
add rd, rs1, rs2
The mnemonic is that r* are register operands,
d means destination,
and s means source.
So our instruction add a0, a0, a1 adds the values in a0 and a1 and puts the result in a0.
It is allowed, and extremely common, for the same register to be used both as a source and a destination.
Using the Manual
Working with assembly code entails reading the manual. A lot. In other languages, you can quickly build up an intuition for what all the basic components mean. In assembly languages, there are usually so many instructions that you need to look them up continuously. Expect to work with assembly with your code in one hand and the ISA manual in the other.
Navigate to this site’s RISC-V Assembly resource page. I recommend using the RISC-V reference card linked there all the time. In rare circumstances where you need more details, you can use the (very long) specification document. I’ll refer to the reference card here.
The first page of the reference card tells us what each instruction means.
To understand our add instruction, we can find it on the list to see the format, a short English description, and a somewhat cryptic pseudocode description of the semantics.
The second page tells us how to encode the instruction as actual machine-code bits. We’ll cover the encoding strategy next.
Instruction Encodings
Every assembly instruction corresponds to a 32-bit value. This correspondence is called the instruction encoding.
For example, we know that the add instruction we’re working with, when assembled, encodes to the value 0x00b50533.
Why those particular bits?
In RISC-V, instruction encodings use one of a few different formats, which it calls “types.” You can see a list of all the formats on the second page of the reference card: R-, I-, S-, B-, U-, and J-type (another list that you should not attempt to memorize). Each format comes with a little diagram mapping out the purpose of each bit in the 32-bit range.
Add Instruction
add is an R-type instruction (so named because all the operands are registers).
Reading from the least-significant to most-significant bits, the map of the bits in an R-type instruction consists of:
- 7 bits for the opcode. The opcode determines which instruction this is. The reference card tells us that the opcode for
addis 0110011, in binary. - 5 bits for rd, the destination register. It makes sense that the register is 5 bits because there are a total of 25=32 possible registers. So to use destination register
x10, we’d put the binary value 01010 into this field. - 3 function bits. (We’ll come back to this in a moment.)
- The first source register operand, rs1. Also 5 bits.
- The second source register, rs2. 5 bits again.
- 7 more function bits.
In RISC-V, the function bit fields—labeled funct3 and funct7—specify more about how the instruction should work.
They’re kind of a supplement to the opcode.
For example, the table tells us that add and sub (and many others) actually share an opcode, and the bits in funct3 and funct7 tell us which operation to perform.
To encode an add, set all the bits are zero.
So now we can describe exactly how to encode our example instruction, add x10, x10, x11.
Again starting with the least-significant bits:
- The opcode (7 bits): 0110011.
- rd (5 bits): decimal 10, binary 01010.
- funct3 (3 bits): 000.
- rs1 (5 bits): decimal 10, binary 01010 (again).
- rs2 (5 bits): decimal 11, binary 01011.
- funct7 (7 bits): 0000000.
Try stringing these bits together and converting to hex.
You should get the hex value the assembler produced for us, 0x00b50533.
Some handy tools for doing these conversions include:
- Bitwise, an interactive tool that runs in your terminal for experimenting with data encodings.
- The macOS Calculator app. Press ⌘3 to switch to “programmer mode.”
Add-Immediate Instruction
To try another format, consider this instruction:
addi a0, a1, 42
This add-immediate instruction is different from add because one of the operands isn’t a register, it’s an immediate integer.
The reference card tells us that this instruction uses a different format: I-type (the I is for immediate).
The distinguishing feature in this format is that the most-significant 11 bits are used for this immediate value.
(This field replaces the funct7 and rs2 fields from the R-type format.)
If we assemble this instruction, we get the 32-bit value 0x02a58513.
The interesting part is the top 12 bits, which are 00000010 1010 or, in decimal, 42.
Let’s Write an Assembly Program
Let’s try out our new reading-the-manual skills to write an assembly program from scratch.
Our program will compute (34−13)×2.
We’ll implement the multiplication with a left shift, so our program will work like the C expression (34 - 13) << 1.
When writing assembly, it can help to start by writing out some pseudocode where each statement is roughly the complexity of an instruction and all the variables are named like registers. Here’s a Python-like reformatting of that expression:
a0 = 34
a1 = a0 - 13
a2 = a1 << 1
I’ve used three different registers just for illustrative purposes; we could definitely have just reused a0.
Let’s translate this program to assembly one line at a time:
- We need to put the constant value 34 into register
a0. Remember the add-immediate instruction? And remember the specialx0register that is always zero? We can combine these to do something likea0 = 0 + 34, which works just as well. The instruction isaddi a0, x0, 34. - Now we need to subtract 13.
Let’s look at the reference card.
There is no subtract-immediate instruction… but we can add a negative number.
Let’s try the instruction
addi a1, a0, -13. - Finally, let’s look for a left-shift instruction in the reference card.
We can find
slli, for shift left logical immediate. The final instruction we need isslli a2, a1, 1.
Here’s our complete program:
addi a0, x0, 34
addi a1, a0, -13
slli a2, a1, 1
To try this out, we could compile it to machine code, but this would be a little hard to work with because we’d need to craft the assembly code to print stuff out.
(We’ll cover more about how to do this over the coming weeks.)
Instead, a handy resource that you can find linked from our RISC-V assembly resources page is this online RISC-V simulator.
Try pasting this program into the web interface and clicking the “Run” or “Step” buttons to see if we got it right:
i.e., that the program puts the result (34−13)×2 into register a2.
CPU Architecture
The 5 Classic CPU Stages
If we return to our processor schematic, we can break down all the things that a CPU needs to do for every instruction. These responsibilities are called stages:
- Fetch the instruction from the instruction memory.
- Decode the instruction bits, producing control signals to orchestrate the rest of the processor. Read the operand values from the register file. For example, this stage needs to convert from a binary encoding of each register index into a “one-hot” signal to read from the appropriate register.
- EXecute the actual computation for the instruction, using the arithmetic logic unit (ALU): add the numbers, shift the values, whatever the instruction requires.
- Access Memory, reading or writing an address in the external data memory. Only some instructions need this stage—just loads and stores.
- Write results back into the register file. The result could come from the ALU or from memory, if it’s a load instruction.
As the bolding in this list implies, computer architects often abbreviate these stages with a single letter: F, D, X, M, or W.
Architecture Styles
To design a processor, we have to decide how to map these stages for each instruction onto clock cycles.
One basic trade-off at work here is that we could do more work in a given cycle, but this inevitably makes the clock period longer. There is no “free lunch” available by breaking the work up across multiple cycles. However, doing this does open up an opportunity for a secondary optimization.
There are three main architecture styles:
-
Single-cycle processor. This is the most obvious approach: do all the work for a single instruction in one cycle. Because it’s a lot of work, the clock period is long, but you can execute n instructions in n cycles.
-
Multi-cycle processor. Do just one stage per cycle. If we use the 5 stages above, now every instruction takes 5 cycles to execute—but those cycles can be much shorter than for a single-cycle processor. A multi-cycle processor requires adding registers to hold signals between cycles.
-
Pipelined processor. If you build a multi-cycle processor, you quickly notice that much of your circuit remains idle most of the time. For example, the part of the processor for the Fetch stage is only active every 5th cycle. We can exploit that idle time!
The idea is to overlap the executions of different instructions. While we Decode one instruction, we can simultaneously Fetch the next instruction. If everything overlaps perfectly in a 5-stage pipeline, it takes only 4+n cycles to execute n instructions. And the clock period can be nearly as fast as for a multi-cycle processor.
Pipelining is such a useful idea that the vast majority of real processors use it. Real processors actually tend to break instruction processing into many more than 5 stages. It’s difficult to find public information about the specifics, but, as one data point, this reliable source claims that an oldish Intel processor had somewhere between 14 and 19 stages.
Load & Store Instructions
The Memory Hierarchy
So far, we have seen a bunch of RISC-V instructions that access the 32 registers, but we haven’t accessed memory yet. Registers are fine as long as your data fits in 31 64-bit values, but real software needs “bulk” storage, and that’s what memory is for.
In general, computer architects think of these different ways of storing data as tiers in an organization called the memory hierarchy. You can imagine an entire spectrum of different ways of storing data, all of which trade off between different goals:
- Smaller memories that are closer to the processor and faster to access.
- Larger memories that are farther from the processor and slower to access.
Registers are toward the first extreme: in 64-bit RISC-V, there is only a total of 31×8=248 bytes of mutable storage, and it usually takes around 1 cycle (less than a nanosecond) to access a register.
Modern main memory is at the opposite extreme: even cheap phones have several gigabytes of main memory, and it typically takes hundreds of of cycles to access it.
You might reasonably ask: why not make the whole plane out of registers? There are two big answers to this question.
- In real computers, these different memories are made out of different memory technologies. The physical details of how to construct memories are out of scope for CS 3410, but registers are universally made from transistors (like the flip-flops we built in class) and integrated with the processor, main memory is made of DRAM, a memory-specific technology that uses tiny little capacitors to store bits. DRAM requires different manufacturing processes than logic, is much cheaper per bit than integrated-with-logic storage, but it is also much slower.
- There is a fundamental trade-off between capacity and latency. In any memory technology you can think of, building a larger memory makes it take longer to access.
Registers and main memory are two points in the memory-hierarchy spectrum. There are other points too: later in the semester, we will learn much more about caches, which fill in the space in between registers and main memory. You can also think of persistent storage (magnetic hard drives or flash memory SSDs) or even the Internet as further tiers beyond main memory.
Extension and Truncation
When we access memory, we will often need to change the size (the number of bits) of various values. For example, we’ll need to take an 8-bit value and treat it as a 64-bit value, and we’ll need to take a 64-bit value and treat it as a 32-bit value. When you increase the number of bits, that’s called extension, and when you decrease the size, that’s called truncation. The goal in both situations is to avoid losing information whenever possible: that is, to keep the same represented integer value when converting between sizes.
Truncation
Truncation from m bits to n bits works by extracting the lowest (least significant) n bits from the value. There is, sadly, no way to avoid losing information in some cases. Here are some examples:
- Let’s truncate the 64-bit value
0x00000000000000abto 32 bits. In decimal, this number has the value 171. Truncating to 32 bits yields0x000000ab. That’s also 171. Awesome! - Let’s truncate
0xffffffffffffffabto 32 bits. That’s the value -85 in two’s complement. Truncating yields0xffffffab. That’s still -85. Excellent! - Now let’s truncate the bits
0x80000000000000ab(note the 8 in the most-significant hex digit). That’s a really big negative value, because the leading bit is 1. Truncating yields0x000000ab, which represents 171. That’s bad—we now have a different value. But losing some information is inevitable when you lose some bits.
Extension
There are two modes for extending from m bits to n bits. Both work by putting the value in the m least-significant bits of the n-bit output. The difference is in what we do with the extra n−m bits, which are the most-significant (upper) bits in the output.
- Zero extension fills the upper bits with zeroes.
- Sign extension fills them with copies of the most-significant bit in the input. (That is, the sign bit.)
Let’s see some examples.
- Let’s zero-extend
0xffffffab(remember, that’s -85) to 64 bits. The result is0x00000000ffffffaba pretty big positive number (4294967211 in decimal). So we didn’t preserve the value. - Now let’s sign-extend the same value.
Because the most significant bit in the 32-bit input is 1, we fill in the upper 32 bits with 1s.
The output is
0xffffffffffffffabin hex, or -85 in decimal. So we preserved the value!
The moral of the story is: when extending unsigned numbers, use zero extension; when extending signed numbers, use sign extension.
Load and Store Instructions
The 64-bit RISC-V instruction set gives you several instructions for loading from and storing to memory. They are very similar; the only difference is the size of the load or store: the number of bits we’re reading or writing.
Let’s start with ld and sd.
The mnemonics use l and s for load and store, and the d means double word, which means they load/store 64 bits at a time.
The format looks like this:
ld rd, offset(rs1)
sd rs2, offset(rs1)
In both cases, the second operand is the address.
This operand uses the funky-looking offset(rs1) syntax.
This means “get the value from register rs1, and add the constant value offset to it; treat the result as the address.”
The reason these instructions have a built-in constant offset is because it is so incredibly common for code to need to add a small constant value to an address before doing the access.
If you don’t need this offset, you can always use 0 for the offset.
The ld instruction puts the value into rd.
The sd instruction takes the value from rs2 and stores it to memory at the computed address.
Accessing Different Widths
The instruction set gives you several other load and store operations for different widths. Here is a non-exhaustive list:
ldandsd: Load or store a double word (64 bits).lw,lwu, andsw: Load or store a word (32 bits).lb,lbu, andsw: Load or store a byte (8 bits).
Recall that our registers are all 64 bits. So what happens when you use a smaller-width load or store?
- When storing, you truncate (take the lowest n bits from the register).
- When loading, you extend. The instruction tells you whether you zero-extend or sign-extend:
- The instructions with the
usuffix are for unsigned numbers, and they zero-extend. - The instructions without this suffix are for signed numbers, and they sign-extend.
- The instructions with the
So, for example, lb loads a single byte and sign-extends it to 64 bits to put it in a register.
lbu does the same thing, but it zero-extends instead.
Example: Store Word, Load Byte
Consider this short program:
addi x11, x0, 0x49C
sw x11, 0(x5)
lb x12, 0(x5)
What is the value of x12 at the end?
As always, it helps to translate the assembly to pseudocode to understand it. Here’s one attempt:
x11 = 0x49c;
store_word(x11, x5);
x12 = load_byte(x5);
So we don’t know what address x5 holds, but that’s the memory address.
We’re storing the value 0x49c as a word (32 bits) to that address,
and then loading the byte at that address.
Let’s look at the two steps:
- First, we store the 64-bit value
0x49c. Since we use little endian, least-significant byte goes at the smallest address. Let’s sayx5holds the address a. Then address a will hold the byte0x9c, a+1 holds the byte0x04, and addresses a+2 and a+3 both hold zero. - Next, we load the byte at the same address. The load instruction gets the byte
0x9c, and it sign-extends it to 64 bits, so the final value is0xffffffffffffff9c, or -100 in decimal if we interpret it as a signed number.
Example: Translating from C
How would you translate this C program to assembly?
void mystery(int* x, int* y) {
*x = *y;
}
Assume (as is the case on our RISC-V target) that int is a 32-bit type.
Assume also that the pointers x and y are stored in registers x3 and x5, respectively.
Here’s a reasonable translation:
lw x8, 0(x5)
sw x8, 0(x3)
Here are some salient observations about this code:
- It makes sense that this is a load instruction followed by a store instruction, because we need to read the value at
yand write it back to addressx. - It also makes sense that we are using word-sized accesses (
lwandsw) because that’s how you access 32 bits. - We use the signed version of the load (
lwinstead oflwu) to get sign-extension, not zero-extension. (If we usedunsigned intinstead, you would wantlwu.) - The offset is zero in both instructions, because we want to use the addresses in
x5andx3unmodified.
Control Flow in Assembly
So far, all the assembly programs we’ve written have been straight-line code, in the sense that they always run one instruction after the other.
That’s like writing C without any control flow: no if, for, while, etc.
This lecture is about the instructions that exist in RISC-V to implement control-flow constructs.
Branch If Equal
For most instructions, when the processor is done running that instruction, it proceeds onto the next instruction (incrementing the program counter by 4 on RISC-V, because every instruction is 4 bytes).
A branch instruction is one that can choose whether to do that or to execute some other instruction of your choosing instead.
One example is the beq instruction, which means branch if equal:
beq rs1, rs2, label
The first two operands are registers, and beq checks whether the values are equal.
The third operand is a label, which we’ll look closer at in a moment, but it refers to some other instruction.
Then:
- If the two registers hold equal values, then go to the instruction at
label. - If they’re not equal, then just go to the next instruction (add 4 to the PC) as usual.
Labels appear in your assembly code like this:
my_great_label:
That is, just pick a name and put a : after it.
This labels a specific instruction so that a branch can refer to it.
Here’s an example:
beq x1, x2, some_label
addi x3, x3, 42
some_label:
addi x3, x3, 27
This program checks whether x1 == x2.
If so, then it immediately executes the last instruction, skipping the second instruction.
Otherwise, it runs all 3 instructions in this listing in order (it adds 42 and then adds 27 to x3).
In other words, you can imagine this assembly code implementing an if statement in C:
if (x1 != x2) {
x3 += 42;
}
x3 += 27;
Other Branches and Jumps
You should read the RISC-V spec to see an exhaustive list of branch instructions it supports.
Here are a few, beyond beq:
bne rs1, rs2, label: Branch if the registers are not equal.blt rs1, rs2, label: Branch ifrs1is less thanrs2, treated as signed (two’s complement) integers.bge rs1, rs2, label: Like that, but with “greater than.”bltuandbgtuare similar but do unsigned integer comparisons.
You will also encounter unconditional jumps, written j label.
Unlike branches, j doesn’t check a condition; it always immediately transfers control to the label.
Implementing Loops
We have already seen how branches in assembly can implement the if control-flow construct.
There are also all you need to implement loops, like the for and while constructs in C.
We’ll see a worked example in this section.
Consider this loop that sums the values in an array:
int sum = 0;
for (int i = 0; i < 20; i++) {
sum += A[i];
}
And imagine that A is declared as an array of ints:
int A[20];
Imagine that the A base pointer is in x8.
Here’s a complete implementation of this loop in RISC-V assembly:
add x9, x8, x0 # x9 = &A[0]
add x10, x0, x0 # sum = 0
add x11, x0, x0 # i = 0
addi x13, x0, 20 # x13 = 20
Loop:
bge x11, x13, Done
lw x12, 0(x9) # x12 = A[i]
add x10, x10, x12 # sum += x12
addi x9, x9, 4 # &A[i+1]
addi x11, x11, 1 # i++
j Loop
Done:
The important instructions for implementing the loop are the bge (branch if greater than or equal to) and j (unconditional jump) instructions.
The former checks the loop condition i < 20, and the latter starts the next execution of the loop.
We have included comments to indicate how we implemented the various changes to variables. Here are some observations about this implementation:
- We have chosen to put
sumin registerx10andiinx11. - The
x13register just holds the number 20. We need it in a register so we can comparei < 20with thebgeinstruction. - The
x9register is a little funky. It starts out storing theAbase address, but then the pointer moves by 4 bytes on every loop iteration (withaddi). The idea is that it always stores the address&A[i], i.e., a pointer to the ith element of theAarray on the ith iteration. So to load the valueA[i], we just need to load this address withlw.
Logical Operations in RISC-V
RISC-V has a full complement of instructions to do bitwise logical operations.
Remember using &, |, <<, and >> for masking and combining in bit packing code?
These instructions implement those C-level constructs.
Basic Logic
To start with:
- Bitwise and:
and,andi - Bitwise or:
or,ori - Bitwise exclusive or (xor):
xor,xori
These are all three-operand instructions.
All of these instructions operate on all 64 bits in the registers at once.
They also all have a register version and an immediate version; the latter one has the i suffix.
The forms of the instructions are like:
xor rd, rs1, rs2
xori rd, rs1, imm
So the first version takes two register inputs, while the second takes a register and an immediate.
What About Not?
There is no (real) bitwise “not” instruction.
The reason is that ~x is equivalent to x ^ -1, i.e., XORing the value with the all-ones value.
If you spend some quality time with the XOR truth table, you’ll notice that you can think of it this way:
- The first input to the XOR is a bunch of bits. You want to flip some of these bits.
- The second input contains 1s in all the places where you want to flip the bit in the first input. Where this input is zero, leave the other bits alone.
So XORing with an all-ones value means “flip all the bits.”
Instead of a proper “not” instruction, you can use xori:
xori rd, rs1, -1
In fact, RISC-V has made your life somewhat easier: it lets you write a pseudo-instruction to mean this.
So in assembly code, you can actually pretend there is a not instruction:
not rd, rs1
But there is no separate opcode for not; it is not a real instruction.
The assembler will translate the line of assembly above into an xori instruction for you.
Keeping the number of “real” instructions small—by eliminating needless instructions that can be easily implemented with other instructions—keeps processors small, simple, and efficient.
This is the reduced instruction set computer (RISC) philosophy.
Shifts
RISC-V has bit-shifting instructions to implement C’s << and >>.
Here are the ones for shifting left:
slli rd, rs1, imm: Shift left by an immediate amount.sll rd, rs1, rs2: Shift left by an amount in a register.
No surprises here. But for rightward shifts, RISC-V has twice as many versions:
srlandsrli: Shift right logical.srasrai: Shift right arithmetic.
What is the difference between an arithmetic and a logical shift? The difference is similar to the deal with sign extension and zero extension: the difference is in what you do with the most-significant n bits that weren’t there before. That is, if you shift right by n bits, you just drop the original value’s least significant n bits, but what should you put for the output value’s most significant n bits? The two versions differ in their answer:
- Logical shift right: Fill in those n most-significant bits with 0s.
- Arithmetic shift right: Fill them in with copies of the sign bit.
Say, for example, that you have a register containing the negative number -3410, in two’s complement.
- If you use
sraito do an arithmetic shift right, you fill in the top bit with a copy of the original number’s sign bit, which is a 1. So the result is still negative: -1705. - If you instead use
srlito do a logical shift right, the most-significant bit of the output will be a 0. So the result will be a very large positive number.
As with sign- and zero-extension, you want to use logical right shifts for unsigned numbers and arithmetic right shifts for signed numbers.
Consider asking yourself: why is there no separate arithmetic left shift?
An Example
Imagine that x10 contains the value 0x34ff.
What does x12 contain after you run these instructions?
slli x12, x10, 0x10
srli x12, x12, 0x08
and x12, x12, x10
Try working through the instructions one step at a time. It can save time to write the values in the registers in hex, if you can imagine the corresponding binary in your head.
The result value is 0x3400.
Calling Functions in Assembly
Pseudo-Instructions
While assembly languages mostly have a 1-1 correspondence to some processor’s machine code, sometimes it’s helpful for the assembly language to have a few convenient features that just make it easier for humans to read and write. The primary such feature in RISC-V assembly is its pseudo-instructions. A pseudo-instruction is an assembly-language instruction that does not actually correspond to any distinct machine-code instruction (with its own opcode and such).
Here are some common pseudo-instructions:
mv rd, rs1: Copy the value of registerrs1into registerrd.li rd, imm: Put the immediate valueimminto registerrd.nop: A no-op: do nothing at all.
All three of these pseudo-instructions are equivalent to special cases of the addi instructions:
mv rd, rs1does the same thing asaddi rd, rs1, 0li rd, immisaddi rd, x0, immnopisaddi x0, x0, 0
Try to convince yourself that these addi instructions do in fact work to implement these pseudo-instructions’ semantics.
The RISC-V assembler translates pseudo-instructions into their equivalent real instructions for you. So you can write li x11, 42 and that will translate to exactly the same machine-code bits as addi x11, x0, 42.
Why doesn’t RISC-V implement these pseudo-instructions as real, distinct instructions? By keeping the number of instructions small, it simplifies the hardware—especially the decode stage—making it smaller, faster, and more efficient.
Functions in Assembly
With branching control flow, we can accomplish a lot in RISC-V assembly.
We can “fake” if statements, for loops, and so on.
But one thing we can’t do yet is call functions.
That’s what this lecture is about.
Here’s an example C program we can work with:
int mult(int mcand, int mlier) {
int product = 0;
while (mlier > 0) {
product = product + mcand;
mlier = mlier - 1;
}
return product;
}
int main() {
int i, j, k, m;
// ...
i = mult(i, k);
m = mult(i, i);
// ...
}
You already know how to implement the body of the mult function in RISC-V.
But nothing we’ve done so far will let us call that code multiple times with different arguments, as main does in this example.
Calling a function is a multi-step process, and it requires collaboration between both the caller code and the callee code (the function being called). At a high level, every function call needs to follow these steps:
- The caller puts arguments in a place where the callee function can access them.
- The caller transfers control to the callee (i.e., it jumps to the first instruction in the function).
- The function creates a stack frame to hold its own local variables.
- The function actually does stuff: i.e., the function body.
- The function puts the return value in a place where caller can access it. It also restores any registers it used to the state the caller expects. And finally, it releases the stack frame that holds its local variables.
- The callee returns control to the caller (i.e., jumps to the next instruction in the caller right after the function call).
The caller and callee need to agree on all the details for how this multi-step process works. For example, they must agree on which registers hold the arguments and which registers hold the return value. A standardized protocol for how to implement all these details is called a calling convention. The RISC-V ISA itself defines a particular calling convention, which we will learn about in this lecture. C compilers that generate RISC-V code also use the same calling convention to implement function definitions and function calls—and because it’s standardized, even functions compiled by different C compilers can call each other.
The RISC-V Calling Convention
We’ll break down the components next, but here are the most important parts of the RISC-V calling convention:
- Arguments go in registers
a0througha7(a.k.a.x10throughx17). (In fact, that is why these registers have an alternative name starting with an “a”! It’s for argument.) - Return values also go in registers
a0anda1. (Yes, this means that functions overwrite their arguments with their return values before they return.) - Register
ra(a.k.a.x1) holds the return address: the address of the next instruction to run after the function call finishes. - Registers
s0throughs11(a.k.a.x8,x9, andx18throughx27) are callee-saved registers. This means that callers can safely expect that, after they make a call and the call returns, the registers will be carefully restored to the value they had before the call.
Control Flow for Call and Return
Let’s start with the basic mechanism for transferring control:
jumping from the caller to the callee and then back.
The interesting thing is that the [branch instructions we’ve seen so far][ctr], such as beq, won’t suffice.
The problem is that functions, by their very nature, can be called from multiple locations.
Like in our example above:
i = mult(i, k);
m = mult(i, i);
Imagine that we implemented both of these calls with a plain unconditional jump, j, like this.
Then the calls might look like this:
mv a0, <register containing i>;
mv a1, <register containing k>;
j mult;
mv <register containing i>, a0;
mv a0, <register containing i>;
mv a1, <register containing i>;
j mult;
mv <register containing m>, a0;
All those mv instructions would take care of setting up the argument registers and consuming the return-value register.
We imagine here that mult is an assembly-language label that points to the start of the mult function’s instructions.
There’s a problem.
In the implementation of the mult function, how do we know where to jump back to?
After each call is done, we need to transfer control to the next instruction after the jump.
Even if we inserted labels on those instructions, if there is only a single block of instructions to implement mult, those instructions would need to contain j <label> to return.
But somehow it would need to pick a different label for each call, which is impossible!
The solution is to designate a register to hold the return address for the call.
Instead of just using j to call a function, we’ll do two things:
- Record the next instruction’s address as the return address, in register
ra. - Jump to the first instruction of the called function.
Then, to return, the function just needs to jump to the instruction address in register ra.
Regardless of who called the function, doing this will suffice to transfer control to the point right after the call.
RISC-V has instructions to support these strategies: both the call and the return.
For the call, you use the jal instruction (the mnemonic stands for jump and link):
jal rd, label
The jal instruction does the two things we need for a call:
- Put the address of the next instruction after the
jalinto registerrd. - Unconditionally jump to
label.
So our function calls will generally look like jal ra, <function label>.
Then, to return from a function, we’ll use the jr instruction (the mnemonic means jump register):
jr rs1
The jr unconditionally jumps to the address stored in the register rs1.
So function returns generally look like jr ra.
In fact, this pattern is so common that RISC-V has pseudo-instructions for function calls and returns:
jal label: short forjal ra, labelcall label: like the above, but with an extraauipcinstruction so it supports larger PC offsetsret: short forjr ra
(Going one level deeper, it turns out that jr rs1 is itself a pseudo-instruction that is short for jalr x0, 0(rs1). But that’s not really important for learning about function calls.)
Managing the Stack
Beyond just jumping around, functions also have another important responsibility: they need to keep track of the their local variables. As you already know, local variables go in stack frames on the call stack. You also know that the stack is a region in memory grows downward (from higher memory addresses to lower ones) when we call functions, and it shrinks when function calls return. This section is about the bookkeeping that functions must to do create and use their stack frames.
The central idea is that we must use a register to keep track of the address of our current stack frame.
According to the RISC-V calling convention, register sp (a.k.a. x2) contains the address of the bottom (the smallest address) of the current stack frame.
Code interacts with sp in three main ways:
- At the beginning of the function, it will move
spdownward to make space for its own stack frame. Remember, this stack frame will contain the function’s local variables. - During the execution of the function, it will use (positive) offsets on
spto locate each of its local variables. So you’ll see stuff likeld a7, 16(sp)andsd a9, 40(sp)to load and store local variables using offsets fromsp. - At the end of the function, before it returns, it will move
spback up to wherever it used to be, “destroying” its stack frame. No memory literally gets destroyed, of course, but adjustingspback to its pre-call value indicates that we’re done using all our local variables, and it lets the caller locate its own stack frame.
This means that functions usually look like this:
func_label:
addi sp, sp, -8
...
addi sp, sp, 8
ret
The addi at the top and bottom of the function “creates” and “destroys” the stack frame.
The function’s code must know how big its stack frame needs to be:
in this case, it’s 8 bytes, so we move the stack pointer down by 8 bytes at the beginning and back up by the same 8 bytes at the end.
The stack frame size needs to be big enough to contain the function’s local variables;
C compilers compute this stack-frame size for you by adding up the size of all the local variables you declare.
Next
Notes TK:
- a more complete example of a leaf function
- saving & restoring ra & sp
- caller-/callee-saved registers
- an even more complete example of a function with a call
- recursive functions
Caches
The Memory Bottleneck
Remember our overview of computer architecture styles, where we assumed that each step in an instruction execution could happen in about one clock cycle? The assumption then was that it took about the same length of time to: fetch an instruction; decode it into control signals and access the register file; actually perform an arithmetic/logic operation like adding or multiplying two numbers; load or store to memory, if necessary; and write results back to the registers.
We can now tell you that this was a convenient fiction. While many of these stages do take about a cycle, there are important exceptions. For example, while it is easy to implement an integer addition circuit within one clock period (even at today’s multi-gigahertz clock frequencies), multiplication and division can often take several cycles. Think something like 3 to 15 cycles, depending on the complexity of the operation and the clock frequency.
But most importantly, accessing a computer’s memory is way slower than everything else. Loading or storing a single value to/from main memory takes hundreds of cycles on a modern computer. Because practical programs access memory every few instructions, this means that the performance of the memory system is an enormous factor in the performance of a computer system.
There are two big reasons why main memory is so slow: it is far away from the processor (both physically and metaphorically), and it uses a different physical technology. The result is that on-chip memory is fast, small, and expensive; off-chip (main) memory is slow, large, and cheap. For more on this fundamental trade-off, see our previous notes on the memory hierarchy.
SRAM vs. DRAM
One of the features of the memory hierarchy’s trade-off is a difference in manufacturing technology. Data storage on the CPU uses a technology called static RAM (SRAM), which is just built out of transistors—the same stuff that we make logic gates and registers out of. The ubiquitous technology for off-chip memory is dynamic RAM (DRAM). DRAM is a completely different technology that works by manufacturing arrays of tiny capacitors and periodically filling them with charge.
We already mentioned that SRAM is small, fast, and expensive while DRAM is large, slow, and cheap. But it’s worth dwelling for a moment on the sheer magnitude of the differences between the two.
- Speed: Accessing a value in SRAM typically takes roughly on the order of 0.5 nanoseconds. And in general, accessing any element in an SRAM is equally fast. In DRAM, accessing the first value in a DRAM array can take tens of nanoseconds. Subsequently accessing nearby values can be faster.
- Size: A typical size for an on-chip SRAM is roughly on the order of 1 MB. Even an entry-level laptop in 24 comes with 16 GB of DRAM.
- Cost: A rough estimate for the cost of DRAM storage is $3 per GB. It’s hard to pin down a good estimate for the cost of SRAM alone, because it usually comes with logic, but a good ballpark estimate is in the order of thousands of dollars per GB.
Because the trade-off is so extreme, it makes sense that computers would want to have some of each. An all-DRAM computer would be way too slow, and an all-SRAM computer would be way too expensive. Carefully combining memories of different speeds can have a huge impact on the cost/performance trade-off of a system.
Locality
This lecture is about caching, a technique that adds an intermediate-sized memory between registers and main memory. The idea is to build, out of SRAM, a place to put data that we access frequently. Then we’ll automatically transfer data from main memory (DRAM) to the cache (SRAM) so that most accesses, on average, can find their data in the cache.
To make this work, we will need a policy for automatically predicting which data is likely to be accessed frequently in the future. The key principle that caches will exploit is locality. Locality is a common pattern in real software that says that similar data is likely to be accessed close together in time.
Computer architects distinguish between two different forms of locality. Both of them are assumptions about how “normal” programs are likely to behave:
- Temporal locality: If a program accesses a given value, it is likely to need to access the same value again sometime soon.
- Spatial locality: If a program accesses a given value, it is likely to access nearby values in memory (i.e., addresses that are numerically close to the original address) sometime soon.
To illustrate the difference, consider this program:
int total = 0;
for (int i = 1; i < n; i++) {
total += a[i];
}
return total;
Let’s think about the accesses to total and a[i].
Do these accesses exhibit spatial or temporal locality?
- The accesses to
totalhas high temporal locality because we access the same variable (the same address in memory) on every iteration of the loop—i.e., separated by only a few instructions. - The
a[i]accesses have high spatial locality because we are repeatedly, and close by in time, accessing nearby addresses in memory. When the program loadsa[i], it will very soon ask loada[i+1], whose address is only 4 bytes away.
Locality is an extremely general principle. Maybe you can think a little bit about other situations in your life that seem to exhibit temporal or spatial locality. Common examples of mechanisms for exploiting locality in everyday life include refrigerators, backpacks, and laundry hampers.
Hits & Misses
The idea with a cache is to try to “intercept” most of a program’s memory accesses. A cache wants to fulfill as many loads and stores as it can directly, using its limited pool of fast SRAM. In rare conditions where it does not have the data already, it reluctantly forwards the request on to the larger, slower main memory.
In the presence of a cache, every memory access that a program executes is either a cache hit or a cache miss:
- A hit happens when the data already exists in the cache, so we can fulfill the request quickly.
- A miss is the other case: the data is not already in the cache, so we have to send the request on to DRAM.
A cache’s purpose in life is to maximize the hit rate (or, equivalently, minimize the miss rate).
A Hierarchy of Caches
A single cache is good, so multiple caches must be better! Remember, there is a fundamental trade-off between memory size and speed. So modern computers don’t just have one cache at a single point in this trade-off space; they use several different caches of different sizes (and therefore different speeds). These are layered into a hierarchy.
It is common for modern machines to have three levels of caching, called the L1, L2, and L3 caches. The L1 cache is closest to the processor, smallest, and fastest. It is not unheard of to tack on an L4 cache. There are diminishing returns eventually, so this doesn’t go on forever.
In the L1 cache, it is also common for computers to separate the data and the instructions into separate caches. The data and instructions coexist in main memory, so it is totally reasonable to have a single L1 cache for both. But it turns out that the locality patterns for accessing instructions and data are so different that, to maximize performance, computer architects have found it helpful to keep them separate. You will sometimes see these separate caches abbreviated as the L1I and L1D cache.
Direct-Mapped Cache
We have talked a lot about the goals of a cache; let’s finally talk about how caches work. We’ll start with a simple style of cache called a direct-mapped cache. In this kind of cache, every address in main memory is mapped to exactly one location in the cache.
Let’s say we have 64-bit memory addresses, and we have a cache that can store 2n≪264 values. To state the obvious, it is impossible for every memory address to get its own entry in the cache! So we need some policy to map memory locations onto cache locations. In a direct mapped cache, this is a many-to-one mapping.
Here’s the policy: we will split up the memory address, and we will use the least significant n bits of the address to determine the cache index, i.e., the location within the cache where this data will go. We have 2n cache locations, and there are 2n possible values of these n bits, so each value gets its own entry in the cache. We will then call the other 64−n bits the tag; we will need these to disambiguate which address a given cache entry is currently holding.
We’ll implement the hardware for our cache so that each of the entries has 3 values: the tag, a valid bit, and the actual data. Let’s visualize a tiny 4-entry (n=2) cache like this:
| index | valid? | tag | data |
|---|---|---|---|
| 00 | |||
| 01 | |||
| 10 | |||
| 11 |
Here’s what these columns mean:
- The index is literally just the index of the cache entry. (This never changes.)
- The valid bit indicates whether that cache entry currently holds meaningful data at all. 0 means invalid (“don’t pay attention to this at all; nothing to see here”) and 1 means valid (“I am currently holding some cached data”). The invalid state is useful at program startup, when the cache doesn’t hold anything at all (all entries are invalid).
- The tag bit is those other 64−n bits of the current value in the cache entry. That is, every cache entry could contain one one of 264−n different memory addresses; the tag tells us which one it currently is.
- The data is the current value at that memory address. (This is the raison d’être of the cache!)
Now, to access a memory address a, we’ll execute this algorithm:
- Split the address a into an index i (n bits) and a tag t (the other 64−n bits).
- Look in entry i of the cache.
- Is the entry valid (is the valid bit 1)? If not, stop and go to main memory (this is a miss).
- Does the entry’s tag equal t? If not, stop and go to main memory (this is also a miss).
- The line is valid and the tag matches, so this is a hit. We can use the data from this cache entry and avoid going to main memory.
Filling the Cache
On a cache miss, we need to fetch the value from main memory. (Let’s only consider loads for now; we’ll handle stores later.) Because this is slow, we want to avoid doing this again in the future. So, we want to do something called filling the cache entry. After fetching the data from main memory, do these things:
- Look in entry i of the cache (again).
- Is the entry valid? If so, there is already some data here, and we will take its place. This is called an eviction. (We will discuss more about what to do about evictions in the next section.)
- Set the valid bit to 1 (regardless of what it was before), to indicate that it contains real data now.
- Set the tag to t, to disambiguate which data it holds.
- Set the data to the value we got from main memory.
This way, subsequent accesses to the same address will hit. This is the way that caches exploit temporal locality, i.e., nearby-in-time accesses to the same address.
Example
To keep this example tractable, let’s pretend we only have 4-bit addresses (not 64). We’ll stick with a 4-entry cache, so the least-significant 2 bits are the index.
What happens when you execute this sequence of loads? Assume you start with en empty cache, where every entry is invalid. Label each access as a hit or a miss. Also, note each time an eviction occurs.
- load 1100
- load 1101
- load 0100
- load 1100
It can be helpful to draw out the four-column table above and update it after every access.
Larger Blocks
Our little cache is already pretty good at exploiting temporal locality, but we haven’t yet done anything about spatial locality. In our example above, when we access address 1100 and then immediately access 1101, both are misses even though the memory locations are “neighbors.” Under the hypothesis that many accesses in real applications will have spatial locality, we can extend the cache design to hit more often.
Here’s the idea. So far, every entry in our cache has only held a single memory address (and therefore only a single byte of data). Let’s generalize it to hold an entire block (a.k.a. line) of data, i.e., 2b bytes.
Before, we split the address into two pieces: the tag and the n-bit index. We will now split it into three. Listing from most-significant position to least-significant: the tag, the n-bit index, and the b-bit offset within the block.
You can visualize all of memory being broken up into 2b-byte blocks. The block is the unit of data that we will transfer to and from the cache. For example, when we fill data from main memory into the cache, we will fetch the entire 2b-byte block that contains a and put it into the cache. Now, loading a single byte brings in a bunch of neighbors—on the assumption that it’s likely that the program will soon need to access those neighbors.
The algorithm for accessing the cache remains the same; we just have to change the way we chunk up the address. And when we return data from the cache, we will use the least-significant b bytes as an offset to decide which byte from the block to return.
Example
Let’s return to our 4-byte cache from above. Let’s keep the design using 4 entries, but let’s make every entry store a 2-byte block instead of a single byte. That means our little 4-bit addresses now consist of 1 tag bit, 2 index bits, and 1 offset bit.
If you visualize this cache as a table, it looks exactly the same:
| index | valid? | tag | data |
|---|---|---|---|
| 00 | |||
| 01 | |||
| 10 | |||
| 11 |
The big difference now is that the “data” column stores 2-byte blocks. (The tag column now only stores 1 bit.)
Try simulating the same sequences of accesses again. Label the hits and misses:
- load 1100
- load 1101
- load 0100
- load 1100
Keeping Comparisons Fair
In this example, we cheated a bit: by doubling the size of the blocks, we double the total size of the cache. This means the cache is twice as big and twice as expensive. To make a fair comparison, between two cache designs, you’ll want to keep the total number of bytes the same. So if you double the block size, you should halve the number of entries.
Handling Stores
So far, we have only talked about loads (reads from memory). What about stores?
Writing to a cache works mostly the same as reading, except that we have a few choices to make.
- When we store to a block that is not already in the cache (a store miss), should we fill it (bring the block into the cache)? Or just send the write to memory? If so, this is called a write-allocate policy. Write-allocate caches make the (very reasonable) hypothesis that programs that write a given memory location are likely to read it again in the near future.
- When we store, should we just update the data in the cache, or should we also immediately send it to memory? The “immediately send all stores to main memory” policy is called write-through and it’s pretty simple. The other policy, where we just update the cache, is called write-back and it’s slightly more complicated.
The rest of this section will be about write-back caches. The write-back policy is a good idea in general because it means that you can avoid a lot of costly stores to main memory. It’s extremely popular for this reason. But it requires extra bookkeeping to deal with the fact that main memory and the cache can get “out of sync.”
Here’s the idea for keeping the cache and main memory in sync. We will add yet another value to our cache entries (another column in our table): the dirty bit. A cache entry is clean when it is in sync with main memory and dirty when it might disagree with main memory. Here’s how you can visualize the write-back cache:
| index | valid? | dirty? | tag | data |
|---|---|---|---|---|
| 00 | ||||
| 01 | ||||
| 10 | ||||
| 11 |
We will need to add these details to our algorithm for accessing the cache:
- When you fill a cache entry, initially set its dirty bit to 0. (The entry currently agrees with main memory.)
- Whenever you store to an entry in the cache, set its dirty bit to 1. (We are avoiding writing to main memory, so now a disagreement is possible.)
- Whenever you evict an entry from the cache, check its dirty bit. If the entry is clean, do nothing. If it’s dirty, write the data back to main memory then.
Example
Let’s try out a write-back policy with this sequence of accesses. Use our cache setup with 2-byte blocks as above.
- load 1100
- store 1101
- load 0100
- load 1100
Fully Associative Cache
All the caches we’ve seen so far have been direct-mapped: every block in main memory has exactly one cache entry where it might live. You may have noticed that these caches have a lot of evictions. Even when there is theoretically plenty of space in the cache, the fact that every block has only one option for where to live means that conflicts on these entries seem to happen all the time.
The opposite style of cache is a fully associative cache, where any memory address could use any entry in the cache. The index is no longer relevant at all; every cache entry could hold any address. When we divide up the address, you no longer take n bits for the index; the entire 64−b bits are one gigantic tag.
We will also change the cache-access algorithm. Where the direct-mapped algorithm says “look at entry i,” the fully associative version must look at every single entry in the cache, because the block we’re interested in might be anywhere.
Example
Let’s return to our 4-entry cache (with 2-byte blocks). In a fully associative version, because the indices are irrelevant, we can visualize it this way:
| valid? | tag | data |
|---|---|---|
There are 4 entries, all created equal, and they all might hold any address in all of memory. Let’s try the same sequence of loads again. Labels the hits and misses:
- load 1100
- load 1101
- load 0100
- load 1100
Replacement Policies
When you fill a block in a direct-mapped cache, there is only one choice of which existing block you should evict: the one that is in the (unique) entry where the block must live. In a fully associative cache, when the cache is full, you are now faced with a choice: which of the entries in the entire cache should we evict? An engineer designing a cache must decide on a replacement policy to answer this question.
There is an entire world of science dedicated to inventing cool eviction policies. The goal is to guess which block is least likely to be used again in the near future. And critically, it must make this decision efficiently—you can’t spend a lot of time thinking about which block to evict.
Some popular options include:
- Least-recently used (LRU): Keep track of the last time to access every block, and evict the one that was last used longest ago. The hypothesis is that, the longer a program goes not accessing a given block, the less likely it is to access it again soon. Unfortunately, LRU has a lot of overhead because you have to keep track of some kind of timestamp on every single block.
- Not most-recently used (NMRU): Like LRU, but only keep track of the most recently accessed block. When it comes time to evict, randomly pick some block that is not the most recent one you accessed. This makes somewhat worse decisions than LRU, but it’s a lot cheaper to implement and is popular for this reason.
The Costs of Associativity
Associativity is great! It leads to far fewer evictions. The problem is that it’s costly to implement in hardware. Because any block could go in any entry, we have to check all entries on every access to the cache. The hardware structure for implementing this “search all entries” operation is called a content-addressable memory (CAM). Because of the “search everywhere” nature of this operation, CAMs are expensive: large, hot, and slow. The cost scales with the number of entries, so it is only really practical to build fully associative caches when they are very small.
Set-Associative Cache
The final cache design we’ll consider strikes a balance between the direct-mapped and fully-associative extremes. A given address may live in exactly one entry in a direct-mapped cache; it may go in any entry in a fully associative cache; in a set-associative cache, it may live in one of a small number of entries grouped together into a set.
Let the number of entries in a set be 2k. In caching terminology, our cache has 2k ways. If there are 2n total entries in our cache, then there are 2n2k=2n−k sets. You can think of direct-mapped caches and fully associative caches as special cases:
- Direct-mapped: k=0, so there is only 1 way. There are 2n sets with a single block each.
- Fully associative: k=n, the it’s a 2n-way cache with only 1 (giant) set.
The usual way to visualize a set-associative cache is with a 2D grid of entries: one row per set, one column per way. Returning to our 4-entry cache with 2-byte blocks, we can make a visualization by copying and pasting two two-entry tables side by side:
| way 0 | way 1 | |||||
| index | valid? | tag | data | valid? | tag | data |
| 0 | ||||||
|---|---|---|---|---|---|---|
| 1 | ||||||
There are still 4 entries in this cache; they are now just grouped into sets of 2. This also means that the number of index bits goes from n to n−k (in this case, from 2 to 1) and the tags get correspondingly larger.
Let’s again update the algorithm for accessing the cache. After calculating the index, we now have to look at the entire set at that index. That means searching through all the ways (columns in our grid) associated with the index. And when we fill the cache after a miss, we need to choose which way within the set to evict using a replacement policy, just like in a fully associative cache.
Example
Once again, let’s simulate the same series of accesses on our machine with 4-bit addresses. This time, we will use a 4-entry, 2-way set associative cache, with a block size of 2. Use an LRU replacement policy. Here’s the sequence of loads again:
- load 1100
- load 1101
- load 0100
- load 1100
Understanding Cache Performance
With so many choices about how to design a cache, it can be useful to understand how well your cache is performing on average. You can characterize the overall performance by computing the average memory access time for the entire memory system. The average access time is:
tavg=thit+rmiss×tmiss
Where:
- thit is the time it takes to access the cache. Cache hits take exactly this amount of time; cache misses take this time to check the cache and then more time to go to main memory.
- tmiss is the time it takes to access main memory.
- rmiss is the miss rate: the fraction of accesses that are misses.
For example, if it take 1 ns to access the cache and 50 ns to access main memory, and 95% of accesses hit, then the average access time is 1+0.05×50=3.5 ns.
You can also extend this reasoning to multi-level cache hierarchies. Say you have an L1 cache and an L2 cache. From the perspective of the L1 cache, tmiss is the time it takes to access the rest of the cache hierarchy, i.e., to try accessing at L2. So you can calculate the average access time at the L2 cache and then use this average time as tmiss in the L1 access time calculation.
Three Categories of Misses
To understand the performance of some code (or of a cache design), you often want to pay attention to the cache misses. They can often be the slowest part of the program. It can also be useful to break down the misses by why they missed.
The 3 classic categories conveniently all start with the letter C:
- Cold or compulsory misses happen because this is the first access to the given cache line.
- Conflict misses happen because the associativity is too low, and too many lines competed for the same set and evicted a line that the program needed later on.
- Capacity misses happen because the entire cache is too small for the working set, and no amount of associativity could have helped.
Here’s an algorithm you can use to decide which category a miss belongs to:
- Was this cache line ever loaded before?
- If no: it’s a cold miss.
- If yes: Would this access have missed in a fully associative cache?
- If no: it’s a conflict miss.
- If yes: it’s a capacity miss.
OS Processes
So far in 3410, we have been operating under the ridiculous notion that a computer only runs one program at a time. A given program gets to own the computer’s entire memory, there is only a single program counter (PC) keeping track of a single stream of instructions to execute.
You know from your everyday computing life that this is not how “real” computers work. They can simultaneously run multiple programs with their own instructions, heap, and stack. The operating system (OS) is, among other responsibilities, the thing that makes it possible to run multiple programs on the same hardware at the same time. The next part of the course will focus on this mechanism: how the OS and hardware work together to work on multiple things concurrently.
Executable vs. Process
When you compile the C code you have written this semester, you produce an executable file. This is a file that contains the instructions and data for your program. An executable is inert: it’s not doing anything; it’s just sitting there on your disk. You can copy an executable, rename it, attach it to an email, print it out, put it on a floppy disk and send it through the US mail—anything you can do with any other file.
When you run an executable, that creates a process. A process is a currently running instance of a program. You can run the same executable multiple times and get multiple, concurrently executing processes of the same program. The different processes will share the same instructions and constant data, but they will have different heaps and different stacks (so different values of all their variables, potentially). It’s not just a file—you can’t print out a process or burn it to a CD. A process is something that occurs on a specific computer at a specific time.
Part of an operating system’s job is to provide processes with the illusion that they own the entire computer. That means that a process gets to use all of the machine’s registers without worrying about other processes using them at the same time. The OS manages the CPU’s program counter so it appears, to each process, to proceed normally through a given program’s instructions—without jumping willy-nilly to other programs’ instructions. Through a mechanism called virtual memory, every process gets the illusion of owning the entire 264-byte memory address space. (Virtual memory will be the topic of the next lecture.)
The Process Lifecycle
What happens when you type ./myprog in your shell to launch an executable?
(Assume you already compiled an executable, myprog.)
The OS must create a new process with the instructions and data from myprog.
The OS keeps track of the list of running processes.
Each process gets an entry in this list called a process control block (PCB).
The PCB includes metadata like the process id (pid),
information about the user who owns the process,
a current state of the process (running, waiting, ready, etc.),
and so on.
To create a new myprog process, the OS allocates a new PCB and adds it to its list of running processes.
Next, the OS sets up the memory for the process. Recall that programs expect to have access to regions of memory for their stack, heap, global data, and instructions. So at the very least, the OS needs to take the instructions from the executable and put them into memory. We’ll cover more about how to set up the memory address space for a process when we talk about virtual memory.
Finally, it’s time to run the process. The OS can transfer control to the program’s first instruction by setting the program counter to that instruction’s address.
It can be helpful to think about a process’s state (as tracked by its PCB) as a state machine.
Process states include initializing, runnable, running, waiting, and finished.
While setting up the PCB and the process’s memory, the OS places a new process in the initializing state.
Eventually, when this is all set up, the process becomes runnable.
Then, when the OS decides to finally start a process, it sets the PCB’s state to running.
The OS uses the waiting state for processes that are waiting for the OS to complete some task on its behalf (such as I/O).
Finally, after main eventually returns, the process enters the finished state.
Context Switching
Many processes may be active at the same time, i.e., they may all have PCBs that are all runnable. Only one process can actually be running at a time. The OS dedicates the CPU one process for a short span of time, and then it pauses that process and lets another process run for some time. While the length of these time windows varies by OS and according to how busy the computer is, you can think of them happening every 1–5 ms if it helps contextualize the idea. The OS aims to give a “fair” amount of time to each process.
The act of changing from running one process to running another is called a context switch. Here’s what the OS needs to do to perform a context switch:
- Save the current process state. That means recording the current CPU registers (including the program counter) somewhere in memory.
- Update the current process’s PCB (to exit the running state).
- Select another process. (Picking which one to run is an interesting problem, and it’s the responsibility of the OS scheduler.)
- Update that PCB to indicate that the process is now in the running state.
- Restore that process’s state: read the previously-saved register values back from memory.
- Resume execution by jumping to the new process’s current instruction.
Context switches are not cheap. Again as a very rough estimate, you can imagine them taking about a microsecond, or something like a thousand clock cycles. The OS tries to minimize the total number of context switches while still achieving a “fair” division of time between processes.
Kernel Space & User Space
The kernel is a special piece of software that forms the central part of the operating system. You can think of it as being sort of like a process, except that it is the first one to run when the computer boots and it has the special privilege of managing all the actual processes. The kernel has its own instructions, stack, and heap.
Systems hackers will often refer to a separation between kernel space and user space.
OS stuff happens in kernel space: maintaining the PCBs, choosing which processes to run, and so on.
All the stuff that the processes do (every single line of code in myprog above, for instance) happen in user space.
This is a cute way to refer to the separation of code and responsibilities between the two kinds of code.
However, there is also an important difference in privileges:
kernel-space code has unrestricted access to all of the computer’s memory and to I/O peripherals.
It can read and write the memory of any process.
User-space code, because of kernel-space machinations, gets that aforementioned illusion of running in a sandbox where it does not have to worry about other processes.
In user space, each process receives a limited number of privileges from the kernel and must ask the kernel nicely to perform things like I/O or to communicate with other processes.
Processor ISAs provide mechanisms to enforce this distinction in privileges. For example, RISC-V has a special set of privileged instructions and registers that only kernel-space code is allowed to use. The CPU starts in a state where these instructions are allowed; when the OS starts a user-space process, it instructs the CPU to take away access to these instructions. When control eventually transfers back into kernel space, the CPU re-enables access to these privileged instructions.
System Calls
On their own, the only things that processes can do are run computational instructions and access memory. They do not have a direct way to manage other processes, print text to the screen, read input from the keyboard, or access files on the file system. These are privileged operations that can only happen in kernel space. This privilege restriction is important because it puts the kernel in charge of deciding when these actions should be allowed. For example, the OS can enforce access control on files so an untrusted user can’t read every other user’s passwords.
Processes can ask the OS to perform privileged actions on their behalf using system calls. We’ll cover the ISA-level mechanisms for how system calls work soon. For now, however, you can think of a system call as a special C function that calls into kernel space instead of user space. (Calling a “normal” function always invokes code within the process, i.e., either code you wrote yourself or code you imported from a library.)
Each OS defines a set of system calls that it offers to user space. This set of system calls constitutes the abstraction layer between the kernel and user code. (For this reason, OSes typically try to keep this set reasonably small: a simpler OS abstraction is more feasible to implement and to keep secure.)
In this class, we’re using a standardized OS abstraction called POSIX. Many operating systems, including Linux and macOS, implement the POSIX set of system calls. (We’ll colloquially refer to it as “Unix,” but POSIX is the actual name of the standard.)
For a list of all the things your POSIX OS can do for you, see the contents of the unistd.h header.
That’s a collection of C functions that wrap the actual underlying system calls.
For example, consider the write function.
write is a low-level primitive for writing strings to files.
You have probably never called write directly, but you have used printf and fputc, both of which eventually must use the write system call to produce their final output.
Process Management
There are system calls that let processes create and manage other processes. These the big ones we’ll cover here:
exitterminates the current process.forkclones the current process. So after youfork, there are two nearly identical processes (e.g., with nearly identical heaps and stacks) running that can then diverge and start doing two different things.execreplaces the current process with a new executable. So after youexeca new program, you “morph” into an instance of that program.execdoes not create or destroy processes—the kernel’s list of PCBs does not grow or shrink. Instead, the current process transforms in place to run a different program.waitpidjust waits until some other process terminates.
fork
The trickiest in the bunch is probably fork.
When a process calls fork(), it creates a new child process that looks almost identical to the current one:
it has the same register values,
the same program counter (i.e., the same currently-executing line of code),
and the same memory contents (heap and stack).
A reasonable question you might ask is:
do the two processes (parent and child) therefore inevitably continue doing exactly the same thing as each other?
What good is fork() if it can only create redundant copies of processes?
Fortunately, fork() provides a way for the new processes to detect which universe they are living in:
i.e., to check whether they are the parent or the child.
Check out the manual page for fork.
The return value is a pid_t, i.e., a process ID (an integer).
According to the manual:
On success, the PID of the child process is returned in the parent, and 0 is returned in the child.
This is why I kept saying the two copies are almost identical—the difference is here.
The child gets 0 returned from the fork() call,
and the parent gets a nonzero pid instead.
This means that all reasonable uses of fork() look essentially like this:
#include <stdio.h>
#include <unistd.h>
int main() {
pid_t pid = fork();
if (pid == 0) { // Child.
printf("Hello from the child process!\n");
} else if (pid > 0) { // Parent.
printf("Hello from the parent process!\n");
} else {
perror("fork");
}
return 0;
}
In other words, after your program calls fork(), it should immediately check which universe it is living in:
are we now in the child process or the parent process?
Otherwise, the processes have the same variable values, memory contents, and everything else—so they’ll behave exactly the same way, aside from this check.
Another way of putting this strange property of fork() is this:
most functions return once.
fork returns twice!
exec
The exec function call “morphs” the current process, which is currently executing program A, so that it instead starts executing program B.
You can think of it swapping out the contents of memory to contain the instructions and data from executable file B and then jumping to the first instruction in B’s main.
There are many variations on the exec function; check out the manual page to see them all.
Let’s look at a fairly simple one, execl.
Here’s the function signature, copied from the manual:
int execl(const char *path, const char *arg, ...);
You need to provide the executable you want to run (a path on the filesystem) and a list of command-line arguments (which will be passed as argc in the target program’s main).
Let’s run a program! Try something like this:
#include <stdio.h>
#include <unistd.h>
int main() {
if (execl("/bin/ls", "ls", "-l", NULL) == -1) {
perror("error in exec call");
}
return 0;
}
That transforms the current process into an execution of ls -l.
There’s one tricky thing in the argument list:
by convention, the first argument is always the name of the executable.
(This is also true when you look at argc[0] in your own main function.)
So the first argument to the execl call here is the path to the ls executable file, and the second argument to execl is the first argument to pass to the executable, which is the name ls.
We also terminate the variadic argument list with NULL.
fork + exec = spawn a new command
The fork and exec functions seem kind of weird by themselves.
Who wants an identical copy of a process, or to completely erase and overwrite the current execution with a new program?
In practice, fork and exec are almost always used together.
If you pair them up, you can do something much more useful:
spawn a new child process that runs a new command.
You first fork the parent process, and then you exec in the child (and only the child) to transform that process to execute a new program.
The recipe looks like this:
fork()- Check if you’re the child. If so,
execthe new program. - Otherwise, you’re the parent. Wait for the child to exit (see below).
Here that is in code:
#include <stdio.h>
#include <unistd.h>
#include <sys/wait.h>
int main() {
pid_t pid = fork();
if (pid == 0) { // Child.
if (execl("/bin/ls", "ls", "-l", NULL) == -1) {
perror("error in exec call");
}
} else if (pid > 0) { // Parent.
printf("Hello from the parent!");
waitpid(pid, NULL, 0);
} else {
perror("error in fork call");
}
return 0;
}
This code spawns a new execution of ls -l in a child process.
This is a useful pattern for programs that want to delegate some work to some other command.
(Don’t worry about the waitpid call; we’ll cover that next.)
waitpid
Finally, when you write code that creates new processes, you will also want to wait for them to finish.
The waitpid function does this.
You supply it with a pid of the process you want to wait for (and, optionally, an out-parameter for some status information about it and some options),
and the call blocks until the process somehow finishes.
It’s usually important to waitpid all the child processes you fork.
Try deleting the waitpid call from the example above, and then compile and run it.
What happens?
Can you explain what went wrong when you didn’t wait for the child process to finish?
Signals
Whereas system calls provide a way for processes to communicate with the kernel, signals are the mechanism for the kernel to communicate with processes.
The basic idea is that there are a small list of signal values, each with its own meaning: a thing that the kernel (or another process) wants to tell your process. Each process can register a function to run when it receives a given signal. Then, when the kernel sends a signal to that process, the process interrupts the normal flow of execution and runs the registered function. Some signals also instruct the kernel to take specific actions, such as terminating the program.
There are also system calls that let processes send signals to other processes. (In reality, that means that process A asks the kernel to send the signal to process B.) This way, signals act as an inter-process communication/coordination mechanism.
Here are the functions you need to send signals:
kill(pid, sig): Sendsigto processpid.raise(sig): Sendsigto myself.
To receive signals, you set up a signal handler function with the signal function.
The arguments are the signal you want to handle and a function pointer to the code that will handle the signal.
Here’s an example of a program that handles the SIGINT signal:
#include <stdio.h>
#include <stdlib.h>
#include <signal.h>
#include <unistd.h>
void handle_signal(int sig) {
printf("Caught signal %d\n", sig);
exit(1);
}
int main() {
signal(SIGINT, handle_signal); // Set up the signal handler for SIGINT.
while (1) {
printf("Running. Press Ctrl+C to stop.\n");
sleep(1);
}
return 0;
}
The important bit is this line:
signal(SIGINT, handle_signal);
This line asks the kernel to register a function we’ve written so that it will run in response to the SIGINT signal.
Interrupts
We have already discussed signals: the mechanism that the kernel uses to communicate with user-space processes. Recall that, when your process receives a signal, it interrupts the normal flow of execution and runs the signal-handler function that you previously registered. How does this actually work? How does the kernel interfere with the execution of a process in between instructions, take control, and forcibly move the program counter to some other code?
Signals use a more general (and extremely important) mechanism called interrupts. As the name implies, they are the mechanism that the kernel uses to interrupt the execution of a running process, which is otherwise minding its own business and running one instruction after another, and make it do something else.
Here’s a conceptual way to think about how interrupts work. You can think of a CPU as executing a loop: fetch an instruction, execute that instruction, and then go back to the top of the loop. To deal with interrupts, CPU add an extra step to this conceptual loop: fetch an instruction, execute that instruction, check to see if there are any interrupts to handle, and then go back to the top of the loop. That is, you can imagine that there is some place where the CPU can look to see if there is an interrupt to deal with, and it checks for this indicator between the execution of adjacent instructions. When there is an interrupt to handle, the CPU transfers control to some code that can handle the interrupt.
What Are Interrupts For?
The OS and hardware uses interrupts to deal with exception conditions (what happens if your program runs out of memory? or executes an illegal instruction that the CPU cannot interpret?) and to support kernel-mediated services like I/O. Here are a few reasons why interrupts are helpful:
- They are more efficient than busy-waiting, i.e., just looping until something happens. If you’re waiting for a packet to arrive from the network, for example, you can execute other work until the packet arrives—at which point the OS can interrupt you to deliver the packet.
- They make it possible to handle events in the real world immediately. When the mouse moves, for example, the OS and hardware can interrupt the currently executing process to make sure the cursor appears to move on screen (instead of waiting patiently for the currently-running program to be done, which would make for a terribly janky mouse cursor).
- Interrupts are critical for multitasking, i.e., running multiple processes at once. Interrupts are what OS kernels use to perform periodic context switches between concurrent processes to fairly share CPU time between them.
As a result, systems use interrupts for a very wide variety of reasons, some of which are “exceptional” (e.g., when a program tries to execute an illegal instruction or references an unmapped virtual memory address) and others that are totally normal (e.g., to handle I/O or when it’s time to do a context switch).
Requesting Interrupts with System Calls
We also previously discussed system calls: the mechanism that user-space code uses to invoke kernel-space functionality. The underlying mechanism for system calls also uses interrupts. The ISA typically provides a special instruction that processes can use to request an interrupt. When the hardware executes this instruction, it immediately transitions to kernel mode to handle the system call.
To decide which system call to make and to pass arguments to it,
OSes define a syscall-specific calling convention.
This is different from the ordinary calling convention that governs the calling of ordinary functions.
If you’re curious, Linux’s manual page for the syscall C function lists its calling conventions for every architecture that Linux supports.
In RISC-V, the special instruction for making system calls is named ecall.
It has no operands.
The Linux syscall convention for RISC-V says:
a7contains the system call number. This decides which kernel functionality we want to invoke. For example, the syscall number forwriteis 64, and the number forexecveis 221.- Arguments to the system call go in
a0througha5. - The return value goes in
a0, just like in the “ordinary function” calling convention.
You can see a full list of available system calls on the syscalls(2) manual page.
Then, to find the corresponding syscall number, the authoritative source is the unistd.h header file in the Linux source code:
search for #define __NR_<call> <number>.
You can also try
this big, searchable syscall table that covers all the architectures Linux supports (use the “riscv64” column).
The corresponding manual page tells you the arguments for the syscall, expressed as a C function signature.
An Example
Let’s handcraft a system call in RISC-V assembly using ecall.
We will use the Linux write system call to output characters to the console.
If we look in unistd.h, it tells us that the syscall number for write is 64.
The manual page says that this system call takes 3 arguments:
ssize_t write(int fd, const void buf[.count], size_t count);
There is the file descriptor, a pointer to the characters to output, and the number of characters. The file descriptor 0 is the standard output stream, i.e., it’s how we print to the console. Let’s write a function that always outputs to file descriptor 0 and always prints exactly 1 character. Here are the assembly instructions we need:
addi a7, x0, 64 # syscall number: write
addi a0, x0, 0 # first argument: fd
mv a1, t0 # second argument: buf
addi a2, x0, 1 # third argument: count
ecall
We set the syscall number register, a7, to 64.
Then we provide the three arguments: file descriptor 0, a pointer (here I’m assuming it comes from t0), and length 1.
Finally, we use ecall to actually invoke the syscall.
Here’s a complete assembly file that wraps these instruction in a function for printing one-character strings:
.global printone
printone:
mv t0, a0 # save the function argument: a character pointer
# Make a system call: write(0, t0, 1)
addi a7, x0, 64 # syscall number: write
addi a0, x0, 0 # first argument: fd
mv a1, t0 # second argument: buf
addi a2, x0, 1 # third argument: count
ecall
ret
You can use this assembly from C code by writing a function declaration for it, like this:
int printone(char* c);
int main() {
printone("h");
printone("i");
printone("\n");
return 0;
}
You can compile and run the whole program by combining the C file and the assembly file:
$ rv gcc -o printone printone.c printone.s
This program prints something to the console without ever importing any headers or using the C standard library at all. Pretty cool!
Virtual Memory
We have previously said that part of the operating system’s job is give each process the illusion that it is running alone on the hardware. This concept is called virtualization: the OS runs on the physical hardware and provides an abstraction of virtual hardware for each process to run on. The OS virtualizes a single CPU by scheduling multiple concurrent processes to interleave their execution and orchestrating context switches between them.
This lecture is about how to virtualize the memory: i.e., how the OS creates the illusion, for every process, that the process has exclusive access to its own memory. The goal of a virtual memory system is that every process should have its own memory address space. In other words, we want the address 0xCAFED00D in process A to refer to different data from 0xCAFED00D in process B. (Maybe you can think about how bad life would be without virtual memory. Every process would need to carefully avoid using any addresses in use by any other process. And any process could freely access the memory of any other process. Shockingly, this is how many popular OSes worked until as late as the ’90s, and it was as terrible as it sounds.)
Virtual vs. Physical Memory Addresses
Here’s the overall strategy. We will make a distinction between the virtual address space for each process and the physical address space for the actual machine:
- Each process will operate in its own address space, meaning that it thinks in terms of its own 264 memory locations. We will call these addresses virtual addresses.
- The actual main memory has some number of bytes available—probably much fewer than 264. We will call the addresses of these “real” storage locations physical addresses.
The OS and hardware will collaborate to construct a mapping between virtual and addresses and physical addresses.
That is, for every process, we will create a table that describes, for every virtual address, the physical address where that data can be found.
The hardware has a special structure, called the memory management unit (MMU), that can translate from virtual to physical addresses.
Whenever a process tries to load or store an address V (e.g., it uses an lw or sb instruction with memory address V),
the hardware will automatically perform a virtual-to-physical memory address translation to find the corresponding physical address P.
It will then load or store the “real” memory location P.
This scheme means that programs never see physical addresses. They only know about virtual addresses, and all their instructions load and store those addresses. The hardware transparently translates all of these loads and stores into physical addresses to find the actual data. This way, processes can remain blissfully unaware of where their data is actually stored in the hardware and just think in terms of their own, private address space.
The data structure that describes the virtual-to-physical address translation is called the page table (for reasons we will see in a moment). The OS is responsible for setting up the page table and putting it into (physical) memory so the hardware knows where it is. When user-space code is running, the hardware then uses the page table to perform address translation. This is how the OS and hardware collaborate to implement virtual memory.
Pages and Page Tables
Let’s take a closer look at how page tables and address translation work.
An extremely inefficient way to set up a page table would be to explicitly record, for every virtual address in use, the corresponding physical address. This would mean that every single byte in a process’s virtual address space has its own, special mapping onto a specific byte in physical memory. This strawperson scheme is too fine grained: for one thing, it would require 8 bytes of address-mapping metadata for every byte of data!
Instead, VM systems divide all of memory up into chunks called pages. To give you a rough idea of the granularity, an extremely popular page size is 4 kB (4,096 bytes). You can imagine all of a process’s virtual address space, and all of the physical address space, divided up into these equally-sized chunks. Page tables work by mapping entire virtual pages (4 kB ranges of virtual addresses) onto physical pages (4 kB ranges of physical addresses).
As with cache blocks, this mapping works by dividing up the memory address. 4,096 is (2^{12}), so we will divide all memory addresses into the most-significant 52 bits and the least-significant 12 bits. The least-significant 12 bits are the offset within the page. The remaining (most-significant) 52 bits are the page number.
Some terminology: we will use virtual page number (VPN) and physical page number (PPN) when we’re talking about those non-offset bits in the address, depending on whether we’re referring to virtual or physical memory.
The page table then maps VPNs to PPNs. To translate a virtual address to a physical address, do these steps: split it into the page number (VPN) and the offset, translate the page number (from VPN to PPN), and then add the offset back on. Now you have a physical address.
The Memory Management Unit
The memory management unit (MMU) is the hardware structure that is responsible for translating virtual addresses to physical addresses. It uses a page table to perform this translation. But each process has its own page table—so how does the MMU know where to find the right page table at any given time?
The OS stores each process’s page table in main memory. (The kernel has the special privilege of using physical addresses directly, so it does not need to worry about address translation for its own accesses!) Then, when it performs a context switch, the OS needs to tell the hardware which page table is currently active for the process it is about to switch to. There is a special register that stores the (physical) address of the currently-active page table. The OS sets this register during each context switch to point to the relevant page table. Then, the MMU uses this register whenever it needs to perform address translations.
In RISC-V, this register is called satp.
You can read more about it in the privileged instruction manual.
Fancier Page Tables
You now know the basic mechanism for virtual memory: how the OS creates the illusion that every process is running in isolation. The rest of this lecture is about various extensions that build on the basic VM mechanism to do other cool stuff that systems need to do.
To support all of these extensions, VM systems enrich the page table with more metadata. Remember that the main thing that a page table needs to do is to map VPNs to PPNs: i.e., a basic version is nothing more than an array of PPNs indexed by VPN. In real systems, the page table also includes other stuff, like this:
- A valid bit, indicating whether the virtual page is mapped at all. (Kind of like the valid bit in a cache.) It is an error to access an address within an unmapped page.
- Protection bits. The OS can decide whether each page can be read, written, and/or executed. Think of this as 3 extra bits, named R, W, and X. It is an error, for example, to try to store to an address within a page whose W bit is 0. The X bit is especially important for security: the OS can prevent processes from executing instructions within writable memory (sometimes called the W^X restriction) to make it harder to exploit bugs that would otherwise trick the program into running malicious instructions.
You may also be worried that this sounds like a lot of data. If there are really 252 virtual pages, do we really need 252 entries in our page table? In practice, systems will compress this data structure using a multi-level page table, which lets the system omit chunks of entries for large ranges of invalid addresses. The details of these compressed data structures is out of scope for CS 3410.
Swap & Page Faults
There is one cool thing that virtual memory system enables that goes beyond isolating processes. VM can also let you transparently “overflow” your memory. If you run a bunch of programs that, all together, use more memory than you actually have available in your machine, the OS can transparently move some of their data to the disk. This mechanism is called swap, i.e., it works by swapping chunks of processes’ memory out to disk. (This mechanism is also called paging, because it involves moving pages around. Pages that are in memory are paged in or swapped in and pages that are relegated to the disk are paged out or swapped out.)
Processes do not need to be aware that their data has been swapped out. They can continue to pretend that they have unlimited access to all their memory. The OS takes care of moving data between main memory and the disk. Remember, accesses to the disk are much, much slower than main memory—so the OS tries to intelligently place frequently-accessed data in memory. The goal ends up very much like CPU caches: it exploits temporal and spatial locality to maximize the number of accesses that go to main memory, not to disk.
The strategy for implementing swapping is to mark paged-out memory as invalid in the page table. Remember that, when the CPU tries to access any virtual address, it must first consult the page table to perform protection checks (and to do the address translation). When the program accesses an invalid virtual page, a page fault occurs. The CPU uses an interrupt to transfer control to the kernel to handle the page fault.
There are many reasons that a page fault could occur.
It could be that the address is just unallocated:
the process never malloc’d that address.
(If you have ever gotten a segmentation fault error when running your C program (who hasn’t?), that’s what this means.)
The OS looks at its internal data structures to decide what happened:
i.e., to check whether the invalid virtual page is actually stored somewhere on disk.
If so, it pages in that data and then lets the process continue.
To page in new data, the OS reads the page from disk and places it into physical memory. This can mean evicting a different virtual page of data; the OS needs a replacement policy, just like in an associative cache, to decide which page to evict.
Because disks are so much slower than memory, swapping a page in takes a long time—think tens of milliseconds, roughly, or tens of thousands of clock cycles. So frequent swapping can seriously harm a program’s performance. And it’s enough time that the OS scheduler will likely try to find other work to do while the disk request is outstanding.
At a high level, swap lets disk join the memory hierarchy at a level below main memory. DRAM is sort of a cache for the hard disk; the CPU cache acts the same way for the DRAM; registers are kinda like a cache for the cache. It’s caches all the way down.
Sharing
Here is another cool thing that virtual memory enables. The page table translates virtual addresses to physical addresses; there is nothing intrinsic that requires this mapping to be injective. That is, if virtual address A in process X maps to physical address P, then it’s totally possible for virtual address B in process Y to map to exactly the same physical address P!
This observation implies a scheme where different processes can share the same data, without actually duplicating the data in main memory. Say that N different processes happen to need the same B bytes of data. With virtual memory, we can do this by spending only B total bytes of physical memory! Without VM, each process would need its own copy, for a total of N×B bytes.
There are a few situations where this kind of sharing is extremely useful in practice:
- Libraries. Multiple processes often need the same library code; they can share a read-only memory region to save space that would otherwise be duplicated for the library’s code.
- Inter-process communication. Process A can communicate with process B by writing into a memory region that the two processes share.
Threads
The next several lectures will all be about doing multiple computations at once. The point is that real software needs to deal with concurrency (managing different events that might all happen at the same time) and parallelism (harnessing multiple processors to get work done faster than a single processor on its own). Compared to sequential code, concurrency and parallelism require fundamental changes to the way software works and how it interacts with hardware.
Here are some examples of software that needs concurrency or parallelism:
- A web server needs to handle concurrent requests from clients. It cannot control when requests arrive, so they may be concurrent.
- A web browser might want to issue concurrent requests to servers. This time, the software can control when requests happen—but for performance, it is a good idea to let requests overlap. For example, you can start a request to server A, start a request for server B, and only then wait for either request to finish. That’s concurrency.
- A machine learning application wants to harness multiple CPU cores to make its linear-algebra operations go faster: for example, by dividing a matrix across several cores and working on each partition in parallel.
Threads are an OS concept that a single process can use to exploit concurrency and parallelism.
What Is a Thread?
A thread is an execution state within a process. One process has one or more threads. Each thread has its own thread-specific state: the program counter, the contents of all the CPU registers, and the stack. However, all the threads within a process share a virtual address space, and they share a single heap.
One way to define a thread is to think of it as “like a process, but within a process.” That is, you already know that processes have separate code (so they can run separate programs), register states, separate program counters, and separate memory address spaces. Threads are like that, except that threads exist within a process, and all threads within a process share their virtual memory. All threads within a process are running the same program (they have same text segment)—they may just execute different parts of that program concurrently.
When a process has multiple threads, it has multiple stacks in memory. Recall the typical memory layout for a process. When there are multiple threads, everything remains the same (the heap, text, and data segments are all unchanged) except that there are multiple stacks coexisting side-by-side in the virtual address space.
The threads within a process share a single heap. That means that threads can easily communicate through the heap: one thread can allocate some memory and put some data there and then simply let another thread read that data. This shared memory mechanism is both incredibly convenient and ridiculously error prone. (We will get more experience with the problems it can cause later.)
The thread’s state includes the registers (including the program counter and the stack pointer). The OS scheduler takes care of switching not only between processes but also between the threads in a process. When the computer has multiple CPU cores (as all modern machines do), the OS may also choose to schedule concurrent threads onto separate cores when there are multiple threads with work to do.
Synchronization
When you program with threads, you use a shared-memory parallelism programming model. This means that multiple streams of instructions are running simultaneously, and they can both read and write the same region of memory.
Problems abound in shared-memory parallelism. This lecture is about recognizing and fixing those problems.
Atomicity
For example, imagine that you have two threads that both concurrently run this line of C code:
*x += 1;
If the value x points to starts out at 0 before these two threads run, it would be nice if we could be guaranteed that that *x contained 2 after both threads finish.
But, as you know, *x += 1 is not a single action that your machine takes all at once.
You need to break it down into at least three steps:
load the value, add 1 to it, and then store it back to memory.
What can happen as these three steps from the two threads interleave?
For example, consider what happens if this ordering events happens:
- thread 1 loads the value
xpoints to - thread 2 loads the same value
- thread 1 increments the value
- thread 2 increments it
- thread 1 stores the modified value back to address
x - thread 1 stores its modified value back to address
x
What would the value of *x be then?
If this is not the intended behavior—if the programmer intended both copies of *x += 1 to take places as a single unit, resulting in the final value 2—then this is a violation of atomicity.
That is, the programmer might intend for an action like *x += 1 to be atomic: to happen all at once, without the ability for any thread to observe or interfere with the intermediate states between the beginning and the end of the operation.
But in C (and in the equivalent assembly), this is not an atomic operation: it consists of several smaller observations, and other threads can interfere in the middle.
Mutual Exclusion
Synchronization is a technique to avoid the problems that arise from shared-memory parallelism, such as atomicity violations. There are many forms of synchronization, and this lecture will explore a few of them.
An extremely popular form of synchronization is mutual exclusion, or mutex for short, also known as locking. The idea is that we want to delimit parts of the code where only one thread can be running at a time. Imagine that C had a special construct for mutual exclusion; then we might write this:
mutex {
x += 1;
}
This would mean that only one thread would be allowed to be running inside those curly braces at a time. The region of code protected by mutual exclusion (the code inside the braces inside this imaginary construct) is called a critical section. So if thread 1 entered the critical section, and then thread 2 arrived at the top of the section, it would need to wait until thread 1 left the critical section before it could enter.
Can you convince yourself that this mutual exclusion would fix the atomicity problems from our example? If we enforce mutually exclusive execution of that critical section, is that enough? (It is.)
Sadly, C does not have a built-in mutex construct.
Instead, we need to use a library or build it ourselves.
A Failed Attempt
Here’s a naive way that you might try to implement mutual exclusion: use a lock variable to keep track of whether someone is currently occupying the critical section.
Something like this:
int lock = 0;
while (lock) {} // Wait for the lock to be free.
lock = 1; // Acquire the lock.
*x += 1; // Critical section here.
lock = 0; // Release the lock.
That should do it, right? What happens if two different threads run this code concurrently?
It doesn’t work.
Imagine that both threads first encounter the while statement, and they both bypass it before setting lock to 1.
So we have failed to enforce mutual exclusion.
It’s possible to fall down a deep rabbit hole of techniques for implementing mutual exclusion. A famous example is Peterson’s algorithm, which works by combining one flag variable per thread (instead of one shared flag variable).
However, these custom algorithms for mutual exclusion are neither necessary nor sufficient. They are not necessary because CPUs provide special instructions just for implementing synchronization mechanisms such as mutual exclusion. They are not sufficient because CPUs implement optimizations that typically mean that any synchronization mechanism implemented using ordinary loads and stores, instead of the special instructions, cannot work reliably.
This insufficiency is a deep topic of its own that is out of scope for CS 3410, but here’s a brief summary. Please skip this paragraph unless you are super duper curious about an entirely separate branch of computer science. In a multiprocessor system, it takes a while for each processor to publish its memory stores so that they can be read by other processors. (The architectural component to blame is a store buffer.) That means that each CPU can read its own writes immediately, but other processors see these updates only after a delay. This results in a memory consistency model that allows updates to appear “out of order” to remote processors. Processors have therefore developed special instructions that bypass these optimizations and, at the cost of performance, force certain memory accesses to happen in a sequentially consistent order. All correct synchronization implementations, therefore, must use these special instructions instead of ordinary load and store instructions.
Atomic Instructions
RISC-V provides two basic atomic instructions to support the implementation of synchronization operations such as mutual exclusion.
They are called lr, for load reserved, and sc, for store conditional.
These two instructions work together to provide the basic mechanisms required to implement any style of synchronization.
(In other ISAs, this pattern is called load-link/store-conditional.)
The instructions come in different accesses sizes; for example, lr.w and sc.w are the word-sized (32-bit) versions.
Here’s what the instructions do:
lr.w rd, (rs1): Load the 32-bit value at the address inrs1and put the value inrd. (So far, like a normallw.) Also, create a “reservation” of this address. (What is a “reservation”? Keep reading.)sc.w rd, rs2, (rs1): Store the value ofrs2at the address inrs1. (Again, so far, like a normal store.) But, also check whether a reservation of this address exists. If so, then the store proceeds as normal, and setrdto 0. (Call this a “success.”) If not, then cancel the store altogether: do not write anything at all the memory, and setrdto 1. (This is a “failure.”)
This “reservation” business is a mechanism for checking whether anyone else wrote to a given address.
While a reservation exists, think of the CPU carefully monitoring the given address to see if anyone else writes to that address.
If nobody writes to the address between the lr and the sc, the reservation is preserved and sc succeeds.
If somebody else does write to the given address, then the reservation is lost and sc fails.
Implementing Synchronization Operations
The usual way to use lr and sc together is to put them at the beginning and the end of some region of code, and then wrap the whole thing in a loop.
The loop lets you try the code repeatedly, until the sc succeeds.
If you’re careful, this can mean that the code surrounded by the lr/sc pair eventually executes atomically.
The pattern looks something vaguely like this:
loop:
lr.w t0, (a0)
# ... do something with t0 to compute t1 ...
sc.w t2, t1, (a0)
bnez t2, loop # if the lr/sc failed, then try again
The memory address in this example is in register a0.
This little loop tries to do something with the value at this address and then store it back.
If any other thread ever interferes, then it gives up and tries again—over and over, until the operation succeeds.
The end result is that we get to perform an atomic operation on the value stored at the address in a0.
You will use this pattern to implement interesting synchronization operations, including mutual exclusion, in this week’s assignment.
Parallel Programming
One of the two motivations we used when introducing threads was the idea of harnessing parallel hardware to make computations go faster. Parallelism is important because the overwhelming majority of computers in the modern world are parallel. When was the last time (if ever) that you saw a laptop for sale with a single-core CPU? Core counts like 8 are much more common today. Even the Apple Watch has a dual-core processor. And on the other end of the spectrum, server processors have core counts like 96 and 192. The result is that, when performance matters, parallelism is the only way to take full advantage of the hardware.
Now that you know about the “building blocks” for parallelism (namely, atomic instructions), this lecture is about writing software that uses them to get work done. In CS 3410, we focus on the shared memory multiprocessing approach, a.k.a. threads. There are many other programming models for writing parallel software out there, but the shared-memory approach is ubiquitous: because they represent an incremental extension of a sequential programming paradigm, they are kind of the “default” way for modern software to incorporate parallelism.
pthreads
Last week’s assignment was on implementing synchronization operations to support parallel programming. It turns out that Unix has a standard library, called POSIX Threads or, affectionately, pthreads, that implements many of these sync ops for you. This lecture is about moving up the abstraction hierarchy: now that you know how these building blocks work, we can grant ourselves permission to use the “standard” version.
You can read the entire pthread.h header header to see what’s available.
Let’s walk through the basics step by step.
Spawn & Join Threads
The pthread_create function launches a new thread.
It’s a tiny bit like fork and exec for processes, but for threads within the current process instead of creating new subprocesses.
Here’s the signature:
int pthread_create(pthread_t* thread, pthread_attr_t* attr,
void *(*thread_func)(void*), void* arg);
We’ll come back to the other arguments, but the important ones for now are:
- The first argument,
thread, is apthread_tpointer to initialize. This struct is what the parent will use to interact with its brand-new child thread. - The third argument,
thread_func, is a function pointer to the code to run in the new thread. The thread function has to have a specific signature:void* thread_func(void* arg). Thevoid*argument and return types are C’s way of letting the thread function receive and return “anything.”
It’s OK (for now) to pass NULL for the other parameters.
So the basic recipe for spawning a new thread looks like this:
void* thread_func(void* arg) {
// code to run in a new thread!
}
// ...
pthread_t thread;
pthread_create(&thread, NULL, thread_func, NULL);
Whenever you spawn a thread, you will also want to wait for it to finish, a.k.a. join the thread.
There is a pthreads call for that too, in [the pthread_join function][join]:
int pthread_join(pthread_t thread, void** out_value);
We will again ignore the second parameter for a moment (it can be NULL).
The first parameter is the pthread_t value that we previously initialized with pthread_create.
The call blocks until the given thread finishes.
Putting it all together, here’s a complete program that launches a thread and then properly waits for it to finish:
#include <stdio.h>
#include <pthread.h>
void* my_thread(void* arg) {
printf("Hello from a child thread!\n");
return NULL;
}
int main() {
printf("Hello from the main thread!\n");
pthread_t thread;
pthread_create(&thread, NULL, my_thread, NULL);
pthread_join(thread, NULL);
printf("Main thread is done!\n");
return 0;
}
There are no race conditions here; this program is properly synchronized and is guaranteed to print the three messages in order:
Hello from the main thread!
Hello from a child thread!
Main thread is done!
Arguments & Return Values
Thread functions take a void* argument and return a void* return value so that the parent can communicate with it.
You pass a pointer to the argument value to pthread_create, and pthreads will pass this along to the thread function’s argument.
Then, if you return a value from the thread function, the parent can receive that value through an “out-parameter” in pthread_join:
that is, the parent has to wait for the child to finish for the return value to become available.
Here’s an example of a thread that performs the incredibly heavy-duty work of multiplying an integer by 2:
#include <stdio.h>
#include <pthread.h>
void* doubler_thread(void* arg) {
int* num = (int*)arg;
*num = *num * 2;
return arg;
}
int main() {
int my_number = 21;
printf("Before, my_number = %d\n", my_number);
pthread_t thread;
pthread_create(&thread, NULL, doubler_thread, &my_number);
int* result;
pthread_join(thread, (void**)&result);
printf("Result returned: %d\n", *result);
printf("After, my_number = %d\n", my_number);
return 0;
}
The parent passes a pointer to my_number to the doubler_thread thread function.
The thread function then passes the same pointer right back to the parent.
While thread arguments are really important, to be honest, I don’t usually find thread return values all that useful. It’s usually easier to just use the thread argument: to pass a pointer to where the thread should write its results. You’ll see that happen in the rest of the examples in this lecture.
Launching Lots of Threads
You usually want to create many threads at once, not just one.
You still need one pthread_t per thread, so a good tactic is to use an array (on the stack or the heap) of these.
Use a loop to launch the threads with pthread_create,
and then another loop to wait for each one with pthread_join.
Here’s an example that launches one thread per number in a range to check if it’s prime (in the slowest way possible):
#include <stdio.h>
#include <pthread.h>
#include <stdbool.h>
#define NUMBERS 20
bool is_prime(int n) {
for (int i = 2; i < n; ++i) {
if (n % i == 0) {
return false;
}
}
return true;
}
typedef struct {
int number;
bool* prime_flags;
} my_thread_args_t;
void* prime_thread(void* args_in) {
my_thread_args_t* args = (my_thread_args_t*)args_in;
args->prime_flags[args->number] = is_prime(args->number);
return NULL;
}
int main() {
// We'll set `prime[i]` to true iff `i` is prime.
bool prime[NUMBERS];
// Launch a thread to check every number.
pthread_t threads[NUMBERS];
my_thread_args_t thread_args[NUMBERS];
for (int i = 1; i < NUMBERS; ++i) {
thread_args[i] = (my_thread_args_t){
.number = i,
.prime_flags = prime,
};
pthread_create(&threads[i], NULL, prime_thread, &thread_args[i]);
}
// Join all threads and print results when ready.
for (int i = 1; i < NUMBERS; ++i) {
pthread_join(threads[i], NULL);
printf("%d is %s\n", i, prime[i] ? "prime" : "composite");
}
return 0;
}
This example also demonstrates another useful technique: defining your own little struct just to use as the argument to the thread function.
If thread functions could take multiple arguments, we might just do that.
But using a struct for the arguments is the next best thing.
Here, my_thread_args_t contains the number that the thread is supposed to process and a pointer to the results array where it should write.
To ensure that the argument struct remains “alive” for the entire duration of the thread, we also need an array to store all these my_thread_args_t values.
(It would not work, for example, to use a local variable inside the loop.)
Make Threads Do Coarse-Grained Chunks of Work
Threads are not free. Launching a thread takes time to coordinate with the OS; joining similarly costs waiting time; each running thread costs bookkeeping memory; and frequent context switching between threads adds overhead. And if you are aiming to fully harness a parallel CPU, it doesn’t help to have more threads than you have available hardware parallelism anyway.
It is therefore not a good idea to launch threads that only do a tiny amount of work, such as checking a single number for primality. Checking thousands or millions of numbers is perfectly practical, but launching millions of threads to check each one is not. In practical programming, you will want to divide a problem into coarser-grained chunks of work. Then you can launch a small number of threads—probably somewhere close to the number of cores in your machine.
For our primality example, it could make sense to divide up the numbers we need to check.
We can extend our my_thread_args_t struct to contain not just one number but a start/end interval.
Then, we just need to change our thread to loop over the range.
Here’s a full implementation:
#include <stdio.h>
#include <pthread.h>
#include <stdbool.h>
#define THREADS 8
#define NUMBERS 1024
bool is_prime(int n) {
for (int i = 2; i < n; ++i) {
if (n % i == 0) {
return false;
}
}
return true;
}
typedef struct {
int start_number;
int end_number;
bool* prime_flags;
} my_thread_args_t;
void* prime_thread(void* args_in) {
my_thread_args_t* args = (my_thread_args_t*)args_in;
for (int n = args->start_number; n < args->end_number; ++n) {
args->prime_flags[n] = is_prime(n);
}
return NULL;
}
int main() {
// We'll set `prime[i]` to true iff `i` is prime.
bool prime[NUMBERS];
// Launch a thread to check chunks of numbers.
pthread_t threads[THREADS];
my_thread_args_t thread_args[THREADS];
int numbers_per_thread = NUMBERS / THREADS; // Hopefully they divide.
for (int i = 0; i < THREADS; ++i) {
thread_args[i] = (my_thread_args_t){
.start_number = i == 0 ? 1 : i * numbers_per_thread,
.end_number = (i + 1) * numbers_per_thread,
.prime_flags = prime,
};
pthread_create(&threads[i], NULL, prime_thread, &thread_args[i]);
}
// Join all threads and print results when ready.
for (int i = 0; i < THREADS; ++i) {
pthread_join(threads[i], NULL);
for (int n = thread_args[i].start_number;
n < thread_args[i].end_number;
++n) {
printf("%d is %s\n", n, prime[n] ? "prime" : "composite");
}
}
return 0;
}
The nice thing about this version is that the problem size (the number of integers to check for primality) is not related to the thread count. So we can freely change the two parameters independently.
Concurrency Bugs
Sadly, parallel programming comes with an entirely new category of bugs to worry about. You have already seen atomicity violations, for example, and many other forms of concurrency bugs also lurk in shared-memory programming. In essence, the whole game of parallel programming is avoiding concurrency bugs without sacrificing too much of the awesome performance potential of parallel hardware.
A Racy Program
Let’s try changing our multithreaded primality checker to, instead of reporting which numbers are prime, just count how many primes exist in a range of numbers. Here’s the complete program:
#include <stdio.h>
#include <pthread.h>
#include <stdbool.h>
#define THREADS 8
#define NUMBERS 1024
bool is_prime(int n) {
for (int i = 2; i < n; ++i) {
if (n % i == 0) {
return false;
}
}
return true;
}
typedef struct {
int start_number;
int end_number;
int* prime_count;
} my_thread_args_t;
void* prime_thread(void* args_in) {
my_thread_args_t* args = (my_thread_args_t*)args_in;
for (int n = args->start_number; n < args->end_number; ++n) {
if (is_prime(n)) {
(*(args->prime_count))++;
}
}
return NULL;
}
int main() {
int primes = 0;
// Launch a thread to check chunks of numbers.
pthread_t threads[THREADS];
my_thread_args_t thread_args[THREADS];
int numbers_per_thread = NUMBERS / THREADS; // Hopefully they divide.
for (int i = 0; i < THREADS; ++i) {
thread_args[i] = (my_thread_args_t){
.start_number = i == 0 ? 1 : i * numbers_per_thread,
.end_number = (i + 1) * numbers_per_thread,
.prime_count = &primes,
};
pthread_create(&threads[i], NULL, prime_thread, &thread_args[i]);
}
// Join all threads.
for (int i = 0; i < THREADS; ++i) {
pthread_join(threads[i], NULL);
}
// Print final prime count.
printf("%d numbers in the range 1-%d are prime\n",
primes, (NUMBERS - 1));
return 0;
}
When I compiled and ran this program on my machine, it gave disturbingly inconsistent answers. Here are a few runs:
$ gcc -O2 threads-racy.c -o racy
$ ./racy
153 numbers in the range 1-1023 are prime
$ ./racy
163 numbers in the range 1-1023 are prime
$ ./racy
154 numbers in the range 1-1023 are prime
$ ./racy
167 numbers in the range 1-1023 are prime
$ ./racy
153 numbers in the range 1-1023 are prime
$ ./racy
159 numbers in the range 1-1023 are prime
$ ./racy
161 numbers in the range 1-1023 are prime
It’s bad enough that these answers are incorrect, but even worse, the program is nondeterministically incorrect.
The problem is reminiscent of the basic atomicity violation that we saw recently, but it actually indicates an even deeper problem.
Data Races
The fundamental problem in the buggy program above is an unsynchronized memory access. The formal name is a data race. Here’s a definition: a data race occurs when two different threads perform unsynchronized accesses to the same memory location, and at least one of those accesses is a write.
To understand this definition, is an be useful to think through things that are not data races:
- Memory accesses within a single thread. Memory accesses can of course be buggy for other reasons, but they are not data races!
- When different threads access different memory locations. In our original primality check program, for example, different threads wrote to different
primes[i]indices. But no to threads ever tried to write to the same index, so there was no data race. - Multithreaded reads of the same data. It is always OK for different threads to share read-only data. The only situations that are data races are when one thread writes and the other thread reads and when both threads write.
The final criterion is that unsynchronized qualifier. This has a more nuanced definition, but it broadly means that there are no synchronization operations (such as locks) protecting the data. The implication is that you can always fix data races by adding synchronization.
The line in our program with the data race is this one:
(*(args->prime_count))++;
Let’s check the four parts of our definition:
- Multiple threads run this line.
- The access is unsynchronized: we haven’t done anything to ensure ordered access.
- The accesses go to the same memory location. (There is only one
prime_countvariable.) - Although the
++syntax makes it slightly harder to see, this line both reads and writes the variable.
So this is indeed a data race.
Data races are undefined behavior in C (and C++). That means that they are equally problematic as a violation of the heap commandments: use-after-free bugs, out-of-bounds accesses, and so on. The compiler is allowed to assume your program does not have races and transform and bases its optimizations on that assumption.
The consequence is that you cannot reason about the behavior of racy programs; they can do anything. To write working parallel software, you must avoid data races.
Locks in pthreads
You can fix data races by adding synchronization. We could even use the spin-lock mutex that is on your current assignment. But pthreads also provides a mutual exclusion lock. There are three steps to use a pthreads lock:
- Initialize it. You can use the
pthread_mutex_initfunction or thePTHREAD_MUTEX_INITIALIZERconstant. - Acquire the lock with the
pthread_mutex_lockfunction. - When your critical section is done, release the lock with the
pthread_mutex_unlockfunction.
To fix our racy program above, we can declare a new mutex in main:
pthread_mutex_t mutex = PTHREAD_MUTEX_INITIALIZER;
Then, we’ll need to pass this mutex along to each thread by adding it to our my_thread_args_t struct.
Within each thread, we’ll acquire and release the mutex to protect a critical section:
pthread_mutex_lock(args->mutex);
(*(args->prime_count))++;
pthread_mutex_unlock(args->mutex);
We now have a properly synchronized program with no data races. If we run this program, it reliably gets the right answer:
$ gcc -O2 threads-mutex.c -o mutex
$ ./mutex
173 numbers in the range 1-1023 are prime
$ ./mutex
173 numbers in the range 1-1023 are prime
$ ./mutex
173 numbers in the range 1-1023 are prime
Catching Races with Thread Sanitizer
To catch other forms of undefined behavior such as out-of-bounds accesses, we recommend enabling sanitizers in the compiler. Is there a similar way to detect data races?
Fortunately, yes:
ThreadSanitizer is a feature built into some compilers that does exactly this.
Unfortunately, it doesn’t (yet) work in the CS 3410 RISC-V container.
But if you like and you have a recent compiler set up on your host machine, you can enable ThreadSanitizer with -fsanitize=thread.
For example, this will find the data race in our buggy example above (before we added the lock):
$ clang -g -fsanitize=thread threads-racy.c -o racy
$ ./racy
==================
WARNING: ThreadSanitizer: data race (pid=56484)
Write of size 4 at 0x00016dd9efe0 by thread T2:
#0 prime_thread threads-racy.c:28 (racy:arm64+0x100003c04)
Previous write of size 4 at 0x00016dd9efe0 by thread T1:
#0 prime_thread threads-racy.c:28 (racy:arm64+0x100003c04)
[...]
This error indicates that line 28 of threads-racy.c had a data race with itself.
Producer/Consumer Parallelism
Locks and critical sections are only one way to coordinate work between multiple threads. This section will build up toward a different style.
One limitation in our approach so far to diving work into chunks is imbalance between threads. Our primality program, for example, takes as long as the slowest thread. Larger numbers take longer to check, so the earlier chunks will run faster than the later chunks. Dealing with this kind of imbalance is a major challenge in parallel programming.
One parallel programming technique to help automatically deal with imbalance is the producer/consumer pattern. The idea is that you will have one thread producing the work to do and n parallel threads consuming the work items and actually doing the work. You need a data structure keep track of the work and to intermediate between the producer and the consumers.
We’ll start by designing that data structure and then build up to a new automatically-balancing implementation of our primality checker.
Circular Buffer
We need a queue data structure to intermediate between the producer and the consumers. The idea is that the producer will push work items on to the tail of the queue, and consumers will pop items from the head.
A sensible way to implement a bounded-size queue is with a circular buffer (a.k.a. a ring buffer). The idea is to allocate an array of n elements, and to hope that you never need to have more than n things in your queue at once. Then, you keep track of two indices: the head and the tail of the queue. They “wrap around” the n-element array.
Here’s a sample implementation of a bounded buffer without any parallelism involved.
We’ll need a struct to keep track of the state:
typedef struct {
int* data;
int capacity; // The size of the `data` array.
int head; // The next index to pop.
int tail; // The next index to push.
} bounded_buffer_t;
Here are the functions to push into and pop from the queue:
void bb_push(bounded_buffer_t* bb, int value) {
assert(!bb_full(bb));
bb->data[bb->tail] = value;
bb->tail = (bb->tail + 1) % bb->capacity;
}
int bb_pop(bounded_buffer_t* bb) {
assert(!bb_empty(bb));
int value = bb->data[bb->head];
bb->head = (bb->head + 1) % bb->capacity;
return value;
}
The functions work by advancing the head or tail index by one and then “wrapping around” the capacity-sized array.
There is a critical detail here represented by the assert calls.
(You can imagine simple implementations of bb_full and bb_empty: the buffer is empty if the head and tail indices are equal, for example.)
We really don’t want to push into a full buffer or pop from an empty queue.
When we take this data structure into a parallel context, we will want to handle these conditions by waiting for some other thread to do push or pop before proceeding with our own operation.
A Simple Lock and Busy Waiting
One way to make the producer/consumer pattern work to wrap all our accesses to the queue in a lock, just like any other shared data structure.
We’ll start by extending the queue data structure:
typedef struct {
int* data;
int capacity; // The size of the `data` array.
int head; // The next index to pop.
int tail; // The next index to push.
pthread_mutex_t* mutex;
bool done;
} bounded_buffer_t;
We add a mutex to protect the lock, and also a done flag to signal to consumers that there are no more items coming.
Next, we will implement variants of the bb_push and bb_pop functions that are safe to call from separate threads, and which block (wait) until they can succeed.
Our goal is to write a couple of thread functions like this:
void* producer_thread(void* arg) {
bounded_buffer_t* buf = (bounded_buffer_t*)arg;
for (int i = 0; i < NUMBERS; ++i) {
printf("producing %d\n", i);
bb_block_push(buf, i);
}
bb_finish(buf);
return NULL;
}
void* consumer_thread(void* arg) {
bounded_buffer_t* buf = (bounded_buffer_t*)arg;
while (1) {
bool done;
int number = bb_block_pop(buf, &done);
if (done)
break;
printf("consuming %d\n", number);
}
return NULL;
}
The producer thread pushes the numbers 0 through NUMBERS-1 into the queue.
Whenever the queue is full, bb_block_push should wait until there is room and then proceed.
The consumer thread pops one number at a time.
The bb_block_pop call blocks until there is at least one item in the queue to consume or until the done flag becomes true, in which case the thread should shut down.
Let’s look at bb_block_push first:
void bb_block_push(bounded_buffer_t* bb, int value) {
pthread_mutex_lock(bb->mutex);
// Spin to wait until the queue has room to push.
while (bb_full(bb)) {
// Release the lock for a moment to let other threads proceed.
pthread_mutex_unlock(bb->mutex);
pthread_mutex_lock(bb->mutex);
}
// Actually do the push.
bb_push(bb, value);
pthread_mutex_unlock(bb->mutex);
}
This is a busy waiting loop: we repeatedly check for there to be room in the queue, and when there finally is, then we push. The tricky thing I’ve done here is to briefly unlock and relock the buffer’s mutex. If we didn’t do this, no other thread could acquire the lock to pop, so we could never make progress.
The critical sections here (regions between a pthread_mutex_lock and pthread_mutex_unlock) here are a little harder to see because of this trick.
But they protect all the shared state:
all the accesses to the buffer’s internal data happen with the lock held.
The bb_block_pop function looks somewhat similar:
int bb_block_pop(bounded_buffer_t* bb, bool* done) {
pthread_mutex_lock(bb->mutex);
// Spin to wait until queue has a value (or until we are done).
while (bb_empty(bb) && !bb->done) {
pthread_mutex_unlock(bb->mutex);
pthread_mutex_lock(bb->mutex);
}
// Either we're done or we can pop.
int value;
if (bb->done) {
*done = true;
value = 0;
} else {
value = bb_pop(bb);
}
pthread_mutex_unlock(bb->mutex);
return value;
}
One main difference here is that we also need to check for the done flag.
Because it’s shared state, that access also needs to be protected by the buffer’s mutex.
This implementation totally works. It is a little sad that we had to resort to busy-waiting, though: it is inefficient to need to repeatedly acquire a lock to check a condition until it happens to change. This should be a clue that a mutex alone may not be the perfect tool for the job.
Condition Variables
This is a perfect use case for a different synchronization construct: a condition variable. You always pair a condition variable with a lock. Condition variables let you temporarily release the lock while you wait for other threads to change some condition you care about. In this case, the condition we need to wait for is the fullness or emptiness of the buffer.
The pthreads library provides a pthread_cond_t type for condition variables.
Aside from initialization/destruction, there are three important operations:
pthread_cond_wait(cond, mutex): Call this function while you already holdmutex. The function temporarily releasesmutex, waits for a signal from another thread on the condition variablecond, and then re-acquiresmutex.pthread_cond_signal(cond): Signal (i.e., wake up) one thread that is currently waiting oncond.pthread_cond_broadcast(cond): Signal all threads that are waiting oncond.
An important thing to realize about the condition variable API is that it doesn’t say anything about whether an actual logical condition about your program is true or false. That’s up to you. It just handles the mechanics of waiting for the abstract idea of condition changes.
The Correct Way™ to use condition variables is to wait on them in a loop that checks your actual, logical condition to become true. Something like this:
pthread_mutex_lock(mutex);
while (!check_your_condition()) {
pthread_cond_wait(cond, mutex);
}
do_stuff(); // Now you know `check_your_condition()` returned true.
pthread_mutex_unlock(mutex);
The specification for pthread_cond_wait allows for spurious wakeups:
the call can sometimes return even when nobody signaled.
That’s why it’s a good idea to always put your wait call in a loop that checks whether the condition actually changes.
It also lets other threads “err on the side of signalling”:
it is OK to signal a condition even if there’s a chance the logical condition did not actually change.
Because you know all the waiting threads will double-check the condition in their loops, you can feel safe in signalling even when you don’t strictly need to.
Using Condition Variables in the Producer/Consumer Pattern
Let’s try replacing the busy waiting in our producer/consumer program with condition variables.
We will associate two pthread_cond_t condition variables with our buffer in its definition:
typedef struct {
int* data;
int capacity; // The size of the `data` array.
int head; // The next index to pop.
int tail; // The next index to push.
pthread_mutex_t* mutex;
bool done;
pthread_cond_t* full_cv;
pthread_cond_t* empty_cv;
} bounded_buffer_t;
The two condition variables reflect two abstract states:
whether the queue is full and whether it is empty.
We’ll signal the full_cv condition variable when the buffer goes from full to non-full.
Similarly, we’ll signal empty_cv when it goes from empty to non-empty.
Here’s what the push function looks like with condition variables:
void bb_block_push(bounded_buffer_t* bb, int value) {
pthread_mutex_lock(bb->mutex);
while (bb_full(bb)) {
pthread_cond_wait(bb->full_cv, bb->mutex);
}
bb_push(bb, value);
pthread_mutex_unlock(bb->mutex);
pthread_cond_signal(bb->empty_cv);
}
The loop looks pretty similar; we just get to replace that unlock/lock pair with a pthread_cond_wait.
The wait call appears in a loop that checks the actual logical condition.
After the critical section finishes, we know that the queue’s emptiness may have changed, so we signal the empty_cv condition.
We can change the pop function in a similar way:
int bb_block_pop(bounded_buffer_t* bb, bool* done) {
pthread_mutex_lock(bb->mutex);
while (bb_empty(bb) && !bb->done) {
pthread_cond_wait(bb->empty_cv, bb->mutex);
}
int value;
if (bb->done) {
*done = true;
value = 0;
} else {
value = bb_pop(bb);
}
pthread_mutex_unlock(bb->mutex);
pthread_cond_signal(bb->full_cv);
return value;
}
This time, we need to signal the full_cv condition because, after this pop is done, the queue may have just gone from full to non-full.
The code is shorter this way, and the pthreads library can help put these threads to sleep while they’re waiting. Awesome!
Deadlock
We have seen two types of concurrency bugs so far: atomicity violations and data races. This section is about a third kind. Deadlock is the name for the problem that happens when two different threads get stuck waiting for the other.
Here’s the general scenario. Imagine a situation with two threads, T1 and T2, that need to use some sort of shared resources, R1 and R1. The program wants to prevent concurrent use: i.e., only one thread can be using a resource at a given time. Now imagine that T1 is currently using only R1 and T2 is currently using only R2. Next, imagine that T1 also wants to start using R2, and that T2 wants to start using R1. Because R2 is busy, T1 must wait for T2 to be done with it. Similarly, because R1 is busy, T2 must wait. Neither thread can make progress, so neither can relinquish their reservation on either resource. So we are stuck.
An Example
We can turn this abstract idea into real code using locks. We’ll spawn two threads, and use two locks (representing the shared resources R1 and R2 above). The program looks like this:
#include <stdio.h>
#include <pthread.h>
pthread_mutex_t lock1 = PTHREAD_MUTEX_INITIALIZER;
pthread_mutex_t lock2 = PTHREAD_MUTEX_INITIALIZER;
void* thread1(void* arg) {
printf("Hello from a thread 1!\n");
pthread_mutex_lock(&lock1);
/*** Potential deadlock here! ***/
pthread_mutex_lock(&lock2);
pthread_mutex_unlock(&lock2);
pthread_mutex_unlock(&lock1);
return NULL;
}
void* thread2(void* arg) {
printf("Hello from a thread 2!\n");
pthread_mutex_lock(&lock2);
/*** Potential deadlock here! ***/
pthread_mutex_lock(&lock1);
pthread_mutex_unlock(&lock1);
pthread_mutex_unlock(&lock2);
return NULL;
}
int main() {
printf("Hello main!\n");
pthread_t threads[2];
pthread_create(&threads[0], NULL, thread1, NULL);
pthread_create(&threads[1], NULL, thread2, NULL);
pthread_join(threads[0], NULL);
pthread_join(threads[1], NULL);
printf("Main is done!\n");
return 0;
}
I’ve added a comment to mark the problematic point in both threads.
If both threads were to reach that point at the same time,
then thread1 would need to wait for thread2 to release lock2 and vice versa.
Deadlock!
If you try to compile and run this example, however, it will be hard to make this potential deadlock manifest. You have to get unlucky with the relative progress of the two threads. If one thread happens to finish before the other one even gets started, for example, there’s no deadlock here.
This is the worst kind of concurrency bug: the kind that manifests rarely. If the bug happens every time, that’s not great, but at least you can find it, reproduce it and fix it. If you have a bug manifest only once every N days or months, it’s hopeless: you can recreate exactly the same conditions that led to the bug and not be able to trigger the behavior so you can inspect it. As one recent example, here’s a blog post from some Netflix engineers about an intermittent concurrency bug (not a deadlock, but the point still stands). In that story, it was easier to just periodically kill the problematic processes than to find and fix the bug.
Just so we can prove it’s a problem, we can force the deadlock to happen every time by synchronizing the threads at the problematic point. Like this:
void* thread1(void* arg) {
printf("Hello from a thread 1!\n");
pthread_mutex_lock(&lock1);
barrier();
printf("Passed the barrier in thread 1!\n");
pthread_mutex_lock(&lock2);
pthread_mutex_unlock(&lock2);
pthread_mutex_unlock(&lock1);
return NULL;
}
void* thread2(void* arg) {
printf("Hello from a thread 2!\n");
pthread_mutex_lock(&lock2);
barrier();
printf("Passed the barrier in thread 2!\n");
pthread_mutex_lock(&lock1);
pthread_mutex_unlock(&lock1);
pthread_mutex_unlock(&lock2);
return NULL;
}
By using a barrier to make the threads reach the point just before they acquire the second lock, we can make the deadlock manifest deterministically.
A Rule for Avoiding Deadlock
The crucial mistake that makes our example above deadlock is that the threads acquire the locks in different orders.
thread1 has a lock1 critical section surrounding a lock2 critical section; thread2 acquires and releases the locks in the opposite order.
Think about what would happen instead if both threads acquired lock1 and then, within that critical section, had a smaller lock2 critical section.
It turns out that you can use this observation to concoct a rule for avoiding deadlocks when using mutexes:
- Decide on a total order among all your mutexes.
- Always acquire the mutexes in that order.
- Always release them in opposite order.
A different way of describing the third element in the rule is that, when critical sections overlap, one should always entirely contain the other—they should never partially overlap. So this is OK:
pthread_mutex_lock(&lock1);
// do stuff with one lock
pthread_mutex_lock(&lock2);
// do more stuff with both locks
pthread_mutex_unlock(&lock2);
// do even more stuff with just lock1
pthread_mutex_unlock(&lock1);
But this is not, because neither critical section entirely contains the other:
pthread_mutex_lock(&lock1);
// do stuff with one lock
pthread_mutex_lock(&lock2);
// do more stuff with both locks
pthread_mutex_unlock(&lock1);
// do even more stuff with just lock2
pthread_mutex_unlock(&lock2);
If you always “scope” your critical sections, and you always acquire your locks in a consistent order, you can avoid deadlock that arises from locks.
Performance in Parallel Programming
Performance Experiments
Let’s measure the performance of our producer/consumer primes counter. I’ve created a version that varies the number of worker threads from 1 to 16. For each worker-thread count, it runs the entire parallel system 10 times and takes the average wall-clock running time. If you want to play along at home, here’s the complete code.
This self-timing program prints things out in CSV format. When I ran this on my machine once, it printed these results:
workers,us
sequential,134134
1,142127
2,73236
3,52692
4,40498
5,36086
6,30115
7,26235
8,24882
9,25613
10,26563
11,27110
12,26788
13,25381
14,26397
15,26917
16,28449
The numbers here are microseconds. I’ve also included, on the first row, the time for a purely sequential version—one with a single thread, no mutexes, no bounded buffers, and no condition variables.
Let’s plot these times:
It looks like adding threads makes the program go faster, which is great. It also levels out at certain point, and maybe even starts to get a little worse. This also makes sense: once we have used up all the parallel hardware resources in my machine, adding more threads doesn’t help, and it can even hurt because the threads need to spend more time synchronizing. The machine I used for this experiment has 8 hardware thread contexts, which is why things don’t get any faster after that.
Speedup and Scalability
Another way to look at this data is to compute the speedup: the ratio you get when you divide the time taken to run on 1 thread by the time taken with n threads. A speedup of 2.0, for example, means that the program ran 2 times faster than the baseline.
We can plot those numbers too:
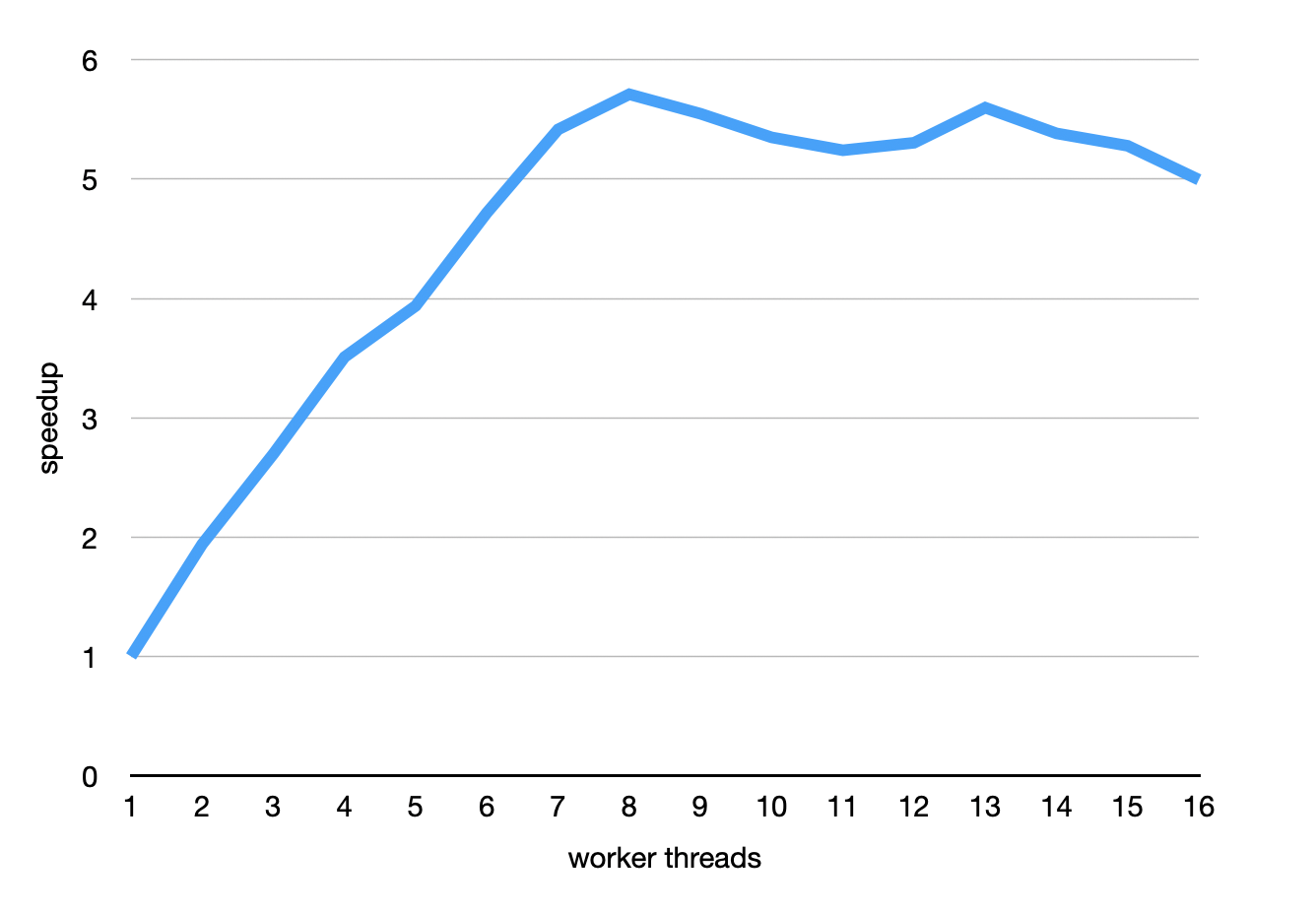
Examining the speedup as the number of threads vary tells us about the parallel program’s scalability. If a program gets N× faster when we use N threads, that’s great scalability. When it doesn’t quite hit that ideal, that’s reality—no real software scales perfectly forever.
The chart here shows us that this program scales very well up to 8 threads. The 2-thread exaction is 1.94× faster than the 1-thread version, which is really close to 2. Things slowly deteriorate a little, and the 6-thread version is only 4.72× faster than the 1-thread version. That means this program scales very well but not quite perfectly.
Comparing to a Single Thread
If you measure only scalability, you can miss a really important pitfall in parallel programming: just adding parallelism can come at a cost. It is always therefore important to compare your 1-thread parallel program with a simple sequential baseline.
Her’s a simple plot comparing a plain, sequential primality checker with 1-worker version of our producer-consumer implementation:
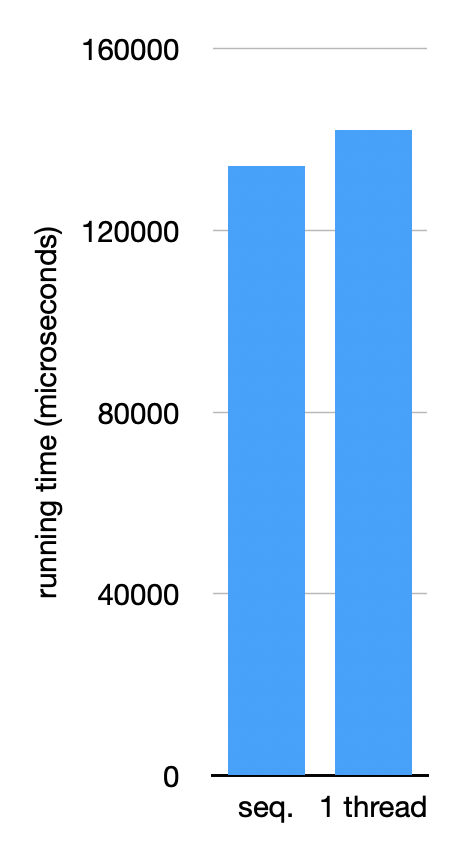
In this program, the parallel setup costs something, but not a lot. This also makes sense: there is a cost to allocating and coordinating the bounded buffer, and the producer/consumer setup inherently involves some overhead for synchronization. But most of the work is spent on actually running the primality check, so that dominates the running time.
But the cost is not always so small. For an entertaining read about parallel systems that are hilariously slower than sequenial ones, I recommend the 2015 paper “Scalability! But at what COST?”.
Modeling Parallel Performance
The reason this program scales so well is because the problem it’s solving is embarrassingly parallel. An embarrassingly parallel problem is one where you can break it down into completely independent chunks and solve the chunks in isolation, without every communicating between those chunks. Checking whether a single number is prime is a completely independent, isolated piece of work. There is no need for two threads processing different numbers to ever coordinate.
There are many embarrassingly parallel problems in the world, but there are just as many problems that are more difficult to parallelize. It can be useful to generalize the “embarrassingly parallel” concept to characterize how parallelizable a given program is. Imagine two extremes on a spectrum:
- On one side, there are purely sequential programs: ones that need to run on a single thread, and no parallelism can ever offer any speedup.
- On the other side, there are embarrassingly parallel programs: ones where it is trivial to divide up work, and you can roughly expect perfect scalability. In other words, n threads lead to a speedup of roughly n in this ideal case.
All real programs lie somewhere on this spectrum. A common tool for understanding the potential benefit of parallelization is Amdahl’s law. It consists of this formula:
speedup=11−p+ps
where p is the fraction of the program that can be parallelized and s is the amount of parallelism you use. So for a completely sequential program, p=0, and for a perfectly embarrassingly parallel program, p=1.
One important takeaway from Amdahl’s law is that surprisingly tiny non-parallelizable parts of programs can totally ruin their scalability. For example, imagine that 5% of your program needs to run sequentially, so p=0.95. With 2 threads, the results are not so bad: Amdahl’s law predicts a 1.9× speedup. But with 16 threads, the speedup is only 9.1×. Even for a 99% parallel program, if you scale to a 192-core machine, the law predicts a speedup of only 66×.
Implementing printf
Instructions:
Remember, all assignments in CS 3410 are individual.
You must submit work that is 100% your own.
Remember to ask for help from the CS 3410 staff in office hours or on Ed!
If you discuss the assignment with anyone else, be careful not to share your actual work, and include an acknowledgment of the discussion in a collaboration.txt file along with your submission.
The assignment is due via Gradescope at 11:59pm on the due date indicated on the schedule.
Submission Requirements
You will submit your completed solution to this assignment to Gradescope. You must submit:
my_printf.c, which will be modified with your solution for Task 1 and Task 2test_my_printf.c, which will contain your tests for your solution for Task 1 and Task 2
Restrictions
- You may not include any libraries beyond what is already included in
my_printf.h - Your solution should use constant space (you should not use arrays, either dynamically or statically)
- You may add as many helper functions as you would like in
my_printf.c, but you must leave the function signatures formy_printfandprint_integerunchanged. You may not changemy_printf.h, as we will be using our own header file for grading.
Provided Files
The provided release code contains four files:
my_printf.h, which is a header file that contains the required function definitions and some useful include statements. You may not modify this file. You may also not include any libraries in your implementation beyond what is included in already in this file.my_printf.c, which contains the function definitions for your implementation. This is where you will write your code formy_printfandprint_integer.test_my_printf.c, which is a test file with a couple test cases to get you started. You must add more tests to receive full credit for this assignment.test_my_printf.txt, which is a text file that you can use to compare your outputs to by “diff” testing. See more in Running and Testing.
Getting Started
To get started, obtain the release code by cloning the a1 repository from GitHub:
$ git clone git@github.coecis.cornell.edu:cs3410-2024fa/<YOUR NET ID>_printf.git
- Note: Please replace the
<YOUR_NET_ID>with your netid. For example, if you netid iszw669, then this clone statement would begit clone git@github.coecis.cornell.edu:cs3410-2024fa/zw669_printf.git
Overview
In this assignment you will implement your own version of printf (see the
documentation here) called
my_printf without relying on the C standard library. Recall that printf works
by taking in a format string that contains various format codes, in addition
to a variable number of other arguments. The format codes specify how to “plug in”
the arguments into the format string, to get the final result. For example:
printf("I love %d!", 3410); // prints "I love 3410!"
printf("Hello, %s", "Alan"); // prints "Hello, Alan"
printf("Hello %s and %s!", "Alan", "Alonzo"); // prints "Hello Alan and Alonzo!"
You will implement two key functions:
print_integer(int n, int radix, char *prefix): Print the integerntostdoutin the specified base (radix), withprefiximmediately before the first digit.my_printf(char *format, ...): Print a format string with any format codes replaced by the respective additional arguments.
Your implementation will be contained in my_printf.c. We’ve provided you with the
function signatures to get you started. You should look at my_printf.h for detailed
function specifications.
Assignment Outline
- Task 0: You will complete Task 0 in lab. This task is meant to build familiarity with the course tools and C as well as get you started on Task 1
- Task 1: You will implement the
print_integerfunction - Task 2: You will implement the
my_printffunction
Implementation
(Lab) Task 0: Intro to C and print_integer helper functions
View the lab slides here.
Before coming to lab, make sure to go through the course setup materials for git and the RISC-V Infrastructure. The lab tasks will assume you have at least set up your Cornell GitHub credentials and have your favorite text editor, such as Visual Studio Code, ready to go.
Step 1: Compiling and running C programs
Course Docker Container
Follow these instructions to set up Docker and obtain CS 3410’s Docker container. To summarize, you will need to:
- Install Docker itself.
- Download the image with
docker pull ghcr.io/sampsyo/cs3410-infra. - Consider setting up an
rvalias to make the container easy to use.
If you don’t already have a favorite text editor, now would also be a good time to install VSCode.
C Programming
Next, follow these instructions for writing, compiling, and running your first C program.
When your program runs, show the result to a TA. Congratulations! You’re now a C programmer.
Git
Now, we’ll get some experience with git! If you haven’t already, be sure to follow our guide to setting up your credentials on GitHub so you have an SSH key in place.
Go to the to the Cornell GitHub website and create a repository called “lab1”. This repository can be public, but for assignments all of your repositories must be private.
Now, clone your repository from within the cs3410 directory you made earlier:
$ git clone git@github.coecis.cornell.edu:abc123/lab1.git
replacing abc123 with your actual NetID. If this doesn’t work, ask a TA for
assistance. There is probably something wrong with your GitHub configuration.
Before changing directories into the
repo, you should move your hi.c file that you created during the Docker setup step into the lab1 folder and clean up the executables
we made earlier:
$ mv hi.c lab1
$ rm a.out
$ cd lab1
$ ls
If you haven’t created one yet, just do:
$ cd lab1
$ printf '#include <stdio.h>\nint main() { printf("hi!\\n"); }\n' > hi.c
You should see the file hi.c in your repository. Enter:
$ git status
The following should appear (or something like it):
On branch main
No commits yet
Untracked files:
(use "git add <file>..." to include in what will be committed)
hi.c
Now, you should add the file hi.c to stage it, make a commit, and then
push to the remote repository:
$ git add hi.c
$ git commit -m "Initial commit"
$ git push
This is commonly the GitHub workflow for a single person working on an assignment. You’ll make some changes, commit them, and push them, over and over until you finish the assignment.
To learn more about git, consider following our complete git tutorial!
Step 2: print_digit and print_string
For this next task, you are going to write two helper functions to help you in Task 1 and Task 2 of this assignment:
print_digit(int digit): Given an integer, print it to the terminal (without usingprintf)print_string(char* s): Given a string, print it to the terminal (without usingprintf)
You do not need to submit lab1.c for A1. If you would like to use the print_digit and print_string functions as part of your implementation, you should copy and paste them into my_printf.c.
First, cd into your lab1 repository. Then, make a file called lab1.c, and
copy/paste the following code:
#include <stdio.h>
// LAB TASK: Implement print_digit
void print_digit(int digit) {
}
// LAB TASK: Implement print_string
void print_string(char* s) {
}
int main(int argc, char* argv[]) {
printf("print_digit test: \n"); // Not to use this in A1
for (int i = 0; i <= 16; ++i) {
print_digit(i);
fputc(' ', stdout);
}
printf("\nprint_string test: \n"); // Not to use this in A1
char* str = "Hello, 3410\n";
print_string(str);
return 0;
}
Hint: For print_digit, you’ll want to use an ASCII table.
Save the file and exit the editor. Now is a good time to commit and push your changes to your repository. Once you’ve pushed, try to implement the functions print_digit and print_string. The TAs are available for help should you need it.
Once you’ve implemented the functions, you can run the program:
$ rv gcc -Wall -Wextra -Wpedantic -Wshadow -std=c17 -o test_lab1 lab1.c
$ rv qemu test_lab1
Remember, if you change lab1.c between runs, you need to recompile the program.
That’s all for this lab!
Task 1: print_integer
For Task 1 and Task 2, all your code should be in the “a1” Git repository. See the Getting Started section for how to retrieve the starter code. Your implementation will be contained in my_printf.c and test_my_printf.c.
The print_integer function takes a number, a target base, and a prefix string and prints the
number in the target base with the prefix string immediately before the first
digit to stdout. radix may be any integer between 2 and 16 inclusive. For
values of radix above 10, use lowercase letters to represent the digits
following 9 (since bases higher than 10 cannonically use lowercase letters as
well).
This function should not print a newline. Here are some examples:
print_integer(3410, 10, "")should print “3410”print_integer(-3410, 10, "")should print “-3410”print_integer(-3410, 10, "$")should print “-$3410”print_integer(3410, 16, "")should print “d52”print_integer(3410, 16, "0x")should print “0xd52”print_integer(-3410, 2, "0b")should print “0b11111111111111111111001010101110”print_integer(-3410, 16, "0x")should print “0xfffff2ae”
For the radix 10, negative numbers should be printed with a negative sign (-).
All other bases should use the 2’s complement representation from lecture. In
other words, it should not print a negative sign, and instead just print
an unsigned integer representing a 2’s complement number. This is exactly what
printf from the standard library does when you pass in negative integers for
bases other than 10. You can try this on your own:
#include <stdio.h>
int main() {
printf("-10 in hex is: %x\n", -10);
printf("-10 in binary is: %b\n", -10); // Note: requires C23
}
The above code outputs:
-10 in hex is: fffffff6
-10 in binary is: 11111111111111111111111111110110
which is the 2’s complement representation of -10 in hex and binary, respectively.
You are not allowed to call any functions from the C standard library except for fputc anywhere in your implementation.
You should print a character to the console using fputc(c, stdout), where c is the character you want to print.
Tip: In addition to the documentation on cppreference.com, you can also find documentation for many standard library functions in C through the manual pages (“manpages”) in your terminal. Simply type:
$ man fputc
to pull it up. You can scroll through it and then type q to exit.
You must not make any assumptions about the size of an integer on a
given platform. On our platform, an integer is 32 bits, but C allows int to
be different sizes on different platforms. For example, on some architectures
int is 64 bits. Thus, you cannot store the new representation of the integer as a string or in a buffer of any size, as this would make assumptions about how big an integer is on your platform. Calling malloc is also prohibited
(by extension of the fact that stdlib.h is prohibited). In other words, you
should figure out how to do this without using any additional memory.
Storing characters or integers in an array (dynamically or statically) will result in a significant deduction.
You’ll also need to figure out how to print the integer from left-to-right instead of right-to-left without using additional memory. One of the algorithms you might recall from class for changing the base of a number would give you the digits from right-to-left, so it can seem tempting to try to use this as a starting point. Be warned that this will not work, as any tricks such as “reversing” the output or storing the digits would violate the constraints of this assignment (i.e. no standard library usage and no storing values in an array). Instead, think of how you can work backwards from the methods you’ve learned in class.
Task 2: my_printf
This function prints format with any format codes replaced by the respective
additional arguments, as specified below:
Your my_printf function is required to support the following format codes:
%d: integer (int,short, orchar), expressed in decimal notation, with no prefix.%x: integer (int,short, orchar), expressed in hexadecimal notation with the prefix “0x”. Lowercase letters are used for digits beyond 9%b: integer (int,short, orchar), expressed in binary notation with the prefix “0b”.%s: string (char*)%c: character (int,short, orchar, between 0 and 127) expressed as its corresponding ASCII character%%: a single percent sign (no parameter)
For each occurrence of any of the above codes, your program shall print one of
the arguments (after the format) to my_printf(...) in the specified format.
Anything else in the format string should be expressed as is. For example, if
the format string included "%z", then "%z" would be printed. Likewise, a lone
“%” at the end of the string would also be printed as is (note that this differs
slightly from the behavior of printf).
Note that strings in C can be NULL. If my_printf is passed a null string
as an argument, it should not crash, but instead print (null) to represent the
would-be string:
#include <stdio.h>
int main(int argc, char* argv[]) {
my_printf("Null string: %s", NULL); // Prints: "Null string: (null)"
}
Again, you are not allowed to call any C standard library functions. You
should print to stdout only using fputc (documentation for fputc is here).
For any format codes relating to numbers, your program should handle any valid
int values between INT_MIN and INT_MAX, inclusive.
Note that my_printf is a variadic function, meaning it takes in a variable
number of arguments. You don’t need to know this deeply, but you will
need to look up the syntax, and also understand how a program determines the
number of arguments.
A variadic function is any function that takes in an unknown number of optional
parameters. The optional parameters are represented by three dots (e.g. int foo(int n, ...)).
The dots are a part of the C language. The optional arguments are accessed using
va_arg from stdarg.h. You must call va_start at the start of your
variadic function before the first use of va_arg. You must call va_end once
at the end of your variadic function, after the last use of va_arg. There is
no way to know from va_arg how many optional arguments there are, so you
need to use some other information to determine how many times to call va_arg.
In this case, it is the format string. Here’s an example from the GNU
documentation:
#include <stdarg.h>
#include <stdio.h>
int add_em_up(int count,...) {
va_list ap;
va_start (ap, count); /* Initialize the argument list. */
int sum = 0;
for (int i = 0; i < count; i++)
sum += va_arg (ap, int); /* Get the next argument value. */
va_end (ap); /* Clean up. */
return sum;
}
int main(int argc, char* argv[]) {
/* This call prints 16. */
printf("%d\n", add_em_up (3, 5, 5, 6));
/* This call prints 55. */
printf("%d\n", add_em_up (10, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10));
return 0;
}
Here are some examples to help you understand the spec:
my_printf("3410")should print “3410”my_printf("My favorite class is %d", 3410)should print “My favorite class is 3410”my_printf("%d in hex is %x", 3410, 3410)should print “3410 in hex is 0xd52”my_printf("The pass rate in 3410 is 100%%")should print “The pass rate in 3410 is 100%”my_printf("Professor %s and Professor %s are the instructors ", "Sampson", "Guidi")should print “Professor Sampson and Professor Guidi are the instructors”
Note that insufficient parameters could lead to undefined behavior (i.e. when the number of arguments is less than the number of format codes). You do not have to handle this case. Similarly, mismatched parameters (when the format code does not match the given argument’s type) can also lead to undefined behavior, but you do not need to handle this.
You are encouraged to use print_integer in my_printf.
Nonetheless, these functions will be tested independently.
Running and Testing
To compile your code, run:
rv gcc -Wall -Wextra -Wpedantic -Wshadow -std=c17 -o test_my_printf test_my_printf.c my_printf.c
Then, to run your code:
rv qemu test_my_printf
Like many commands on this page, this assumes you have the rv aliases setup as described in our RISC-V Infrastructure setup guide.
We will be testing your code by comparing the output of your program to a test
file. You will extend the file test_my_printf.txt with your own
test cases. You are required to write more tests, and the quality of the tests
will be graded. Feel free to use the examples in this handout as a starting
point.
To receive full credit for testing, you should have at least 10 test cases
each for print_integer and my_printf. Test cases should cover as many
paths through your code as possible. To receive full credit for testing for print_integer,
you should have at least:
- One test representing integers for each base from 2-16
- One or more tests for different prefixes
- One or more tests with no prefixes
To receive full credit for testing my_printf you should have at least:
- One test for each format code
- One test for no format codes
- One test that contains multiple format codes
To compare the output of your program with the test file, run:
rv qemu test_my_printf > out.txt && diff out.txt test_my_printf.txt
If you don’t see any output from this command, your tests are passing. Note,
for each test you add in test_my_printf.txt, you must call the corresponding
function (either print_integer or my_printf) in test_my_printf.c. You
should insert newlines between your test cases for readability. You may use
printf in your test file, if you wish.
Don’t forget to recompile your code between different runs of your program.
Note, you can do this all in one command, like such:
rv gcc -Wall -Wextra -Wpedantic -Wshadow -std=c17 -o test_my_printf test_my_printf.c my_printf.c && \
rv qemu test_my_printf > out.txt && \
diff out.txt test_my_printf.txt
Submission
Submit my_printf.c and test_my_printf.c to Gradescope.
Upon submission, we will provide a sanity check to ensure your code compiles and passes the public test cases.
Rubric
- 40 points:
print_integercorrectness - 50 points:
my_printfcorrectness - 10 points: test quality
Minifloat
Instructions:
Remember, all assignments in CS 3410 are individual.
You must submit work that is 100% your own.
Remember to ask for help from the CS 3410 staff in office hours or on Ed!
If you discuss the assignment with anyone else, be careful not to share your actual work, and include an acknowledgment of the discussion in a collaboration.txt file along with your submission.
The assignment is due via Gradescope at 11:59pm on the due date indicated on the schedule.
Submission Requirements
For this assignment, you will need to submit the following five files:
minifloat.c, with your written implementation for the missing functions.minifloat_test_part1.expected, to match additional tests added inminifloat_test_part1.c- Some additional tests, in:
minifloat_test_part1.cminifloat_test_part2.cminifloat_test_part3.c
Restrictions
For this assignment, you will be working with building your own floating-point representation.
- You may not use built-in C operations for floating-point arithmetic.
- You may not cast data to
floatordouble, or create variables with these types.
Provided Files
The provided release code contains seven files:
minifloat.c, which includes some completed functions and some functions you are expected to implementminifloat.h, which provides declarations and comments for the functions inminifloat.c, including those you are to implementminifloat_test_part1.c,minifloat_test_part2.c,minifloat_test_part3.c, which provide some tests for you to get started. You are expected to add more tests of your own to each of these test suitesminifloat_test_part1.expected, which provides a baseline file to help with testing part 1. You are expected to add more lines to this file as part of testing part 1.Makefile, which provides structure to compile your code (see our brief tutorial on Makefiles)
Getting Started
To get started, obtain the release code by cloning your assignment repository from GitHub:
$ git clone git@github.coecis.cornell.edu:cs3410-2024fa/<NETID>_minifloat.git
Replace <NETID> with your NetID. For example, if your NetID is zw669, then this clone statement would be git clone git@github.coecis.cornell.edu:cs3410-2024fa/zw669_minifloat.git
Overview
In this assignment, you will be developing a custom minifloat data format in C. You will be expected to reason about floating-point details and to implement C functions.
Background
In class, we learned about floating-point numbers, which represent decimals with some number of bits.
C has built-in float and double types, which use (on modern hardware)
32 bits and 64 bits, respectively.
Increasing the number of bits in a floating-point representation gives it more precision and more dynamic range, at the expense of less efficient arithmetic.
It can also be useful, however, to perform operations with smaller floating-point representations—trading off precision for potentially faster calculations.
In this assignment, you will implement functions for a specialized 8-bit floating-point type. We’ll call these 8-bit numbers minifloats. Minifloats have severely limited precision, but such tiny floating point values are useful for situations where errors matter less and data sizes are enormous: most prominently, in machine learning. See, for example, this paper and this other paper that both show serious efficiency advantages from using 8-bit minifloats. While most floating point formats enjoy built-in hardware support, we can also implement minifloats in software with bit packing tricks.
Minifloats follow a similar representation strategy to the standard IEEE floating-point types that we learned about in lecture. However, they differ in a few important ways to make the implementation simpler, which we will summarize as well.
Minifloat specification
- Minifloats use 8 bits in total: 1 sign bit, 3 exponent bits, and 4 significand bits. The layout of a minifloat looks like this, with
sfor sign,efor exponent, andgfor significand:
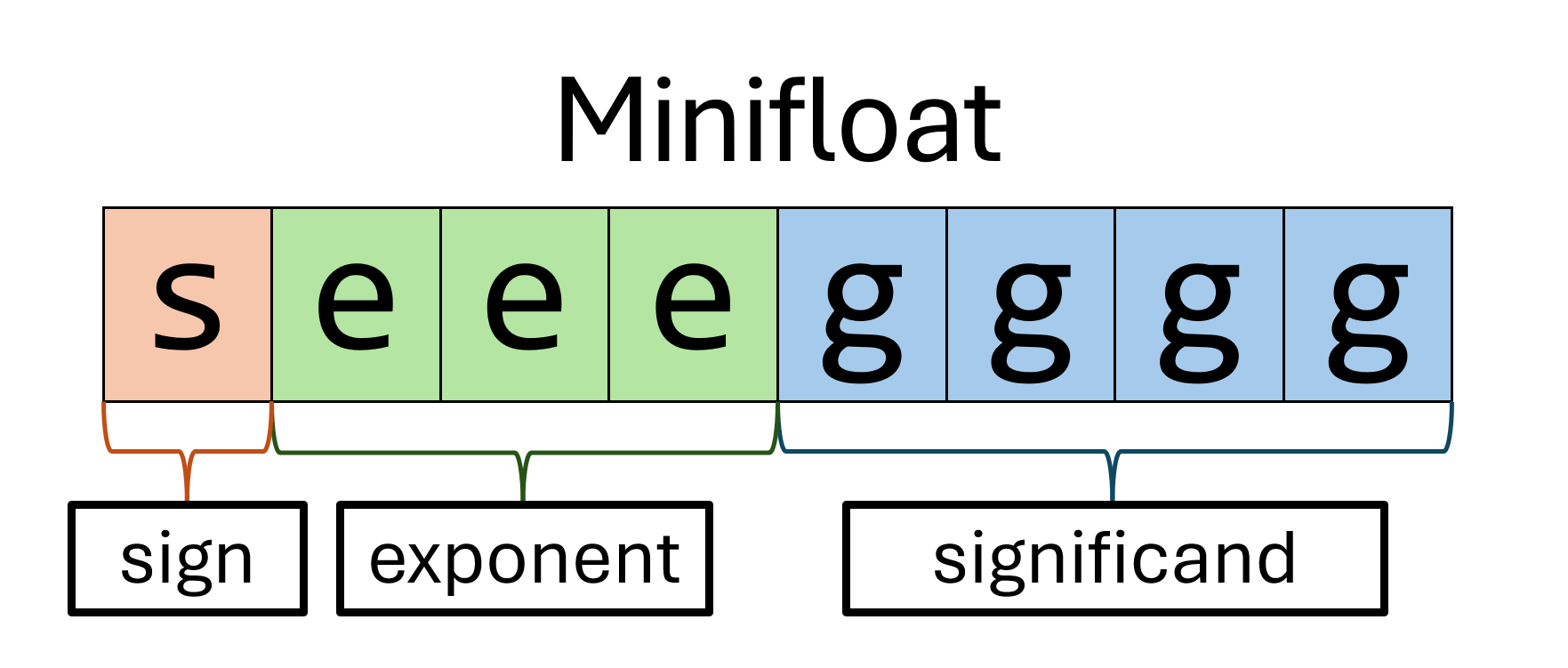
-
As in standard formats, a sign bit of
0indicates a positive number, and a sign bit of1indicates a negative number. -
Minifloats have a bias of 3. In other words, we subtract 3 from the bit-representation of a minifloat exponent.
-
Unlike standard floating-point formats, wherein we usually append a leading 1 to the significand bits with the 1.g notation, minifloats use the significand directly, with the binary point after the first digit. So if the four significand bits are g3g2g1g0, then the “base” part of the represented value is the binary number g3.g2g1g0. Or, in other words, the value is g×2−3, where g is the unsigned integer value of those 4 bits.
-
Also unlike standard floating-point formats, our minifloats do not use special values: not a number (NaN) and infinity (+∞ and -∞).
All together, the value represented by a minifloat with sign s, exponent e, and significand g is:
(−1)s×(g×2−3)×2e−3
Or, equivalently, if you prefer to think of the significand’s representation in terms of bits:
(−1)s×(g3.g2g1g0)×2e−3
where g3 is the significand’s most significant bit, g0 is the least significant bit, and so on.
Minifloat Examples
To help with reading a minifloat, here are a pair of example calculations of reading a minifloat as a base-10 decimal:
Example 1: 10111100
We have a sign of 1, an exponent of 011, and a significand of 1100.
- Our sign
1corresponds to −1. - Our exponent
011corresponds to a decimal exponent of 3−3=0. (We’re applying our −3 bias here.) - Our significand
1100corresponds to the decimal 12×2−3=128=1.5. (Or, equivalently, the significand corresponds to the binary number 1.1002, which is 1.5 in decimal.)
In total, our number is then −1×1.5×20=−1×1.5×1=−1.5.
Example 2: 00010010
We have a sign of 0, an exponent of 001, and a significand of 0010.
- Our sign
0corresponds to +1. - Our exponent
001corresponds to a decimal exponent of 1−3=−2. - Our significand
0010corresponds indicates the binary value 0.0102, which equals 0.2510.
In total, our number is then 1×0.25×2−2=116=0.0625.
Bit size in C
We want to ensure that the type we are using to represent a minifloat is exactly 8 bits.
We will use the uint8_t type from C’s stdint.h header.
(We will avoid char, even though char is 8 bits on most platforms, because C unhelpfully does not guarantee that is is exactly 8 bits everywhere.)
To break down this type’s, the uint means that bit-level operations are as on an unsigned integer, the 8 means that we expect operations to be on 8 bits, and _t is a common naming convention that indicates that this is a type.
The stdint.h header defines many similar types, like these:
| Type | Description |
|---|---|
| uint8_t | unsigned integer with 8 bits |
| uint16_t | unsigned integer with 16 bits |
| int8_t | signed integer with 8 bits |
Your Task
This assignment is divided into three parts: displaying minifloats as decimals, implementing operations on minifloats, and using minifloats. Each part will have you implementing 1–3 functions, and adding test cases to help convince yourself these functions are correct. You must add at least 4 new test cases per function to what we have provided, though you may add more.
For all of your C implementations, you may not include any constants or variables of type float, double, or long double.
You may not use C’s built-in floating-point operations, such as + on floating-point values.
This is not an arbitrary restriction. Using a larger float representation in your implementation will defeat the purpose of the smaller representation, which is that they are smaller and faster than “normal” floating-point types. Because of floating-point error, it is also very likely to introduce incorrect results.
We have provided a mini_to_double utility function to help you with debugging and testing. You may not use this function in any of your submitted implementations, but you may use this function for writing test cases for any of your functions.
Part 0: Lab
View the lab slides here.
In this lab, you will gain practice using floating point numbers. There are 2 designated checkoff points where you should show your work to a TA.
Review
If you need to, look over the lecture notes on standard floating-point types to remind yourself of the basic principles. And try out float.exposed to get hands-on practice!
Read over the background above and especially the specification for minifloats. To briefly summarize the minifloat format:
- Bit 7 is the sign bit
- Bits 6–4 are the exponent bits
- Bits 3–0 are the fraction bits
(Bits are numbered from the right, so 0 is the least significant bit.)
Part 0.1: Practice Conversions
Decimal to float. To convert from a decimal to a floating point number:
- Convert the integer and fractional parts into binary.
- Combine the results and shift accordingly.
- Convert our exponent into biased form.
- Convert the fractional part into a mantissa/significand.
- Recombine for a final floating-point representation.
Here’s a 32-bit example. Consider the decimal 12.375.
Converting the integer portion into binary yields 1100.
Converting the fractional part is a little more labor intensive. Our fractional part is 0.375. To convert, multiply the fractional part by 2, record the integer part of the result (should be 0 or 1), and repeat with the new fractional part until the fractional part becomes 0 or the precision limit is reached (is 23 digits for the IEEE 754 32-bit format). The recorded integer parts of this process becomes our binary representation for the original fractional part.
- 0.375×2=0.750. Record
0. - 0.750×2=1.500. Record
1. - 0.500×2=1.000. Record
1.
Thus our binary representation of 0.375 is 011, and thus our binary
representation of 12.375 is 1100.011.
We now normalize our result so that it fits the format (1.xyz…)×2e. In this case, we shift to the right to obtain 1.100011×23.
Next, we need to apply our format’s exponent bias, which for this format is 127. To bias the exponent, we add our original exponent with the bias. In our example, this gives us 3 + 127 = 130.
From here, we can see that:
- The biased exponent form of 130 yields
10000010in binary. - The fractional part is 1000112, and thus our mantissa is
10001100000000000000000. (We fill in the remaining digits with 0s.) - We have a positive number, so our sign bit is
0.
(The reason the exponent’s “bias” of 127 exists is so that we can represent both positive and negative exponents using an unsigned integer. It may help to think of the bias as the reference point of no shifting (an exponent of 0), and any additions and subtractions to this bias represent how much we shift by. To find the to find the bias of any floating-point number, we can use the formula 2(k−1)−1 where k is the number of bits in the exponent field.)
Thus, our final floating point representation is 0 10000010 10001100000000000000000.
You can try checking the answer by entering these bits into float.exposed if you like.
Float to decimal. To convert from a floating-point number to a decimal number:
- Separate out the sign, exponent, and mantissa.
- We restore the 1. back to the mantissa and drop the trailing 0s.
- We de-normalize the number so the exponent is 0.
- Convert the integer and fractional parts to decimals.
- Add a negative sign if necessary.
Exercises:
- Convert -4.75 to our 8-bit floating point format.
- Convert 1.7 to our 8-bit floating point format.
- Convert the binary float 11010011 to a decimal.
- Convert the binary float 00100110 to a decimal.
Checkoff #1: Show your converted numbers to a TA.
Part 0.2: Floating Point Addition and Inaccuracies
You can perform many arithmetic operations with floating-point numbers. However, in this lab, you will be practicing with addition as an introduction to floating-point arithmetic.
To perform addition with a floating point number:
- Rewrite the smaller number so that the exponents are equal, and adjust the mantissa of the number with the smaller exponent by shifting it to the right accordingly.
- Add the mantissas together.
- Recombine and renormalize the result if necessary.
Exercises:
- Add 0.25 and 8.0 with our 8-bit minifloat format.
- Add 1.25 and 2.5 with our 8-bit minifloat format.
- Can you find two numbers that share the same nearest minifloat representation?
- What is the largest number our minifloat format can represent?
Take note of where accuracy was lost in these calculations. Why are our results so far off from what we expect?
Checkoff #2: Show your addition results to a TA.
Part 1: Displaying Minifloats
Your first task is to implement a function for displaying minifloats in C, named print_mini. This function takes in a minifloat and must print the sign, whole number, and fractional part associated with this minifloat as a base-10 value. The exact specification, with examples, is given in minifloat.h. Your implementation should be filled into minifloat.c.
To make your task somewhat easier, we have written a concrete call to printf at the end of the each function that you may use as a guide for what to implement. Note that print_mini requires that we write 6 decimal digits—the provided printf specifier %06d will fill any integer to have preceding zeros such that the printed integer has 6 digits. To provide two concrete examples:
printf("%06d", 123)will print000123printf("%06d", 100000)will print100000
Remember, you may not include any constants or variables of type float, double, or long double, and you may not use any floating-point operations.
You may, however, use any integer arithmetic operation (including integer division and modulus).
In C, dividing two integers with i / j produces an integer.
But be sure not to include a double constant (such as 1.0) by accident.
Hint: You may find it useful to observe that 1/64=0.015625, and that, with integer division, 1000000/64=15625.
Testing Part 1
A test script to help guide your development can be found in minifloat_test_part1.c. You can build this test with the following command:
rv make part1
To test this code, you must execute the resulting .out file and pipe your print results to a file, such as with the following command:
rv qemu minifloat_test_part1.out > minifloat_test_part1.txt
Reminder: use the rv aliases for each command if you have it set up!
Finally, you must compare the resulting prints to our expected results using diff:
diff minifloat_test_part1.txt minifloat_test_part1.expected
If you observe any differences between the two, a printing test failed.
You can also combine these operations into a single bash command:
rv make part1 && rv qemu minifloat_test_part1.out > minifloat_test_part1.txt && diff minifloat_test_part1.txt minifloat_test_part1.expected
Reminder: You must add 4 new printing tests (which means modifying both minifloat_test_part1.c and minifloat_test_part1.expected).
Part 2: Minifloat Operations
Your second task is to implement an equality check, addition, and multiplication between minifloats. Specifically, you will be implementing mini_eq, mini_add, and mini_mul, which both take in two minifloats and produce a new minifloat. As before, the specifications for each function can be found in minifloat.h, and your implementation should be written in minifloat.c.
The results of the arithmetic operations mini_add and mini_mul must produce the minifloat value closest to adding together the corresponding real numbers. If there are two possible closest real numbers, your implementation must correspond to the closest real number further from zero than the result of addition. For example, we would round 2.125 to 2.25, and similarly -1.0625 to -1.125.
If there are multiple possible minifloat representations of the resulting real number, you must return the minifloat with the smallest exponent. For example, the minifloat value 0 011 0010 could be equivalently represented as 0 001 1000, and only the latter is considered correct for these arithmetic operations. Additionally, if an arithmetic operation would return 0, you must return exactly 00000000.
If applying addition or multiplication would result in a real number larger or smaller than can be represented by a minifloat, the result of these operations is undefined, and need not be tested.
Hint: If you become stuck on any of these functions, consider attempting another—each requires detail that can become more obvious while working on another.
Testing Part 2
Testing minifloat operations is more straightforward than testing the printing implemented earlier. We can simply run each test file and compare the resulting minifloats to expected values. To test part 2, you can directly build and execute part2:
rv make part2 && rv qemu minifloat_test_part2.out
Reminder: You must add 4 new tests per function.
Hint: Write as many edge-case tests as you can think of, there are many potential tricks with negative numbers and very small or very large minifloats.
Part 3: Using Minifloats
Your third task is a straightforward example use of the minifloats you have implemented. Specifically, you’ll be implementing functions to calculate the volume and surface area of a cylinder in the functions titled cylinder_volume and cylinder_area.
The volume and surface area of a cylinder depends on two variables, the radius r and height h of the cylinder, by the following equations:
- volume=π×r×r×h
- surface area=2×π×r×(h+r)
For reference and comparison, we have also written an implementation of these functions double_cylinder_volume and double_cylinder_area. These may be useful to refer to while implementing your own function, but are also used for the written task below.
For these implementations, you are expected to use the constant minifloat representation of PI to be 01001101 (representing 3.25), which is the closest minifloat to the decimal π≈3.14159. We have included this constant definition in minifloat.c for your convenience.
Testing Part 3
To test part 3, you can directly build and execute part3:
rv make part3 && rv qemu minifloat_test_part3.out
We have only provided you with a single simple test for each, and you should write at least 4 new tests. We test these particular functions by comparing our minifloat calculation to the result produced by calculating the same value with a double. We expect that the minifloat result (being less accurate) will have some error compared to the double representation, which in the test is represented by the threshold parameter.
We recommend trying out a few operations and seeing how difference there is between minifloat and double calculations, and adjusting your threshold accordingly. To help with comparing these operations, we use the provided mini_to_double utility function to calculate calculate a double value before and after computing the minifloat equivalent.
(We do not define a double_to_mini conversion.)
The mini_to_double utility is only for testing.
Do not use it in your main implementation.
Remember that your goal is to implement minifloat operations “from scratch,” using only integer arithmetic.
This is what makes minifloats more efficient than float or double.
Your tests should not include cases where the minifloat arithmetic would overflow (produce a result larger than the maximum minifloat or smaller than the largest negative minifloat). We do not define the results of these overflowing operations.
Submission
Submit minifloat.c, minifloat_test_part1.expected, minifloat_test_part1.c, minifloat_test_part2.c, and minifloat_test_part3.c to Gradescope.
Upon submission, we will provide a sanity check to ensure your code compiles and passes the public test cases.
Rubric
- 16 points:
print_minicorrectness - 18 points:
mini_eqcorrectness - 16 points:
mini_addcorrectness - 19 points:
mini_mulcorrectness - 8 points:
cylinder_areacorrectness - 8 points:
cylinder_volumecorrectness - 15 points: test quality
Huffman Compression
Instructions:
Remember, all assignments in CS 3410 are individual.
You must submit work that is 100% your own.
Remember to ask for help from the CS 3410 staff in office hours or on Ed!
If you discuss the assignment with anyone else, be careful not to share your actual work, and include an acknowledgment of the discussion in a collaboration.txt file along with your submission.
The assignment is due via Gradescope at 11:59pm on the due date indicated on the schedule.
Submission Requirements
You will submit your completed solution to this assignment on Gradescope. You must submit:
huffman.c, which will contain part of your work for Task 0 and all of your work for Tasks 1 and Task 2.priority_queue.c, which will contain part of your work for Task 0.
Restrictions
- You may not modify any files other than
huffman.candpriority_queue.c. You won’t be submitting them anyway
Provided Files
priority_queue.h, which is a header file that defines the specification for the priority queue.priority_queue.c, which will contain your implementation of a priority queue and stack. You will modify this file.huffman.h, which is a header file that defines the types and functions you will need to implement Huffman compression.huffman.c, which will contain your implementation for the Huffman compression system. You will also modify this one.bit_tools.h, which is a header file that defines theBitWriterandBitReaderstructs and their respective functions for reading and writing binary values from files.bit_tools.c, which contains the implementation of the functions forBitWriterandBitReader.utils.h, which contains utility functions for printing lists and tree nodes.utils.c, which contains the implementation for the utility functions.Makefile, which contains the build tools for this assignment.test_priority_queue.c, which contains functions to test your implementation for Task 0. You may add tests here, but you will not turn this file in.test_huffman.c, which contains functions to test your implementation for Task 1. You may also modify this file, as above.cu_unit.h, which contains the macro definitions that you’ll use for unit testing.
Remember, do not modify other source files except the ones containing your implementation. We will grade your submission with “stock” versions of the supporting files.
Overview
In this assignment you will implement a data compression system using Huffman coding. Huffman compression is an encoding scheme that uses fewer bits to encode more frequently appearing characters and more bits to encode less frequently appearing characters. It is used by ZIP files, among many other things. The high-level overview of the algorithm is:
- Calculate the frequency of each character in the data. (Task 0)
- Build a Huffman tree using the frequencies. (Task 1)
- Build an encoding table using the Huffman tree. (Task 2)
- Encode each character in the data using your encoding table. (Task 2)
In the lab, you will implement a priority queue in C. You’ll use this to build your Huffman tree. The bulk of the work for this assignment will come from understanding the Huffman coding algorithm and manipulating data structures in C.
Huffman Compression Algorithm
Your implementation will read a single text file as input and produce two output files: a compressed data file and a coding table file that encodes enough information to allow decompression. (This assignment does not include decompression; we have given you a decompressor implementation.) Task 2 describes the format for these files.
Before moving onto the tasks, let’s break down the Huffman compression algorithm. You may recall that ASCII is a straightforward way to represent characters. In ASCII, every character is encoded with 8 bits (1 byte). There are 256 possible ASCII values that can be represented. This means that if we use standard ASCII encodings to represent a text file, each character in the file requires exactly 1 byte. This is inefficient, as most text streams don’t actually use all 256 possible characters. The basic idea behind Huffman encoding is as follows: use fewer bits to represent characters that occur more frequently.
Consider the string go go gophers.
Because g and o appear so much more often, can we construct an encoding that uses a small number of bits for these characters, and possibly a larger number of bits for characters like h?
That’s the goal with Huffman coding.
The core data structure we need is a binary tree with characters at the leaves. Each edge in the tree will correspond to a bit: a left edge corresponds to 0 and a right edge corresponds to 1. To get the encoding for a character, traverse the tree from the root to the leaf and concatenate all the corresponding bits.
Here’s a Huffman tree that contains all the characters in our string, go go gophers:

We have labeled each leaf with the frequency of that character. Internal nodes also have a frequency number that is the sum of all the frequencies of the children.
Here’s a table that shows the binary code for each character, according to this tree:
| Character | Binary code |
|---|---|
| 101 |
e | 1100 |
g | 00 |
h | 1101 |
o | 01 |
p | 1110 |
r | 1111 |
s | 100 |
Remember, you get the encoding by traversing the path from the root to the character, using a 0 for every left edge and a 1 for every right edge.
The Huffman tree ensures that characters that are more frequent in the input receive shorter encodings, and characters that are less frequent receive longer encodings. Our goal is to construct the Huffman tree, write the coding table, and write the compressed file using these shorter encodings.
Getting Started
To get started, obtain the release code by cloning your assignment repository from GitHub:
$ git clone git@github.coecis.cornell.edu:cs3410-2024fa/<NETID>_huffman.git
Replace <NETID> with your NetID. The characters in your NetID should all be in lower cases.
Assignment Outline
- Task 0: You will complete Task 0 in lab. You will implement a priority queue in
C as well as the
calc_frequenciesfunction inhuffman.c. - Task 1: You will implement the algorithm to create a Huffman tree.
- Task 2: You will implement the functions
write_coding_tableandwrite_compressedto write the coding table and compressed bytes to distinct files.
Implementation
(Lab) Task 0: Implementing a priority queue and frequency counter
Before starting, make sure you’ve cloned the release code by following the instructions in Getting Started.
Step 1: Implement a priority queue
The code for this portion is located in priority_queue.c, which is provided to
you in the release code. In this step, you’ll build a priority queue that accepts a “generic” data type.
This is accomplished by storing a pointer to an arbitrary piece of memory that
can store anything by using void*. We’ve provided a header
file that defines the PQNode type as well as the function declarations
for the functions you are required to implement.
Your implementation will go in priority_queue.c. We’ve provided a basic
test suite in test_priority_queue.c. You will implement the following
functions:
PQNode *pq_enqueue(PQNode **a_head, void *a_value, int (*cmp_fn)(const void *, const void *)): Add a new node with valuea_valueto a priority queue, using functioncmp_fn(...)to determine the ordering of the priority queue.PQNode *pq_dequeue(PQNode **a_head): Detach and return the head. Note, the caller is responsible for freeing the detached node, and any memory it refers to. Do not callfree.void destroy_list(PQNode **a_head, void (*destroy_fn)(void *)): Deallocates the priority queue. This should call thedetroy_fnfunction on every data element, and it shouldfreethe list nodes.PQNode *stack_push(PQNode **stack, void *a_value): Add a new node with valuea_valueto the front of the list.PQNode *stack_pop(PQNode **stack): Detach and return the head of the list. Note, this function is extremely similar topq_dequeue.
The last two functions are to enable us to use the same data structure as a stack,
when needed. You probably will not make use of this for your Huffman compression
system, but the decompression system needs a stack to work properly. If you can
implement pq_enqueue, and pq_dequeue, implementing stack_push and stack_pop
should be very easy.
We’ve provided a test file called test_priority_queue.c. Running rv make pqtest
from the command line will build an executable called test_priority_queue, which
you can then run by typing rv qemu test_priority_queue.
The tests use the header file cu_unit.h, which defines various macros that help
you write unit tests. In general, tests should be structured like so:
static int _test_name() {
cu_start();
//-------------------
// Setup code - build a list, declare a variable, call a function, etc.
cu_check(/*condition you want to check*/);
// ... add as many checks as you want
//-------------------
cu_end();
}
int main(int argc, char* argv[]) {
cu_start_tests(); // Indicate start of test suite
cu_run(_test_name); // Don't forget to run the test in `main`
cu_end_tests(); // Indicate end of the test suite
}
Upon running the test, you’ll see one of the two following messages:
Test passed: _test_name
which will be displayed in green, or:
Test failed: _test_name at line x
which will be printed in red, and give the line that failed. We’ve provided two
simple tests in the release code that check the behavior of your priority queue
and stack. You are encouraged to add more tests to verify the functionality
of your implementation. You will not be turning in test_priority_queue.c, however,
so this will not be graded.
Generic data types
You might notice some strange looking syntax in these function declarations.
This is to enable generic data types. The PQNode struct contains a void*, which
you can think of as a memory address to any type. This allows you to use the
same code for linked lists of any type.
You can assign a void* to an address of any type. This is why you can write
code like:
char* s = malloc(...);
even though malloc(...) returns a void*, not a char*. This is also similar
to the way functions such as qsort(...) allow you to sort arrays of any type.
Function addresses
Code that deals with generic data types often needs to pass functions as parameters.
To do this, you need to specify the address to a function as an argument. In other
words, you are declaring the parameter of the function (in this case cmp_fn) as
the address to a function that takes in some parameter(s) of specified types and
returns a value of a specified type. For the compare function, you’ll always
return an integer, and the arguments to the compare function can be anything,
depending on the underlying data in the nodes of the priority queue.
Let’s look at an example:
void _print_square(int n) {
printf("%d squared is %d\n", n, n * n);
}
void _print_cube(int n) {
printf("%d cubed is %d\n", n, n * n * n);
}
void _call_print_fn(int n, void(*print_fn)(int)) {
print_fn(n);
}
int main(int argc, char* argv[]) {
_call_print_fn(4, _print_square); // Prints 16
_call_print_fn(4, _print_cube); // Prints 64
}
In the above code, the type of parameter print_fn is void(*)(int). In other
words, print_fn is the address to a function taking an int and returning void.
Generalizing this to our priority queue, notice that the type of parameter cmp_fn
is int(*)(const void*, const void*). This is the address to a function taking
two addresses to memory locations of any type and returning an int.
Similarly, destroy_list also takes a function address. This is because beyond
freeing the node itself, you also need to potentially free whatever the node stores
(e.g., if you have a priority queue of dynamically allocated strings).
Implementing pq_enqueue
You might recall from CS 2110 that priority queues can be implemented with binary heaps. In our implementation, however, we will be implementing our priority queue as a linked list that we will keep sorted by priority. This means that inserting a node will be an O(n) time operation, and removing from the priority queue will be a constant time operation. This is fine for our purposes.
In pq_enqueue, *a_head refers to the head of the linked list. If
*a_head is NULL, then the list is empty. a_value is the address of whatever
value is associated with this node.
Allocate a new PQNode and insert it into the list in sorted order, according to the cmp_fn function.
That is, everything before the new PQNode should be less than the new one, and everything to the right should be bigger than (or equal to) the new one.
*a_head should be updated if the new node becomes the first item in the list.
The function should return the address of the new node.
This function should call malloc exactly once. You should not call
free in this function.
We recommend you test your implementation for your priority queue as you go in
test_priority_queue.c. You should also test your implementation for types other
than integers, including dynamically allocated types such as strings. You will need to
write your own comparison function to do this, and potentially your own print function if you
want to be able to print your list.
Implementing pq_dequeue
Like the previous function, *a_head refers to the head (first node) of a valid
linked list. If the list is empty, return NULL (since there is nothing to dequeue).
Upon return, *a_head must be a valid linked list (although possibly empty). For
our purposes, NULL is a valid linked list of size 0. Thus, *a_head will be
set to NULL if the list is empty, and upon removing the last node, you should set
*a_head to NULL.
You must also set the next field of the removed node to NULL. The caller
is responsible for freeing the detached node, and any memory it refers to.
For this reason, this function should not call free, directly or indirectly.
Again, you should test this by adding more statements to test_priority_queue.c
and printing the list to observe the behavior of your function.
Implementing destroy_list
This function should completely destroy the linked list referred to by *a_head,
freeing any memory that was allocated for it. destroy_fn(...) is a function that
deallocates *a_value as needed (if for example, the nodes of the priority
queue had values that were themselves dynamically allocated). This function should
set the head to NULL in the caller’s stack frame (i.e. *a_head = NULL).
This is a good point to check to make sure that your code does not leak memory.
Suppose you have the following code in test_priority_queue.c:
#include "priority_queue.h"
#include "cu_unit.h"
int _cmp_int(const void *a, const void *b) {...}
void _print_int(void *a_n) {...}
int _test_destroy() {
cu_start();
// ------------------
PQNode* head = NULL;
int n1 = 5, n2 = 7, n3 = 6;
pq_enqueue(&head, &n1, _cmp_int);
pq_enqueue(&head, &n2, _cmp_int);
pq_enqueue(&head, &n3, _cmp_int);
destroy_list(&head, NULL);
cu_check(head == NULL);
//--------------------
cu_end();
}
int main(int argc, char* argv[]) {
cu_start_tests();
cu_run(_test_destroy);
cu_end_tests();
return 0;
}
This code should contain no memory leaks,
i.e., it should eventually free everything that it mallocs.
You will likely want to use the sanitizers to check for memory bugs.
Running rv make pqtest also enables the sanitizers so you don’t have to write out
the command-line flags yourself.
Implementing stack_push and stack_pop
In stack_push, *stack stores the address of the first node in the linked list. a_value stores
the address of the generic type. The newly allocated node should become the first node
of the list, and *stack should be updated. The function returns the address
of the new node.
In this function, you will call malloc exactly once, and you will
not call free. This function is extremely similar to pq_enqueue, except you
don’t need to think about where in the list the node should go.
It always goes in the front of the list.
For stack_pop, you should simply detach and return the node from the head
of the linked list. Note that this is incredibly similar to the specification for
pq_dequeue.
Again, make sure you thoroughly test this code, as it will be used extensively in Task 1 and Task 2. If you are confident your code is correct, now would be a good time to commit and push your work to GitHub.
Step 2: Implementing calc_frequencies
The code for this task is located in huffman.c. You will be implementing the
following function:
calc_frequencies(Frequencies freqs, const char* path, const char** a_error): Open a file atpathand either store the character frequencies infreqor set*a_errortostrerror(errno).
Before getting started, we recommend you take a look at the type definitions and function
specification located in huffman.h. In particular, pay careful attention
to these two lines:
typedef unsigned char uchar;
typedef uint64_t Frequencies[256];
The first line tell us that uchar is simply an alias for an unsigned char. Similarly,
the second line tells us that Frequencies is an alias for an array of 256 unsigned
integer values.
For the function calc_frequencies, the caller is responsible for initializing
freqs[ch] to 0 for all ch from 0 through 255. The function should behave as follows:
- If the file is opened correctly, then set
freqs[ch]to n, where n is the number of occurrences of the characterchin the file atpath. Then, returntrue. Do not modifya_error. - If the file could not be opened (i.e.,
fopenreturnedNULL), set*a_errortostrerror(errno)and returnfalse. Do not modifyfreqs.
You only need to check for errors related to failure to open the file. This
function should not print anything, nor should you call malloc or free.
You do not need them.
This function will need to use file input/output functions from the stdio.h header.
In particular, use the documentation for fopen, fgetc, and fclose.
Working with files in C can be confusing at first. Let’s look at some of the
basic syntax:
#include <stdio.h>
#include <stdlib.h>
void print_first_character(char const* path) {
FILE* stream = fopen(path, "r"); // this opens the file in reading mode
char ch = fgetc(stream); // read one character from the file, starting from the beginning
fputc(ch, stdout); // write that character to stdout
fclose(stream); // always call fclose() if you call fopen()
}
int main(int arc, char* argv[]) {
print_first_character("animal.txt");
return 0;
}
In the fopen function, the second argument indicates the mode the file should
be opened in. "r" is for reading, "w" is for writing, and "a" is for appending.
If you wanted to write a function to print out every character in a file (and
not just the first), you’d write something like this:
void cat(char const* path) {
FILE* stream = fopen(path, "r");
for (char ch = fgetc(stream); !feof(stream); ch = fgetc(stream)) {
fputc(ch, stdout);
}
fclose(stream);
}
Be sure to use the stdio.h documentation to find the I/O functions you need.
Again, we recommend testing your code for calc_frequencies before moving on.
Create a file called test_frequencies.c, and an example file such as animals.txt.
Try calling your function and seeing if it correctly obtains the frequencies of
each character in the text file using cu_unit.
That’s all for Task 0 and the lab! Don’t forget to commit and push your code to GitHub.
Task 1: Building a Huffman Tree
In lab we created a priority queue that accepts a “generic” data type. We will use the priority queue in this task to build our Huffman tree.
If you missed lab or you don’t have a working priority queue or calc_frequencies function, go back and finish that first. Your code for this task will rely on the previous task.
The implementation for the Huffman tree will be contained in huffman.c. Look
carefully first at huffman.h to ensure you understand the functions you are
required to implement. In this task you will be implementing two functions:
TreeNode* make_huffman_tree(Frequencies freq): Given an arrayfreqwhich contains the frequency of each character, create a Huffman tree and return the root.void destroy_huffman_tree(TreeNode** a_root): Given the address of the root of a Huffman tree created bymake_huffman_tree(...), deallocate and destroy the tree.
Recall that freq is an array with 256 values. Each
index of the array is an ASCII character (recall that chars are just unsigned
bytes in C). The value of freq[c] is the frequency of character c in the
input file.
Also important in the header file is the definition of the TreeNode struct.
A Huffman tree node contains the character, the frequency of the character in the input, and
two child nodes. Huffman’s algorithm assumes that we’re building a single tree
from a set (or forest) of trees. Initially, all the trees have a single node
containing a character and the character’s weight. Iteratively, a new tree is
formed by picking two trees and making a new tree whose child nodes are the
roots of the two trees. The weight of the new tree is the sum of the weights of
the two sub-trees. This decreases the number of trees by one in each iteration.
The process iterates until there is only one tree left. The algorithm is as
follows:
- Begin with a forest of trees. All trees have just one node, with the weight of the tree equal to the weight of the character in the node. Characters that occur most frequently have the highest weights. Characters that occur least frequently have the smallest weights. These nodes will be the leaves of the Huffman tree that you will be building.
- Repeat this step until there is only one tree: Choose two trees with the
smallest weights; call these trees
T1andT2. Create a new tree whose root has a weight equal to the sum of the weightsT1 + T2and whose left sub-tree isT1and whose right sub-tree isT2. - The single tree left after the previous step is an optimal encoding tree.
To implement this strategy, use your priority queue to store your tree nodes. You want all the nodes to be ordered by their weights, so you can easily find the two trees with the smallest weights (at the front of the queue). You will need to write your own comparison function to implement this policy. To break ties when two tree-nodes have the same frequency, you can order them lexicographically by the ASCII value of the character.
We will not pay particular attention to the tie-breaking between a node and a non-leaf node, since those nodes are supposed to not hold a value in theory. Adding a tie-breaking here would make your implementation unnecessarily more complex. While there is only a single theoretically correct Huffman tree, this implies that the tree we build here can take on multiple forms. That’s fine; we will not grade based on the exact structure of your Huffman tree, but the properties delineated below.
When you test your code, you should make sure that calling destroy_huffman_tree(TreeNode** a_root)
ensures that your code has no memory leaks.
For testing, there are a few properties of Huffman trees we would like to verify:
- The weight of an internal node is equal to the sum of the weights of its children.
- The sum of the weights of the leaf nodes is equal to the number of characters in the uncompressed text.
- If the number of distinct leaf nodes is n, then the number of total nodes in the Huffman tree is 2n−1.
The last property follows from the fact that if you start with n leaf nodes, you need n−1 internal nodes to connect them.
We’ve provided you with a file test_huffman.c, which defines functions that
verify the aforementioned properties using cu_unit.h. We’ve provided three
test functions: one for each file given to you in the tests directory. You
are encouraged to add more thorough tests yourself; however, you do not need to turn
in test_huffman.c. Once you are confident your implementation is correct, move on to the next task.
To compile and run this program, you’ll run:
$ rv make hufftest
$ rv qemu test_huffman
Task 2: Writing the compressed file and coding table
Now we have all of the pieces we need to write the compressed file and
the coding table. For this task, you must implement two functions, found in huffman.c:
void write_coding_table(TreeNode* root, BitWriter* a_writer): Write the code table toa_writer->file. This function writes to a file calledcoding_table.bits.void write_compressed(TreeNode* root, BitWriter* a_writer): Write the encoded data toa_writer->file. This function writes to a file calledcompressed.bits
The above functions make use of the BitWriter struct, which is defined in
bit_tools.h. The BitWriter allows us to write data to a file in increments
of bits instead of bytes.
(Normal file writing APIs, including C’s standard stdio.h, only support writing entire bytes at a time.)
You are not responsible for fully
understanding the inner workings of BitWriter, but you do need to know how
to use it to write data to the file.
The BitWriter struct contains a file that
is already opened in "w" mode. To write bits to the file, you must call the
function write_bits(BitWriter* a_writer, uint8_t bits, uint8_t num_bits_to_write).
It takes three parameters:
a_writer: The address of aBitWriterthat contains a file which is open for writingbits: The bits you want to write, stored in auint8_tnum_bits_to_write: The number of bits you want to write, which must be between 0 and 8 inclusive
For both the compressed file and the coding table, you should only need to write
bits to the file in 1-bit and 8-bit increments. The following program may help in
understanding the behavior of the BitWriter more clearly:
int main(int argc, char* argv[]) {
BitWriter writer = open_bit_writer("new_file.bits");
write_bits(&writer, 0x05, 3); // 0x05 ↔ 00000101₂ ⋯ writes just 101₂
write_bits(&writer, 0xf3, 3); // 0xf3 ↔ 11110011₂ ⋯ writes just 011₂
write_bits(&writer, 0x01, 2); // 0x01 ↔ 00000001₂ ⋯ writes just 01₂
write_bits(&writer, 0x20, 6); // 0x20 ↔ 00100000₂ ⋯ writes just 100000₂
write_bits(&writer, 0x13, 5); // 0x13 ↔ 00010011₂ ⋯ writes just 10011₂
write_bits(&writer, 0x05, 5); // 0x05 ↔ 00000101₂ ⋯ writes just 00101₂
close_bit_writer(&writer);
return 0;
}
After running this code, you can inspect the new_file.bits file using the
following command:
$ xxd -b -g 1 new_file.bits
The xxd tool prints out files in binary, hex, and ASCII formats so you can see exactly what you have written.
Implementing write_coding_table
The coding table is a file that encodes the structure of your Huffman tree in a
text file. It is an important utility for the decompression algorithm, as it
allows you to recover the structure of the Huffman tree without needing the original
uncompressed text. In this step, we will write the encoded Huffman tree to a file
called coding_table.bits.
To write the coding table, you do a post-order traversal of your Huffman tree.
- Traverse the left subtree of the root (i.e., encode it to the file).
- Traverse the right subtree of the root (i.e., encode it to the file).
- Visit the root.
Every time you “visit” a node (including the root of a subtree):
- If it is a leaf (i.e., character), you write one bit:
1. Then, you write the entire character (8 bits). Example: If the character isA, you will write0b101000001. The1is to signify that it is a leaf. The0b01000001is to specify the character itself. - If it is a non-leaf (i.e., an internal node), you write one bit:
0.
To write out the bits for a character, you can pass a char value directly to write_bits.
For example, use write_bits(my_writer, 'A', 8) to write out the binary encoding of the character A.
Your code will write the bits for the coding table using BitWriter. To make the coding table more explicit, consider the following Huffman tree for go go gophers again:

If we provide this tree as an input to write_coding_table, the coding table representation should look like 1g1o01s1 01e1h01p1r00000, and in complete binary (as formatted by xxd), it would be represented as:
00000000: 10110011 11011011 11010111 00111001 00000010 11001011
00000006: 01101000 01011100 00101110 01000000
Notice that the first bit is a 1, indicating a leaf, followed by the byte
01100111, which represents the character g in ASCII. Write the bits of the
coding table to the file only. Do not write anything before or after the
encoding of the Huffman tree.
Before we move on, here’s another reminder that the Huffman tree you build in make_huffman_tree can take on various forms depending on how you tiebreak the non-leaf nodes; there is no single “correct” Huffman tree for the purpose of this assignment. This means your binary representation generated by the compression driver below for go go gophers might not match the example above; in fact, in our implementation we got:
00000000: 10111001 11011001 01101101 00000101 10011101 01101111 ..m..o
00000006: 10111000 01011100 10010010 00000000 .\..
So even if your coding table for the gophers example might not match our examples in this instruction, there is no need to fret. Just make sure to verify that your coding table matches your Huffman tree and run some tests.
You can verify the functionality of your write_coding_table by running the compression driver:
$ rv make
$ rv qemu compress tests/ex.txt
$ xxd -b -g 1 coding_table.bits
Running the compress binary will produce two files: coding_table.bits and
compressed.bits. You can inspect each of these files to verify the correctness
of the write_coding_table and write_compressed functions, respectively.
Implementing write_compressed
In this step, we will write the compressed data to compressed.bits. The argument
a_writer to the function points to a BitWriter that has compressed.bits open
for writing. To write the compressed data, you will need to traverse your Huffman tree to
recover the encodings, and then use the encodings to write the compressed data.
How you accomplish this is largely up to you—there are many valid approaches
here. Just make sure that there are no memory leaks and that your compressed
data file actually represents the Huffman encodings. Again, write the bits of
the compressed data only—do not write any bits before or after the compressed
bits.
When you go to inspect the file, you may notice that there are an additional
four bytes written to compressed.bits before the compressed data itself. These
bytes represent the size of the original uncompressed text in bytes. Integers
are typically four bytes, so we use four bytes to write this information to the
file. This is written for you by the compression driver (do not write this
yourself). The reason it’s there is for decompression—the decompression
program needs to know how big the original text file was to recover the
uncompressed text.
Using the go go gophers example, the compressed data
should look something like (where there are four additional bytes at the beginning):
00000000: 00001101 00000000 00000000 00000000 01101110 11011101 ....n.
00000006: 10110000 11001011 01000000 ..@
Notice that if you use the command ls -l, you can see the sizes of your files
in the directory in bytes. The original file was 13 bytes but the compressed
file is 9 bytes—our compression was successful!
Running and Testing
To make it easier to compile and run your code, we’ve provided a Makefile. To
build your program, simply type rv make. rv make will build two executables: a
compression program and a decompression program. To run the compression
program, type:
rv qemu compress <filename>
This will produce two output files: compressed.bits and coding_table.bits. If
you run the compression program on another input file, the two output files will
be overwritten with the new results.
To run the decompression program, type:
rv qemu decompress compressed.bits coding_table.bits <uncompressed_filename>
This produces a file called <uncompressed_filename>. To see if your compression was
successful, you can try comparing the result of the decompression to the
original unencoded file by running:
diff <original_file> <uncompressed_file>
For example, if you were trying this on the cornell.txt file in the tests
directory, you’d run:
$ rv qemu compress tests/cornell.txt
$ rv qemu decompress compressed.bits coding_table.bits uncompressed_cornell.txt
$ diff tests/cornell.txt uncompressed_cornell.txt
If you see nothing when running this, that means the files are identical and decompressing your compressed file was successful. Good work!
Note that the decompression tool is based on your implementation of the coding table and the Huffman tree. In other words, you might be able to decompress your file correctly, but that does not mean your Huffman tree is correct.
Round-trip compression and decompression is necessary for the correctness
of the entire system, but not sufficient, to
guarantee that all of the functions from Task 1 and Task 2 are correct. You are
strongly encouraged to use cu_unit.h (described in Task 0) to more
thoroughly test your code for Task 0 and Task 1. You can add tests directly to test_priority_queue.c
and test_huffman.c. You are not required to submit these files, but we strongly
encourage you to test each task separately as that is how your code will be graded.
To build the test executables, you can run:
$ rv make pqtest
$ rv make hufftest
which will generate test_priority_queue and test_huffman, respectively.
Submission
Submit huffman.c and priority_queue.c to Gradescope. Upon
submission, we will provide a sanity check to ensure your code compiles and
passes the public test cases. The public test cases will only test for
round-trip compression and decompression, and not intermediate functions.
Rubric
- Task 0: 30 points
- Task 1: 30 points
- Task 2: 40 points
Code that contains memory leaks as reported by the sanitizers will be subject to a deduction of 50% of the total points for the assignment.
Generating Circuits
Instructions:
Remember, all assignments in CS 3410 are individual.
You must submit work that is 100% your own.
Remember to ask for help from the CS 3410 staff in office hours or on Ed!
If you discuss the assignment with anyone else, be careful not to share your actual work, and include an acknowledgment of the discussion in a collaboration.txt file along with your submission.
The assignment is due via Gradescope at 11:59pm on the due date indicated on the schedule.
Submission Requirements
You will submit your completed solution to this assignment on Gradescope. You must submit:
quine_mccluskey.c, which will contain your implementation in Task 1 and Task 2.tests.txt, containing your five new test inputs from Task 3.
Restrictions
- Do not modify any source files other than
quine_mccluskey.c.
Overview
You will implement a program that generates a logic circuit for a given truth table. This assignment covers the fundamentals of Boolean algebra and logic circuits.
Background
In class, we practiced a “recipe” for mechanically building a circuit to implement any Boolean function using its minterms. While this recipe works, it can yield pretty big and complicated circuits. There is an entire universe of techniques that attempt to design small, efficient circuits for a given truth table instead.
Consider the Boolean expression abc+ab¯c. (If you need a reminder about logic notation, see the lecture notes.) Notice that the c term doesn’t matter here: for all values of a and b, the value of the expression is the same regardless of whether c is true or false. So this expression is equivalent to ab. If you imagine the circuit to implement this expression, it’s a lot simpler: it just uses one AND gate, instead of the original’s four ANDs and an OR.
Compact Notation for Simple Boolean Expressions
We will need a simple way to represent the Boolean expressions we’ll be dealing with, which are generally “ands” of possibly-negated variables. The idea is to take conjunctions like a¯bc and to represent them with symbols, where the nth symbol corresponds to the nth input variable. The symbols are:
- 0: Negated variable, like ¯a in a real Boolean expression.
- 1: Non-negated variable, like a.
- x: Don’t care, i.e., like not including the variable in the “and” at all.
For example, if we have three variables named a, b, and c:
- The compact notation
110denotes the expression ab¯c. 01xdenotes ¯ab.1x1denotes ac.
Quine-McCluskey Algorithm
The Quine-McCluskey algorithm, a.k.a. the method of prime implicants, is a technique for finding smaller, more efficient Boolean expressions. Let’s define some terms:
- An implicant is a Boolean expression that “covers” several minterms:
for example,
1x1covers both111and101. In other words,1x1in our compact notation is equivalent to “111or101,” so it is an implicant that covers those minterms. - A prime implicant is an implicant that can’t be covered by some other, more general implicant.
The Quine-McCluskey algorithm works by finding these prime implicants and then using them to make the final Boolean expression.
The algorithm has two steps:
- Generate a set of all prime implicants by merging minterms.
- Select certain prime implicants to simplify the expression.
The first step works by starting with a set of minterms and
merging them together to produce implicants that cover them.
Two minterms can be merged if they differ in at most one position;
merging them produces an implicant where that one position becomes x (don’t care).
For example, the minterms 100 and 110 can be merged into 1x0
(check that you agree that the corresponding Boolean expressions are equivalent!).
But 100 and 111 cannot be merged into 1xx (because 1xx would also encompass the minterms 110 and 101, which are not in our original pair).
The first step works by checking every pair of minterms to see if they can be merged. Then, it repeats: it checks whether any pair of those implicants can be merged using the same rule. The step finishes when it can’t find any more more mergeable pairs. This step is Task 1 on this assignment.
The second step selects a smaller set of these prime implicants that covers the original set of minterms. We will describe the algorithm in Task 2.
Finally, we combine the reduced set of prime implicants with “or” to produce our final sum-of-products Boolean expression.
Program Overview
You will write a program that produces a simplified Boolean expression for a given truth table. Let’s use this truth table as an example:
| a | b | c | out |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Our program will work by taking the truth table’s minterms as input,
using our compact notation.
The minterms in this example are 001, 011, and 111.
The user would input a file with one minterm on each line:
001
011
111
If we wrote out the sum-of-products expression in standard notation, it would be ¯a¯bc+¯abc+abc.
When we run our program, however, it will produce the prime implicants 0x1 and 111.
These represent the simpler, equivalent Boolean expression ¯ac+abc.
The program will write the selected prime implicants in a file called output.txt.
Implementation
Task 0: Lab Section
In this lab, you will gain practice working with Boolean circuits (Section 1). You will also try a manual method for Boolean simplification (Section 2).
Section 1: Play Nandgame
This section of the lab uses Nandgame, a browser-based game about digital logic, to get experience with constructing circuits.
XOR. Open Nandgame and skip the first 4 levels (although feel free to come back later and try them yourself). We’ll start with the XOR circuit. Nandgame gives you a truth table for XOR, toolbox with some logic gates, and a canvas. Drag and drop components from the toolbox to the canvas, and connect inputs and outputs by clicking on the triangular inputs and clicking on the circular output of another component. Spend a few minutes trying to create your solution.
If you give up after trying for a while, here’s one possible solution:
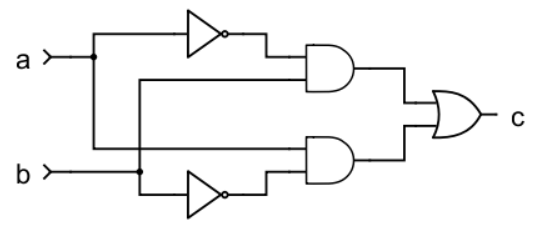
1-bit adder. Next, implement a 1-bit adder. Read more about half adders and full adders in the lecture notes. Try these levels in Nandgame.
Try it for at least a while before looking at one possible solution below:
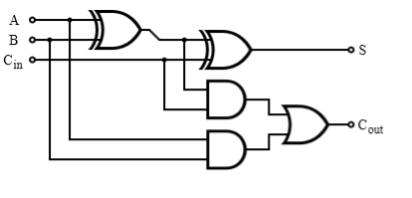
Multi-bit adder. You can create an n-bit adder by cascading n full adders. Create the 2-bit adder in Nandgame by reusing the 1-bit adder provided. If you ever need help, feel free to ask a TA.
Ponder the fact that your strategy would be straightforward to extend to an n-bit adder for any n!
Checkoff #1: Show your two-bit adder to your TA.
Section 2: Karnaugh Maps
Karnaugh maps (a.k.a. K-maps) are a popular method for manually minimizing Boolean expressions. It has some similarities to the Quine-McCluskey algorithm you’ll implement, but it’s meant for human use instead of algorithmic implementation.
Introduction to Karnaugh Maps
A K-map is a 2-dimensional grid that represents a Boolean function. The rows and columns represent the inputs; the value in the cell (1 or 0) represents the output. This layout makes it possible to find groups of 1 cells, which can then be transformed into simplified expressions.
To construct a K-map, divide the input variables of the truth table into two groups.
One group is assigned to the rows in the grid, the other to the columns, and for each group,
we will have one row/column for each possible combination of input values. Each cell in the
grid contains the output value (0 or 1) for the truth table row that corresponds to those
inputs.
You may find it helpful to think of the inputs as a binary number where its
corresponding cell can be found by finding the intersection of its x and y axis. The
image below shows three blank K-maps, with the small boxes containing the decimal values
of the row/column binary numbers.
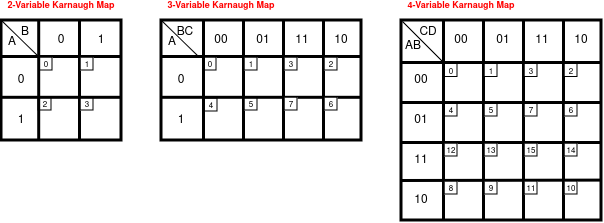
The order in which the truth table elements are mapped may look surprising:
the axes don’t work by counting up by 1 at each step.
Instead, we
choose an ordering that ensures only one variable
changes at a time as you move down a column or row.
So instead of having 10 next to 01, which switches both bits, we have 11 next to 01 instead, because only one bit switches.
This strategy is called a Gray code ordering.
After you fill out all the cells with the circuit’s output value, the next step is to find groupings of 1 cells. (These 1 cells correspond to the minterms.) Groupings must follow these rules:
- All 1s must be a part of a group.
- No 0s can be a part of a group.
- The grouping size must be a power of 2 (1, 2, 4, 8, etc.).
- Groups are always rectangular (no diagonals).
- Overlapping groups are allowed.
- Wrapping around the map is allowed.
- To find optimal groupings, you would also make the groups as large as possible and have as few as possible.
Here’s an example K-map for a 4-input truth table:
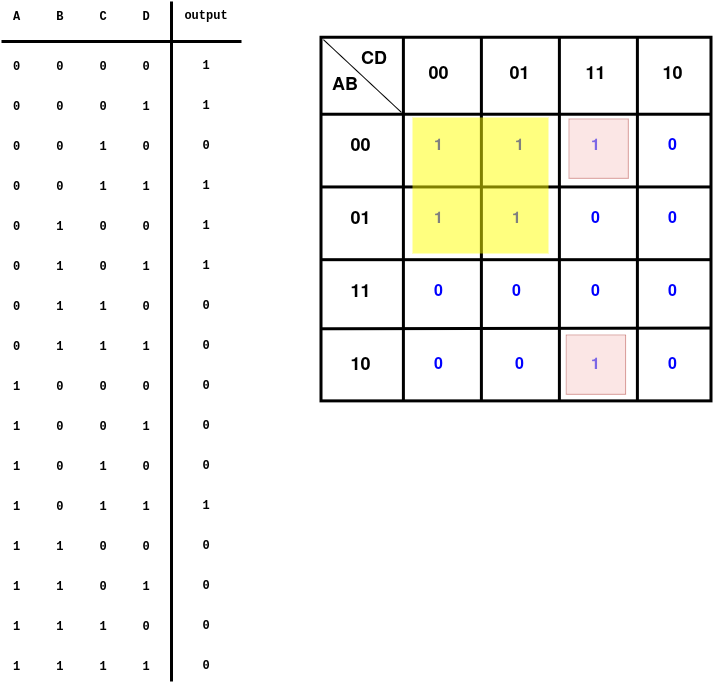
There are multiple valid groupings. We have shown a solution with two groupings, which is the smallest possible number for this truth table.
Each grouping represents an implicant (a Boolean expression that covers one or more minterms). To find the Boolean expression for an implicant, observe which variables change in a certain grouping and which variables remain constant. Include only the variables that remain constant in the expression.
In our example, here are the expressions for our groupings:
-
Yellow group:
Implicant in compact notation:0x0x
In standard notation: ¯A¯C -
Pink group:
Implicant in compact notation:x011
In standard notation: ¯BCD
Finally, to create the final Boolean expression, combine the expressions with an OR. The final expression here is:
¯A¯C+¯BCD
K-maps are amazing at quickly simplifying smaller boolean expressions and are great for humans to visualize. However, this approach does not scale well. Because K-maps are reliant on human pattern recognition and are done by hand, they are not often used for anything beyond four input variables.
Try Out Karnaugh Maps
Let’s try out the K-map technique! We’ll use the approach for the logic underlying a 7-segment display, like on a microwave:
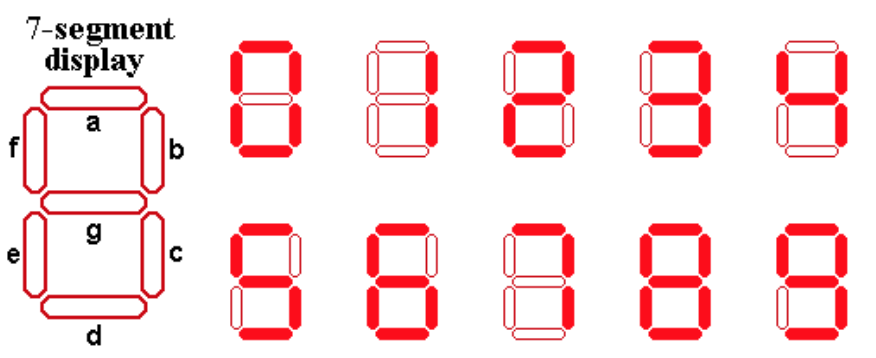
The idea in this lab exercise is to build the logic that takes in a 4-bit number representing a value from 0 to 9 and lights up the appropriate segments of the display.
For example, when the input is 0111, we want only segments a, b, and c to light up so the display looks like the number 7.
You can think of each segment having its own truth table that describes, for a given 4 input bits, whether it should turn on.
Step 1: Truth Table. Create a truth table for the top right section (segment b) of a 7-segment display. You only need to handle inputs in the range 0–9; other inputs are undefined. Write this truth table on paper. Here are the first few rows (with the output filled in only for the first one) to get you started:
| Input (decimal) | Bit 3 | Bit 2 | Bit 1 | Bit 0 | Segment b Result |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | |
| 2 | 0 | 0 | 1 | 0 |
We’ve augmented this truth table with an extra (leftmost) column where you can write the decimal value of the 4-bit number. The first row’s output is 1 because, to make the shape of the number 0, the top-right segment is turned on.
Step 2: Minimize Using a Karnaugh Map. Use the K-map technique to minimize the circuit for the “top right” segment. Remember, you will need to:
- Draw an empty 4-input K-map.
- Fill in the cells with the outputs from your truth table. For the cells where the output is undefined, because the input number is greater than 9, fill in 1s.
- Try to find the fewest, largest groupings of 1s in your K-map.
- Write the corresponding implicants.
- Join the implicants with “or” to write the final Boolean expression in standard notation.
Try to convince yourself that your new, simplified expression is a correct description of segment b’s behavior.
Checkoff #2: Show your Karnaugh map and your minimized Boolean expression to your TA.
Task 1: Finding All Prime Implicants
In this task, you will implement the first part of the Quine-McCluskey
algorithm where you must find all prime implicants for a given set of minterms.
Your implementation will go in quine_mccluskey.c.
You will implement these five functions:
checkDashesAlign: A helper function formergeMinterms.checkMintermDifference: A helper function formergeMinterms.mergeMinterms: A helper function forgetPrimeImplicants.addMinterm: A general helper function.getPrimeImplicants. The main function for this task.
Read quine_mccluskey.h for the specifications for all of these functions.
At a high level,
the idea is that we can merge two terms of the same length if both of these conditions are met:
- Their “don’t-cares” (
x) appear in the same positions. (There is no position where one term has anxand the other has a0or1.) - They differ in at most a single position.
The helper functions checkDashesAlign and checkMintermDifference check these conditions.
We have designed this assignment so it does not require dynamic memory allocation (malloc).
But it is not forbidden.
Handling the String Inputs
Here’s are some hints for how to use the arrays of strings that get passed to these functions. Remember that C strings are null-terminated arrays of characters, and some functions receive arrays of these arrays as arguments.
For example, one of the parameters to getPrimeImplicants is the minterms:
char minterms[MAX_TERMS][MAX_LENGTH].
You can think of this as an array of strings, or as a 2D array of characters.
There can be at most MAX_TERMS minterms, and each one can have at most MAX_LENGTH characters.
But in general, there will be fewer terms than the maximum, and each term will have fewer characters than the maximum.
Because strings in C are null-terminated, remember that the last character is always '\0' (the null byte).
In an empty string, this is also the first character!
Our code uses empty strings for the “unused” terms.
So to iterate over all the (non-empty) minterms, you can iterate until you find a string whose first character is null, like this:
for (int i = 0; minterms[i][0] != '\0'; i++) {
/// ...
}
Then, if you want to iterate over all the characters in a given string, you can again iterate until you hit a null byte. For example, this prints out all the characters for all the minterms:
for (int i = 0; minterms[i][0] != '\0'; i++) {
for (int j = 0; minterms[i][j] != '\0'; j++) {
fputc(minterms[i][j], stdout);
}
fputc('\n', stdout);
}
Task 2: Selecting Prime Implicants
In this task, you will
select a reduced subset of prime implicants.
Your implementation will again go in
quine_mccluskey.c.
You will implement one function: findMinimizedPrimeImplicants.
As always, it is OK to implement your own helper functions if you want.
The idea with this step is that some prime implicants can be redundant, and it’s possible to select a subset that suffice to cover all the minterms. Here’s an example:
- Start with these minterms:
010,101,110,111 - Our approach in Task 1 would produce these prime implicants:
x10,1x1,11x - However, it suffices to keep only these selected prime implicants:
x10,1x1
This smaller set of selected prime implicants covers the full set of minterms.
Here is an algorithm to select a smaller set of prime implicants:
- Find all essential prime implicants. These are prime implicants that cover at least 1 minterm that is not covered by any other prime implicants. The specific algorithm to achieve this is described below.
- Check if the essential prime implicants covers every minterm. If so, we have found the minimal list of prime implicants.
- If the essential prime implicants do not cover every minterm, we must add some prime implicants to our finalized expression to cover every minterm. The specific algorithm to achieve this is described below.
Finding Essential Prime Implicants
To find all essential prime implicants, you will want to construct a 2D chart
comparing minterms and prime implicants. Set up this chart with the minterms on
the top and the prime implicants on the left. Fill in this chart, indicating
what minterms are covered for each prime implicant. For example, using the
previous example’s minterms 010, 101, 110, 111, and the prime implicants
x10, 1x1, 11x, we can create the following chart.
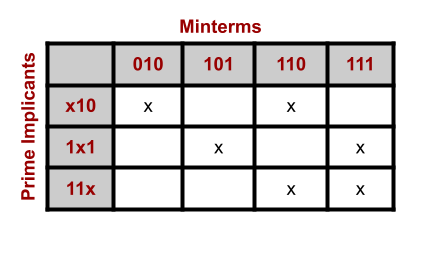
From here, we can easily identify essential prime implicants by looking for any
columns that contain only one X. In our example above, we see the minterms
010 and 101 fit this description, only being covered by the prime
implicants x10 and 1x1 respectively. Therefore, x10 and 1x1 are
essential prime implicants and must be included in the boolean expression.
In this specific case (although not in general), the essential prime implicants
also cover the remaining minterms of 110 and 111. Therefore, we can comfortably
drop the prime implicant 11x from our final set of prime implicants while
maintaining full coverage of our minterms.
We recommend that you declare a 2-dimensional array of bools to implement this chart.
You can declare it like this:
bool chart[MAX_TERMS][MAX_TERMS] = {false};
That initializes every entry in the 2D array to false.
Covering Remaining Minterms
If our list of essential prime implicants do not cover every minterm, we will use the following procedure to find remaining prime implicants:
- For every minterm:
- If it is not yet covered:
- Iterate over all inessential prime implicants to find one that covers the uncovered minterm, and add it to our set.
- When we do add a new prime implicant, mark all the minterms it covers as covered (so we don’t attempt to cover them again). (Remember that prime implicants might cover more than one minterm!)
- If it is not yet covered:
For example, suppose we have the minterms 1001, 1101, 1111, 0111, 0110
and the prime implicants 1x01, 11x1, x111, 011x. For the sake of brevity, you should find the eseential prime implicants to be 1x01 and 011x. However, these do not cover the minterm 1111.
- First, we try to cover
1111. By looking through all the inessential implicants (11x1andx111), we find that11x1suffices to cover this minterm.
So our final set of implicants is 1x01, 011x (the original essential prime implicant),
and 11x1.
Please also iterate over the minterms and prime implicants in the order the function receives them. This will make your solution match ours, which will make autograding go more smoothly.
Just for fun, if you want an extra challenge, you can try implementing Petrick’s method. Unlike our simpler strategy here, Petrick’s method finds minimized circuits. (Please do not submit this code if you try it!)
Task 3: Tests
Running and Testing
We have included a few example inputs in the tests/ directory.
Inputs are text files with one minterm per line, like this:
100
001
101
111
To run your implementation on one of these inputs, first compile it:
rv gcc -o quine_mccluskey quine_mccluskey.c
Then, run your program on an input file:
rv qemu quine_mccluskey tests/cout.txt
(Pick a filename and provide it as a command-line argument in place of tests/cout.txt.)
The program will write the selected minterms to output.txt.
Visualizing Your Circuits
Are you curious to see what the circuit schematics would look like for your simplified expressions? We have included a tool to draw these for you! This is completely optional.
The tool is implemented in Python, and it has some dependencies you need to install. A command like this might work:
python3 -m pip install -r requirements.txt
Then, if you already have some minimized implicants in a file output.txt, then you can run this to see a schematic:
python3 generate_circuit.py
Provided Tests
We’ve included some tests named mux.txt, cout.txt, input3.txt, input4.txt, and input5.txt. Use these to help debug your program as necessary.
Here are a descriptions of two of these tests:
-
The multiplexer (mux) selects one of two inputs based on a select input.
- Minterms:
010,101,110,111 - Prime Implicants:
x10,1x1,11x - Selected Prime Implicants:
x10,1x1
- Minterms:
-
The full adder has 3 inputs: A, B, and CarryIn. It has 2 outputs: Sum and CarryOut. Here is the logic for the CarryOut output:
- Minterms:
011,101,110,111 - Prime Implicants:
x11,1x1,11x - Selected Prime Implicants:
x11,1x1,11x
- Minterms:
Creating Your Own Tests
For the final part of this assignment, you will make five additional input tests that are different from the ones we supply. Make up some truth tables that compute interesting Boolean functions, and check that your implementation works correctly on them.
Turn in a file tests.txt that lists your five tests.
For each test, include in tests.txt:
- The list of minterms.
- A one-sentence description of what the circuit computes.
Your tests can do anything you like, as long as they do not match our tests. Be creative!
Submission
What to submit:
- A complete implementation in
quine_mccluskey.c. - 5 test expressions, in
tests.txt.
Rubric
- 80 points for
quine_mccluskey.c. - 20 points for the tests
CPU Simulation
Instructions:
Remember, all assignments in CS 3410 are individual.
You must submit work that is 100% your own.
Remember to ask for help from the CS 3410 staff in office hours or on Ed!
If you discuss the assignment with anyone else, be careful not to share your actual work, and include an acknowledgment of the discussion in a collaboration.txt file along with your submission.
The assignment is due via Gradescope at 11:59pm on the due date indicated on the schedule.
Submission Requirements
For this assignment, there are two files to submit:
logic.cwith the listed functions all implemented.tests.txtwith all of your test cases in the correct format.
Restrictions
- You may not use any additional include directives.
- Please only change
logic.c. Changes to other files will not be reflected in your submission.
Provided Files
The following files are provided in the release:
logic.c, which includes the five functions you will implement in this assignment.runner.c, which handles I/O and the structure of the simulator.hash_table.c, an implementation of a simple hash table.hash_table.h, which is the above’s associated header file.sol.h, which includes the signatures of the functions inlogic.candhash_table.c, as well as usefuldefinemacros and variable declarations.Makefile, which will appropriately compile and link the above to produce an executable,runner.check.s, a simple assembly program to be used as a sanity check.check.bin, the input to the program, which is the result of assemblingcheck.s.
The only file among these that you will modify is logic.c.
Submission
As always, you will find the starter in your personal repository on GitHub. You will submit your solution on Gradescope.
Overview
In this assignment, you will implement a subset of the RISC-V 64 instruction set. In order to gain a better understanding of control logic, processor architecture, and how assembly language functions, you will simulate the steps—Fetch, Decode, eXecute, Memory, Writeback—of a simple single-cycle processor. You can read more about these steps in the lecture notes.
The program takes assembled RISC-V machine code into standard input. We handle the I/O and break the instructions down into an array of uint32_t values, named instructions. instructions[0] has the 32-bit encoding for the first instruction, and generally, instructions[PC / 4] has the 32-bit encoding for the PC / 4 + 1st instruction (i.e., the instruction at address PC in the input file). The instruction encodings follow the standard that is specified in the RISC-V ISA manual.
After the instructions are fed into the program, while the program counter (divided by 4) is less than the static instruction count, it will continuously, in order, call the functions fetch(), decode(), execute(), memory(), and writeback().
Each of these 5 functions passes information to the next stage. fetch() will pass the current instruction to decode(), which will pass relevant information to execute(), which will pass other information to memory(), which will pass more information to writeback(), which will update the registers and the program counter. The relevant information is stored in a struct called info, which has 4 integers. It is up to you to decide exactly what information to store in the info struct, and not every stage will need all the bits.
The info struct is meant as a container for arbitrary bits.
There is no single correct way to use its fields to represent the relevant state.
You will use the info struct in entirely different ways for each of the four stage → stage communication steps.
The 32 general-purpose registers are simulated as an array of 32 uint64_ts. The starter code initializes all of these to 0.
Memory is simulated as a hash table, data, that maps from uint64_t to uint64_t. The keys are addresses, and the values are the data stored in memory. We suggest mapping an address to one byte of data, but an alternative such as mapping addresses to four or eight bytes is also acceptable.
An implementation of a hash table is provided in hash_table.c and hash_table.h. All key (address) → value (data) mappings are effectively initialized to 0, as the ht_get() function returns 0 when the key is not found.
Use the little-endian byte order for your simulated memory.
For example, when storing an 8-byte value to address a, store the least-significant byte at a and the most-significant byte at address a+7.
Assignment Outline
- Work out a high-level plan and implement
addiandandi, detailed in Task 0. - Implement the rest of the instruction subset, detailed in Task 1.
- Create a thorough test suite that you will submit, specified in Task 2.
Implementation
The release code is found on GitHub.
Task 0: Getting Started in Lab
Task 0.0: Design Plan
As stated in the overview, one of the goals of the assignment is to familiarize yourself with the important steps in a simple five-stage processor. The figure below may be used as reference.
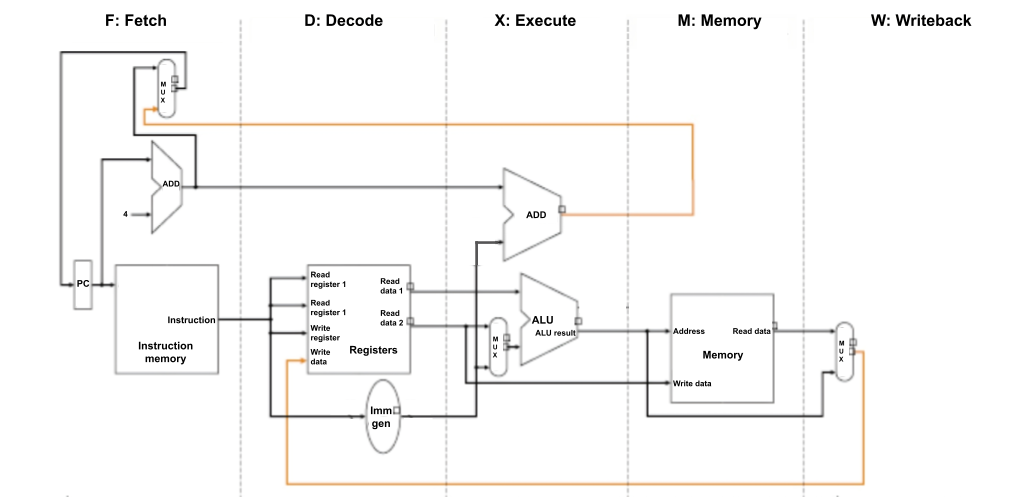
The five stages of the processor that you simulate are:
-
Fetch an instruction from main memory. The PC (Program Counter) holds the address of the instruction to fetch.
-
Decode the instruction into relevant parts that the processor understands, and read the requested register(s). Things to consider: What info is important to extract from an instruction? How should we generate the correct immediate value from the bits in the instruction? How do we single out bits that differentiate instructions—what makes
lwdifferent fromswor fromsb? -
Execute the instruction to determine its result value.
-
Access memory (here simulated as a hash table) to load/store data, if necessary. Things to consider: How should the stage differentiate bytes vs. words vs. double words? When should this stage sign-extend or zero-extend values when loading and storing?
-
Write back a new value for the PC, which should—except in the case of a branch—increment by 4 after every cycle, since each instruction is expressed with 4 bytes. Also, write back a newly computed value to the register file, if necessary. Things to consider: When should we write to the register file at all? What should we increment the PC by?
Create a high-level plan for what each function should do and what information it should pass to the next stage. For example, the Memory stage is the only one that accesses memory, and the Decode stage will be the only one that deals with bit-level slicing of the actual instruction word.
While it would certainly be possible to simulate everything in one function, implementations that are not faithful to the purpose of each stage will incur penalties.
Task 0.1: addi and andi
Now that you have a plan, let’s walk through two instructions.
-
addi rd, rs1, immis implemented as:
Registers[rd] = Registers[rs1] + Sign-extend(imm) -
andi rd, rs1, immis implemented as:
Registers[rd] = Registers[rs1] & Sign-extend(imm)
Consult the RISC-V reference card to see the encodings for these instructions.
Both addi and andi are I-type instructions, and thus have this encoding:
| 31 – 20 | 19 – 15 | 14 – 12 | 11 – 7 | 6 – 0 |
|---|---|---|---|---|
| imm[11:0] | rs1 | funct3 | rd | opcode |
The reference also tells us the values of the opcode and funct3 fields:
| Instruction | opcode | funct3 |
|---|---|---|
addi | 0010011 | 000 |
andi | 0010011 | 111 |
The fetch stage will get the instruction
at index PC / 4.
Then, for addi and andi instructions, the argument to the decode stage will be a uint32_t whose binary is of one of the two following forms:
0b[XXXXXXXXXXXX][XXXXX][000][XXXXX][0010011]
0b[XXXXXXXXXXXX][XXXXX][111][XXXXX][0010011]
Using bitwise operators, differentiate between the two functions and extract the relevant pieces of information to send to the execute stage.
Hint: Consider using one of the integers in info to communicate which instruction it is. We provide a mapping from instructions to integers via the #define macros in sol.h.
Now, in execute, we will use the operands to compute the result. Since neither addi nor andi should use the memory stage, think about what information the writeback stage will need, and send this to memory, which will be a no-op.
After using the memory stage to send the information from execute to writeback, consider how your writeback stage should update the state of the program to prepare it for the next instruction.
Trying It Out
To test your implementation, we can write a simple assembly program, prog.s, using addi and andi. It could look something like this:
addi ra,zero,0x155
andi sp,ra,0x1b9
In order to obtain the binary to be used as standard input, run either of the two following equivalent commands that assemble prog.s to machine code and copy its contents as raw binary to prog.bin:
- Option 1:
asbin prog.s - Option 2:
as prog.s -o tmp.o && objcopy tmp.o -O binary prog.bin && rm tmp.o
(Option 1 works because we have provided, in the CS 3410 container, a shorthand script asbin that just runs the commands in Option 2.)
Compile your simulator with make, producing an executable named runner.
Now you can run the program with prog.bin as standard input with:
qemu runner < prog.bin
Upon successful execution of runner, the values of the 32 general purpose registers will be printed in hexadecimal.
Testing Routine
To summarize, here are the commands to run if you want to execute your simulator on an assembly program:
$ rv make
$ rv asbin your_great_test_program.s
$ rv qemu runner < your_great_test_program.bin
As always, you can use the rv alias to run commands in the official CS 3410 container.
Task 1: Simulating a RISC-V CPU
Now that you have addi and andi working, implement the remainder of the RISC-V 64 subset listed in the table:
| Format | Instructions |
|---|---|
| R-type | ADD, SUB, AND, SLT, SLL, SRA |
| I-type | ADDI, ANDI, LD, LW, LB |
| S-type | SD, SW, SB |
| U-type | LUI |
| B-type | BEQ |
In the official RISC-V ISA manual, these instructions are part of the RV64I Base Integer Instruction Set, a superset of RV32I (Chapters 2 and 4). A table with the encodings is in Chapter 19. You can also use the shorter reference card, which only includes the RV32 instructions, or use the extended handout (recommended) for RV64 instructions.
For the purposes of testing, command line arguments of the form <register number>@<hexadecimal value> set the starting values of individual registers. For example, to set the initial value of register 5 to 0xbeefdeadbeef and the initial value of register 12 to 0xc, the command would be
qemu runner 5@0xbeefdeadbeef 12@0xc < prog.bin
In the release files, we provide a basic test, check.s, and the output of asbin check.s, check.bin. This is also the sanity check that the autograder will run upon submission.
Behavior of BEQ
The RISC-V assembler lets you write beq instructions in two different ways:
with labels or write immediate addresses.
Because of an assembler quirk, we recommend that you only use labels.
Here’s some more detail.
The assembler will convert an instruction of the form beq rs1, rs2, z where z is an immediate address into a sequence of two instructions:
bne followed by a jal. This behavior allows assembly programmers to use beq as a pseudoinstruction for jumps beyond what can be done in one actual machine beq instruction. (The addresses of the instructions are not known until linking, so the assembler does not know if the immediate in the beq instruction is within range).
We do not expect you to implement bne or jal in this assignment, so we need to write assembly programs to avoid this “convenient” behavior.
Instead, to ensure that the assembler encodes an actual beq instruction, we can use labels with optional offsets.
Write your beq instructions in one of these forms:
beq rs1, rs2, L1whereL1is a label at the instruction you want to jump to.beq rs1, rs2, start + immwherestartis a label at the very start of the program andimmis the offset (in bytes) of the instruction you want to jump to.
The two following assembly programs, for example, are equivalent and use beq in the correct manner:
| Option 1 | Option 2 |
|---|---|
|
|
The label at equal points to the same location as an offset of 8 bytes (2 instructions) from a label at start.
Task 2: Test Case Submission
Even with this reduced subset of the RISC-V 64 instruction set, there is still plenty of complicated behavior. We suggest writing many test cases to ensure the correctness of your program.
In addition to your implementation in logic.c, you will submit a test suite in tests.txt.
Each test should begin with a line for the additional command-line arguments: CMDS: <arg_0> ... <arg_n>, followed by the assembly for the test case. The last line should have the non-zero outputs in the same format as the command-line arguments: OUTS: <out_0> ... <out_n>.
For example, the following adheres to this format:
CMDS:
addi ra,zero,0x155
andi sp,ra,0x1b9
OUTS: 1@0x155 2@0x111
CMDS: 8@0xbeef 2@0xbee 9@0xef
addi x8, x8, 9
add x1, x8, x9
add x1, x1, x2
OUTS: 1@0xcbd5 2@0xbee 9@0xef 8@0xbef8
Your tests should cover both basic and edge cases for all of the required instructions. You should have at least 15.
Submission
On Gradescope, submit logic.c and tests.txt.
Rubric
logic.c: 75 pointstests.txt: 25 points
Assembly Programming
Instructions:
Remember, all assignments in CS 3410 are individual.
You must submit work that is 100% your own.
Remember to ask for help from the CS 3410 staff in office hours or on Ed!
If you discuss the assignment with anyone else, be careful not to share your actual work, and include an acknowledgment of the discussion in a collaboration.txt file along with your submission.
The assignment is due via Gradescope at 11:59pm on the due date indicated on the schedule.
Submission Requirements
You will submit the following files to Gradescope. From the lab:
lab.txt: Contains all work from the lab exercises.
From Part I;
arrays.s: implementation of the array manipulation programmult.s: implementation of multiplicationprime.s: implementation of primality checker
From Part II:
mystery1.c: C translation of mysterious function 1mystery2.c: C translation of mysterious function 2
Overview
This assignment will level-up your skills as an assembly language programmer: both reading and writing RISC-V assembly.
Part 0: Lab
During lab section, we will start with some warm-up exercises to get you familiar with writing RISC-V assembly and to help you start with the assignment. To familiarize yourself with the available instructions, see the RISC-V instruction set manual. As you write assembly, you will also likely find it helpful to use 3410 RISC-V interpreter to execute and validate your code.
Submit all your answers to this part as a text file: lab.txt.
This does not need to be formatted in any specific way; just make it readable to a human.
We are just looking for complete answers in this part.
Writing Assembly Programs
Your task in lab is to write RISC-V assembly programs to implement several functions.
1. Arithmetic
We begin with implementing arithmetic functions. The binomial theorem lets you expand the powers of a binomial as the following sum of terms:
(x+y)n=n∑k=0(nk)xkyn−k
We’ll implement both the right- and the left-hand side of this equation for n=4.
Let’s consider what these programs might look like in C. The LHS would look like:
z = pow(x + y, 4)
And you could write the RHS as:
z = 1 * 1 * pow(y, 4) + 4 * x * pow(y, 3) + 6 * pow(x, 2) * pow(y, 2) + 4 * pow(x, 3) * y + 1 * pow(x, 4) * 1
Write two RISC-V assembly programs: one that computes the value of the LHS of the equation and another that computes the RHS.
Then, check that the values given by both are the same for x = 5 and y = 7.
For each program, assume that:
- register
x1holds the value ofx x2holdsyx3holdsz, the final value of the expression
Hint: You can use the mul instruction to implement the calls to pow in the code above.
As an even better alternative, you can use shift instructions to multiply by a number that is a power of two.
So when you need multiply by a constant, see if you can instead write a sum of shifts.
2. Load and Store
Consider this function in C, which swaps the values at indices 1 and 3 in an array of ints:
void swap(int* arr) {
int temp = arr[1];
arr[1] = arr[3];
arr[3] = temp;
}
Assume that the arr pointer is in register x1.
(Also, don’t worry about out-of-bounds accesses: assume that we allocated enough space for the arr array.)
Write the RISC-V assembly code to implement this swap.
3. Conditional Control Flow
Consider this code with a simple if statement:
if (x < y)
y = (x - y) * 2;
else
y--;
Assume that:
- register
x16holdsx x17holdsy
You may use all other registers to store temporary values if you like. Write a RISC-V assembly program to implement this code.
4. Loops
Consider this for loop in C:
for (int i = 0; i < y; i++) {
x = x + 2;
}
return x;
Assume that x and i start at 0, and that we use these register mappings:
yis in registera0xis in registera1iis in registert0
Which of these RISC-V assembly translations are correct? For the incorrect translations, write a brief explanation of why they are incorrect.
Option 1:
for:
blt t0, a0, end
body:
addi a1, a1, 2
addi t0, t0, 1
beq x0, x0, for
end:
Option 2:
for:
beq t0, a0, end
addi a1, a1, 2
addi t0, t0, 1
beq x0, x0, for
end:
Option 3:
bge x0, a0, end
for:
bge t0, a0, end
addi a1, a1, 2
addi t0, t0, 1
beq x0, x0, for
end:
Option 4:
bge x0, a0, end
for:
bge t0, a0, end
body:
addi a1, a1, 2
addi t0, t0, 1
end:
Option 5:
ble a0, x0, end
for:
addi a1, a1, 2
addi t0, t0, 1
blt t0, a0, for
end:
5. Putting Everything Together
Finally, let’s translate the following C program that calculates the product of an array:
void product(int* arr, int size) {
int product = 1;
// --- START HERE ---
for (int i = 0; i < size; i++) {
product *= arr[i];
}
// --- END HERE ---
printf("The product is %d\n", product);
}
Translate the indicated section of code—just the loop—to RISC-V assembly. Assume that:
x1holdsarrpointerx2holdssizex3holdsproduct, and it is already initialized to 1 (outside of your code)x4is uninitialized, but will holdi
Feel free to use any other registers as you see fit.
Reading Assembly
Next, we’ll try understanding assembly code. A good strategy for understanding assembly code is to try reverse translation: write out a C program (or a “pseudo-C program”) that corresponds to the assembly code and then try to understand that code.
6. Branches
Consider the following RISC-V assembly:
addi t0, x0, 0
addi t1, x0, 5
blt t1, x0, label
addi t0, t0, 5
label:
addi t0, t0, 6
What is the value of register t0 after running this code?
To answer this question, you can try writing out the corresponding C program.
If blt were replaced by bge, what would the value of register t0 be?
7. Accessing Memory
Consider the following assembly:
addi t1, x0, 4
addi s2, x0, 7
sw s2, 8(t1)
lw s3, 12(x0)
What is the value of s3 after this code runs?
Again, it can be very helpful to first write the corresponding pseudo-C code. Here’s one way to do that:
int* t1 = 4;
int s2 = 7;
*(t1 + 8) = s2;
int s3 = *(12 + 0);
Why are the constants in those last two lines 2 and 3? (You may want to refresh your memory about the rules of pointer arithmetic in C.)
8. Loop to C
Let’s translate this assembly code back to C:
addi t0, x0, 7
addi t1, x0, 0
loop:
bge x0, t0, end
addi t0, t0, -1
add t1, t1, t0
beq x0, x0, loop
end:
Assume that the value of variable x is held in register t0 and y is held in register t1.
Here’s a partial translation:
int x = 7;
int y = 0;
while (A) {
x = B;
y = C;
}
The placeholders A, B, and C mark expressions that are up to you.
All of these should be C expressions.
Part I: From C to RISC-V
In this first part, you’ll translate three C programs written to RISC-V assembly. Consider trying out your implementations using the online RISC-V simulator to check that it behaves like the original C.
Array Accesses
Imagine we have variables of these types:
int x; // x10
int y; // x11
int* A; // x12
int* B; // x13
Assume that the two pointer variables, A and B, point to large arrays of ints.
The code you need to translate is:
x += (x + y) * 2 - A[4];
B[3] = x;
Assume:
xis stored in registerx10yis inx11- the base address of array
Ais in registerx12 Bis inx13
Use x5 and x6 (and no more) as the temporary registers.
Write your assembly code in a file named arrays.s.
Multiplication
Let’s implement the integer multiplication instruction in RISC-V using other instructions!
The instruction mul rd, rs1, rs2 multiplies rs1 and rs2 and stores the result in rd.
Here is an implementation in C for 64-bit integers:
unsigned long intmul(unsigned long rs1, unsigned long rs2) {
unsigned long rd = 0;
for (int i = 0; i < 64; i++) {
if (rs2 & 0x1) {
rd += rs1;
}
rs1 <<= 1;
rs2 >>= 1;
}
return rd;
}
Translate the above code to assembly.
Do not use the mul instruction.
Assume:
- the variable
rs1is stored in registera0 rs2is in registera1- the return value
rdgoes int0
Use t0, t1, and t2 for any temporary values.
Please name your submission file mult.s.
Primality Test
The following function prime gives a rudimentary algorithm for checking whether a number (p) is prime:
bool prime(int p) {
if (p < 2) {
return false;
}
for (int i = 2; i < p; i++) {
int rem = p % i;
if (rem == 0) {
return false;
}
}
return true;
}
Translate this function to RISC-V.
Submit your file as prime.s.
Please label the entry block to your assembly with .prime.
Imagine that there are two labels .ret_tru and .ret_fls that already exist;
translate the return true and return false lines into jumps to these labels.
Assume p is stored in a2 (a.k.a. x12).
To implement the % operation, you will need to use mul and div instructions.
Please use t3–t6 (a.k.a. x28–x31) for temporary values, and try to minimize how many of these you use.
Part II: Mysterious RISC-V
Your friend, Sia, is a great C programmer. But she doesn’t understand RISC-V assembly, unfortunately. She is trying to understand some mysterious RISC-V programs so she comes to find you, a RISC-V assembly programmer, to help her translate those RISC-V programs to C so that she can understand what they do.
Mysterious Function 1
Here’s one assembly program Sia is trying to understand:
loop:
lw x5, 0(x12)
mul x5, x5, x15
lw x6, 0(x13)
add x6, x6, x5
sw x6, 0(x11)
addi x11, x11, 4
addi x12, x12, 4
addi x13, x13, 4
addi x14, x14, -1
bne x14, x0, loop
ret
Sia has already written a function signature:
void mystery1(int *arr1, int *arr2, int *arr3, int size, int num) {
// ???
}
Assume that the function arguments are in registers x11 through x15, a.k.a. a1 through a5. Also assume that any array length given as an input is greater than zero.
Complete this C function so it behaves the same way as the above assembly.
Follow these guidelines in your translation:
- Prioritize readability. Comments are optional, but use them if you think it makes the code easier to understand.
- Do not use
goto. Use C’sif,for,while, etc. instead. - Prefer
forloops overwhileloops. It is always possible to usewhileto implement any loop, but we want you to useforif the control flow fits the typicalfor (i = 0; i < max; i++)pattern.
It is possible to implement this function in only 2 lines of straightforward, readable C. Your solution does not need to be that short, but try to make it reasonably compact and understandable. (Sia will be grateful!)
Submit your completed implementation of the mystery1 function in mystery1.c.
Hint: Once you have a working C program, consider writing some tests for it. You can write a main function that calls the mystery1 function a few times on different inputs, for example, so you can compare the results to running the original RISC-V code. But please only submit the mystery1 function alone.
Mysterious Function 2
Sia asks you about a second mysterious assembly program:
addi x10, x0, 0
loop:
lw x6, 0(x12)
bne x6, x0, foo
j bar
foo:
sw x6, 0(x11)
addi x11, x11, 4
addi x10, x10, 1
bar:
addi x12, x12, 4
addi x13, x13, -1
bne x13, x0, loop
ret
She already has this function signature:
int mystery2(int* arr1, int* arr2, int size) {
// ...
}
The function arguments are again in registers a1 through a3 (a.k.a. x11 through x13). Register x10 is used to store the result of mystery2.
Complete this function body.
Use the same guidelines as in the previous part. You can also assume that any array length given as an input is greater than zero.
It is possible to implement this code in about 6 lines of readable C but, again, your solution does not need to be that short.
Submit your solution in a file named mystery2.c.
Rubric
We will test all submitted code by running it on several test cases to check that it behaves correctly, i.e., equivalent to the original code. We will also manually read to the assembly code to check that the required registers are used, and we’ll read the C to see that it obeys the guidelines.
- Lab
lab.txt: 10
- Part I
arrays.s: 10mult.s: 10prime.s: 10
- Part II
mystery1.c: 10mystery2.c: 10
Functions in Assembly
Instructions:
Remember, all assignments in CS 3410 are individual.
You must submit work that is 100% your own.
Remember to ask for help from the CS 3410 staff in office hours or on Ed!
If you discuss the assignment with anyone else, be careful not to share your actual work, and include an acknowledgment of the discussion in a collaboration.txt file along with your submission.
The assignment is due via Gradescope at 11:59pm on the due date indicated on the schedule.
Submission Requirements
Please submit the following files.
From the in-lab work:
addone.s: your first assembly function, which just doesi+1recsum.s: a recursive summation function
From Part 1:
recursive.s: implementation for recursive Fibonaccimemoization.s: implementation for memoization Fibonaccitail_recursive.s: implementation for tail recursive Fibonacciopt_tail.s: implementation for tail call optimization
Provided Files
We have provided you:
- a
Makefile recursive.c,memoization.c,tail_recursive.c, andopt_tail.cas the skeleton codecompare.cto run the timing to evaluate different methods
Overview
This assignment will expand your understanding of RISC-V assembly programming with a focus on managing the call stack. You will get direct experience with defining and calling functions, and you will learn about optimizing code for performance.
Part 0: Lab Section
During this lab section, you’ll get some initial experience with writing functions in assembly. The key challenge is in following the RISC-V standard calling convention. The calling convention describes the rules that functions and the code that call them follow so that they can be compatible.
To adhere to the calling convention, all RISC-V functions are composed of a prologue, the function body, and an epilogue. You can start by writing the body, and then note which callee- and caller-saved registers you use in the body. Then, you can write the prologue and epilogue to properly save and restore those registers.
Warm Up: addOne
Let’s start simple by implementing a function that just adds 1 to its argument. You can imagine this C function:
int addOne(int i) {
return i + 1;
}
Start by writing the body.
If you refer to the RISC-V calling convention,
you’ll notice that the first argument and the return value go in register a0.
So the body of this function is pretty simple:
addi a0, a0, 1
Next, write the prologue.
We need to decide how big the stack frame must be; we’ll call that number of SIZE.
It must be big enough to hold the return address, any callee-saved registers, and any local variables that don’t fit in registers.
Here’s a compact “to-do” list for what the prologue must do:
- Move the stack pointer, with
addi sp, sp, -SIZE. - Save the return address to the stack.
- Save any callee-saved registers that our body uses to the stack.
Then, the epilogue does the opposite:
- Restore any callee-saved registers from the stack.
- Retrieve the return address,
ra, from the stack. - Move the stack pointer back to its original position, with
addi sp, sp, SIZE. - Use
ret(a.k.a.jr ra) to return to the caller.
Our function body, as we’ve written it, doesn’t use any callee-saved registers (s0 through s11) or need any stack space for locals.
So the only thing we need to store in the stack frame is the return address.
Pointers in our architecture are 64 bits, so that’s 8 bytes in our stack frame.
Putting it all together, here’s an implementation of addOne:
addOne:
# Prologue.
addi sp, sp, -8 # Push the stack frame.
sd ra, 0(sp) # Save return address.
# Body.
addi a0, a0, 1
# Epilogue.
ld ra, 0(sp) # Restore return address.
addi sp, sp, 8 # Pop the stack frame.
ret
A main part of writing the prologue and epilogue is deciding where in the stack frame to put all your temporary values.
In other words, which offsets on sp will you use to load and store them?
In this function, there’s only one temporary, the return address, so that goes at 0(sp).
But in general, it’s up to you to decide how to lay out the values within your stack frame.
Put your addOne implementation in a file called addone.s.
Trying It Out: Calling Your Function From C
We can’t run this assembly program directly because there is no main function yet.
It also doesn’t print anything out, which would make it hard to tell what it’s doing.
One way to try out your assembly functions is to write some C code that calls them.
Make sure that your addone.s implementation has
an addOne: label at the top.
At the top of the file, add this line:
.global addOne
This directive tells the assembler that the addOne label is a global symbol, so it’s accessible to other code.
Then, write (in a separate file) a short C program like this:
#include <stdio.h>
int addOne(int i);
int main() {
int res = addOne(42);
printf("%d\n", res);
}
That addOne declaration is a prototype, which means it doesn’t have a function body.
It just tells the C compiler that the function is implemented elsewhere—in your case, in an assembly file.
Now, let’s compile and link these two files together. Use a command like this:
$ rv gcc your_assembly_file.s your_wrapper_code.c -o your_test
Then use rv qemu your_test, as usual, to run the linked program.
All this works because of the magic of calling conventions. You and GCC are both “assembly writers,” and because you agree on the standard way to invoke functions, the assembly code you both write can interoperate.
Recursive Sum
Next, we’ll write a recursive function that sums the integers from 1 through n. The function we want to implement would look something like this in C:
int sum(int n) {
if (n == 0)
return n;
return n + sum(n - 1);
}
In assembly, recursive function calls work exactly the same way as any other function call—the caller and callee just happen to be the same function. We’ll follow the RISC-V calling convention in both roles.
Start by writing the function body.
The interesting part is implementing the function call.
Which caller-saved registers do you need to save before the jal instruction and restore after the jal?
Next, write the prologue and epilogue.
You’ll want to start by making a list of all the values this function will ever need to store in its stack frame, including the return address and any local-variable slots.
Decide stack frame layout, i.e., which offsets you’ll use for each value.
Then, follow the recipe from the addOne step above to implement the prologue and epilogue.
Try your function out by writing a main wrapper in C, as we did above.
You’ll want to try calling your sum function on several different inputs.
Put your assembly implementation of sum in a file called recsum.s.
Part 1: Optimizing Fibonacci
In this assignment, you will implement several different versions of a function that calculates numbers in the Fibonacci sequence. We’ll start with a straightforward recursive implementation and then explore some performance optimizations.
Recursive Fibonacci
Here’s a straightforward recursive implementation of a Fibonacci function in C:
unsigned long r_fibonacci(int n) {
if (n == 0)
return 0;
else if (n == 1)
return 1;
else
return r_fibonacci(n - 2) + r_fibonacci(n - 1);
}
Your task is to translate this code into RISC-V assembly.
Put your implementation in a file called recursive.s.
We have provided a main function you can use to test your code in recursive.c.
To test your code, type:
$ rv make recursive # Build the `recursive` executable.
$ rv qemu recursive 10 # Run it.
The recursive executable takes a command-line argument:
the index of the Fibonacci to calculate.
So qemu recursive 10 should print the 10th Fibonacci number, which is 55.
Memoization
The recursive implementation works, but it is very slow. Try timing the execution of a few Fibonacci calculations:
$ time rv qemu recursive 35
$ time rv qemu recursive 40
$ time rv qemu recursive 42
On my machine, calculating the 40th Fibonacci number took 4 seconds, and calculating the 42nd took 11 seconds. That suggests that the asymptotic complexity is pretty bad.
Part of the problem is that the recursive version recomputes the same answer many times.
For example, if you call r_fibonacci(4), it will eventually call r_fibonacci(2) twice:
once directly, and once indirectly via the recursive call to r_fibonacci(3).
This redundancy can waste a lot of work.
A popular way to avoid wasteful recomputation is memoization. The idea is to maintain a memo table of previously-computed answers and to reuse them whenever possible. For our function, the memo table can just be an array, where the ith index holds the ith Fibonacci number. Here’s some Python code that illustrates the idea:
def m_fibonacci(n, memo_table, size):
# Check the memo table. A nonzero value means we've already computed this.
if n < size and memo_table[n] != 0:
return memo_table[n]
# We haven't computed this, so do the actual recursive computation.
if n == 0:
return 0
elif n == 1:
return 1
answer = (m_fibonacci(n - 2, memo_table, size) +
m_fibonacci(n - 1, memo_table, size))
# Save the answer in the memo table before returning.
if n < size:
memo_table[n] = answer
return answer
In C, the type of memo_table will be unsigned long*, i.e., an array of positive numbers.
size is the length of that array.
Here’s the function signature for our new function:
unsigned long m_fibonacci(int n, unsigned long* memo_table, int size);
Implement this m_fibonacci function in RISC-V assembly.
Put your code in memoization.s.
We have provided a memoization.c wrapper that you can use to test your code.
You can use the same procedure as above to try your implementation:
rv make memoization
followed by
rv qemu memoization <number>.
Notice how much faster the new implementation is! Take some number that was especially slow in the recursive implementation and time it using your memoized version:
$ time rv qemu memoization 42
On my machine, that takes just 0.5 seconds. That’s 22× faster!
Tail-Recursive Version
While the new version is a lot faster, it still makes a lot of function calls. Some of those function calls turn out to be fast, because they just look up the answer in the memo table. But we can do better by changing the algorithm to need only one recursive call.
Again using Python syntax, here’s the algorithm for a faster recursive version:
def tail_r_fibonacci(n, a, b):
if n == 0:
return a
if n == 1:
return b
return tail_r_fibonacci(n - 1, b, a + b)
This version is called tail-recursive because the recursive call is the very last thing the function does before returning. Marvel at the fact that this version makes only n recursive calls to calculate the nth Fibonacci number!
Here’s the function signature for this version:
unsigned long tail_r_fibonacci(int n, unsigned long a, unsigned long b);
Implement this tail_r_fibonacci function in tail_recursive.s.
As usual, we have provided a C wrapper so you can test your implementation:
rv make tail_recursive followed by rv qemu tail_recursive <number>.
Tail-Call Optimization
Making n recursive calls is pretty good, but is it possible to optimize this code to do no recursion at all? That would mean that the algorithm uses O(1) stack space instead of O(n).
That’s the idea in tail-call optimization.
The plan is to exploit that, once the recursive call to tail_r_fibonacci is done, the caller has nothing more to do.
The callee puts its return value in a0, and that is exactly what the caller wants to return too.
Because there is no more work to do after the tail call,
we don’t need to waste time maintaining the stack frame for the caller.
We can just reuse the same stack frame for the recursive call!
Implement an optimized version of the tail-recursive Fibonacci algorithm in opt_tail.s.
Instead of using a jal (or call) instruction for the recursive call, you can just use a plain unconditional jump (j in RISC-V).
Be sure to carefully think through when and where you need to save and restore the return address to make this work.
Your function should be named opt_tail_fibonacci,
and it should have the same function signature as the previous version.
As usual, opt_tail.c can help you test your implementation: rv make opt_tail followed by rv qemu opt_tail <number>.
Compare Performance
We have provided a program, in compare.c, that can compare the performance of these various optimizations more precisely than the time command.
(That was also measuring the time it takes to start the executable up, which can be slow, especially when it entails launching a Docker container.)
Build the tool and invoke it like this:
$ rv make compare
$ rv qemu compare <method> <n>
You can give it the name of a method (recursive, memoization, tail_recursive, or opt_tail) and a number n to measure the time taken to compute the nth Fibonacci number.
Or use the all method to compare all the implementations.
When I ran this once on my machine with n=20, it reported that the recursive implementation took about 2.6 seconds, memoization brought this down to just 7 milliseconds, tail recursion was even faster at 3 ms, and the optimized tail call version was blazingly fast at only half a millisecond. Every computer is different, so your numbers will vary, but see if you observe the same overall performance trend.
There is nothing to turn in for this part—it’s just cool!
Rubric
- Part 0
addone.s: 5 pointsrecsum.s: 5 points
- Part 1
recursive.s: 10 pointsmemoization.s: 15 pointstail_recursive.s: 10 pointsopt_tail.s: 15 points
Cache Optimization
Instructions:
Remember, all assignments in CS 3410 are individual.
You must submit work that is 100% your own.
Remember to ask for help from the CS 3410 staff in office hours or on Ed!
If you discuss the assignment with anyone else, be careful not to share your actual work, and include an acknowledgment of the discussion in a collaboration.txt file along with your submission.
The assignment is due via Gradescope at 11:59pm on the due date indicated on the schedule.
Overview
In this assignment, you will explore the effects on performance of writing “cache-friendly” code, i.e., code that exhibits good spatial and temporal locality. The focus will be on implementing matrix multiplication.
Release Code
You are provided with these files:
tasks.c,tasks.h: The matrix multiply functions you will implement. All your programming work happens intasks.c. Do not modifytasks.h.matmult.c: A command-line program (i.e., amainfunction) to run (and time) the matrix multiplication functions.helpers.c,helpers.h: A few utilities for the user interface and allocation.Makefile: A recipe for building and running your code. The Makefile includes a few options to help adjust parameters for your code; we’ll introduce those below.test_matmult.c: Some tests for the matrix multiply functions. Typemake testto build the tests.collect_times.pyandplot_times.py: Scripts to collect and visualize execution times for the matrix multiplication functions.transpose.c,test_transpose.c: Implementation and tests for some matrix transpose functions. You don’t need these to complete your work, but you can use them to try out some examples of matrix-processing functions.
You will only modify tasks.c.
Do not modify any other source-code files.
You will also turn in a discussion.txt file (not provided).
Background: Optimizing for Locality
The performance penalty of a cache miss can be significant, and thus the performance improvement that cache memory offers is greatest when the data we need to operate on remains in the cache for as long as we need it. In the big picture, we want to write code that has good spatial locality: when a data location is referenced, the program will reference nearby locations soon.
There are a variety of techniques to improve the spatial locality of a program and to exploit good spatial locality for improving performance. In this project, you will explore some of these techniques in the context of matrix multiplication, a simple algorithm with a wide variety of real-world applications.
Representing Matrices
To implement matrix multiplication, we need a way to represent these matrices as arrays. In other words, say we have a matrix with m rows and n columns, so m×n total elements. We want to represent this as a C array of length m×n. We therefore need to decide which order to put the elements in. There are two basic options:
- Row major: Element Mij (i.e.,
M[i][j]) is atM[i*n + j]in the array. - Column major: Element Mij (i.e.,
M[i][j]) is atM[i + j*m].
In row-major order, you can visualize all the rows concatenated together, one row at a time. In column-major order, instead visualize the columns being laid out one at a time into the flattened array.
Many programming languages (including C!) have multi-dimensional arrays. Of course, they have to implement them somehow—typically, they pick one of these two styles. In C, multi-dimensional arrays use a row-major order.
The choice of layout can have profound implications for the locality of algorithms that access the matrix.
Matrix Multiplication Refresher
In linear algebra, matrix multiplication is a binary operation on two matrices, A and B. In the product C=AB, each element cij∈C is equal to the dot product of row ai⋆ and column b⋆j. For example, for the n×n matrices A and B:
A=(123456789),B=(111213141516171819)
we have the product:
C=(9021634296231366102246390)
Here is some pseudocode for a function that multiplies two square N-by-N matrices:
void matmult(double A[][], double B[][], double C[][]) {
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
double cij = 0.0;
for (int k = 0; k < N; k++) {
cij += A[i][k] * B[k][j];
}
C[i][j] = cij;
}
}
}
This version loops over all the cells in the output matrix, C, and calculates them one at a time.
To compute the C entry, we access the corresponding row of A and the corresponding column of B.
The innermost loop accumulates the dot product of this row and column.
While this pseudocode uses two-dimensional access expressions like A[i][j], your real code for this assignment will need to exercise direct control over the memory layout.
So the matrices will be ordinary, 1-dimensional arrays, and you’ll access them by calculating the appropriate indices manually, like A[i*N + j].
Access Patterns in Matrix Multiplication
Let’s think about the memory accesses in this function, assuming a row-major layout. Consider the contents of an 8×8 product matrix C, at the point when we have just calculated the value for c22:
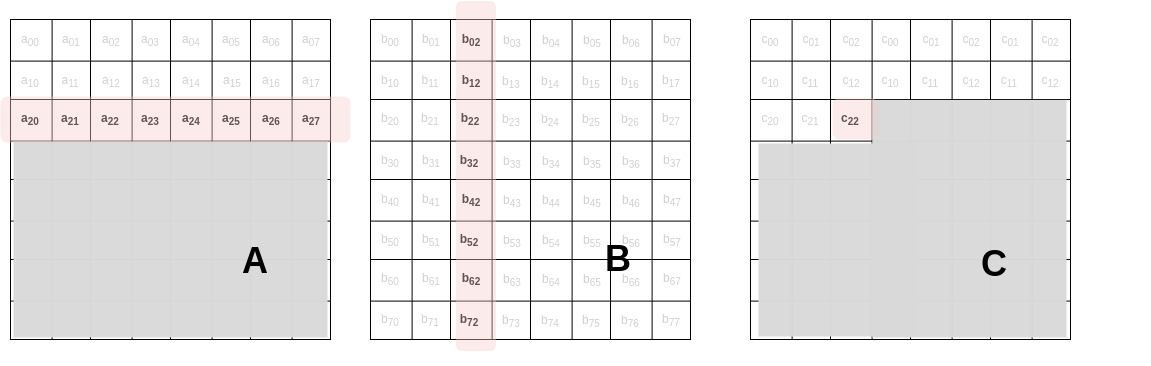
The innermost loop of the algorithm will load the entire highlighted row of A and column of B.
Here’s what that loop looks like if we use a row-major order:
for (int k = 0; k < N; k++) {
cij += A[i*N + k] * B[k*N + j];
}
Think about the way the two array access expressions,
A[i*N + k] and B[k*N + j],
“move” across the iterations of this loop, as we increment k.
The access to A “moves” by 1 element at a time (8 bytes, because we’re using doubles).
The access to B, on the other hand, moves by N elements each time.
We can visualize these accesses in the 1-dimensional realm of memory addresses:

Performance engineers would say that these accesses are strided.
The A access has a stride of 1 element (8 bytes),
and the B access has a stride of N elements (or N*8 bytes).
Which stride seems like it’s probably better for spatial locality? In other words, which access will have a higher hit rate in the processor’s data cache?
Cache Blocking
Blocking or tiling is a strategy for improving the locality of loop-based algorithms. It’s effective when the data you’re processing (e.g., matrices) are so large that they cannot fit entirely into the processor’s cache. The basic idea is to break the problem into smaller blocks that do fit the cache and process them one at a time.
General Strategy
Here’s the general strategy for blocking an algorithm. If your original program consists of d nested loops, then add d more loops at the innermost level. These new loops will process one fixed-size block. Generally, we’ll process the block as if it were a smaller version of the original problem (e.g., a multiplication of two small, block-sized matrices). Then, the original (outer) loops will iterate over all the blocks in the big data structure.
Here’s a 1-dimensional example.
Let A be an array with N elements.
If the original algorithm is:
for i in 0..N:
do_stuff(A[i])
Let’s add blocking, with block size B.
Assuming B is a factor of N for simplicity, there are exactly N/B blocks in N.
So the blocked version would be:
num_blocks = N/B
for block in 0..num_blocks:
for i in (block * B)..((block + 1) * B):
do_stuff(A[i])
The pattern generalizes to two dimensions (i.e., matrices).
Just like the matrices themselves, the blocks will also be 2-dimensional.
If our algorithm starts like this (assuming square N-by-N matrices):
for i in 0..N:
for j in 0..N:
do_stuff(A[i][j])
The blocked version, with B-by-B blocks (again assuming B evenly divides N), becomes:
num_blocks = N/B
for ii in 0..num_blocks: # iterate over row blocks
for jj in 0..num_blocks: # iterate over column blocks
for i in (ii * B)..((ii+1) * B): # rows within the block
for j in (jj * B)..((jj + 1) * B): # columns within the block
do_stuff(A[i][j])
If you want to support the case where B does not perfectly divide N, you will want to use something like min(N, (ii+1) * B) to make sure the inner loops don’t run off the end of the array.
An Example: Matrix Transpose
Consider this implementation of the transpose operation on an n×n matrix, which exchanges the rows and columns:
// Calculate the transpose of M, storing the result in M_t. Both are
// stored in row-major order.
void transpose(int n, double* M, double* M_t) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
M_t[j*n + i] = M[i*n + j]; // M_t[j][i] = M[i][j]
}
}
}
Let’s apply the blocking principle to this loop nest:
void transpose_blocked(int n, double* M, double* M_t) {
int num_blocks = n/BLOCKSZ; // # of block rows & block columns
for (int ii = 0; ii < num_blocks; ii++) { // for every row block
for (int jj = 0; jj < num_blocks; jj++) { // every column block
for (int i = ii*BLOCKSZ; i < (ii+1)*BLOCKSZ; i++) {
for (int j = jj*BLOCKSZ; j < (jj+1)*BLOCKSZ; j++) {
M_t[j*n+i] = M[i*n + j];
}
}
}
}
}
Think about the access patterns in this blocked version.
The matrices themselves consist of N*N*8 bytes;
the blocks are B*B*8 bytes.
If the blocks fit in a system’s cache, but the whole matrices do not, what will the effect on the hit rate be?
We have provided a complete implementation in helpers.c.
Let’s try it out!
Type these commands:
rv make transpose BLOCK=<block size>
rv qemu transpose <matrix size>
We’ve set things up so you provide the block size at compile time and the matrix size at run time. So you can compile the program with a fixed block size and try it with many different matrix sizes. We’ve done this because using a fixed block size lets the compiler do a lot more optimization than it could if the block size were a run-time parameter.
For example, try a block size of 8 and a matrix size of 2048 to start with. (Now would be a good time to ask: How many bytes in a block? How many bytes in these matrices? What is likely to fit in your processor’s cache?)
The program reports the running time for a naive version, a blocked version, and a version with a loop interchange optimization (more on this next). The blocked version, even though there’s a lot more code, should be faster—although the details depend on your computer. When I ran with these parameters, for example, the naive version took 47 ms and the blocked version took 21 ms. Locality matters!
Loop Interchange
Loop interchange is a fancy term for a simple idea: switching the “nesting order” of a loop nest. For some algorithms, just performing this interchange can have a large effect on access patterns and therefore on cache performance.
In general, if you have a loop like this:
for i in 0..m:
for j in 0..n:
do_something(i, j)
Then interchanging the i and j loops would just mean making the j loop the outermost one:
for j in 0..n:
for i in 0..m:
do_something(i, j)
Loop interchange is only correct for some algorithms.
It would not be safe to perform, for example, if do_something(i, j) just printed out the values of i and j;
interchanging the loops would change the output of the program.
The transpose function above, however, is an example where loop interchange is correct,
because every iteration of the innermost loop writes to a different location in the output matrix.
Here’s a version with the i and j loops interchanged:
void transpose_interchanged(int n, double* M, double* M_t) {
for (int j = 0; j < n; j++) {
for (int i = 0; i < n; i++) {
M_t[j*n+i] = M[i*n + j];
}
}
}
Will this version be faster or slower than the original?
Think about the access patterns for the M and M_t accesses in the innermost loop body.
In the original function, the read of M had a stride of 1 element and the write to M_t had a stride of j elements.
In the interchanged version, the strides are reversed.
So this version should be no better or worse than the original.
As we will see in this assignment, however, loop interchange can have a real effect on other algorithms.
Task 0a: Basic Row-Major Matrix Multiply
To warm up, you will first implement, test, and measure some basic implementation of matrix multiplication.
First, implement a row-major matrix multiply in the function matmult in tasks.c.
The function signature looks like this:
void matmult(int n, double* A, double* B, double* C);
The first parameter, n, gives the size of the matrices.
(We will only deal with square matrices in this assignment, so A, B, and C are all n-by-n matrices.)
A and B are both inputs, and C is the output matrix.
To implement this function,
you can follow the pseudocode for matrix multiplication above.
You will need to implement the 2D matrix notation, like A[i][j], with the appropriate index calculations to access the appropriate array entry in row-major order.
Test It
Test your implementation by building and running the provided test_matmult.c.
Try these commands:
$ rv make test_matmult
$ rv qemu test_matmult <size>
Use a matrix size of 2 to begin with, and then try (slightly) larger matrix sizes.
Our test program runs all the implementations of matrix multiplication in this assignment, but those should all just output zeroes for now.
Pay attention only to the first chunk of output for now, which shows the inputs and your matmult’s output.
Use any method you like to confirm that the output matrix is correct:
for example, you could use NumPy’s matmul function.
Measure It
We have also provided code to measure the performance of your matrix multiplication implementations.
Build and run the matmult.c program:
$ rv make matmult
$ rv qemu matmult <size>
Start with a matrix size of 256 or 512 for this performance measurement. The program reports the running time (in milliseconds) for every matrix multiply implementation in this assignment; because you haven’t implemented the later ones yet, those should all take 0 ms. Try a few different sizes to get a sense for how your O(n3) algorithm performs.
Task 0b: Column-Major B Matrix
Next, we’ll implement a variation on the basic algorithm where the B matrix (and only the B matrix) is stored in column-major instead of row-major order.
The other two matrices, A and C, will remain in row-major order.
Our code reformats B for you, so you don’t have to do anything to get it into column-major format—just assume that it comes to you that way.
Implement this version in the matmult_cm function.
You can even copy and paste your matmult function body to get started, and then make any changes necessary to access B in column-major style.
Test your implementation with test_matmult.
The version “with column-major realignment” should match your original implementation’s result.
Try a few different matrix sizes to confirm that it does.
Measure your implementation with matmult.
Compare the running time for the “naive” and “realigned” versions for a few different (larger) matrix sizes.
Finally, write your answers to the following question in discussion.txt, labeled Discussion 0b.
Which is faster: the original “naive” version or your “realigned” matmult_cm?
Try to identify any trend that is consistent across matrix sizes.
Write 1–2 sentences to explain the difference.
Task 0c: Loop Interchange
Apply the loop interchange optimization to your original (all row-major) matrix multiply.
Specifically, interchange the j and k loops.
The order of iteration will therefore be:
- Outermost loop:
i, the row inC. - Middle loop:
k, the column ofAand row ofB. - Innermost loop:
j, the column inC.
Just swapping the order of the loops will not work.
There is more to this task to make sure the matrix multiplication is still correct.
Specifically, if you start with the matrix multiply pseudocode and make j the innermost loop, the variable j won’t even be in scope for the access to C[i][j]!
The general strategy here is to
skip the accumulation into a local variable cij and instead add directly to the output entry (C[i][j] in the pseudocode).
You may assume that C is initialized to hold all 0.0 values as a precondition, so it is safe to accumulate into C without first initializing it yourself.
Put your implementation in the matmult_li function.
Once you have something working, determine the access patterns for the array accesses inside the innermost loop.
How do they differ from the original version?
Using your analysis of the access patterns, make (and write down) a hypothesis about which version will be faster.
Test your implementation to make sure the output matches your first implementation.
(Build and run test_matmult.c to compare all the outputs on a few different sizes.)
Then, measure your performance to check your hypothesis about this version’s performance.
(Build and run matmult.c.)
Finally, answer these questions in discussion.txt.
Label your answers with Discussion 0c.
You only need 1–2 sentences per question:
- Describe the access patterns for the
matmult_lifunction. Characterize the stride length of each array access expression. - How do these access patterns differ from the original
matmultimplementation? - What was your hypothesis about which version was likely to be faster?
- Was your hypothesis correct? Describe the measurements you used to decide.
Task 1: Blocking
The final version of matrix multiplication that you will implement is blocking, a.k.a. tiling.
Your blocked matrix multiply will go in the matmult_bl function in tasks.c.
In helpers.h, we have defined a BLOCKSZ macro.
Use this for the size of the blocks (tiles) that you process:
i.e., you will multiply BLOCKSZ-by-BLOCKSZ square chunks of the matrices, one at a time.
(As we outline in the background section, making this value a compile-time constant, instead of a parameter to the function, lets the compiler do important optimizations.)
Because we’re again assuming row-major order, you can start by copying and pasting your implementation for the basic matmult.
Following the recipe from the background section, you’ll need to do these things:
- Calculate how many blocks you need in each dimension. If the matrices have a size of
nin each dimension and your blocks have sizeBLOCKSZin each dimension, how many blocks do you need in a given dimension? Be sure to consider the case whereBLOCKSZdoes not evenly dividen. - Duplicate the 3 loops, for a total of 6 nested loops. The outer 3 will iterate over the blocks in the matrix, and the inner 3 will iterate over the elements within a single block.
You will also need to reuse one insight from your loop interchanged version.
Instead of accumulating into a local variable like cij in the original pseudocode, you will want accumulate directly into the C matrix (relying on the precondition that it is initialized to zero).
This approach yields a convenient way to combine the results of different blocks.
When your implementation is complete, the inner 3 loops should look a lot like a little “naive” matrix multiply of its own! Indeed, a blocked matrix multiply consists of a bunch of little multiplications of the sub-matrices formed by the blocks.
“Short Circuit” Instrumentation
To make it easier to test your code (and to make it possible for us to grade your blocked implementation), we will add an option to stop the execution after two blocks. You must add this line to your code:
if (check_shortcircuit()) return;
Put this line at the top of the innermost block loop,
which should be before the start of the outermost element loop.
In other words, your implementation should consist of 6 nested loops;
put this at the top of the body of the 3rd loop, before the 4th loop starts.
If you’d like an example, see transpose_bl in helpers.c.
The check_shortcircuit function is defined in helpers.c.
Below, we will show you how to use this instrumentation to see the intermediate results for debugging purposes.
Test It
Because BLOCKSZ is a compile-time constant, testing is a little more complicated than for the other versions of our matrix-multiply function.
Follow these steps:
$ rv make clean # Delete the old version, which may use a different block size.
$ rv make test_matmult BLOCK=2 # Build with a new block size.
$ rv qemu test_matmult 4 # Run with a given matrix size.
Providing the BLOCK=<size> argument to make will define the BLOCKSZ macro in your code.
Then, you can run the compiled code on different matrix sizes without rebuilding.
The “short circuit” option is also compile-time parameter.
To enable it, pass SC=1 to the Makefile.
Try this:
$ rv make clean
$ rv make test_matmult BLOCK=2 SC=1
$ rv qemu test_matmult 4
Look at the output for the “with blocking (shortcircuit)” version.
Many of the entries will be zero.
This is the “intermediate state” of the C matrix after finishing two blocks.
You can use this option to debug your blocked implementation if it produces wrong answers.
Measure It
You also need the BLOCK=<size> argument to measure the performance.
Do something like this:
$ rv make clean
$ rv make matmult BLOCK=4
$ rv qemu matmult 512
Task 2: The Optimal Block Size
Blocking is good for large matrices that do not fit in a processor’s cache.
It is effective because it creates a smaller working set that can fit in the cache.
The optimal choice of the BLOCKSZ parameter, therefore, depends on the size of your computer’s cache.
Let’s empirically measure the best block size on your machine.
We have provided two Python scripts to help run an experiment:
collect_times.py, to take measurements, and
plot_times.py, to draw a graph of them.
First, we’ll measure how long matrix multiplication takes with various block sizes. Run a command like this:
$ python collect_times.py -n 128 -b 1,2,4,8,16,32,64,128
Use -n to specify the matrix sizes to try and -b for the block sizes.
The script will try all combinations of the two lists.
It produces a file runtimes.csv, which you can inspect manually or open in a spreadsheet app if you like.
The second script can plot this data as a line chart.
It requires Matplotlib; you will need to install it with something like pip install matplotlib (but the details depend on your platform; see the installation manual if you need help).
Then, just run:
$ python plot_times.py
The script displays the plot and produces an image in plot.png.
Collect and visualize some data to answer these questions.
Write your answers in discussion.txt, labeled Discussion 2:
- What is the best block size on your machine? (Is it consistent across different matrix sizes?)
- Is there a block size beyond which performance seems to degrade? What does this tell you about the size of your computer’s caches?
Submission
There are two files to submit:
tasks.c, containing your implementations ofmatmult,matmult_cm,matmult_li, andmatmult_bl.discussion.txt, containing your three sets of answers to the discussion questions in Task 0b, Task 0c, and Task 2. Label your answers Discussion 0b, Discussion 0c, and Discussion 2.
We will run your code with our versions of the other source-code files, so do not modify any C code outside of tasks.c.
Rubric
- Implementation: 50 points
- Discussion: 20 points
- Discussion 0b: 5
- Discussion 0c: 5
- Discussion 2: 10
Tiny SHell
Instructions:
Remember, all assignments in CS 3410 are individual.
You must submit work that is 100% your own.
Remember to ask for help from the CS 3410 staff in office hours or on Ed!
If you discuss the assignment with anyone else, be careful not to share your actual work, and include an acknowledgment of the discussion in a collaboration.txt file along with your submission.
The assignment is due via Gradescope at 11:59pm on the due date indicated on the schedule.
Submission
You only need to submit one file to Gradescope:
tsh.c, which will contain your solution to Task 1
Provided Files
tsh.c, which will contain your implementation oftsh. This is the only provided file you should modify.sdriver.pl, a testing tool. It executes a shell as a child process and sends it commands and signals from a trace file. It then captures and displays the output.tshref, which contains an executable that serves as the reference solution fortsh.Makefile, which contains the build commands for this assignment.traces/trace{01-16}.txt, which are designed to test the correctness of your shell.
Overview
Your task in this assignment is to implement a command-line shell. It’s easy to forget that a shell, despite its centrality as the user interface to a computer, is “just another normal program.” It is not part of the kernel, and it does not have any kind of special privileges. It processes commands that you type and then uses standard OS facilities to launch other programs on your behalf.
With this assignment, we hope to demystify how the essential, OS-adjacent parts of a computer system work.
What Is a Shell?
For our purposes, a shell is an interactive command-line interpreter. It prints a prompt, waits for the user to enter a command line on its standard input stream, and then carries out some action that the command describes.
A command is a string, consisting of whitespace-separated words, like ls -l somedir.
The first word (ls in our example) is the command:
either a special built-in command name or the name of an executable file to launch.
The remaining words (-l and somedir in the example) are arguments to pass to the command.
The command receives this list of arguments as strings and can do anything it likes with them.
(That’s what the argc and argv arguments to C’s main function receive.)
In the case of a built-in command, the shell can immediately take some action itself.
Some shell built-ins in “real” Unix shells you may have used before include set, source, exit, and alias.
Most of the time, however, commands refer to actual executable files (i.e., compiled programs) that exist in the filesystem.
ls is the name of an executable file, for example (it is not a built-in command in most shells).
Your shell has a set of directories it looks in to find executables.
(If you want to know where ls lives on your machine, type which ls.)
You can also type the full path to any executable to use it.
On my machine, for example, /bin/ls -l somedir is equivalent to ls -l somedir.
A shell’s main purpose is to launch and manage processes to carry out these shell commands.
In general, a single command might entail launching multiple processes—together, we’ll call this group of processes a job.
For example, you can type ls | head -n 2 to combine the ls and head executables (if you want to see only the first 2 files in a directory);
the job for this command consists of an ls process and a head process with the standard output of the first connected to the standard input of the second.
Background Jobs
Most commands run in the foreground: the shell waits for them to complete before showing you another prompt. Unix shells also support launching long-running commands in the background. This way, you can continue typing other commands while you wait for the background one to finish.
To run a command in the background, put a & at the end.
For example, try typing this in your computer’s “real” shell:
$ sleep 5
The sleep command runs for 5 seconds in the foreground, during which you can’t type any new commands.
Now try this version:
$ sleep 5 &
Your shell will print out some information about the background job it launched, and then it will immediately print another prompt and let you type more commands.
Job Control
Because you can have any number of background jobs running at once, shells provide job control features to manage them. For example:
- To see a list of currently running jobs, type
jobs. - To bring a background job into the foreground, type
fg <job>. - To interrupt the current foreground job, type control-C. (You’ve probably used this one before!)
- To pause the current foreground job and send it into the background, type control-Z.
- To start a paused background job, type
bg <job>.
These job-control features involve sending signals to a job’s processes.
Namely, when you type control-C, the shell sends the SIGINT (“interrupt”) signal to every process in the foreground job.
The processes can choose to handle this signal however they want (or to not handle it at all);
it is only by convention that well-behaved programs exit when they receive SIGINT.
Typing control-C is not the only way to send the SIGINT signal;
for example, you can also send it to a process of your choice by typing kill -s INT <pid>.
Pausing and resuming (control-Z, bg, and fg) uses the SIGTSTP (“terminal stop”) and SIGCONT (“continue”) signals.
Task 0 (Lab): Implementing Test Programs with System Calls
In lab, you will write four C programs that will be extremely beneficial to you as you test your shell implementation:
myspin.c: Sleeps fornseconds in 1-second chunks.myint.c: Sleeps fornseconds and sends SIGINT to itself.mystop.c: Sleeps fornseconds and sends SIGTSTP to itself.mysplit.c: Fork a child process that sleeps fornseconds in 1-second chunks.
These programs will help you test the behavior of your shell while you work on it.
The problem with “normal” programs, like /bin/ls, is that they usually consist of a single process that finishes immediately—so they aren’t very useful for testing the way background jobs behave.
These small programs provide an artificial way to check that your shell’s job-control features work correctly.
These test programs sleep repeatedly for 1-second intervals.
That means making n calls to the C sleep() function in a loop.
The reason is that this strategy will make the programs more responsive to signals—they can handle signals between adjacent sleep() calls.
Step 1: myspin
Create a file called myspin.c.
Include the libraries stdio.h, unistd.h, and stdlib.h at the top of the
file and write the main function:
#include <stdio.h>
#include <unistd.h>
#include <stdlib.h>
#include <signal.h>
int main(int argc, char* argv[]) {
return 0;
}
Build and run your program in the usual way.
Name your executable myspin.
Now, write the main function.
Running rv qemu myspin <N> should sleep for N seconds.
Use the Unix sleep function.
Your program should only sleep in one-second chunks:
i.e., it should only ever call sleep(1).
You may also want to browse the C standard library headers for other useful functions.
Check-in with the TAs once you’ve finished this step.
Step 2: myint
Create a file called myint.c.
You can start with the same header files as in the previous step.
This program should sleep for N seconds (again in 1-second chunks) and then send itself the SIGINT signal (which will cause the process to exit).
You can copy the sleeping-related code from myspin.c.
Use the kill() function from signal.h to send the signal.
(Contrary to the name, the kill() function can send any signal—not just SIGKILL.)
The first argument to the kill() function is the process ID (pid) where the signal should be sent; the getpid() function function can help with this.
The second argument is the signal to send; use the SIGINT macro for this value.
Test your program by building it and then running rv qemu myint 2 or similar.
If you want to check that your program is actually getting interrupted, try this:
$ rv sh -c 'qemu myint 2 ; echo $?'
That uses [the special $? shell variable][exit-var] to check the exit code of the command.
An exit code of 130 means that the process received SIGINT.
Step 3: mystop
Next, write mystop.c.
It should work the same way as myint.c but send the SIGTSTP signal instead of SIGINT.
It is OK to copy code from myint.c.
Build and test your program.
(The exit status should be 0, so myint should appear to behave identically to myspin.)
Step 4: mysplit
Finally, write mysplit.c.
This program should spawn a subprocess that sleeps for N seconds (again in 1-second chunks), and it should wait for that subprocess to exit.
Use the fork() function from unistd.h to launch a subprocess.
Your program will need to behave differently in the parent process and in the child process.
In the child process, use your same old sleep loop to wait for N seconds.
In the parent process, use the waitpid() function to block until the child process finishes.
The waitpid() function takes three arguments: the process ID to wait for,
an “out-parameter” stat_loc for the status of the subprocess,
and an options parameter for extra flags.
You don’t need either of the latter things, so you can pass a null pointer and 0 for them—so waitpid(your_child_process_id, NULL, 0) will suffice.
Build and test your program.
It should work the same way as myspin, i.e., it should sleep for N seconds when you pass N as the command-line argument.
Here’s an idea you can use to check that your myspin is actually launching a subprocess:
$ rv sh -c 'qemu mysplit 5 & (sleep 1 ; ps ax)'
That launches mysplit in the background and then uses the ps command to list the processes running on the machine.
If mysplit is working correctly, you should see two different qemu mysplit 5 processes running with different pids.
If you try this with myspin instead, there should only be one corresponding process.
Task 1: Implement tsh
Your task is to implement a Tiny SHell, named tsh!
Your tsh implementation will have these features:
- The prompt should be the string
tsh>. (This is done for you!) - Handle commands consisting of lists of words, separated by one or more spaces.
The first word is the command name.
The remaining words are the arguments for that command.
If the name is a known built-in command, then
tshshould handle it internally. Otherwise, it assumes that it is the path to an executable file, which it loads and runs in a new child process. (The command must be a filesystem path, like/bin/ls, not just plainls—yourtshdoes not need to have the “path search” feature that full-featured shells have.) tshdoes not need to support pipes (|) or I/O redirection (>and<). (You can try this for an extra challenge if you like!)- Typing control-C or control-Z should send a
SIGINT(SIGSTP) signal to the current foreground job, as well as any descendants of that job (e.g., any child processes that it forked). If there is no foreground job, then these key combinations should have no effect. - If the command line ends with an ampersand
&, thentshshould run the job in the background. Otherwise, it should run in the foreground. - The shell will assign a job ID (jid) to each job it launches.
This jid is distinct from the process ID (pid) that the OS kernel assigns automatically to every new process.
The shell will assign jids itself in sequential order.
(We have provided all the functions you need to maintain the job list and jids: see
addjob, for example.) When the user refers to jobs on the command line, use a%prefix: for example,%5denotes jid 5. In contexts where both jids and pids are allowed,%5is a jid and5means pid 5. - Support these built-in commands:
exit: Terminate the shell.jobs: List all background jobs. For the exact output format, try runningjobsin the reference implementation. Each line should look like[jid] (pid) Running <command>.bg <job>: Resume<job>(which may be either a pid or a jid) by sending it the SIGCONT signal. Let the job run in the background.fg <job>: Resume<job>as above, using SIGCONT, and then make it the foreground job. Foreground jobs can receive input from the user, so typing characters should send them to the current foreground job.
tshshould reap all of its zombie children. When a process exits, it remains in the kernel’s process table. You will need to usewaitpidon all children to “reap” these zombies. You can detect that a child process was a zombie using theWIFEXITEDmacro (see the manual page forwaitpid); then, remove it from your shell’s job list.- If any job terminates because it receives a signal that it didn’t handle,
then
tshshould recognize this event and print a message with the job’s pid and a description of the offending signal. The message should look likeJob [jid] (pid) terminated by signal <n>. For examples, try the reference implementation.
Functions to Implement
You will need to write these functions, all in tsh.c:
void eval(char* cmdline): Evaluate a given command line.int builtin_cmd(char** argv): If the command is a built-in command, execute it immediately. Otherwise, do nothing.void do_bgfg(char** argv): Execute the built-inbgandfgcommands.void waitfg(pid_t pid): Block until processpidis no longer the foreground process.void sigchld_handler(int sig): The kernel sends aSIGCHLDto the shell whenever a child job terminates, stops because it received a SIGSTOP or SIGTSTP signal. This handler should clean up child jobs which have terminated.void sigint_handler(int sig): The kernel sends aSIGINTto the shell whenever the user typesctrl-cat the keyboard. Catch it and send it along to the foreground job.void sigstp_handler(int sig): The kernel sends aSIGSTPto the shell whenever the user typesctrl-zat the keyboard. Catch it and send it along to the foreground job.
The division of labor between the first four functions is largely a suggestion. It is possible to implement all of the logic in eval, but we do not recommend this as it will be much harder for you to track down bugs and fix them. Separate the functionality between built-in commands, bg/fg, and other helper functions.
Hints
Helper Functions and APIs
There are many helper functions in tsh.c intended to help you manipulate command-line strings and the job list. Do not re-invent the wheel! Read the code and the functions we’ve provided before you start.
In addition, these functions (defined in signal.h, sys/wait.h, and/or unistd.h) will come in handy:
waitpid: waits for a child process to terminate. Note theWUNTRACEDandWNOHANGoptions; they will be useful.kill: sends a signal to a process or set of processesfork: creates a child processexecve: executes a programsetpgid: sets process group IDsigprocmask: sets blocked signals for the calling process
The manual pages for these functions have a lot of detail about how to use them.
One of the tricky parts of this assignment is deciding the allocation of work between waitfg and the sigchld_handler functions. Recall that waitfg blocks until process pid is no longer the foreground process, and sigchld_handler cleans up terminated child jobs when a SIGCHLD signal is received. We recommend doing this:
- In
waitfg, use a busy loop around thesleepfunction. - In
sigchld_handler, usewaitpidto check whether a process has stopped (either suspended, terminated, or exited).
Other solutions are possible, but they can get confusing.
Ideas For Handling Signals
In eval, the parent must use sigprocmask to block SIGCHLD signals before
it forks the child, and then unblock these signals, again using sigprocmask after it
adds the child to the job list by calling addjob. Since children inherit the blocked
vectors of their parents, the child must be sure to then unblock SIGCHLD signals
before it execs the new program.
Basically, all sigprocmask does is take a collection of signals and add them to a blocked
set or an unblocked set. Why would we want to do this? In general, sometimes it is important to
block signals in a critical section of code. In our case, we have a concrete example: the parent
needs to block the SIGCHLD signals in this way in order to avoid the race condition where the
child is reaped by sigchld_handler (and thus removed from the job list) before the parent
calls addjob.
When you implement your signal handlers, be sure to send SIGINT and SIGTSTP signals to
the entire foreground process group. The kill function’s first argument, pid,
can be positive or negative: positive numbers kill a single process, and negative numbers kill
an entire process group. Use -pid here.
When you run your program from a standard Unix shell, your shell is running in the foreground
process group. If your shell then creates a child process, by default that child will also be a
member of the foreground process group. Since typing control-C sends a SIGINT to
every process in the foreground, typing control-C will send a SIGINT to your shell, as well as
every process that your shell created, which obviously isn’t correct. Here is the workaround:
after the fork but before the execve, the child process should call setpgid(0, 0),
which puts the child in a new process group whose group ID is identical to the child’s pid.
This ensures that there will only be one process, your shell, in the foreground process group. When you
type control-C, the shell should catch the resulting SIGINT and then forward it to
the appropriate foreground job.
When your shell receives SIGCHLD, this means that something happened in one of the jobs that you
launched: the job either suspended, resumed after being suspended, was terminated, or exited normally. Unfortunately, there is no direct way to determine which job caused the SIGCHLD signal to raise. It might be the foreground job or it might be a background job that has exited or been terminated (“zombies”). However, given a job’s PID, you can tell what happened to it, using waitpid. Be sure to reap all child processes, i.e., call waitpid eventually on all processes, both the foreground job and the background zombies. You don’t need to worry about handling SIGCHLD signals that come from re-started jobs, since they’ll exit on their own (or be terminated) later.
Ideas For Debugging
If you ever want to explore how a given feature “should” work, you can try it in a
“real” shell like bash or zsh, or run the reference shell we’ve provided (called tshref).
It is also a very good idea to try out your shell by hand, rather than relying ony on the shell driver and trace files (see below). While successful runs of those provide evidence that your solution is correct, they don’t help much when you need to find and fix a bug. Instead, try running your solution directly, with verbose mode turned on — rv qemu tsh -v — and trace the commands that are in one of the traces/trace*.txt files (ignoring the “echo” commands, of course, as well as the ones in all caps, which are just used by the sdriver.pl script). Specifically, look at the displayed response after you type each command.
Also, this is a setting in which your best bet is to add “scaffolding”, i.e. printf statements that
help you to see the control flow of your program, as the more structured debugging with GDB will be
difficult to use. When you do this, be sure to flush your output right away (fflush(stdout)); otherwise, the execution of parent and child processes won’t necessary display your statements when you expect them. In addition to adding these in your tsh.c code, try scaffolding some or all of your Task 0 programs, particularly myspin.c.
If you want to test your shell on certain executables like ls or echo, you can obtain the path to the binary by typing the command which ls in your “real” shell.
(tsh does not support automatic path searching, so you need to type the full path to the ls executable file.)
Finally, programs such as more, less, vi, and emacs do strange things with terminal settings.
Don’t run these programs from tsh—stick with simple text-based programs like ls, ps,
and echo.
Running and Testing
We have provided some tools to help you check your work.
Reference Solution
The executable tshref is the reference solution
for your shell. Run this program to resolve any questions about how your shell should
behave. Your shell should emit output that is identical to the reference solution
(except for pids, which the OS assigns and will change from run to run).
Use rv qemu tshref to run this reference implementation.
Shell Driver and Trace Files
The sdriver.pl program executes a shell as a child process,
sends it commands and signals as directed by a trace file, and captures and displays the
output from the shell.
It is useful for testing your shell with a series of actions that would be tedious to type by hand.
Use the -h argument to learn about the usage of sdriver.pl:
$ rv ./sdriver.pl -h
Usage: /root/./sdriver.pl [-hv] -t <trace> -s <shellprog> -a <args>
Options:
-h Print this message
-v Be more verbose
-t <trace> Trace file
-s <shell> Shell program to test
-a <args> Shell arguments
-g Generate output for autograder
We have also provided 16 trace files (trace{01-16}.txt) that you will use
in conjunction with the shell driver to test the correctness of the shell. The
low-numbered trace files do very simple tests, and the higher-numbered traces
do more complicated tests.
We recommend that you use the trace files to guide the development of your shell.
Start with trace01.txt, and make your tsh produce identical output to our tshref reference implementation.
Then move on to trace02.txt, and so on.
Let’s try running one trace file on your shell, tsh,
and then on our reference implementation, tshref.
The commands for trace01.txt look like this:
$ rv ./sdriver.pl -t trace01.txt -s tsh -a "-p" # Use your `tsh`.
$ rv ./sdriver.pl -t trace01.txt -s tshref -a "-p" # Use `tshref`.
We have provided a Makefile that makes these commands faster to type. Use these targets:
$ rv make test01 # Use your `tsh`.
$ rv make rtest01 # Use the reference `tshref`.
Look inside the trace files to understand how they work.
Most lines are commands to run in the shell.
There are special lines like SLEEP and INT that tell the driver to take certain actions, such as waiting or sending a signal to the shell process.
INT simulates a control-C, and TSTP simulates a control-Z.
Submission
Submit your tsh.c via Gradescope.
Rubric
- 40 points: Correctness on the given traces
- 60 points: Correctness on additional, grading-only traces
Concurrent Hash Table
Instructions:
Remember, all assignments in CS 3410 are individual.
You must submit work that is 100% your own.
Remember to ask for help from the CS 3410 staff in office hours or on Ed!
If you discuss the assignment with anyone else, be careful not to share your actual work, and include an acknowledgment of the discussion in a collaboration.txt file along with your submission.
The assignment is due via Gradescope at 11:59pm on the due date indicated on the schedule.
Submission Requirements
Please submit these files via Gradescope:
barrier.c, which is your implementation of a thread barrier.hash_table.c, which is your implementation of a concurrent hash table.lab.c, which is the lab activity.readers-writer.c, which is your implementation of a readers-writer lock.spinlock.c, which is your implementation of a spinlock.wait-broadcast.c, which is your implementation of wait and broadcast for a condition variable.
Restrictions
- You may not use any additional
#includedirectives. Including libraries such aspthread.h(excluding its use in the test files) orsyscall.hwill result in a score of zero on this assignment. (The point of this assignment is to implement some of the functionality of these libraries yourself, so it is critical that you do not use them in your solution.) - As always, do not change other files (outside of the ones you turn in, listed above). We will use the original versions of these files for grading, so our grading results will not reflect any changes.
Provided Files
The following files are provided in the release:
lab.c, the lab activity.{barrier, hash_table, readers-writer, spinlock, wait-broadcast}.c, which includes the necessary function signatures and#includedirectives.{barrier, hash_table, readers-writer, spinlock, wait-broadcast}.h, the above’s header file.test_{barrier, hash_table, readers-writer, spinlock, wait-broadcast}.c, which provides the structure for testing the above.Makefile, which will appropriately compile and link the above to produce an executable,test_<construct>.
You can find these files in your personalized repository on GitHub.
Overview
In this assignment, you will implement synchronization primitives: the fundamental building blocks of all parallel programming. Some of these will require writing inline assembly to use RISC-V’s LR and SC atomic instructions. Then, you will use the synchronization primitives to create a concurrent hash table.
The purpose of this assignment is to learn how threads and synchronization actually work by implementing the basic building blocks yourself. For that reason, you may not use existing libraries such as the POSIX threads library.
Task 0: Introduction to Inline Assembly
As stated in the overview, inline assembly will be necessary for implementing certain synchronization primitives. As part 0 of this assignment, in lab, you will work through some exercises on writing inline RISC-V assembly.
Inline assembly lets you mix some assembly code into your C programs. You can even exchange data between C variables and registers in assembly. It can be useful for situations where you know exactly what assembly code you want, and C doesn’t have a construct that generates that code. That’s the case for the synchronization primitives in this assignment, which require careful use of RISC-V’s atomic instructions.
Structure
Use this syntax to add inline assembly to your C code:
__asm__ volatile(
// Assembly instructions
: // Output operands
: // Input operands
: // Clobber list
: // Goto list
);
The volatile keyword instructs the compiler to avoid “optimizing your code away,” so the instructions appear verbatim in the compiled program.
The first thing in the parentheses is the assembly code itself.
Then, the lists after each colon describe how the assembly code interacts with the rest of the program:
- The first two rows are for inputs and outputs. These specify the variables that the inline assembly will interact with.
- The third row is for the clobber list. This list describes to the compiler what the assembly code (might) overwrite. For RISC-V, this list can contain register names and the special name
"memory"to indicate that the assembly writes to memory. - Finally, the fourth row is to inform the compiler of the list of
gotolabels used in the assembly.
Here’s an example that calculates and returns a+3b:
int a_plus_3b(int a, int b) {
int result;
__asm__ volatile(
"slliw t0, %2, 1\n"
"addw t0, t0, %2\n"
"addw %0, t0, %1\n"
: "=r" (result)
: "r" (a), "r" (b)
: "t0");
return result;
}
Notice that the assembly code uses placeholders like %0 and %1 in places where register names (like x17 or a1) would usually appear.
These placeholders let the assembly code refer to C variables:
%0refers to the first operand that appears in the:-delimited lists below the assembly code. In this case,result.%1is the second operand,a.%2is the third operand,b.
Then, the three lines after the assembly code describe how it uses registers.
The r in these lines indicate a variable that should be placed in a general-purpose register.
The = means that the assembly will write to that register.
(These are called constraints and constraint modifiers.)
Here’s what the three lines mean:
- The first line is the output operands.
"=r" (result)says that the C variableresultshould be placed in a register so the assembly code can write to it. - For the input operands,
"r" (a), "r" (b)makes the argumentsaandbavailable in registers. - The third line is the clobber list. We include
t0here to indicate that the assembly code overwrites registert0. When you write inline assembly, remember to list all the registers that the assembly writes to. - We omit the
gotolist because our assembly does not use any labels.
Beyond r and =, some other basic constraints and constraint modifiers are:
m: The operand lives in memory.f: The operand lives in a floating point register.i: The operand is a constant integer (immediate).F: The operand is a constant floating point number.+: The operand is both read from and written to.&: The operand is written to before all (note: not any) operands have been read.
Exercises
Complete the functions in lab.c by writing inline assembly.
These two exercises are independent from the rest of the assignment, but they will be useful. They should be submitted together in a file lab.c. Do not change the function signatures.
You can compile lab.c with this command:
$ gcc lab.c -pthread -o lab
Atomic Increment
This is a function that atomically adds 1 to an integer variable in memory, var, and returns its original value.
“Atomically” means that other threads cannot interfere with the increment:
they cannot change the variable between the load and store.
For example, it should be impossible to have two threads simultaneously increment the variable and both read the same original value, leading to lost updates.
This kind of lost update is possible with a normal, non-atomic implementation (load, add 1, store),
so you must use RISC-V’s atomic instructions (lr and sc).
Atomic increments ensure that each thread sees a consistent and up-to-date value of the variable in concurrent environments.
Compare-and-Swap
This function implements the CAS operation, which atomically compares the current value of an integer var with an expected value old. If they are equal, it updates var to a new value new. The CAS operation ensures thread safety by preventing race conditions, as it guarantees that the update occurs only if no other thread has modified var in the meantime. The function returns true upon a successful swap and false if the current value did not match the expected value. A correct implementation will utilize the lr and sc instructions.
Task 1: Spinlock
A spinlock is an implementation of mutual exclusion where a waiting thread repeatedly checks if the associated lock is available. This is called “spinning” or “busy waiting.” Here you will implement the two functions of a spinlock:
spin_lock()to obtain the lock: spin until the lock becomes free, and then acquire it. (The lock may be free already, in which case your spin loop should exit immediately.)spin_unlock()to release the lock.
Each lock is represented as an int*.
Use the int in memory to store a value that indicates whether the lock is free or held by some thread.
The purpose of the keyword volatile is to tell the compiler that other threads may be concurrently modifying the variable.
Hint: Any correct solution will use the RISC-V atomic instructions lr and sc.
Using “ordinary” loads and stores cannot guarantee that memory updates will be visible to other threads in order.
Task 2: Condition Variable (Wait & Broadcast)
Monitors or condition variables are a concurrency mechanism where threads can wait for a condition to become true. Other threads can wake up the waiting threads by broadcasting a signal when the condition changes.
To use a condition variable, a program always pairs it with a lock. For example, imagine a program that uses a queue data structure to keep track of work to do. The program would use a lock to protect the queue, so any thread that pushes or pops the queue must hold the lock while it does so. Now, imagine that some “worker” threads want to wait for the queue to become nonempty: when some work becomes available to do. The program could use a condition variable that indicates when the queue is nonempty. When any thread pushes new work into an empty queue, it would broadcast a notification to all the waiting threads that the condition has changed.
There are two functions for you to implement here:
wait(lock, condition). The first argument,lock, is a spinlock as you implemented it in the previous task. The second argument,condition, is the condition variable (a pointer). The function should immediately releaselockand then wait for another thread to callbroadcast(condition)on the same condition variable. When that happens, acquirelockagain and return.broadcast(condition). Calling this should wake all threads waiting on the associatedcondition.
One possibly counterintuitive aspect of this API is that, while condition must be a pointer to valid memory, the value it points to isn’t important.
It would be OK for this value to always be zero, for example.
The actual logical condition (e.g., “the queue is nonempty”) is generally stored in some other application state.
Use your spin_unlock and spin_lock functions to release and acquire the lock in wait.
Then, to sleep until another thread calls broadcast, you must put the thread to sleep using a system call instead of spinning.
While you usually make system calls via functions in the C standard library,
you are not allowed to do so this time (recall that you may not import any additional headers).
Instead, you must use inline RISC-V assembly to perform the system call.
Refer to the lecture notes on using the ecall instruction to perform system calls.
You must also determine the appropriate Linux system calls to make.
See the syscalls manual page for a complete list.
Then, look at the unistd.h header from Linux or this searchable list (under the “riscv64” column) to find the system call number for the call you want to use.
A good place to start would be the futex syscall, which provides a wide variety of sleeping/waiting functionality.
Task 3: Barrier
When a thread encounters an n-thread barrier, it must wait for n threads to reach the barrier to continue. Barriers are especially useful for bulk synchronous parallelism, where many threads coordinate to work on a problem in coarse-grained steps.
Aside from initializing the barrier, there is one function to implement:
barrier_wait(barrier): If the thread that calls this is the nth to reach the barrier, all threads waiting at this barrier should be awoken. Otherwise, this thread should be put to sleep.
We have provided a barrier struct (see barrier.h) that holds information like n and the current number of threads waiting for the barrier.
You can (and probably should) use your spinlock and condition variable (wait and broadcast) functions to implement your barrier.
Ensure that waiting threads go to sleep instead of spinning.
Hint: If you use your functions from previous tasks, it is possible to implement the barrier correctly in pure C, without any inline assembly.
Task 4: Readers-Writer Lock
In parallel programs, we should be able to distinguish between critical and non-critical actions: those that need synchronization and those that don’t. For example, in the case of reading from and writing to a data structure, parallel writes can lead to race conditions, but parallel reads can be safe. If many threads just need to read the same data concurrently, it is needlessly slow to serialize them.
A readers–writer lock embodies this distinction. Like your basic spinlock, threads will acquire and release the lock to synchronize. Unlike the spinlock, threads must distinguish between acquiring the lock as a reader vs. acquiring the lock as a writer. Multiple threads should be able to read from the lock-protected data in parallel, but only one thread should be able to write to it at a time. And while one thread is writing, no other threads may be reading or writing.
You will implement a write-preferring policy. This means that, when there is a writer waiting to acquire the lock, no new readers can acquire it.
Aside from initializing the readers-writer lock, there are four functions to implement:
start_read()to acquire the lock as a reader, requesting permission to read the protected data structure. If there is an active writer, then sleep until the writer releases the lock.end_read()to release the lock after astart_read(), indicating that its read operation is completed.start_write()to acquire the lock as a writer. If there are are active readers or writers, then sleep until there are none.end_write()to release the lock after astart_write().
We have again provided a rw_lock struct in readers-writer.h with all the data you need to construct a readers–writer lock.
As in the previous two tasks, put waiting threads to sleep instead of spinning.
You will again want to use spin_lock and spin_unlock to protect the data within the rw_lock struct itself,
but be sure that (for example) threads that call start_read while there is an active writer go to sleep.
Use any of your implementations from the previous tasks to implement the readers–writer lock. It is again possible to do this in pure C, without inline assembly.
Task 5: Concurrent Hash Table
Finally, you will implement a hash table that allows for insertion, deletion, and parallel accesses. This hash table handles collisions via separate chaining (i.e., each bucket is a linked list, and a node is added to the linked list upon insertion of a new key).
The idea with a concurrent hash table is that it is safe to use in parallel threads. That is, multiple threads are allowed to concurrently insert, look up, and delete values without holding any locks themselves. The concurrent hash table performs all necessary synchronization internally. It guarantees that all of the operations happen atomically: for example, while one thread is inserting a value into the table, no other thread can observe an inconsistent intermediate state.
Your task is to use any of your synchronization primitives from the previous tasks to implement a concurrent hash table. Aside from initializing the hash table, there are four functions to implement:
cht_insert()to insert a key/value pair into the hash table.cht_delete()to remove the node with the specified key from the hash table.cht_get()to return the value in the hash table associated with a specified key. If there is no such key, returnINT_MIN.thread_cht_requests(), for testing (explained below).
The focus of this assignment is the synchronization primitives, so we have kept this hash table simple:
the keys and values are both of type int.
The hash table does not resize; it has a constant number of buckets.
Test Function
The thread_cht_requests() function is for testing your hash table.
It is used in test_hash_table.c.
That program launches several concurrent threads that all run thread_cht_requests().
The idea is that thread_cht_requests() receives a queue of operations to perform.
It should repeatedly dequeue operations (cht_request values) and perform them:
i.e., look at request.op, which is one of CHT_INSERT, CHT_DELETE, or CHT_GET, and call one of your cht_* functions accordingly.
Our test program works by reading a list of requests from a file and then adding them to this queue for processing.
The test program, test_hash_table.c, creates several threads that all run your thread_cht_requests() function.
Because of the way the pthreads library works, the argument and return value to this function have type void*,
but the argument will be a pointer to a cht_thread_arg struct (and the return value is ignored).
This struct has a pointer to a cht_request_queue that contains the operations that the threads should perform.
Your thread function should repeatedly call dequeue_cht_request to obtain a request and then perform the indicated hash table operation.
To understand more about how thread_cht_requests() should behave, you can see how it is used during testing in test_hash_table.c.
Running and Testing
For each synchronization primitive in this assignment, we provide a file named test_<primitive>.c.
It contains an empty function thread_function(), where you can write some code to test your primitive.
The program launches some number of threads (given on the command line), each of which runs thread_function().
You should add code there that calls your synchronization function repeatedly and ensures that the threads interact in the way you want.
You can compile these programs by running make <primitive>.
The executable then takes one command-line argument for the number of threads.
Do not submit these files; they are only for your own testing.
The test program for Task 5 is a little different;
it calls the thread_cht_requests() function in your hash_table.c.
This function is a required part of this assignment.
Notice also that test_hash_table.c uses your implementation of barriers to synchronize threads.
Submission
On Gradescope, submit barrier.c, hash_table.c, lab.c, readers-writer.c, spinlock.c, and wait-broadcast.c.
Assignment 11: Parallel Raycasting
Instructions:
Remember, all assignments in CS 3410 are individual.
You must submit work that is 100% your own.
Remember to ask for help from the CS 3410 staff in office hours or on Ed!
If you discuss the assignment with anyone else, be careful not to share your actual work, and include an acknowledgment of the discussion in a collaboration.txt file along with your submission.
The assignment is due via Gradescope at 11:59pm on the due date indicated on the schedule.
Submission Requirements
Submit these files to Gradescope:
raycaster.c, with your implementations for 3 functions:raycast_sequential, a sequential implementation of the 2D raycasting algorithm.raycast_parallel_lights, a version that parallelizes the algorithm by light source.raycast_parallel_rows, which parallelizes the algorithm by image row.
test_raycaster.c, with some tests for your implementations- Optionally,
images.zipwith the additional images to go along with those tests, if they use any. raycast_writeup.pdf, a report describing the results of some performance experiments.
Provided Files
You will find these files in your GitHub repository:
raycaster.handraycaster.c, which include function definitions for you to implement. It is OK to add helper functions here.test_raycaster.c, which includes some tests ofraycaster.c. You will extend these tests.main.c, a basic entry point that runs your raycaster on an input image and produces an output image file. This can be useful as a simple test so you can see visually what your implementation is producing.timing.c, which includes amainfunction that can time your implementations of raycasting. You can modify this file—in particular, consider changing the constants at the top—but you will not turn it in.raycaster_util.handraycaster_util.c, which include critical helper functions for the raycaster. Use these functions in your implementation! Resist the urge to reimplement any of this functionality—these math routines can be subtle to get exactly right, so using this provided code will help your code behave predictably and pass the tests. (There is also atest_raycaster_util.cprogram, which you do not need to modify.)image.handimage.c, which provide utilities to manipulate raw image files. Only pay attention toimage.hto understand how to use these utilities; you shouldn’t need to look at the implementation. (We also includestb_image_write.handstb_image.h, from a public-domain set of C utilities).
Overview
Raycasting is a technique for rendering 2D and 3D graphics. Among many other uses, raycasting was the underlying technique that early 3D video games used to produce 3D scenes from 2D level maps. If you’ve ever played an old 3D game where you can move around but you can’t look up or down, it may have used raycasting.
One of the cool things about raycasting is that it is amenable to parallel implementation. Parallelizing the algorithm can be critical for getting it to render images quickly enough for real-time interaction.
Your task in this assignment is to implement the original sequential algorithm and then parallelize it to make it go faster. You will try two different parallelism strategies, measure their differences in performance, and report on your observations.
Background
To render an image, computer graphics techniques start with some data about the scene: light sources, the camera or viewpoint, objects in space. The general category of ray tracing algorithms works by imagining many rays projected in straight lines outward from the camera or from lights. You can then find the first object that each ray “hits” to determine what should be visible or illuminated along that ray.
In this assignment, we will trace rays emitted from light sources. Think of following the path of imaginary photons as they leave the light in all directions. For every light source and every other point in the scene, the light illuminates the point if there are no solid obstacles in between. Here’s a diagram showing the idea:
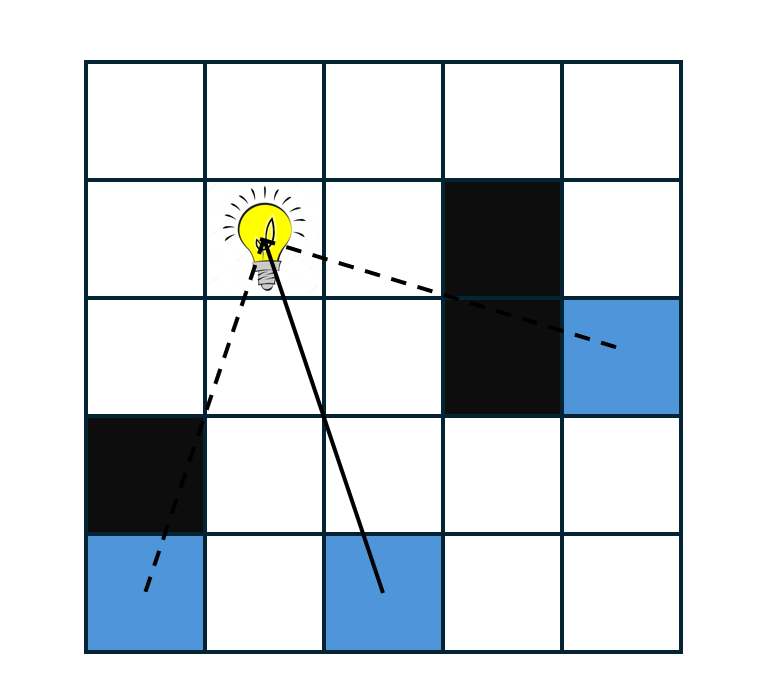
This diagram shows a grid of pixels, one of which has a light source. We have also highlighted three other pixels. Only one (the one with the solid ray) is illuminated; the other rays are occluded by objects in the scene.
In this assignment, we will implement an algorithm to compute the illumination of every point in a scene. We will only consider direct rays: so no reflections or other effects that would require simulating how light “bounces” off of objects.
The effect will look something like this:


The left image is the input scene, where dark pixels are solid obstacles. The right image shows the result of lighting the scene with three lights of different colors in different positions. The light “passes through” lighter-colored pixels and stops at the obstacles.
Images
A raster image is a 2D array of pixels, each of which has a color. An extremely common way to represent colors is with three 8-bit integers for the red, green, and blue components.
See the image.h file for definitions of the Color and Image structs that reflect this strategy.
The Image struct is a wrapper around a row-major array of Colors.
We have also provided utilities to read and write images in the ubiquitous PNG format.
Illumination
Your work on this assignment will add lighting effects to raster images. The main task is to compute the illumination for every pixel in the image: how much the pixel is lit by the light sources in the scene.
For an unobstructed pixel (i.e., there is not a solid object between the pixel and the light source), here is a formula for the illumination of that pixel by that one light:
illumination=(light color)×e−(distance to light)2light strength
This formula makes illumination decay with distance.
The color and strength are intrinsic properties of the light source.
(The raycaster_util.h header defines a Light struct with these fields.)
Multiplying a color by a number scales its intensity by multiplying the red, green, and blue components by the same amount.
We have provided an implementation of this function as the illuminate function in raycaster_util.c.
Remember that this illumination formula is only relevant when there is no occlusion (no obstacle between the light and the given pixel).
A single pixel may be illuminated by multiple light sources.
Use the add_colors function from image.h to combine the illumination from multiple lights.
The Input Scene
In general, there are many ways to specify the scene data for a renderer. In our setup, the scene comes as an image, where light pixels represent free space and dark pixels are solid obstacles. Specifically, a pixel is a solid obstacle if:
red+green+blue<10
We have provided an implementation of this formula as is_obstacle in raycaster_util.h.
Casting Rays
The core of the algorithm is the occlusion check: for a given destination pixel and a given light, check every pixel on a line segment between the destination and the light for a solid obstacle.
The idea is to iteratively move along this line segment by some distance, one step at a time:
next pixel=current pixel+direction×distance
This strategy requires the direction (i.e., angle) from the destination pixel and the light source. Let the destination pixel be (i,j) and let the light be at (x,y). Recalling our trigonometry classes, we can calculate the direction as:
direction=atan(y−jx−i)
We have provided an implementation of this formula as direction_pair in raycaster_util.h.
This step-by-step strategy also requires a distance.
We want to step in the calculated direction just far enough to reach the next pixel.
We have implemented the distance calculation in a function called step (also in raycaster_util.h), which moves from an input pixel in a given direction to a neighboring pixel.
To trace a ray, iteratively call step to test every pixel on the line segment between the light and the destination pixel.
The light-source pixel itself is always illuminated.
Pixels containing solid objects are never illuminated.
Task 1: Sequential Raycast Implementation
Your first task is to implement the 2D raycasting algorithm described above.
Implement the raycast_sequential function in raycaster.c:
Image* raycast_sequential(Image* scene, Light* lights, int light_count);
This function takes in an input image that describes the scene and an array of light sources. It produces a rendered image of the same size.
For every pixel (i,j) in the image, compute the illumination of that pixel for every light. Remember to handle occlusion, i.e., do not include contributions from lights that have a solid obstacle “in the way.”
Let the original color of a given pixel in image be called orig.
Call the combined illumination color, across all lights, illum.
The final output color of that pixel in image should be mul_colors(illum, orig).
(The mul_colors function in image.h performs a normalized multiplication in each of the red, green, and blue channels.)
The result is an image that looks like the original but colors the “empty space” according to the illumination at that point.
Some Useful Functions
Please look through raycaster_util.h and image.h for many functions you can use to implement your algorithm.
Here are some particularly important ones, most of which we have already alluded to above:
Color illuminate(Light light, int x, int y)calculates our equation for illumination for a single point at a single non-occluded point.int is_obstacle(Color color)decides whether a given pixel is a solid obstacle.Pair direction_pair(PixelLocation start, PixelLocation end)finds the direction (angle) between two points.PixelLocation step(Pair* pos, Pair direction)moves a pixel position by one pixel in the given direction, which is useful for tracing the line segment representing each light ray. The in/out parameterposis a floating-point position that can represent fractional coordinates; it is mutated to reflect the new location. See the documentation comment inraycaster_util.hfor more details.Color add_colors(Color color1, Color color2)adds two color values together, for combining the effects of multiple lights.Color mul_colors(Color color1, Color color2)multiplies two colors, for applying the illumination color to the original pixel.Image* new_image(int width, int height)allocates a new, empty image. Use this to create the output image for all your raycaster implementations.Color* image_pixel(Image* image, int x, int y)gets a pointer to one pixel in an image at the given coordinates. This is just a one-liner that does the row-major index math (which some might prefer to write themselves).
Running and Testing
For a quick-and-dirty smoke test, use main.c.
This program uses a hard-coded input image and light arrangement;
you should experiment with different images and lights by manually modifying main.c.
Use rv make raycaster to produce the raycaster executable.
Running this executable produces raycast.png, which you can open in any image viewer.
We have also provided a more systematic testing framework in test_raycaster.c.
Use rv make test_raycaster to build a test_raycaster executable.
This tool uses inputs from your images/ directory and compares the results against reference outputs in images/test_references/.
It also saves the actual output images from your raycaster in images/sequential_results/ so you can inspect them visually if you like.
Expand the Test Suite
You must add at least 5 new tests to the test suite in test_raycaster.c.
For the sequential implementation, this means adding new input image files (scenes) and corresponding lines in test_raycast_sequential, possibly with different light positions.
Here are some ideas for kinds of tests you might add:
- Very small images that act as “unit tests” for specific edge cases.
- Different light positions for the existing images in the
images/directory. - New input scenes that you draw yourself using an image editor.
Make sure your implementation passes the given tests and your own new tests. It is important to be confident that your sequential implementation is correct before moving on to the parallel versions.
If you add new image files to go with your tests, you can optionally turn these in alongside your test code.
Task 2: Light-Parallel Raycast Implementation
In this and the next task, you will implement parallel versions of the raycaster. The first strategy uses parallelism over the light sources. The insight is that it is possible to independently compute the illumination due to each light. So we can use multiple threads to process subsets of the lights. The threads will then need to somehow coordinate to combine the contributions from separate lights and to produce the final image.
Complete this function in raycaster.c:
Image* raycast_parallel_lights(Image* scene, Light* lights, int light_count, int max_threads);
Your implementation may use up to max_threads parallel threads.
If there are fewer lights than max_threads, then you can use light_count threads (with one light per thread).
If there are more lights than max_threads, then each thread will have to process more than one light.
Use the pthreads library for all your thread creation, management, and synchronization needs.
The exact strategy for how to distribute work among threads and when to synchronize is up to you.
But be sure to unsynchronized accesses to shared data:
if two different threads might write the same variable, for example, use some pthreads synchronization construct to enforce exclusive access.
Test your implementation with test_raycaster.c.
Your parallel implementation should produce the same results as your sequential implementation.
Task 3: Row-Parallel Raycast Implementation
Next, we will use a different strategy to parallelize the same work. The idea is to parallelize the computation for different parts of the image. Namely, we will divide the rows (y-coordinates) of pixels among threads.
Implement this function in raycaster.c:
Image* raycast_parallel_rows(Image* scene, Light* lights, int light_count, int max_threads);
Again, the max_threads parameter describes how many threads your implementation can use.
You must divide the image’s rows among max_threads threads (unless the height is less than max_threads, in which case you will have one thread per row).
And once again, test your work using test_raycaster.c to ensure that your new implementation matches your sequential implementation.
Task 4: Performance Analysis
Your final task is to measure and compare the performance of your three implementations. There are many factors that can influence which raycaster implementation is fastest:
- The size of the image.
- The number of lights.
- The fraction of pixels containing solid obstacles.
- The number of threads. (Of course, only the parallel implementations support more than one thread.)
Conduct performance measurements to understand how your implementations’ running time changes as these parameters vary. For each of these four parameters, select at least 3 different values: 3 different images of different sizes, 3 light counts, 3 images with different obstacle densities, and 3 thread counts. Now, compare the running time of your three implementations on each of these different values. For each parameter, produce a single overlapping plot comparing the 3 implementations over your different values. You will have a total of four plots.
Write a short report consisting of these sections:
- Implementation: A brief summary of your implementation strategies for the three styles.
- Experimental setup: What parameters did you choose, and why?
- Results: Four plots examining the impact of the four parameters outlined above. (And any other data collect that you think is helpful.)
- Analysis: Attempt to explain what the results mean and why they look the way they do.
Submit your report as a PDF named raycast_writeup.pdf.
There is no minimum length, but please keep it to 3 pages or fewer.
Collecting Timing Data
If you add it up, the requirements above ask for a total of at least 33 data points:
- 27 total for the first three parameters (3 per implementation, per parameter)
- 6 total for varying the thread count (because only the 2 parallel implementations support more than one thread).
So it will be a good use of your time to partially or completely automate the data collection process. The strategy is up to you.
To help you get started, we have provided a basic data-collection program timing.c that you can adapt to your needs.
Modify this as much as you like; you will not turn it in.
You can start by changing the constants at the top of the file:
FILENAME (the input image),
LIGHT_NUMBER (the program generates lights in a grid pattern),
ITERATIONS (how many times to repeat the raycasting execution to measure an average execution time), and
THREAD_COUNT.
The current program only measures one parameter configuration at a time; you might consider extending it to try multiple configurations in a single run.
Use rv make timing to build the timing executable from timing.c.
Submission
On Gradescope, submit raycaster.c, test_raycaster.c (with your 5 additional tests), and raycast_writeup.pdf.
Rubric
- Implementation: 60 points
raycast_sequential: 20raycast_parallel_lights: 20raycast_parallel_rows: 20
- Performance Analysis: 20 points
- Additional Tests: 10 points