Minifloat
Instructions:
Remember, all assignments in CS 3410 are individual.
You must submit work that is 100% your own.
Remember to ask for help from the CS 3410 staff in office hours or on Ed!
If you discuss the assignment with anyone else, be careful not to share your actual work, and include an acknowledgment of the discussion in a collaboration.txt file along with your submission.
The assignment is due via Gradescope at 11:59pm on the due date indicated on the schedule.
Submission Requirements
For this assignment, you will need to submit the following five files:
minifloat.c, with your written implementation for the missing functions.minifloat_test_part1.expected, to match additional tests added inminifloat_test_part1.c- Some additional tests, in:
minifloat_test_part1.cminifloat_test_part2.cminifloat_test_part3.c
Restrictions
For this assignment, you will be working with building your own floating-point representation.
- You may not use built-in C operations for floating-point arithmetic.
- You may not cast data to
floatordouble, or create variables with these types.
Provided Files
The provided release code contains seven files:
minifloat.c, which includes some completed functions and some functions you are expected to implementminifloat.h, which provides declarations and comments for the functions inminifloat.c, including those you are to implementminifloat_test_part1.c,minifloat_test_part2.c,minifloat_test_part3.c, which provide some tests for you to get started. You are expected to add more tests of your own to each of these test suitesminifloat_test_part1.expected, which provides a baseline file to help with testing part 1. You are expected to add more lines to this file as part of testing part 1.Makefile, which provides structure to compile your code (see our brief tutorial on Makefiles)
Getting Started
To get started, obtain the release code by cloning your assignment repository from GitHub:
$ git clone git@github.coecis.cornell.edu:cs3410-2024fa/<NETID>_minifloat.git
Replace <NETID> with your NetID. For example, if your NetID is zw669, then this clone statement would be git clone git@github.coecis.cornell.edu:cs3410-2024fa/zw669_minifloat.git
Overview
In this assignment, you will be developing a custom minifloat data format in C. You will be expected to reason about floating-point details and to implement C functions.
Background
In class, we learned about floating-point numbers, which represent decimals with some number of bits.
C has built-in float and double types, which use (on modern hardware)
32 bits and 64 bits, respectively.
Increasing the number of bits in a floating-point representation gives it more precision and more dynamic range, at the expense of less efficient arithmetic.
It can also be useful, however, to perform operations with smaller floating-point representations—trading off precision for potentially faster calculations.
In this assignment, you will implement functions for a specialized 8-bit floating-point type. We’ll call these 8-bit numbers minifloats. Minifloats have severely limited precision, but such tiny floating point values are useful for situations where errors matter less and data sizes are enormous: most prominently, in machine learning. See, for example, this paper and this other paper that both show serious efficiency advantages from using 8-bit minifloats. While most floating point formats enjoy built-in hardware support, we can also implement minifloats in software with bit packing tricks.
Minifloats follow a similar representation strategy to the standard IEEE floating-point types that we learned about in lecture. However, they differ in a few important ways to make the implementation simpler, which we will summarize as well.
Minifloat specification
- Minifloats use 8 bits in total: 1 sign bit, 3 exponent bits, and 4 significand bits. The layout of a minifloat looks like this, with
sfor sign,efor exponent, andgfor significand:
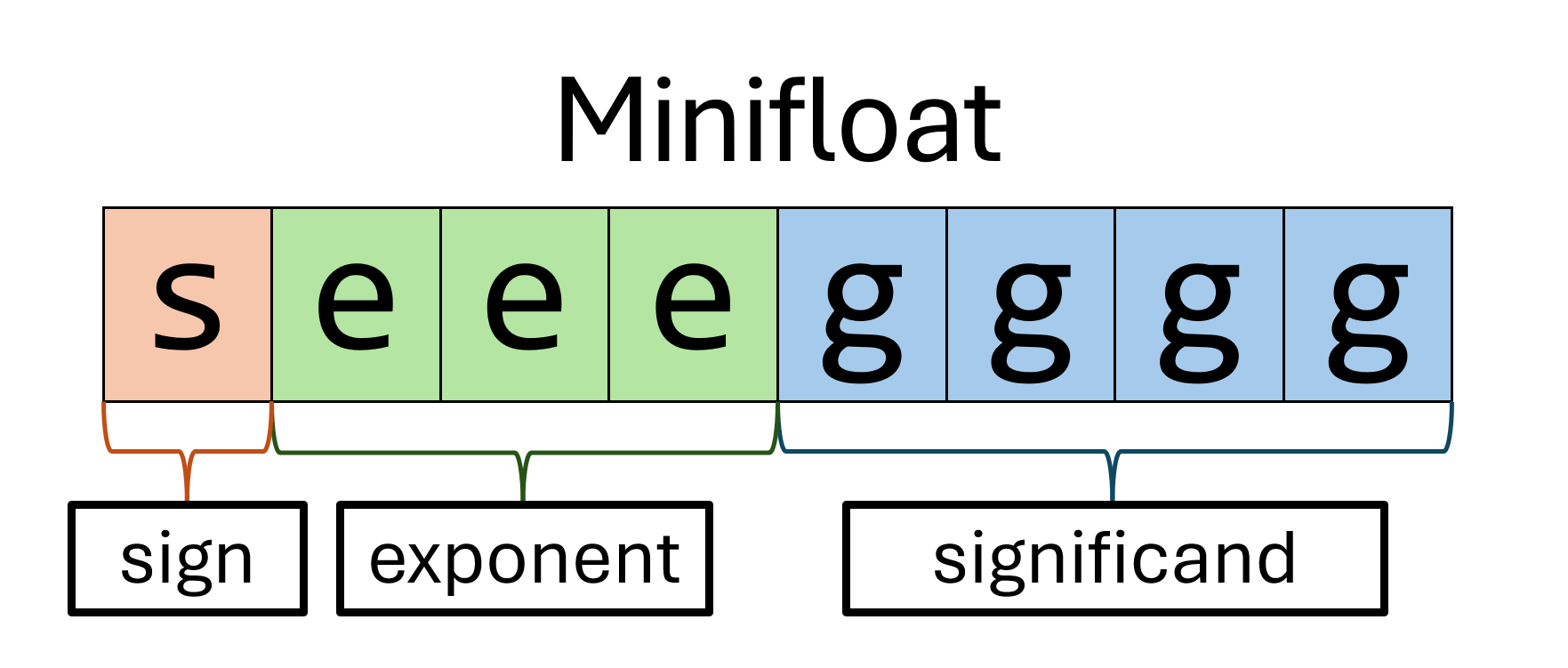
-
As in standard formats, a sign bit of
0indicates a positive number, and a sign bit of1indicates a negative number. -
Minifloats have a bias of 3. In other words, we subtract 3 from the bit-representation of a minifloat exponent.
-
Unlike standard floating-point formats, wherein we usually append a leading 1 to the significand bits with the 1.g notation, minifloats use the significand directly, with the binary point after the first digit. So if the four significand bits are g3g2g1g0, then the “base” part of the represented value is the binary number g3.g2g1g0. Or, in other words, the value is g×2−3, where g is the unsigned integer value of those 4 bits.
-
Also unlike standard floating-point formats, our minifloats do not use special values: not a number (NaN) and infinity (+∞ and -∞).
All together, the value represented by a minifloat with sign s, exponent e, and significand g is:
(−1)s×(g×2−3)×2e−3
Or, equivalently, if you prefer to think of the significand’s representation in terms of bits:
(−1)s×(g3.g2g1g0)×2e−3
where g3 is the significand’s most significant bit, g0 is the least significant bit, and so on.
Minifloat Examples
To help with reading a minifloat, here are a pair of example calculations of reading a minifloat as a base-10 decimal:
Example 1: 10111100
We have a sign of 1, an exponent of 011, and a significand of 1100.
- Our sign
1corresponds to −1. - Our exponent
011corresponds to a decimal exponent of 3−3=0. (We’re applying our −3 bias here.) - Our significand
1100corresponds to the decimal 12×2−3=128=1.5. (Or, equivalently, the significand corresponds to the binary number 1.1002, which is 1.5 in decimal.)
In total, our number is then −1×1.5×20=−1×1.5×1=−1.5.
Example 2: 00010010
We have a sign of 0, an exponent of 001, and a significand of 0010.
- Our sign
0corresponds to +1. - Our exponent
001corresponds to a decimal exponent of 1−3=−2. - Our significand
0010corresponds indicates the binary value 0.0102, which equals 0.2510.
In total, our number is then 1×0.25×2−2=116=0.0625.
Bit size in C
We want to ensure that the type we are using to represent a minifloat is exactly 8 bits.
We will use the uint8_t type from C’s stdint.h header.
(We will avoid char, even though char is 8 bits on most platforms, because C unhelpfully does not guarantee that is is exactly 8 bits everywhere.)
To break down this type’s, the uint means that bit-level operations are as on an unsigned integer, the 8 means that we expect operations to be on 8 bits, and _t is a common naming convention that indicates that this is a type.
The stdint.h header defines many similar types, like these:
| Type | Description |
|---|---|
| uint8_t | unsigned integer with 8 bits |
| uint16_t | unsigned integer with 16 bits |
| int8_t | signed integer with 8 bits |
Your Task
This assignment is divided into three parts: displaying minifloats as decimals, implementing operations on minifloats, and using minifloats. Each part will have you implementing 1–3 functions, and adding test cases to help convince yourself these functions are correct. You must add at least 4 new test cases per function to what we have provided, though you may add more.
For all of your C implementations, you may not include any constants or variables of type float, double, or long double.
You may not use C’s built-in floating-point operations, such as + on floating-point values.
This is not an arbitrary restriction. Using a larger float representation in your implementation will defeat the purpose of the smaller representation, which is that they are smaller and faster than “normal” floating-point types. Because of floating-point error, it is also very likely to introduce incorrect results.
We have provided a mini_to_double utility function to help you with debugging and testing. You may not use this function in any of your submitted implementations, but you may use this function for writing test cases for any of your functions.
Part 0: Lab
View the lab slides here.
In this lab, you will gain practice using floating point numbers. There are 2 designated checkoff points where you should show your work to a TA.
Review
If you need to, look over the lecture notes on standard floating-point types to remind yourself of the basic principles. And try out float.exposed to get hands-on practice!
Read over the background above and especially the specification for minifloats. To briefly summarize the minifloat format:
- Bit 7 is the sign bit
- Bits 6–4 are the exponent bits
- Bits 3–0 are the fraction bits
(Bits are numbered from the right, so 0 is the least significant bit.)
Part 0.1: Practice Conversions
Decimal to float. To convert from a decimal to a floating point number:
- Convert the integer and fractional parts into binary.
- Combine the results and shift accordingly.
- Convert our exponent into biased form.
- Convert the fractional part into a mantissa/significand.
- Recombine for a final floating-point representation.
Here’s a 32-bit example. Consider the decimal 12.375.
Converting the integer portion into binary yields 1100.
Converting the fractional part is a little more labor intensive. Our fractional part is 0.375. To convert, multiply the fractional part by 2, record the integer part of the result (should be 0 or 1), and repeat with the new fractional part until the fractional part becomes 0 or the precision limit is reached (is 23 digits for the IEEE 754 32-bit format). The recorded integer parts of this process becomes our binary representation for the original fractional part.
- 0.375×2=0.750. Record
0. - 0.750×2=1.500. Record
1. - 0.500×2=1.000. Record
1.
Thus our binary representation of 0.375 is 011, and thus our binary
representation of 12.375 is 1100.011.
We now normalize our result so that it fits the format (1.xyz…)×2e. In this case, we shift to the right to obtain 1.100011×23.
Next, we need to apply our format’s exponent bias, which for this format is 127. To bias the exponent, we add our original exponent with the bias. In our example, this gives us 3 + 127 = 130.
From here, we can see that:
- The biased exponent form of 130 yields
10000010in binary. - The fractional part is 1000112, and thus our mantissa is
10001100000000000000000. (We fill in the remaining digits with 0s.) - We have a positive number, so our sign bit is
0.
(The reason the exponent’s “bias” of 127 exists is so that we can represent both positive and negative exponents using an unsigned integer. It may help to think of the bias as the reference point of no shifting (an exponent of 0), and any additions and subtractions to this bias represent how much we shift by. To find the to find the bias of any floating-point number, we can use the formula 2(k−1)−1 where k is the number of bits in the exponent field.)
Thus, our final floating point representation is 0 10000010 10001100000000000000000.
You can try checking the answer by entering these bits into float.exposed if you like.
Float to decimal. To convert from a floating-point number to a decimal number:
- Separate out the sign, exponent, and mantissa.
- We restore the 1. back to the mantissa and drop the trailing 0s.
- We de-normalize the number so the exponent is 0.
- Convert the integer and fractional parts to decimals.
- Add a negative sign if necessary.
Exercises:
- Convert -4.75 to our 8-bit floating point format.
- Convert 1.7 to our 8-bit floating point format.
- Convert the binary float 11010011 to a decimal.
- Convert the binary float 00100110 to a decimal.
Checkoff #1: Show your converted numbers to a TA.
Part 0.2: Floating Point Addition and Inaccuracies
You can perform many arithmetic operations with floating-point numbers. However, in this lab, you will be practicing with addition as an introduction to floating-point arithmetic.
To perform addition with a floating point number:
- Rewrite the smaller number so that the exponents are equal, and adjust the mantissa of the number with the smaller exponent by shifting it to the right accordingly.
- Add the mantissas together.
- Recombine and renormalize the result if necessary.
Exercises:
- Add 0.25 and 8.0 with our 8-bit minifloat format.
- Add 1.25 and 2.5 with our 8-bit minifloat format.
- Can you find two numbers that share the same nearest minifloat representation?
- What is the largest number our minifloat format can represent?
Take note of where accuracy was lost in these calculations. Why are our results so far off from what we expect?
Checkoff #2: Show your addition results to a TA.
Part 1: Displaying Minifloats
Your first task is to implement a function for displaying minifloats in C, named print_mini. This function takes in a minifloat and must print the sign, whole number, and fractional part associated with this minifloat as a base-10 value. The exact specification, with examples, is given in minifloat.h. Your implementation should be filled into minifloat.c.
To make your task somewhat easier, we have written a concrete call to printf at the end of the each function that you may use as a guide for what to implement. Note that print_mini requires that we write 6 decimal digits—the provided printf specifier %06d will fill any integer to have preceding zeros such that the printed integer has 6 digits. To provide two concrete examples:
printf("%06d", 123)will print000123printf("%06d", 100000)will print100000
Remember, you may not include any constants or variables of type float, double, or long double, and you may not use any floating-point operations.
You may, however, use any integer arithmetic operation (including integer division and modulus).
In C, dividing two integers with i / j produces an integer.
But be sure not to include a double constant (such as 1.0) by accident.
Hint: You may find it useful to observe that 1/64=0.015625, and that, with integer division, 1000000/64=15625.
Testing Part 1
A test script to help guide your development can be found in minifloat_test_part1.c. You can build this test with the following command:
rv make part1
To test this code, you must execute the resulting .out file and pipe your print results to a file, such as with the following command:
rv qemu minifloat_test_part1.out > minifloat_test_part1.txt
Reminder: use the rv aliases for each command if you have it set up!
Finally, you must compare the resulting prints to our expected results using diff:
diff minifloat_test_part1.txt minifloat_test_part1.expected
If you observe any differences between the two, a printing test failed.
You can also combine these operations into a single bash command:
rv make part1 && rv qemu minifloat_test_part1.out > minifloat_test_part1.txt && diff minifloat_test_part1.txt minifloat_test_part1.expected
Reminder: You must add 4 new printing tests (which means modifying both minifloat_test_part1.c and minifloat_test_part1.expected).
Part 2: Minifloat Operations
Your second task is to implement an equality check, addition, and multiplication between minifloats. Specifically, you will be implementing mini_eq, mini_add, and mini_mul, which both take in two minifloats and produce a new minifloat. As before, the specifications for each function can be found in minifloat.h, and your implementation should be written in minifloat.c.
The results of the arithmetic operations mini_add and mini_mul must produce the minifloat value closest to adding together the corresponding real numbers. If there are two possible closest real numbers, your implementation must correspond to the closest real number further from zero than the result of addition. For example, we would round 2.125 to 2.25, and similarly -1.0625 to -1.125.
If there are multiple possible minifloat representations of the resulting real number, you must return the minifloat with the smallest exponent. For example, the minifloat value 0 011 0010 could be equivalently represented as 0 001 1000, and only the latter is considered correct for these arithmetic operations. Additionally, if an arithmetic operation would return 0, you must return exactly 00000000.
If applying addition or multiplication would result in a real number larger or smaller than can be represented by a minifloat, the result of these operations is undefined, and need not be tested.
Hint: If you become stuck on any of these functions, consider attempting another—each requires detail that can become more obvious while working on another.
Testing Part 2
Testing minifloat operations is more straightforward than testing the printing implemented earlier. We can simply run each test file and compare the resulting minifloats to expected values. To test part 2, you can directly build and execute part2:
rv make part2 && rv qemu minifloat_test_part2.out
Reminder: You must add 4 new tests per function.
Hint: Write as many edge-case tests as you can think of, there are many potential tricks with negative numbers and very small or very large minifloats.
Part 3: Using Minifloats
Your third task is a straightforward example use of the minifloats you have implemented. Specifically, you’ll be implementing functions to calculate the volume and surface area of a cylinder in the functions titled cylinder_volume and cylinder_area.
The volume and surface area of a cylinder depends on two variables, the radius r and height h of the cylinder, by the following equations:
- volume=π×r×r×h
- surface area=2×π×r×(h+r)
For reference and comparison, we have also written an implementation of these functions double_cylinder_volume and double_cylinder_area. These may be useful to refer to while implementing your own function, but are also used for the written task below.
For these implementations, you are expected to use the constant minifloat representation of PI to be 01001101 (representing 3.25), which is the closest minifloat to the decimal π≈3.14159. We have included this constant definition in minifloat.c for your convenience.
Testing Part 3
To test part 3, you can directly build and execute part3:
rv make part3 && rv qemu minifloat_test_part3.out
We have only provided you with a single simple test for each, and you should write at least 4 new tests. We test these particular functions by comparing our minifloat calculation to the result produced by calculating the same value with a double. We expect that the minifloat result (being less accurate) will have some error compared to the double representation, which in the test is represented by the threshold parameter.
We recommend trying out a few operations and seeing how difference there is between minifloat and double calculations, and adjusting your threshold accordingly. To help with comparing these operations, we use the provided mini_to_double utility function to calculate calculate a double value before and after computing the minifloat equivalent.
(We do not define a double_to_mini conversion.)
The mini_to_double utility is only for testing.
Do not use it in your main implementation.
Remember that your goal is to implement minifloat operations “from scratch,” using only integer arithmetic.
This is what makes minifloats more efficient than float or double.
Your tests should not include cases where the minifloat arithmetic would overflow (produce a result larger than the maximum minifloat or smaller than the largest negative minifloat). We do not define the results of these overflowing operations.
Submission
Submit minifloat.c, minifloat_test_part1.expected, minifloat_test_part1.c, minifloat_test_part2.c, and minifloat_test_part3.c to Gradescope.
Upon submission, we will provide a sanity check to ensure your code compiles and passes the public test cases.
Rubric
- 16 points:
print_minicorrectness - 18 points:
mini_eqcorrectness - 16 points:
mini_addcorrectness - 19 points:
mini_mulcorrectness - 8 points:
cylinder_areacorrectness - 8 points:
cylinder_volumecorrectness - 15 points: test quality