Cache Optimization

Instructions: Remember, all assignments in CS 3410 are individual. You must submit work that is 100% your own. Remember to ask for help from the CS 3410 staff in office hours or on Ed! If you discuss the assignment with anyone else, be careful not to share your actual work, and include an acknowledgment of the discussion in a collaboration.txt file along with your submission.

The assignment is due via Gradescope at 11:59pm on the due date indicated on the schedule.

Overview

In this assignment, you will explore the effects on performance of writing “cache-friendly” code, i.e., code that exhibits good spatial and temporal locality. The focus will be on implementing matrix multiplication.

Release Code

You are provided with these files:

• tasks.c, tasks.h: The matrix multiply functions you will implement. All your programming work happens in tasks.c. Do not modify tasks.h.
• matmult.c: A command-line program (i.e., a main function) to run (and time) the matrix multiplication functions.
• helpers.c, helpers.h: A few utilities for the user interface and allocation.
• Makefile: A recipe for building and running your code. The Makefile includes a few options to help adjust parameters for your code; we’ll introduce those below.
• test_matmult.c: Some tests for the matrix multiply functions. Type make test to build the tests.
• collect_times.py and plot_times.py: Scripts to collect and visualize execution times for the matrix multiplication functions.
• transpose.c, test_transpose.c: Implementation and tests for some matrix transpose functions. You don’t need these to complete your work, but you can use them to try out some examples of matrix-processing functions.

You will only modify tasks.c. Do not modify any other source-code files. You will also turn in a discussion.txt file (not provided).

Background: Optimizing for Locality

The performance penalty of a cache miss can be significant, and thus the performance improvement that cache memory offers is greatest when the data we need to operate on remains in the cache for as long as we need it. In the big picture, we want to write code that has good spatial locality: when a data location is referenced, the program will reference nearby locations soon.

There are a variety of techniques to improve the spatial locality of a program and to exploit good spatial locality for improving performance. In this project, you will explore some of these techniques in the context of matrix multiplication, a simple algorithm with a wide variety of real-world applications.

Representing Matrices

To implement matrix multiplication, we need a way to represent these matrices as arrays. In other words, say we have a matrix with \(m\) rows and \(n\) columns, so \(m \times n\) total elements. We want to represent this as a C array of length \(m \times n\). We therefore need to decide which order to put the elements in. There are two basic options:

• Row major: Element \(M_{ij}\) (i.e., M[i][j]) is at M[i*n + j] in the array.
• Column major: Element \(M_{ij}\) (i.e., M[i][j]) is at M[i + j*m].

In row-major order, you can visualize all the rows concatenated together, one row at a time. In column-major order, instead visualize the columns being laid out one at a time into the flattened array.

Many programming languages (including C!) have multi-dimensional arrays. Of course, they have to implement them somehow—typically, they pick one of these two styles. In C, multi-dimensional arrays use a row-major order.

The choice of layout can have profound implications for the locality of algorithms that access the matrix.

Matrix Multiplication Refresher

In linear algebra, matrix multiplication is a binary operation on two matrices, A and B. In the product \(C = AB\), each element \(c_{ij} \in C\) is equal to the dot product of row \(a_{i\star}\) and column \(b_{\star j}\). For example, for the \(n \times n\) matrices A and B:

\[ \begin{array}{rclrcl} A & = & \left( \begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array} \right), & B & = & \left( \begin{array}{ccc} 11 & 12 & 13 \\ 14 & 15 & 16 \\ 17 & 18 & 19 \end{array} \right) \end{array} \]

we have the product:

\[ \begin{array}{rcl} C & = & \left( \begin{array}{ccc} 90 & 216 & 342 \\ 96 & 231 & 366 \\ 102 & 246 & 390 \end{array} \right) \end{array} \]

Here is some pseudocode for a function that multiplies two square N-by-N matrices:

void matmult(double A[][], double B[][], double C[][]) {
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < N; j++) {
            double cij = 0.0;
            for (int k = 0; k < N; k++) {
                cij += A[i][k] * B[k][j];
            }
            C[i][j] = cij;
        }
    }
}

This version loops over all the cells in the output matrix, C, and calculates them one at a time. To compute the C entry, we access the corresponding row of A and the corresponding column of B. The innermost loop accumulates the dot product of this row and column.

While this pseudocode uses two-dimensional access expressions like A[i][j], your real code for this assignment will need to exercise direct control over the memory layout. So the matrices will be ordinary, 1-dimensional arrays, and you’ll access them by calculating the appropriate indices manually, like A[i*N + j].

Access Patterns in Matrix Multiplication

Let’s think about the memory accesses in this function, assuming a row-major layout. Consider the contents of an \(8 \times 8\) product matrix C, at the point when we have just calculated the value for \(c_{22}\):

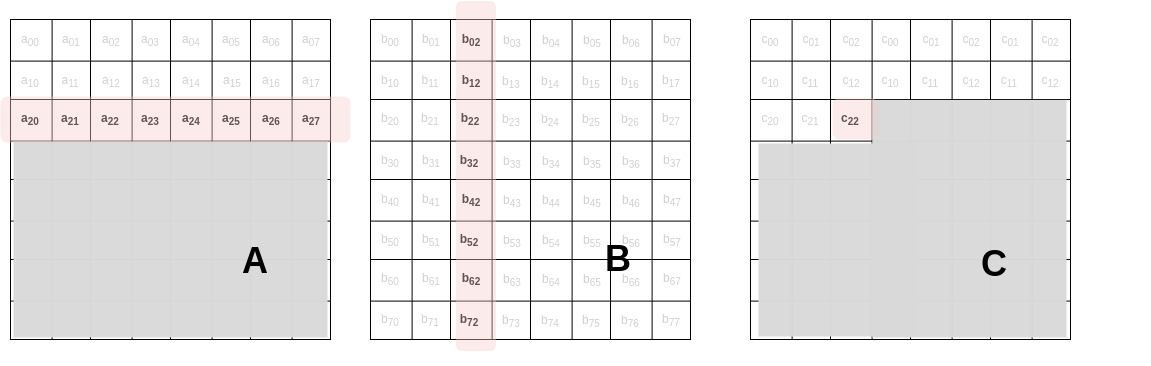
The innermost loop of the algorithm will load the entire highlighted row of A and column of B. Here’s what that loop looks like if we use a row-major order:

for (int k = 0; k < N; k++) {
    cij += A[i*N + k] * B[k*N + j];
}

Think about the way the two array access expressions, A[i*N + k] and B[k*N + j], “move” across the iterations of this loop, as we increment k. The access to A “moves” by 1 element at a time (8 bytes, because we’re using doubles). The access to B, on the other hand, moves by N elements each time. We can visualize these accesses in the 1-dimensional realm of memory addresses:

Performance engineers would say that these accesses are strided. The A access has a stride of 1 element (8 bytes), and the B access has a stride of N elements (or N*8 bytes).

Which stride seems like it’s probably better for spatial locality? In other words, which access will have a higher hit rate in the processor’s data cache?

Cache Blocking

Blocking or tiling is a strategy for improving the locality of loop-based algorithms. It’s effective when the data you’re processing (e.g., matrices) are so large that they cannot fit entirely into the processor’s cache. The basic idea is to break the problem into smaller blocks that do fit the cache and process them one at a time.

General Strategy

Here’s the general strategy for blocking an algorithm. If your original program consists of d nested loops, then add d more loops at the innermost level. These new loops will process one fixed-size block. Generally, we’ll process the block as if it were a smaller version of the original problem (e.g., a multiplication of two small, block-sized matrices). Then, the original (outer) loops will iterate over all the blocks in the big data structure.

Here’s a 1-dimensional example. Let A be an array with N elements. If the original algorithm is:

for i in 0..N:
    do_stuff(A[i])

Let’s add blocking, with block size B. Assuming B is a factor of N for simplicity, there are exactly N/B blocks in N. So the blocked version would be:

num_blocks = N/B
for block in 0..num_blocks:
    for i in (block * B)..((block + 1) * B):
        do_stuff(A[i])

The pattern generalizes to two dimensions (i.e., matrices). Just like the matrices themselves, the blocks will also be 2-dimensional. If our algorithm starts like this (assuming square N-by-N matrices):

for i in 0..N:
    for j in 0..N:
        do_stuff(A[i][j])

The blocked version, with B-by-B blocks (again assuming B evenly divides N), becomes:

num_blocks = N/B
for ii in 0..num_blocks:  # iterate over row blocks
    for jj in 0..num_blocks:  # iterate over column blocks
        for i in (ii * B)..((ii+1) * B):  # rows within the block
            for j in (jj * B)..((jj + 1) * B):  # columns within the block
                do_stuff(A[i][j])

If you want to support the case where B does not perfectly divide N, you will want to use something like min(N, (ii+1) * B) to make sure the inner loops don’t run off the end of the array.

An Example: Matrix Transpose

Consider this implementation of the transpose operation on an \(n \times n\) matrix, which exchanges the rows and columns:

// Calculate the transpose of M, storing the result in M_t. Both are
// stored in row-major order.
void transpose(int n, double* M, double* M_t) {
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
             M_t[j*n + i] = M[i*n + j];  // M_t[j][i] = M[i][j]
        }
    }
}

Let’s apply the blocking principle to this loop nest:

void transpose_blocked(int n, double* M, double* M_t) {
    int num_blocks = n/BLOCKSZ;  // # of block rows & block columns

    for (int ii = 0; ii < num_blocks; ii++) {  // for every row block
        for (int jj = 0; jj < num_blocks; jj++) {  // every column block
            for (int i = ii*BLOCKSZ; i < (ii+1)*BLOCKSZ; i++) {
                for (int j = jj*BLOCKSZ; j < (jj+1)*BLOCKSZ; j++) {
                    M_t[j*n+i] = M[i*n + j];
                }
            }
        }
    }
}

Think about the access patterns in this blocked version. The matrices themselves consist of N*N*8 bytes; the blocks are B*B*8 bytes. If the blocks fit in a system’s cache, but the whole matrices do not, what will the effect on the hit rate be?

We have provided a complete implementation in helpers.c. Let’s try it out! Type these commands:

rv make transpose BLOCK=<block size>
rv qemu transpose <matrix size>

We’ve set things up so you provide the block size at compile time and the matrix size at run time. So you can compile the program with a fixed block size and try it with many different matrix sizes. We’ve done this because using a fixed block size lets the compiler do a lot more optimization than it could if the block size were a run-time parameter.

For example, try a block size of 8 and a matrix size of 2048 to start with. (Now would be a good time to ask: How many bytes in a block? How many bytes in these matrices? What is likely to fit in your processor’s cache?)

The program reports the running time for a naive version, a blocked version, and a version with a loop interchange optimization (more on this next). The blocked version, even though there’s a lot more code, should be faster—although the details depend on your computer. When I ran with these parameters, for example, the naive version took 47 ms and the blocked version took 21 ms. Locality matters!

Loop Interchange

Loop interchange is a fancy term for a simple idea: switching the “nesting order” of a loop nest. For some algorithms, just performing this interchange can have a large effect on access patterns and therefore on cache performance.

In general, if you have a loop like this:

for i in 0..m:
    for j in 0..n:
        do_something(i, j)

Then interchanging the i and j loops would just mean making the j loop the outermost one:

for j in 0..n:
    for i in 0..m:
        do_something(i, j)

Loop interchange is only correct for some algorithms. It would not be safe to perform, for example, if do_something(i, j) just printed out the values of i and j; interchanging the loops would change the output of the program.

The transpose function above, however, is an example where loop interchange is correct, because every iteration of the innermost loop writes to a different location in the output matrix. Here’s a version with the i and j loops interchanged:

void transpose_interchanged(int n, double* M, double* M_t) {
    for (int j = 0; j < n; j++) {
        for (int i = 0; i < n; i++) {
            M_t[j*n+i] = M[i*n + j];
        }
    }
}

Will this version be faster or slower than the original? Think about the access patterns for the M and M_t accesses in the innermost loop body.

In the original function, the read of M had a stride of 1 element and the write to M_t had a stride of j elements. In the interchanged version, the strides are reversed. So this version should be no better or worse than the original. As we will see in this assignment, however, loop interchange can have a real effect on other algorithms.

Task 0a: Basic Row-Major Matrix Multiply

To warm up, you will first implement, test, and measure some basic implementation of matrix multiplication. First, implement a row-major matrix multiply in the function matmult in tasks.c.

The function signature looks like this:

void matmult(int n, double* A, double* B, double* C);

The first parameter, n, gives the size of the matrices. (We will only deal with square matrices in this assignment, so A, B, and C are all n-by-n matrices.) A and B are both inputs, and C is the output matrix.

To implement this function, you can follow the pseudocode for matrix multiplication above. You will need to implement the 2D matrix notation, like A[i][j], with the appropriate index calculations to access the appropriate array entry in row-major order.

Test It

Test your implementation by building and running the provided test_matmult.c. Try these commands:

$ rv make test_matmult
$ rv qemu test_matmult <size>

Use a matrix size of 2 to begin with, and then try (slightly) larger matrix sizes. Our test program runs all the implementations of matrix multiplication in this assignment, but those should all just output zeroes for now. Pay attention only to the first chunk of output for now, which shows the inputs and your matmult’s output. Use any method you like to confirm that the output matrix is correct: for example, you could use NumPy’s matmul function.

Measure It

We have also provided code to measure the performance of your matrix multiplication implementations. Build and run the matmult.c program:

$ rv make matmult
$ rv qemu matmult <size>

Start with a matrix size of 256 or 512 for this performance measurement. The program reports the running time (in milliseconds) for every matrix multiply implementation in this assignment; because you haven’t implemented the later ones yet, those should all take 0 ms. Try a few different sizes to get a sense for how your \(O(n^3)\) algorithm performs.

Task 0b: Column-Major B Matrix

Next, we’ll implement a variation on the basic algorithm where the B matrix (and only the B matrix) is stored in column-major instead of row-major order. The other two matrices, A and C, will remain in row-major order. Our code reformats B for you, so you don’t have to do anything to get it into column-major format—just assume that it comes to you that way.

Implement this version in the matmult_cm function. You can even copy and paste your matmult function body to get started, and then make any changes necessary to access B in column-major style.

Test your implementation with test_matmult. The version “with column-major realignment” should match your original implementation’s result. Try a few different matrix sizes to confirm that it does.

Measure your implementation with matmult. Compare the running time for the “naive” and “realigned” versions for a few different (larger) matrix sizes.

Finally, write your answers to the following question in discussion.txt, labeled Discussion 0b. Which is faster: the original “naive” version or your “realigned” matmult_cm? Try to identify any trend that is consistent across matrix sizes. Write 1–2 sentences to explain the difference.

Task 0c: Loop Interchange

Apply the loop interchange optimization to your original (all row-major) matrix multiply. Specifically, interchange the j and k loops. The order of iteration will therefore be:

• Outermost loop: i, the row in C.
• Middle loop: k, the column of A and row of B.
• Innermost loop: j, the column in C.

Just swapping the order of the loops will not work. There is more to this task to make sure the matrix multiplication is still correct. Specifically, if you start with the matrix multiply pseudocode and make j the innermost loop, the variable j won’t even be in scope for the access to C[i][j]!

The general strategy here is to skip the accumulation into a local variable cij and instead add directly to the output entry (C[i][j] in the pseudocode). You may assume that C is initialized to hold all 0.0 values as a precondition, so it is safe to accumulate into C without first initializing it yourself.

Put your implementation in the matmult_li function. Once you have something working, determine the access patterns for the array accesses inside the innermost loop. How do they differ from the original version? Using your analysis of the access patterns, make (and write down) a hypothesis about which version will be faster.

Test your implementation to make sure the output matches your first implementation. (Build and run test_matmult.c to compare all the outputs on a few different sizes.) Then, measure your performance to check your hypothesis about this version’s performance. (Build and run matmult.c.)

Finally, answer these questions in discussion.txt. Label your answers with Discussion 0c. You only need 1–2 sentences per question:

1. Describe the access patterns for the matmult_li function. Characterize the stride length of each array access expression.
2. How do these access patterns differ from the original matmult implementation?
3. What was your hypothesis about which version was likely to be faster?
4. Was your hypothesis correct? Describe the measurements you used to decide.

Task 1: Blocking

The final version of matrix multiplication that you will implement is blocking, a.k.a. tiling. Your blocked matrix multiply will go in the matmult_bl function in tasks.c.

In helpers.h, we have defined a BLOCKSZ macro. Use this for the size of the blocks (tiles) that you process: i.e., you will multiply BLOCKSZ-by-BLOCKSZ square chunks of the matrices, one at a time. (As we outline in the background section, making this value a compile-time constant, instead of a parameter to the function, lets the compiler do important optimizations.)

Because we’re again assuming row-major order, you can start by copying and pasting your implementation for the basic matmult. Following the recipe from the background section, you’ll need to do these things:

• Calculate how many blocks you need in each dimension. If the matrices have a size of n in each dimension and your blocks have size BLOCKSZ in each dimension, how many blocks do you need in a given dimension? Be sure to consider the case where BLOCKSZ does not evenly divide n.
• Duplicate the 3 loops, for a total of 6 nested loops. The outer 3 will iterate over the blocks in the matrix, and the inner 3 will iterate over the elements within a single block.

You will also need to reuse one insight from your loop interchanged version. Instead of accumulating into a local variable like cij in the original pseudocode, you will want accumulate directly into the C matrix (relying on the precondition that it is initialized to zero). This approach yields a convenient way to combine the results of different blocks.

When your implementation is complete, the inner 3 loops should look a lot like a little “naive” matrix multiply of its own! Indeed, a blocked matrix multiply consists of a bunch of little multiplications of the sub-matrices formed by the blocks.

“Short Circuit” Instrumentation

To make it easier to test your code (and to make it possible for us to grade your blocked implementation), we will add an option to stop the execution after two blocks. You must add this line to your code:

if (check_shortcircuit()) return;

Put this line at the top of the innermost block loop, which should be before the start of the outermost element loop. In other words, your implementation should consist of 6 nested loops; put this at the top of the body of the 3rd loop, before the 4th loop starts. If you’d like an example, see transpose_bl in helpers.c.

The check_shortcircuit function is defined in helpers.c. Below, we will show you how to use this instrumentation to see the intermediate results for debugging purposes.

Test It

Because BLOCKSZ is a compile-time constant, testing is a little more complicated than for the other versions of our matrix-multiply function. Follow these steps:

$ rv make clean  # Delete the old version, which may use a different block size.
$ rv make test_matmult BLOCK=2  # Build with a new block size.
$ rv qemu test_matmult 4  # Run with a given matrix size.

Providing the BLOCK=<size> argument to make will define the BLOCKSZ macro in your code. Then, you can run the compiled code on different matrix sizes without rebuilding.

The “short circuit” option is also compile-time parameter. To enable it, pass SC=1 to the Makefile. Try this:

$ rv make clean
$ rv make test_matmult BLOCK=2 SC=1
$ rv qemu test_matmult 4

Look at the output for the “with blocking (shortcircuit)” version. Many of the entries will be zero. This is the “intermediate state” of the C matrix after finishing two blocks. You can use this option to debug your blocked implementation if it produces wrong answers.

Measure It

You also need the BLOCK=<size> argument to measure the performance. Do something like this:

$ rv make clean
$ rv make matmult BLOCK=4
$ rv qemu matmult 512

Task 2: The Optimal Block Size

Blocking is good for large matrices that do not fit in a processor’s cache. It is effective because it creates a smaller working set that can fit in the cache. The optimal choice of the BLOCKSZ parameter, therefore, depends on the size of your computer’s cache.

Let’s empirically measure the best block size on your machine. We have provided two Python scripts to help run an experiment: collect_times.py, to take measurements, and plot_times.py, to draw a graph of them.

First, we’ll measure how long matrix multiplication takes with various block sizes. Run a command like this:

$ python collect_times.py -n 128 -b 1,2,4,8,16,32,64,128

Use -n to specify the matrix sizes to try and -b for the block sizes. The script will try all combinations of the two lists. It produces a file runtimes.csv, which you can inspect manually or open in a spreadsheet app if you like.

The second script can plot this data as a line chart. It requires Matplotlib; you will need to install it with something like pip install matplotlib (but the details depend on your platform; see the installation manual if you need help). Then, just run:

$ python plot_times.py

The script displays the plot and produces an image in plot.png.

Collect and visualize some data to answer these questions. Write your answers in discussion.txt, labeled Discussion 2:

1. What is the best block size on your machine? (Is it consistent across different matrix sizes?)
2. Is there a block size beyond which performance seems to degrade? What does this tell you about the size of your computer’s caches?

Submission

There are two files to submit:

• tasks.c, containing your implementations of matmult, matmult_cm, matmult_li, and matmult_bl.
• discussion.txt, containing your three sets of answers to the discussion questions in Task 0b, Task 0c, and Task 2. Label your answers Discussion 0b, Discussion 0c, and Discussion 2.

We will run your code with our versions of the other source-code files, so do not modify any C code outside of tasks.c.

Rubric

• Implementation: 50 points
  • Basic row-major version: 5
  • Column-major operand version: 10
  • Loop interchange: 10
  • Blocked version: 25
• Discussion: 20 points
  • Discussion 0b: 5
  • Discussion 0c: 5
  • Discussion 2: 10