


Next: Functions
Up: Introduction
Previous: Architecture of type theory
Since Post it has been the accepted practice to define the class of formulas
and the notion of proof inductively. Notice our definition of formula in
section 2.4, also, for example, a Hilbert style
proofHilbert style systemHilbert style system is a
sequence of closed formulas
 such that Fi is an axiom or
follows by a rule of inference from Fj, Fk for j<i, k<i. A typical
inference rule is expressed in the form of hypotheses above a horizontal line
with the conclusion below as in modus poneusmodus ponens.
such that Fi is an axiom or
follows by a rule of inference from Fj, Fk for j<i, k<i. A typical
inference rule is expressed in the form of hypotheses above a horizontal line
with the conclusion below as in modus poneusmodus ponens.
This definition of a proof includes a specific presentation of
evidence that an element is in the class of all proofs.
The above form of a rule can be used to present any inductive definition. For
example, the natural numbers are often defined inductively by one rule with no
premise and another rule with one.
This definition of
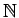 is one of the most basic inductive definitions.
It is a pattern for all others, and indeed, it is the clarity of this style of
definition that recommends it for foundational work.
is one of the most basic inductive definitions.
It is a pattern for all others, and indeed, it is the clarity of this style of
definition that recommends it for foundational work.



Next: Functions
Up: Introduction
Previous: Architecture of type theory
James Wallis
1999-09-17
