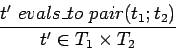Next: Inference mechanism
Up: Introduction
Previous: Level restrictions
What we have said so far lays out a basic structure for the theory. We start
with a class of terms. This is the linguistic material needed for
communication. We use variables and substitution of terms for variables to
express relations between terms. Let x, y, z be variables and s, t be
terms. We denote the substitutionsubstitution of term s for all
free occurrences of variable x in t by t[s/x]. The details of specifying
this mechanism vary from theory to theory. Our account is conventional and
general.
Substitution introduces a primitive linguistic relationship among terms
which is used to define certain basic computational equalities such as
![$ap(\lambda(x.b); a) = b[a/x]$](img528.gif) .
.
There are other relations expressed on terms which serve to define
computation. We write these as evaluation relations
definedness (
 )
)
Some terms denote types, e.g.
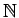 denotes the type of natural numbers.
There are type forming operations that build new types from others, e.g. the
Cartesian product
denotes the type of natural numbers.
There are type forming operations that build new types from others, e.g. the
Cartesian product
 of T1 and T2. Corresponding to a type
constructor like
of T1 and T2. Corresponding to a type
constructor like 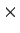 there is usually a constructor on elements, e.g. if
there is usually a constructor on elements, e.g. if
 then
then
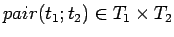 .
By the
Tait pre-evaluation condition above
.
By the
Tait pre-evaluation condition above
Part of defining a type is defining equality among its numbers. This is
written as s=t in T. The idea of defining an equality with a type produces
a concept like Bishop's sets (see [12,13]), that is
[12, p.63] said ``...a set is defined by describing what
must be done to construct an element of the set, and what must be done to show
that two elements are equal.''
The basic forms of judgmentjudgment in this type theory are
- t is a term
This is a simple context-free condition on strings of symbols that can be
checked by a parser. We stress this by calling these readable
expressions.
-
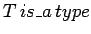
We also write 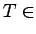 Type and prefer to write capital letters,
S,
T, A, B for types. This relationship is not decidable in general and cannot
be checked by a parser. There are rules for inferring typehood.
Type and prefer to write capital letters,
S,
T, A, B for types. This relationship is not decidable in general and cannot
be checked by a parser. There are rules for inferring typehood.
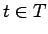 (type membership or elementhood)
(type membership or elementhood)
This judgement is undecidable in general.
- s=t in T (equality on T)
This judgement is also undecidable generally.



Next: Inference mechanism
Up: Introduction
Previous: Level restrictions
James Wallis
1999-09-17
![]() .
.
![]() )
)