T-Th 9:05
or
T-Th 11:15
in Olin 155

CS 1110: Introduction to Computing Using Python

Fall 2016

Assignment 2:
Call Frames

Due to CMS by Sunday, September 25th at 11:59 pm.

This is a simple written assignment where you are going to diagram a few call frames. This assignment should (hopefully) only take you two or three hours. So even if you are busy revising assignment 1, you should be able to do this assignment as well. With that said, keep track of the actual time that you spent on this assignment for the survey.

“Diagramming” is what we do in the lecture notes where we draw boxes to represent function calls and folders to represent the objects. These are a way of giving us a visual representation of what is going on in the computer when it runs Python. The purpose of this assignment is to solidify your understanding of how function calls work.

Learning Objectives

This assignment is design to help you understand the following concepts.

  • How to use call frames to model function execution.
  • The difference between a call frame and global space.
  • How folders represent Python's handling of objects.

Table of Contents

Authors: W. White, L. Lee, S. Marschner

Academic Integrity and Collaboration

Academic Integrity

This assignment is a slightly modified version of an assignment given in a previous semester. Please do this assignment without consulting (or seeking) previous solutions. Consulting any prior solution is a violation of CS1110's academic integrity policies.

Collaboration Policy

You may do this assignment with one other person. If you are going to work together, then form your group on CMS as soon as possible. This must be completed before you submit the assignment. Both people must do something to form the group. The first person proposes, and then the other accepts. You do not need to have the same partner as last time; you can change your partner with each assignment.

If you do this assignment with another person, you must work together. It is against the rules for one person to to fill out this assignment and just have the other person put their name at it. You should actively collaborate on this assignment. You may not collaborate with anyy other than your CMS partner.

Using the Python Tutor

We have demonstrated the Python Tutor several times in class. As you may realize, using the Tutor makes (parts of) this assignment really easy. We are perfectly okay with this. It is a good way to help you understand the formalism if you are particularly lost.

If you used the Python Tutor to help you with part of the problem, please cite this (for each part that you used it) in your submission. We will not take off any points if you use the Tutor and cite it. We only require a citation because it is part of our Academic Integrity Policy.

Getting Help

Even though this is just a written assignment, some of you may still have some difficulty with it. You might not completely understand how function calls work or the purpose of folders. If you are lost, please see someone in the course staff. This can be the course instructor, a TA, or a consultant. Furthermore, do not wait until the last minute, as the course staff is generally overwhelmed just before an assignment deadline.

Diagramming Conventions

Most of our diagramming conventions follow the lecture notes. However, just to be safe, we will make our conventions explicit here.

Diagramming Variables

A diagram for a variable should include the variable name and a box for the value. We we reassign a variable, old values are crossed out when they are replaced by new ones.

For example, here is a diagram for the variable b, currently holding the integer 2:

When writing the value, the only rule is to make sure it is unambiguous what the value is, and what type it is. Write floats with a decimal point or in scientific notation, strings with quotes around them, and so forth.

Diagramming Objects

All values in Python are objects, but we only bother to draw an object separately from variables referring to it if the object is mutable (e.g. the contents of the folder can be changed). All of the base types — int, float, bool, and str — are immutable. Therefore we draw all of these values inside the variable referring to them.

So far the only mutable objects we have seen are those with named attributes, like those of type Point3.

You will not be responsible for figuring out how to diagram an arbitrary object in this assignment. For any mutable object (which requires a folder), we will show you how to diagram the object. When you diagram an object you should obey the following conventions:

  • The folders identifier (ID, or true name) should be unique and go on the folder tab.
  • The type of the object should go at the top right of the folder.
  • The attributes should be listed inside the folder and diagrammed just like variables.

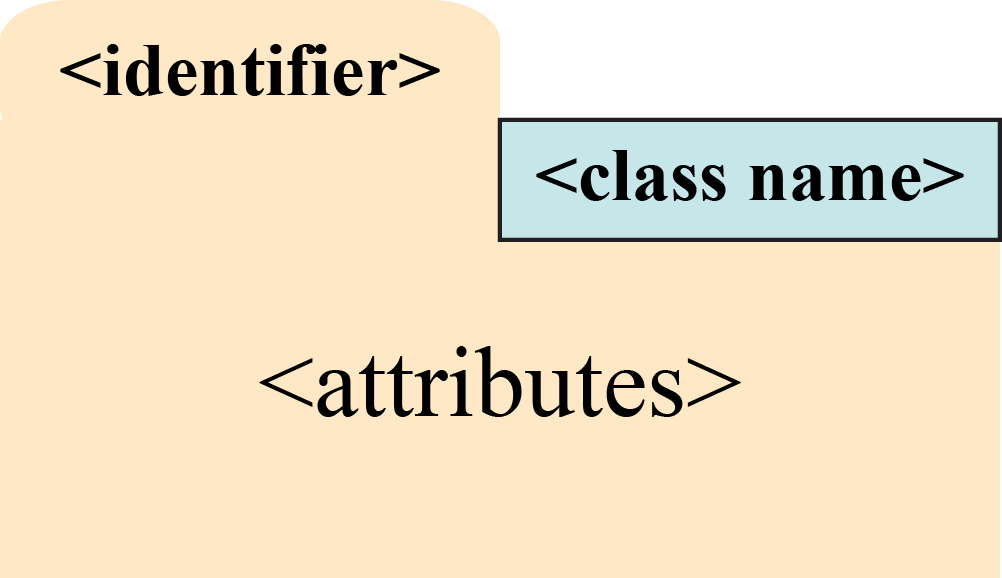
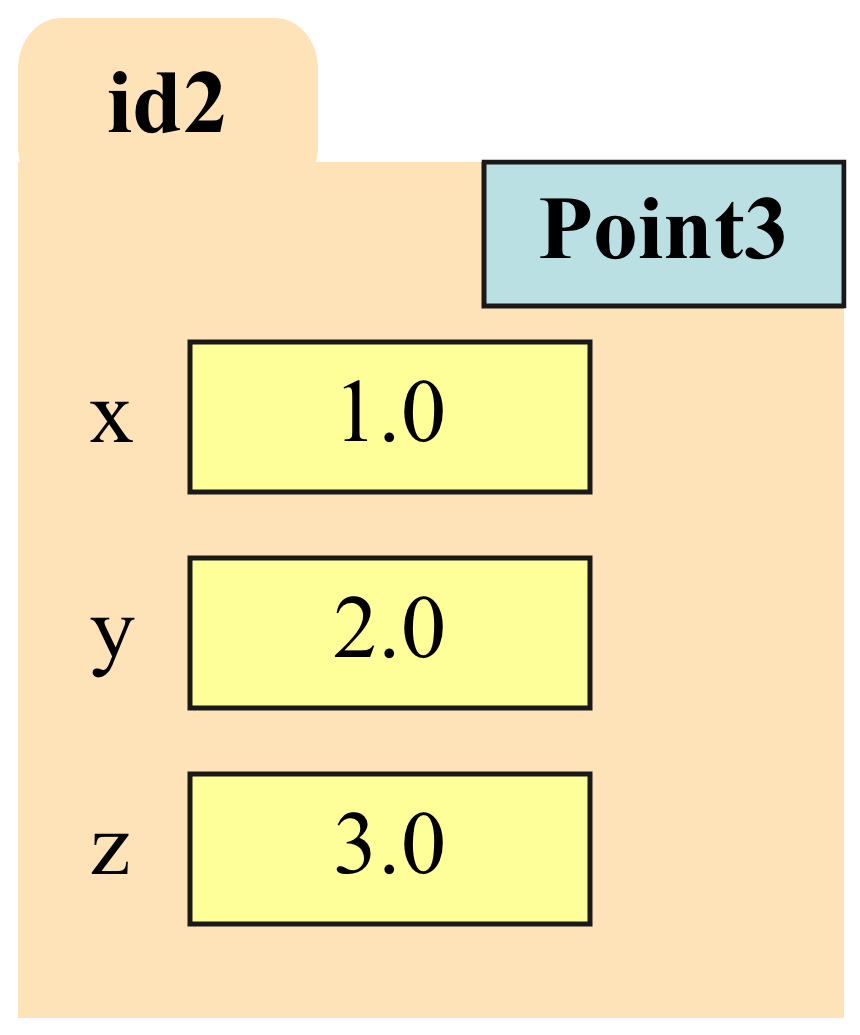
For example, a folder for an object of the type Point3 from class might look like this:

Diagramming Function Calls

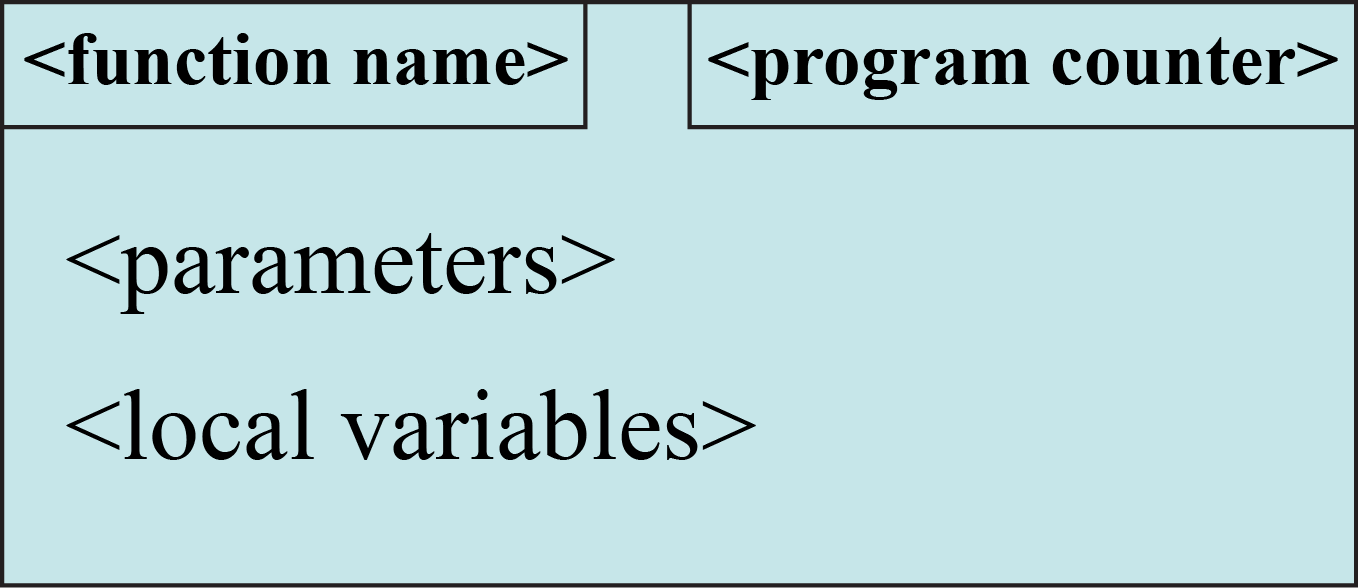
Call frames are the way we diagram the temporary workspace where the variables used during a call to a function are stored. Diagrams of frames should obey the following conventions:

  • The top left corner is a box with the function name.

  • The top right counter is the program counter. This is next line of code to execute in the function.

  • Unless otherwise stated, the first line of code after the function header corresponds to a counter value of 1.

  • Local variables and parameters are diagrammed in the frame body; we do not distinguish between them.

  • Local variables are not added until the instruction counter reaches the line where they are first defined.

See the lecture notes for more details on how to create a call frame. In order to help you with the instruction counter, we will always number the lines of code for you. For example, suppose we have the procedure 

  def print_name(last, first):
1      greet = 'Hello '+first+' '+last+'!'
2      print greet

If we execute the call print_name("White","Walker"), then the call frame starts out as follows:

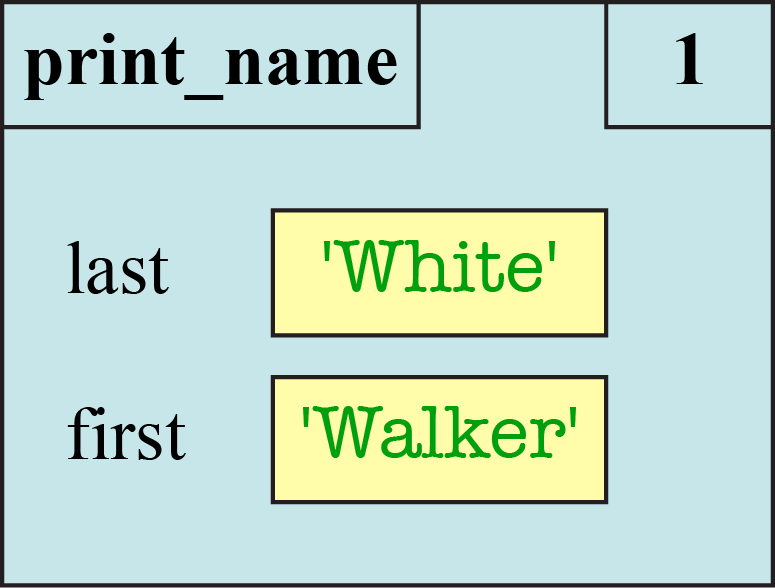
The Evolution of a Call Frame

A call frame is not static. As Python executes the body of the function, it alters the contents of the call frame. For example, after we have executed line 1, the call frame now looks as follows:

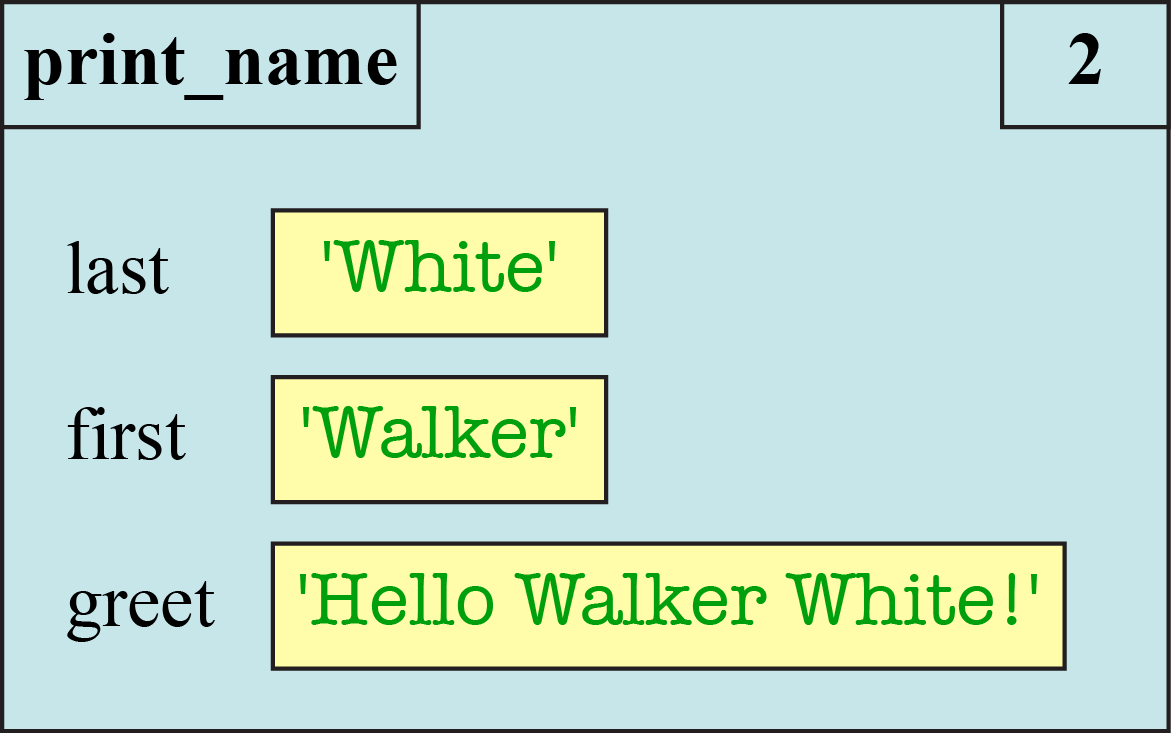
This is not a new call frame; this is the same call frame shown at a different point in time. The call frame does not go away until the function call is completed. When we diagram a call frame, we are actually diagramming a sequence of boxes to show how it changes over time.

As a general rule, we should draw a separate frame diagram for each value of the program counter, corresponding to a single line of Python code. The diagram above refers to the call frame after we finish line 1. Once we finish line 2, the diagram for the call frame is as shown below.

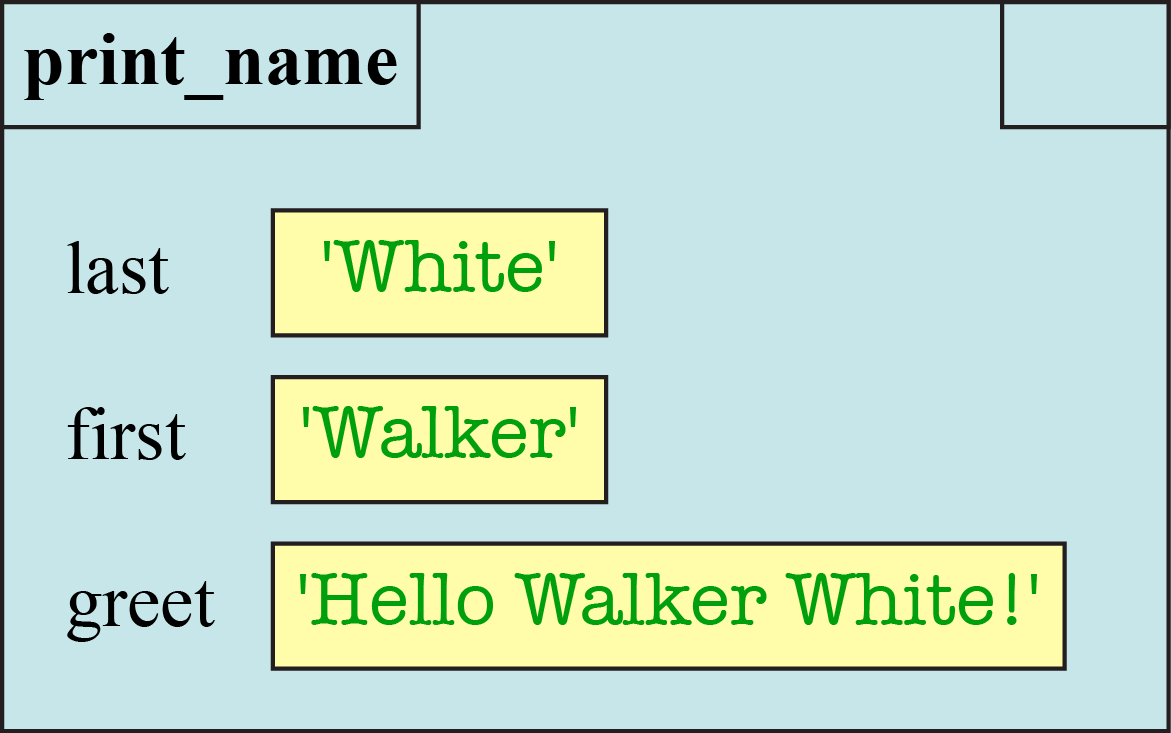
Note the instruction counter is blank. That is because there are no more instructions to execute. However, the call frame is not yet deleted. To represent the deletion of the call frame, we draw one more diagram, crossing out the frame.

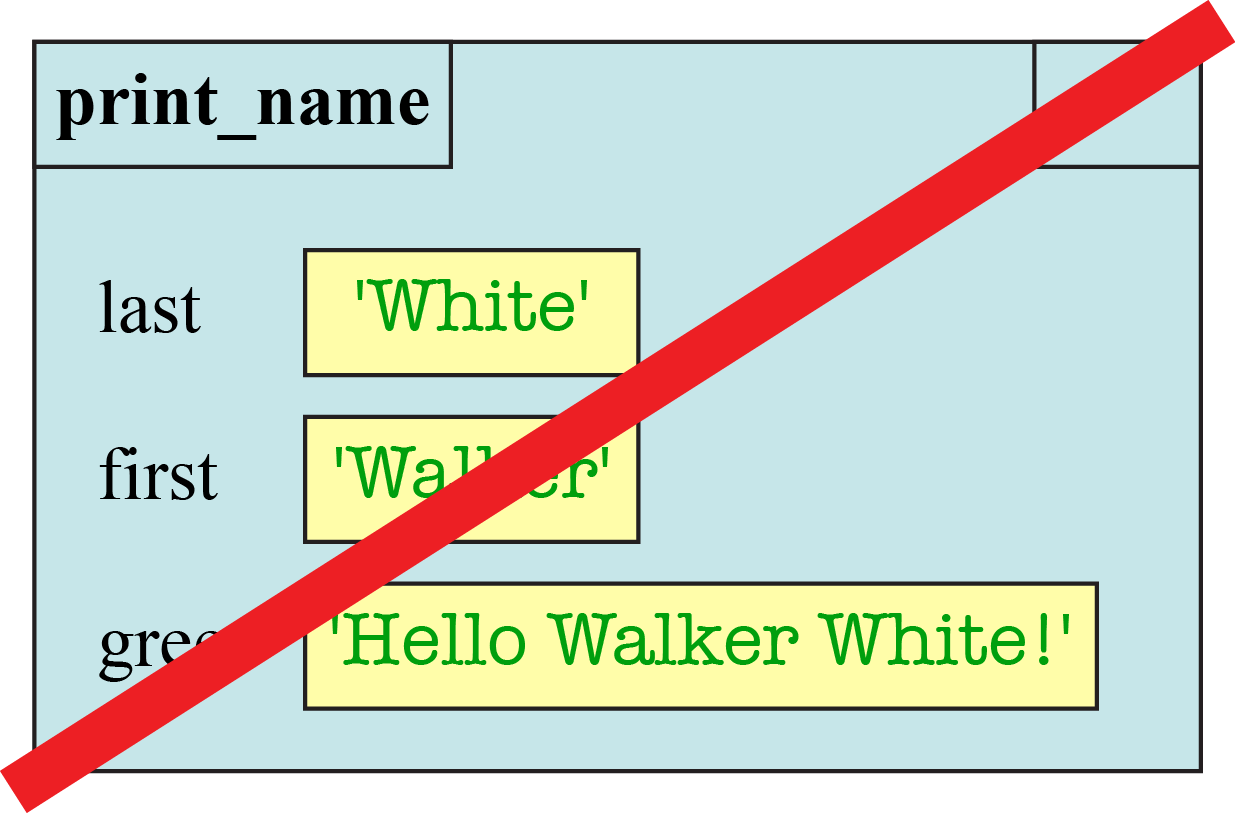
Frames and Return Values

Remember from class that fruitful functions have a return value. For example, consider the following variation on a function from class. 

  def to_centigrade(x):
1      tmp = 5*(x-32)
2      return tmp/9.0

When you execute a return statement, it makes a special variable called RETURN which stores the result of the expression. For example, suppose we have the function call to_centigrade(212). After executing line 1 of the code, above, the call frame is as follows:

return

When you execute the next line, the instruction counter becomes blank (because there is nowhere else to go), but you add the RETURN variable.

return-2

If you play with the Python Tutor, you will note that it always adds a RETURN variable, even for procedures (i.e. functions with no return statement). In that case it stores the value None into the RETURN variable. For example, when processing the call print_name("White","Walker"), this is what the Python Tutor says that the frame looks like just before it is erased.

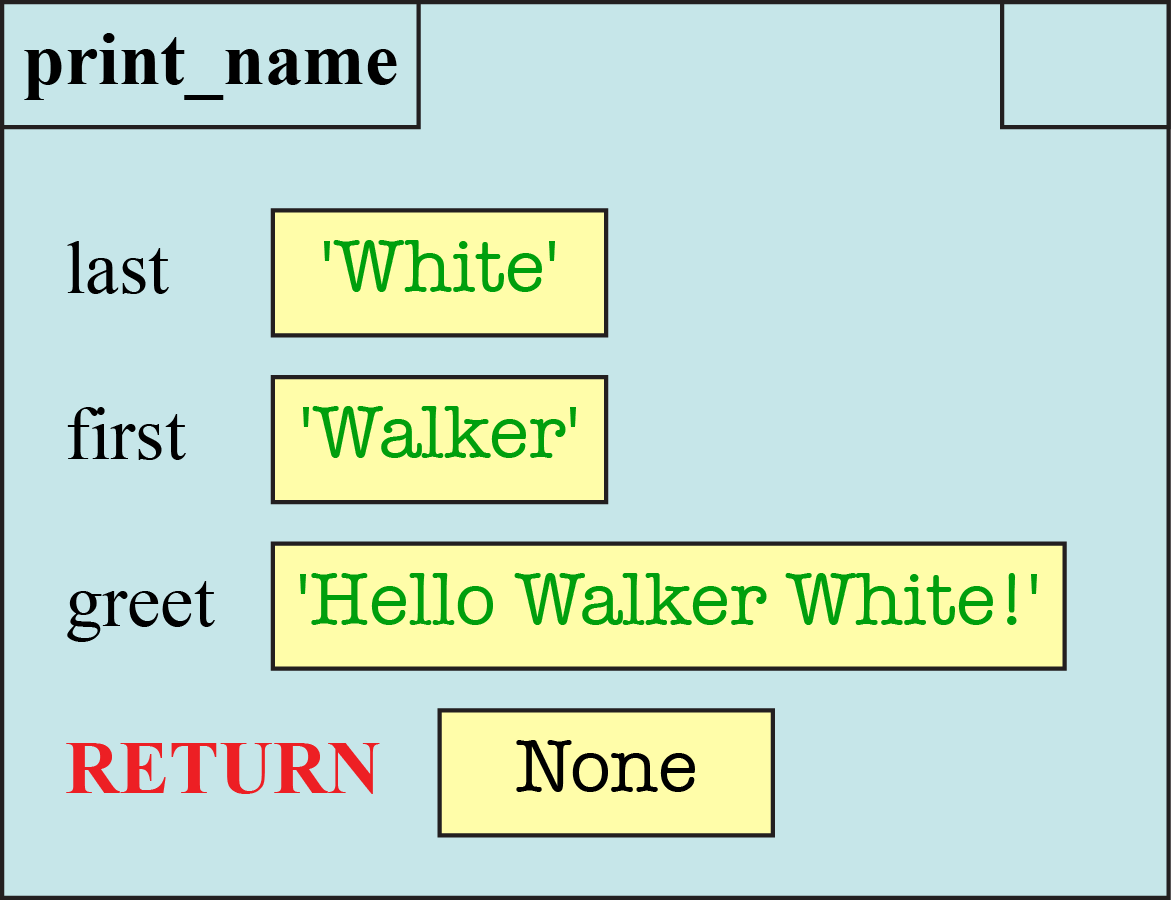
We are not following this convention, and you are not expected to do this. You should only add a RETURN variable for fruitful functions.

Frames and Global Space

Remember that you can use a function call as an expression. The call evaluates to the result of the return statement. If this call is used in an assignment statement, the is a way to copy from the RETURN variable to another place in memory, such as global space. For example, the call 

  y = to_centigrade(212.0)

will copy the final result (100.0) into the global variable y.

If function call is used in an assignment statement, then the value in the box is not changed until the step where you erase frame. In fact, if this is the first time that you are assigning the variable, you do not even create the box for the variable until the frame is erased.

You should denote changes to global space right next to the diagram for the frame. In our example above, that your diagram before erasing the frame is as follows:

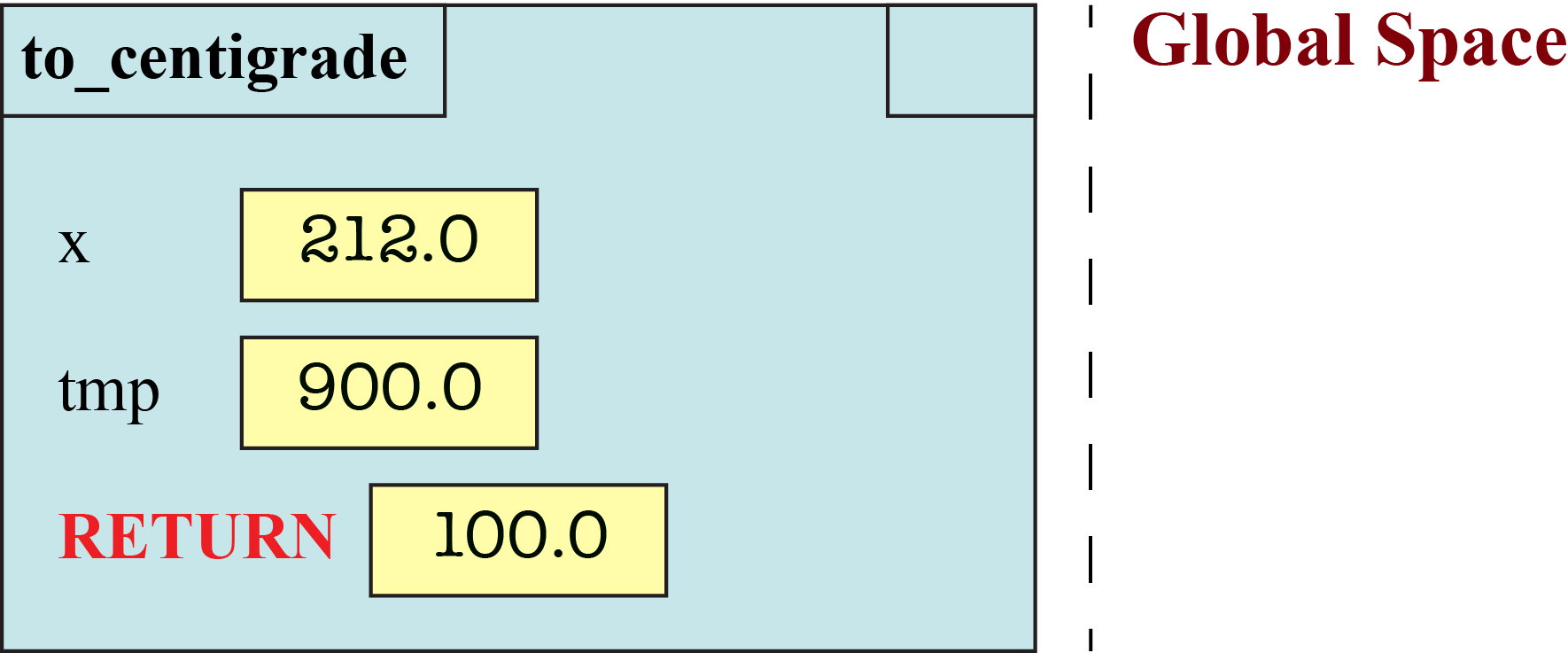
return-3

When you do erase the frame, the global space has changed to

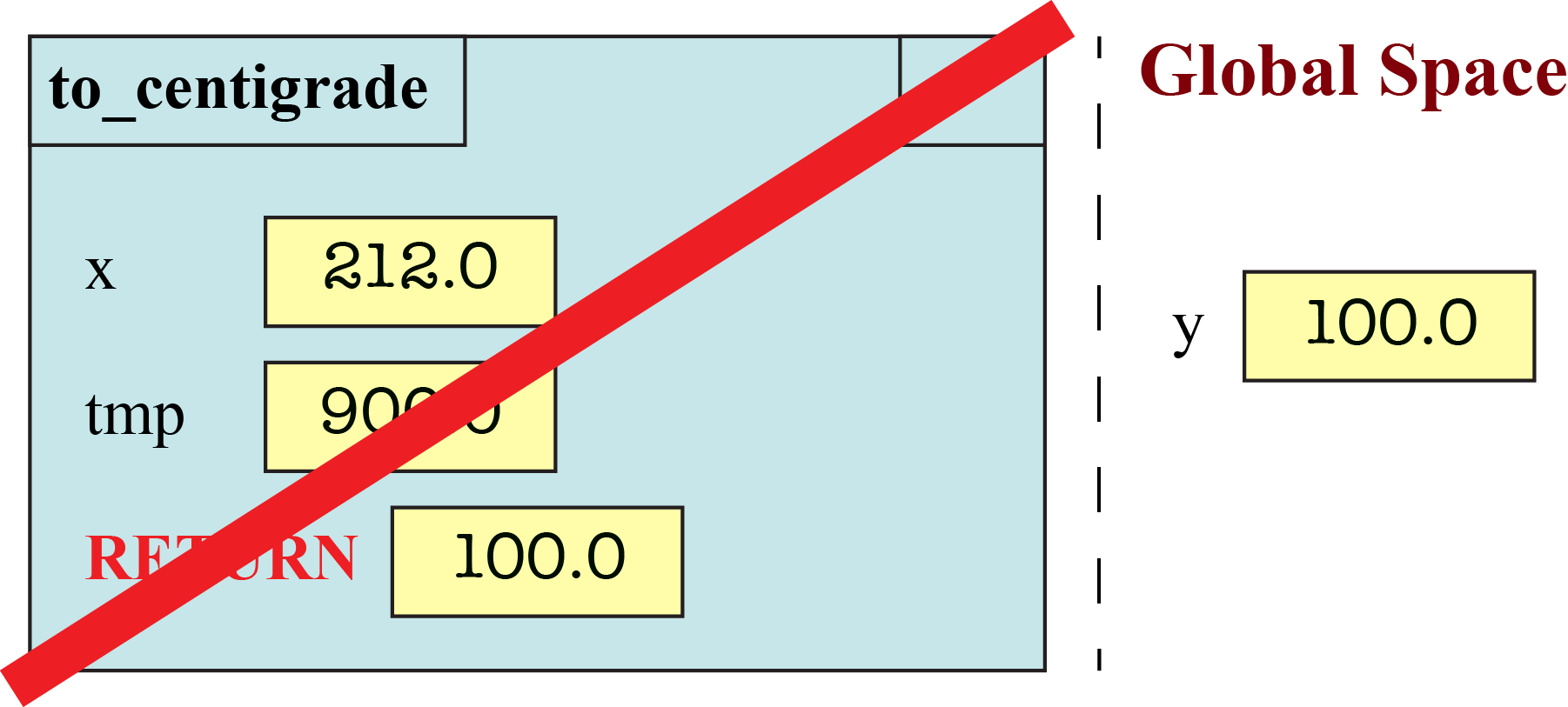
return-3

Modules and Functions in Global Space

As we saw in class, global space also has variables for the function and module names. For example, when you define a function, it creates a folder for the function body and stores the name of that folder in a variable with the same name of the function.

We do not want you to draw these variables in global space. You can ignore what happens to function definitions (and module importing) for now.

Assignment Instructions

Remember that there are three memory locations that we talked about in class: global space, call frames, and heap space. Every time that you execute a line of code, these can all change. We want you to draw pictures to show how they change over time.

For each problem, you will be given a function call. We want you to diagram the execution of four different function calls (one each in Part A, C, B, and D). You will draw a separate diagram for each line of Python that is executed (and only those lines that are executed). We also want you to draw one last diagram crossing the frame off at the end.

Some of the problems below will have associated values in both global space and heap space. For those problems, you should also diagram the evolution of both global space and heap space. For each line of code, next to the diagram for the call frame, you should redraw both global space and heap space.

Important: You must pay close attention to types in this assignment. The value 3 is an integer while the value 3.0 is a float. Hence they are different values. If you answer with an integer like 3 when the correct answer is a float like 3.0, we will deduct points.

Function max

The function max is built into Python. However, if we were to design it ourselves, it might look like this: 

   def max(a,b):
       """Returns: max of a and b
       
       Precondition: a and b are numbers"""
1      maximum = a
2      if (a < b):
3          maximum = b
4      return maximum

Part A: Diagram the Execution of c = max(1,2)

Draw the execution of the statement c = max(1,2). You will need to draw the evolution of the call frame over time. This will require several diagrams. You will need a diagram when the frame is created, and another when it is erased. In between, you will need a diagram for each line of code that is executed (and only the lines which are executed). Remember, this is one call frame, but several diagrams showing how the call frame changes over time.

When an assignment changes the value of an existing variable in the frame, we would like you write the old value in the box, cross it out, and write the new value in the box.

In addition to the diagrams for the (evolution of the) call frame, you also need to diagram the evolution of the global variable c. In particular, global space starts out empty (we are ignoring the variable for the function max); we want to know when the variable c appears in global space. You do not need to draw the evolution of heap space, as there is nothing interesting in heap space for this problem.

Part B: Diagram the Execution of d = max(b,a)

For this next part, suppose that you have the following (global) variables:

As we said in class, these variables are global variables and are not the same as the parameters of max, which are local to that function.

Repeat the previous exercise for the statement d = max(b,a). Once again, you need to draw the evolution of global space right next to each individual frame diagram. The difference is that this time global space does not start out empty. In addition, the new global variable is now named d.

Functions on Point3 Objects

The next two problems have to do with the Point3 class introduced in lecture. Objects of the Point3 class have three attributes: x, y, and z. These objects are created by the constructor call Point3(x,y,z).

When dealing with objects, you should remember that a variable does not contain an object; it can only hold the identifier of the object. Therefore, the assignments 

  p = Point3(1,2,3)
  q = Point3(4,5,6)
would produce the following contents in both global and heap space

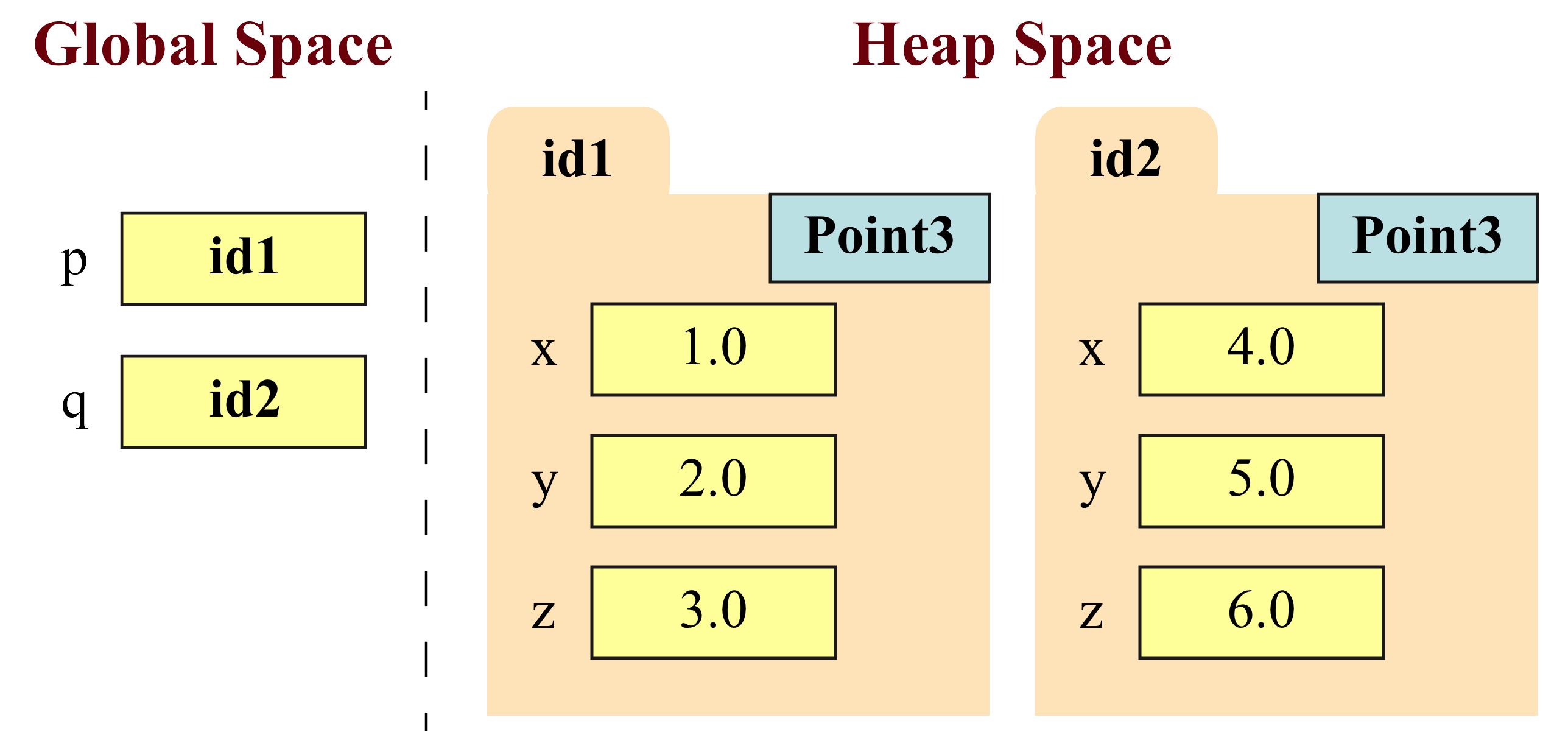
folder-variables

In this case we have folders representing two Point3 objects, and two global variables storing these object identifiers. We made up the folder identifier numbers, as their value does not matter. If we ask you to make a Point3 object, you should feel free to make up the identifier number, but make sure it is different from the ones currently in p and q.

Part C: Diagram the Execution of rot_y(p)

The function rot_y(q) function is a variation of the cycle_left(q) function demonstrated in class. It takes a point as input and swaps the x and z attributes; the y attribute is left unaltered. This is a rotation around the y axis. We define this function as follows: <

   def rot_y(q):
       """Swap the x and z attributes of q

       Example: The point (1,2,3) becomes (3,2,1)

       Parameter q: the point to rotate
       Precondition: q is (refers to, contains the ID of) a point object"""
1      tmp = q.x
2      q.x = q.z
3      q.z = tmp

The function rot_y is a procedure (it has no return statement) and so it does not need to be used in an assignment statement. Hence the call rot_y(p) is a statement by itself.

Diagram the call rot_y(p) given the global variables and heap space shown above. Your answer will in include a sequence of diagrams for the call frame for rot_y(p). Again, you should have a diagram when the frame is created, a diagram for each line executed, and a diagram for deleting the frame.

Your diagrams should also include the evolution of the global variables p and q, and the corresponding objects in heap space. You should draw the global space and heap space next to every single diagram in your evolution of the frame. If the contents of any global variable change, or the contents of the object folders are altered, you should cross out the old value and write in the new value.

Part D: Diagram the Execution of p = rot2_y(q)

The function rot2_y(q) is similar to rot_y(q), except that it is a fruitful function instead of a procedure. We define the function as follows: 

   def rot2_y(q):
       """Returns: A copy of q with the x and z attributes swapped

       Example: rot2_y with argument (1,2,3) creates the point (3,2,1)

       Parameter q: the point to rotate
       Precondition: q is (refers to, contains the ID of) a point object"""
1      r = Point3(0.0,0.0,0.0)
2      r.x = q.z
3      r.y = q.y
4      r.z = q.x
5      return r

Diagram the execution of the statement p = rot2_y(q) given the global variables and heap space shown above. Assume that you are starting over with p and q; do not include any changes from Part C.

As always, you should have a diagram when the frame is created, a diagram for each line executed, and a diagram for deleting the frame. You should draw the global space and heap space next to every single diagram in your evolution of the frame. If the contents of any global variable change, or the contents of the object folders are altered, you should cross out the old value and write in the new value.

Working in Reverse

So far in this assignment, we have given you a function definition and asked you to draw the diagram for a function call. Now we want you to do the reverse. We give you the diagrams for several function calls and ask you to write the corresponding definition. All you have to do is show the Python code. Any function definition is correct so long as it produces the frame shown for each call.

Part E: Define the function dist(x,y)

The function dist has the following specification: 

   def dist(x,y):
       """Returns: The number line distance between x and y

       Example: dist(2,5) returns 3
       Example: dist(5,2) returns 3

       Parameter x: the starting point
       Precondition: x is a number
       
       Parameter y: the ending point
       Precondition: y is a number"""

The following diagrams illustrate the function calls dist(5,3) and dist(2,7), respectfully.

dist

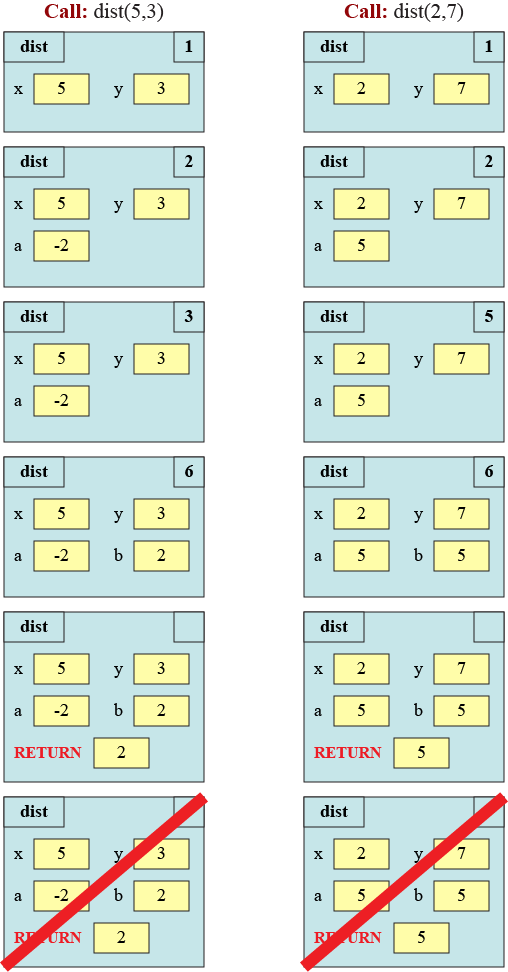
Complete the function definition.

Hint: Your solution cannot use the built-in function abs, as that would technically create a call frame for that function as well.

Finishing the Assignment

When you finish the assignment, put your name and netid at the top of the page. Otherwise, we will not know that the assignment is yours, and we cannot give you credit for your work. If you are working with a partner, then the partner's name must be on the assignment as well. In addition, to help us out with organization, please underline your last name(s).

Creating a PDF for Submission

Because of the size of this class, we want you to submit this assignment online through CMS. To do this, you must submit your file as a PDF. If you created your assignment on a computer, this should be relatively easy. Otherwise, you will need to scan your paper as a PDF. There are scanners in Olin and Uris Library to help you with this.

Your solution must be a single PDF file. You cannot submit multiple PDF files. If your scanner makes more than one file, you must combine them together. On Windows, the program PDFtk can merge multiple PDF files into one file. In OS X, the built-in application Preview can be used to merge PDF files.

Your final file must be less than 100MB in size; ideally it should be less than 10MB. This should not be a problem as long as the resolution is reasonable. Do not scan at a higher resolution than 300 dpi. This is not an art class; we do not need that level of detail. If your file is too large, use the web page SmallPDF to reduce your file size.

Your submission must be uploaded to CMS by Sunday, September 25th at 11:59 pm. If you are planning to scan your submission, we recommend that you finish long enough ahead of time to give you time to scan.

Survey

Once again, this assignment comes with a survey on CMS. This survey asks how long you spent on the assignment, your impression of the difficulty, and what could be done to improve it.

Please try to complete the survey within a day of turning in this assignment. Remember that participation in surveys compromise 1% of your final grade. We also ask that you be honest in your answers.


Course Material Authors: D. Gries, L. Lee, S. Marschner, & W. White (over the years)