Chapter 5 Contagion in Social Networks

Let us now return to the question of how the adoption of a product spreads through the network. In particular, we are interested in studying when a product spreads to the whole network. We start by analyzing this problem in the simpler model of plain networked coordination games (without intrinsic values and without weighted edges), but then remark how the analysis extends also to the more complex models.

5.1 Cascades

Recall that in the plain model, a node decides to choose $X$ if the fraction of its neighbors choosing $X$ exceeds some global adoption threshold $t = \frac{y}{x + y}$ (recall that $x$ is the utility of coordinating on $X$ and $y$ is the utility of coordinating on $Y$ ). We are interested in determining when $X$ will spread to the entire network; as we observed in Figure 4.1, there exist networks with equilibria where both $X$ and $Y$ are played (and thus, even if players best respond, $X$ will never take over the whole network).

The contagion question If we “infect” an initial set of nodes—think of these as “early adopters” of the product—with a choice of $X$ so that they will choose $X$ no matter what, will $X$ spread to the entire network if players follow best-response dynamics? (For instance, what if we decide to promote our Android phone by giving a small number of “influential” people one for free?) We refer to such a spread as a cascade; let us formalize this notion.

Definition 5.1. Given a plain networked coordination game $𝒢$ induced by a graph $G = (V, E)$ and coordination utility $Q$ , we say that a set $S \subseteq V$ is cascading with respect to $𝒢$ if the following process always ends with all nodes in $V$ choosing $X$ :

Start off with a strategy profile $\vec{a} = (X_{S}, Y_{- S})$ , where every node in $S$ chooses $X$ , and all other nodes choose $Y$ .
Run BRD from $\vec{a}$ but where the process is restricted to only nodes in $V ∖ S$ best responding (i.e., nodes in $S$ never change from $X$ , but the others may change strategies by best responding).

Note that since BRD always converges in $𝒢$ , it must also converge if we restrict the dynamics to only allowing a subset of the players to best respond—every best-response sequence with respect to the restricted set of players is clearly also one with respect to the full set of players (so if there exists some “loop” with respect to the restricted set, such a loop also exists with respect to the full set). Thus, the above contagion process (where the BRD is restricted to only the players in $V ∖ S$ ) will always terminate. (Note, however, that the final strategy profile may not necessarily be a PNE: The “early-adopters” in $S$ may have a profitable deviation; the final strategy, however, is a PNE if we assume that the nodes in $S$ do not have the option of switching. Later on, in Section 5.3, we shall consider a model where also the nodes in $S$ can switch strategies.)

5.2 Characterizing Cascades

We now present a simple condition that exactly characterizes when a set $S$ is cascading. To do this, we will define a notion of the density of a set of nodes.

Definition 5.2. Given an undirected graph $G = (V, E)$ and a set of nodes $S \subseteq V$ , we say that $S$ has density $t$ if for every node $v \in S$ , the fraction of $v$ ’s neighbors that are inside $S$ is at least $t$ ; that is, for all $v \in S$ ,

\frac{| N (v) \cap S |}{| N (v) |} \geq t .

Theorem 5.1. Given a plain networked coordination game $𝒢$ induced by $G = (V, E), Q$ with adoption threshold $t$ , a set $S$ is cascading with respect to $𝒢$ if and only if there does not exist a set of nodes $T \subseteq V ∖ S$ having density $1 - t$ (with respect to $G$ ).

Proof. We prove each direction separately.

The “only-if” direction: Assume for contradiction that $S$ is cascading yet the network contains a set $T \subseteq V ∖ S$ of density $1 - t$ . Consider the first round in the BRD process when some node $v \in T$ becomes “infected” (i.e., switching to $X$ ). At this point, all other nodes in $T$ play $Y$ (since $T$ does not have any intersection with $S$ ); thus, by the density requirement of $T$ , the fraction of $v$ ’s neighbors that are playing $Y$ is at least $1 - t$ . Consequently, at most a $t$ fraction of $v$ ’s neighbors play $X$ , which contradicts that $v$ would switch.

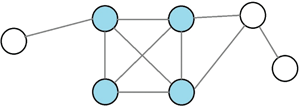
**Figure 5.1:** The blue nodes form a $\frac{3}{4}$ -dense set: every node in this set has at least $\frac{3}{4}$ of its neighbors in the set.

The “if” direction: Consider some set $S$ that is not cascading. We show that the network must contain a set $T \subseteq V ∖ S$ of density $1 - t$ . As noted above, the cascade process (i.e., BRD restricted to players in $V ∖ S$ ) always converges in the game. Consider some final outcome of the process where not everyone switched to $X$ (such an outcome must exist since $S$ is not cascading) and let $T$ be the set of nodes playing $Y$ in this outcome. Since nodes in $S$ never switch actions (and always play $X$ ), $T \subseteq V ∖ S$ . Let us now argue that $T$ must have density $1 - t$ . In fact, if it did not, some node $v \in T$ has a greater than $t$ fraction of its neighbors outside of $T$ and would thus want to switch (since by construction all nodes outside $T$ play $X$ ), so the outcome could not be final.

■

An interesting consequence of the above theorem is that the order of the players in the cascade process (i.e., the restricted BRD process) is irrelevant in determining whether or not a set $S$ cascades!

The computational complexity of finding the small cascading sets Ideally, we would like to have a computationally efficient way of finding a small cascading set. It turns out that this problem is computationally intractable (technically, NP-hard), as shown by [KKT03]. However, in practice, the “greedy” strategy of sequentially infecting players that increase the cascade as much as possible appears to work well (although it may fail miserably on worst-case instances).

5.3 Strong Cascades

The notion of a cascading set assumes that the original set $S$ of “early adopters” never changes actions—that is, they do not participate in the BRD. We can consider an even stronger notion of cascading where the early adopters only need to start off playing $X$ , but then may themselves participate in BRD (including potentially switching to the choice $Y$ if many of their neighbors are playing it).

Definition 5.3. Given a plain networked coordination game $𝒢$ induced by a graph $G = (V, E)$ and coordination utility $Q$ , we say that a set $S \subseteq V$ is strongly cascading with respect to $𝒢$ if BRD from the outcome $(X_{S}, Y_{- S})$ always ends with all nodes in $V$ choosing $X$ .

The following theorem provides a sufficient condition for a set of nodes to be strongly cascading.

Theorem 5.2. Given a plain networked coordination game $𝒢$ induced by $G = (V, E), Q$ with adoption threshold $t$ , a set $S$ is strongly cascading with respect to $𝒢$ if

$S$ has density t (with respect to $G$ ); and,
there does not exists a set of nodes $T \subseteq V ∖ S$ having density $1 - t$ (with respect to $G$ ).

Proof. Consider some set $S$ of density $t$ . By the same argument as in the proof of Theorem 5.1, nodes in $S$ will never change from playing $X$ (as at least a fraction $t$ of their neighbors are in $S$ and hence playing $X$ at all times). Hence, running BRD from $(X_{S}, Y_{- S})$ is equivalent to running BRD from $(X_{S}, Y_{- S})$ but restricting the best-responding players to $V ∖ S$ , and so in this particular case $S$ is strongly cascading if and only if it is cascading, which by Theorem 5.1 concludes the proof.

■

An important interpretation of this theorem is that if you want to introduce a new product to a market where it is easy for people to switch products, carefully pick the initial set of nodes $S$ to which to promote the product so that (a) $S$ forms a sufficiently dense cluster (or else, they may decide to switch back to the old product) and (b) there is no sufficiently dense cluster of users outside of $S$ .

5.4 Dealing with Subjective Thresholds

So far we have only considered plain networked coordination games. Let us turn to analyzing also more general ones. Recall that for the case of plain networked coordination games, each player decides to switch to $X$ if the fraction of their neighbors choosing $X$ exceeds some global adoption threshold $t$ . As mentioned, for more general networked coordination games, this no longer holds; rather, each player $v$ has their own subjective adoption threshold $t (v)$ . The results for cascading and strongly cascading sets are easily extended to this setting by considering a more general notion of density, where a set $S$ is said to have density $t (\cdot)$ if, for each node $v \in S$ ,

\frac{N (v) \cap S}{N (v)} \geq t (v) .

In fact, we may further generalize this notion to also deal with networked coordination games with weighted edges by considering a notion of weighted density: a set $S$ is said to have weighted density $t (\cdot)$ if, for each node $v \in S$ ,

\frac{\sum_{j \in N (i) \cap S} w (i, j)}{\sum_{j \in N (i)} w (i, j)} \geq t (v) .

All the results on contagion still apply to networked coordination games with weighted edges, if we replace density with weighted density in the theorem statements.

Notes

Contagion in social networks was first studied by Morris [Mor00]; Theorem 5.1 is a slight variant of a theorem from [Mor00]. The treatment of strong cascades is new.