where
Hi is an assertion or a type and
xi is either a label or a variable
respectively. The
xi are all distinct.
G is always an unlabeled formula.
We can also refer to the hypothesis by number,
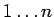
,
and we refer to
G as the 0-th component of the sequent. We abbreviate a sequent by
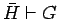
for
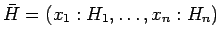
;
sometimes
we write
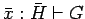
.
James Wallis
1999-09-17