


Next: Formal proofs
Up: Formulas
Previous: Typing judgments
Here are examples, for
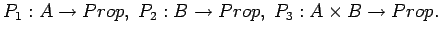
is a
closed formula.
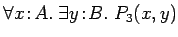 is an
immediate subformula which is also closed, but
is an
immediate subformula which is also closed, but
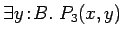 is not closed since it has the free variable
is not closed since it has the free variable 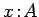 ;
this latter formula is well-formed in the context
;
this latter formula is well-formed in the context 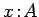 .
.
The atomic subformulas are
P1(x), P2(y), and
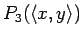 which are formulas in the context
which are formulas in the context
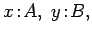 and the typing judgment
and the typing judgment
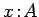 ,
,
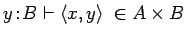 is used to
understand the formation of P3(x, y) (which is an abbreviation of
is used to
understand the formation of P3(x, y) (which is an abbreviation of
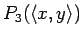 ).
).
James Wallis
1999-09-17
![]() which are formulas in the context
which are formulas in the context
![]() and the typing judgment
and the typing judgment
![]() ,
,
![]() is used to
understand the formation of P3(x, y) (which is an abbreviation of
is used to
understand the formation of P3(x, y) (which is an abbreviation of
![]() ).
).