CS 6115 Schedule Project Blog Guidelines Resources

CS 6115 - Course Blog

Table of Contents

  1. Anna Mazhar — Formalizing AVL Trees in Coq
  2. Aaron Yagnik — Formalizing and Verifying Red-Black Trees in Coq
  3. Emmanuel J. Suárez Acevedo and Max Fan — Outcome Logic in Coq
  4. Ernest Ng and Laura Zielinski — Verifying Brzozowski and Antimirov Derivatives
  5. Gerardo Garcia Teruel Noriega — Verifying Distributed Consensus Algorithms
  6. Goktug Saatcioglu — Secure Declassification
  7. Kabir Samsi — Formally Verifying Operational Semantics In Packet Scheduling
  8. Mark Barbone — Concurrent KAT: decidable program properties for shared-memory concurrency
  9. Yulun Yao — Proving compiler correctness for a sequential hardware description language that describes parallel behaviors

Formalizing AVL Trees in Coq

Anna Mazhar

Introduction

Balancing binary search trees is essential for optimizing data structure performance, especially when maintaining ordered data efficiently. This work focuses on formalizing AVL Trees, a type of self-balancing binary search tree, using Coq. Here, I explore defining AVL properties and implementing core operations like insertion and deletion, ensuring correctness through Coq's rigorous proof system.

AVL trees guarantee that the height difference (balance factor) between subtrees is at most 1, maintaining logarithmic height. This balance ensures efficient lookups, insertions, and deletions, all operating in O(logn) time.

AVL Trees

Quick primer on AVL Trees

  1. Binary Search Tree (BST) Property:

    • Each node has at most two children.
    • Values in the left subtree are smaller, and values in the right subtree are larger than the current node.

  2. Balance Factor:

    • For every node, the balance factor is calculated as: $$ Balance Factor = Height of Left Subtree - Height of Right Subtree $$
    • An AVL tree ensures the balance factor of every node is in the range [-1,1].

  3. Height Maintenance:

    • When the balance factor goes outside the range [-1,1], the tree is rebalanced through rotations.

Rotations in AVL Trees

Rotations restore balance by reorganizing nodes:

AVL Tree Example
  1. Single Rotation:
    • Left Rotation: Applied when a right-heavy subtree causes imbalance.
    • Right Rotation: Applied when a left-heavy subtree causes imbalance.
  2. Double Rotation:
    • Left-Right Rotation: A left rotation followed by a right rotation.
    • Right-Left Rotation: A right rotation followed by a left rotation.

AVL in Coq

The AVL tree is defined as an inductive type. Each node stores:

An AVL tree is inductively defined as:

Inductive AVLTree : Type :=
  | Empty : AVLTree
  | Node : AVLTree -> nat -> AVLTree -> nat -> AVLTree.

Focusing on Properties

The approach prioritizes the formalization of key properties:

  1. Binary Search Tree (BST) Property: Every node's value is greater than all values in its left subtree and smaller than all values in its right subtree.
  2. Balance Invariant: The difference in height between the left and right subtrees of any node is at most 1.
  3. Height Validity: Heights of nodes must align with the recursive structure of the tree since heights stored at each node are crucial for computing the balance factor.

These properties are not only fundamental to AVL trees but also ensure correctness and efficiency for operations performed on them.

AVL Operations

The following are the operations for which we must ensure adherence to the above the properties:

Key Properties Definitions

Order Invariant

The ForallT predicate is used in the definition of isBST to enforce the binary search tree property by constraining the values in the left and right subtrees of each node. Specifically, ForallT (fun x => x < v) l ensures all values in the left subtree are strictly less than the current node's value, while ForallT (fun x => x > v) r ensures all values in the right subtree are strictly greater. This structure is critical for formally verifying that the BST property is maintained across recursive operations, such as insertion.

Fixpoint ForallT (P: nat -> Prop) (t: AVLTree) : Prop :=
  match t with
  | Empty => True
  | Node l v r _ => P v /\ ForallT P l /\ ForallT P r
  end.

Inductive isBST : AVLTree -> Prop :=
| isBST_Empty : isBST Empty
| isBST_Node : forall l v r h,
    ForallT (fun x => x < v) l ->
    ForallT (fun x => x > v) r ->
    isBST l ->
    isBST r ->
    isBST (Node l v r h).

The rebalance operation restores the AVL balance property if it is violated. This checks for the balance factor and accordingly performs left or right or a combination of both rotations. The rebalance operation performed after every insert and delete operation.

Definition rebalance (t : AVLTree) : AVLTree :=
  match balance_factor t with
  | bf =>
      if Z.ltb 1 bf then
        (* bf > 1 case *)
        if Z.geb (balance_factor (match t with | Node l _ _ _ => l | _ => Empty end)) 0 then
          rotate_right t
        else
          match t with
          | Node l v r h =>
              rotate_right (mkNode (rotate_left l) v r)
          | _ => t
          end
      else if Z.ltb bf (-1) then
        (* bf < -1 case *)
        if Z.leb (balance_factor (match t with | Node _ _ r _ => r | _ => Empty end)) 0 then
          rotate_left t
        else
          match t with
          | Node l v r h =>
              rotate_left (mkNode l v (rotate_right r))
          | _ => t
          end
      else
        (* bf within [-1, 1] *)
        t
  end.

To prove the preservation of the order invariant in the rebalance operation, we prove the following theorem:

Lemma rebalance_preserves_isBST : forall t,
  isBST t -> isBST (rebalance t).

To prove order invariant in insert operation, helper lemmas like ForallT_insert and rebalance_preserves_isBST are used to manage the structural changes during insertion. ForallT_insert establishes that the predicate P continues to hold for all elements in the updated tree after inserting a new element k. This is essential for propagating the ForallT constraints across recursive calls. Meanwhile, rebalance_preserves_isBST ensures that balancing operations required to maintain AVL tree height properties do not violate the BST ordering constraints. These lemmas modularize the proof, allowing a clean separation of concerns between structural changes due to insertion and the rebalancing operations, ultimately proving that isBST holds for the resulting tree. The skeleton code is outlined below:

Lemma ForallT_insert : forall (P : nat -> Prop) (t : AVLTree),
    ForallT P t -> forall (k : nat),
      P k -> ForallT P (insert k t).

Lemma insert_bst : forall (x : nat) (t : AVLTree),
  isBST t -> 
  isBST (insert x t).

Similar efforts are required for delete operation proof simplication, however, it turned out to be more complex and completing it remains our future work. The source code includes the progress made so far. The following are key lemmas needed to prove.

Lemma ForallT_delete : forall (P : nat -> Prop) (t : AVLTree),
    ForallT P t -> forall (k : nat),
      P k -> ForallT P (delete k t).

Lemma insert_bst : forall (x : nat) (t : AVLTree),
  isBST t -> 
  isBST (delete x t).

Balance Invariant

For any balanced AVL tree, the balance factor at every node is within the range [-1, 1]. We prove it with the following lemma:

Lemma balance_factor_bounded : forall t,
  isBalanced t -> Z.abs_nat (balance_factor t) <= 1.

We could not make a significant progress here, however, we defined all the definitions of theorems in the code. Some are outlined below:

The rebalance operation performed after every insert and delete operation hence we should verify its balance property.

Lemma rebalance_preserves_balance : forall t,
  isBalanced t -> isBalanced (rebalance t).

The insert operation should maintain the AVL balance invariant

Theorem balanced_insert : forall t x,
  isBalanced t -> isBalanced (insert x t).

The delete operation should maintain the AVL balance invariant

Theorem balanced_delete : forall t x,
  isBalanced t -> isBalanced (delete x t).

Future Work

We managed to verify the order invariant of rebalance and insertion, however, we underestimated the complexity of delete operations. Though we made significant progress on its proof, completing it remains our future work. Same goes for its balance invariant proofs. Another interesting work to look at would be the formal verification of other balanced binary search trees, such as Red-Black trees or Weight-Balanced trees. This work features simple operations however future work can also cover bulk operations of AVL like merging, splitting, or batch insertions and deletions. Once complete specifications are defined, the correctness of other AVL trees can also be verified.

Formalizing and Verifying Red-Black Trees in Coq

Aaron Yagnik

Project Overview

I am building an implementation of the Red-Black Tree data structure in the Coq proof assistant, with operations such as insertion, deletion, and lookup. The goal is to ensure that all aforementioned operations adhere to the Red-Black Tree's balancing rules and invariant properties. My approach emphasizes both functional implementation and rigorous formal proofs of correctness.

Vision

The vision of this project started out as just implementing the lookup function and proving its correctness. As the project evolved, my goals shifted to include insertion and deletion fuctions and proofs about the efficiency of red-black trees using properties like the height, size, and black height of the tree.

Achievements

I have now completed the insertion and lookup functions (along with all helpers). I have implemented important lemmas as described here:

I have also completed the height, size, black height, and minimum allowable size functions that are used for proving efficiency of red-black trees.

Finally, I added the following functions to aid with the deletion of nodes from a red-black tree: blacken (convert tree root to black), check_no_red_red (check there are no parent-child red-red relations), check_balanced (check that the tree is balanced), check_red_black_invariant (uses aforementioned to check the red-black tree invariants), and balL and balR (left and right rotations to balance tree and recolor as necessary after deletion).

I added extensive unit test cases to aid in ensuring the correctness of my implementations.

Ultimately, I completed insert, delete, lookup, and some efficiency functions with rigorous proofs for the insertion and lookup functions.

Outcome Logic in Coq

Emmanuel J. Suárez Acevedo and Max Fan

Background

Program logics such as Hoare Logic are a useful tool for reasoning about the behavior of programs. For example, in Hoare Logic we can prove a Hoare triple {P} C {Q} indicating that given a precondition P is true, some postcondition Q will hold after executing the program C.

A Hoare triple can specify the correctness of the program. For example,

{y ≠ 0} z = div(x, y) {z is defined}

encodes that z will be defined as long as y is not equal to 0. If this triple is provable, then we've shown that our implementation of div is correct according to this specification.

What if we want to specify the incorrectness of the program instead (e.g. to know with certainty that the program has some bug)?

x = malloc(n)
*x = 1

Let's say we want to show that this program has a "bug" in the case that malloc fails and x is assigned to null. We might try proving the following Hoare triple specifying that the program will result in a "buggy" state:

{⊤} x = malloc(n) ; *x = 1 {*x fails}

However, in Hoare Logic our postcondition must be true for any execution of the program. We could only prove the above triple if malloc always failed. For this reason, we have to prove the following Hoare triple:

{⊤} x = malloc(n) ; *x = 1 {x ↦ 1 ∨ *x fails}

This triple appears to state that the program will either result in (1) x mapping to 1 or (2) a failure when x is dereferenced. However, the postcondition x ↦ 1 ∨ *x fails does not necessarily specify incorrectness: for any provable Hoare triple {P} C {Q} we can always prove {P} C {Q ∨ ⊥} -- even if C is correct!

That said, in practice we often find bugs in programs by showing their existence (e.g. through unit tests). For this reason, it would be nice to be able to reason about programs through their incorrectness. Recently, program logics such as Incorrectness Logic [incorrectness-logic] have been developed for this purpose.

In Incorrectness Logic, an incorrectness triple [P] C [Q] indicates that given precondition P, the postcondition Q will hold for some execution of the program C. Using an incorrectness triple, we can now encode the exact behavior we wanted to describe about the program before:

[⊤] x = malloc(n); *x = 1 [*x fails]      -- brackets instead of curly braces

Proving this triple now truly shows that the program has a bug -- there is some execution of the program that will result in a failure when dereferencing x.

However, because incorrectness logic underapproximates (the postcondition need only be true for some execution of the program) -- it is not suitable for proving the correctness of a program (which necessitates reasoning about all executions of a program).

Outcome Logic [outcome-logic] is a recent generalization of Hoare Logic that allows you to reason about both the correctness and incorrectness of a program.

The approach that Incorrectness Logic takes to reason about the existence of bugs in programs is to underapproximate (the postconditon need only be true for some execution of the program). However, the issue with Hoare Logic is not that it overapproximates but rather that it is not rich enough to talk about reachability: the logical disjunction P ∨ Q gives no guarantee that both P and Q are reachable.

On the other hand, Ouctome Logic is enriched with an outcome conjunction P ⊕ Q indicating that both the conditions P and Q are reachable. An outcome triple ⟨P⟩ C ⟨Q⟩ still indicates that Q is satisfied for any execution of the program as in Hoare Logic, but we can now specify both the correctness and incorrectness of the earlier example in a single triple:

⟨⊤⟩ x = malloc(n); *x = 1 ⟨x ↦ 1 ⊕ *x fails⟩        -- angle brackets

Proving this outcome triple not only shows that there is an execution of the program that is buggy -- it also shows that there is an execution of the program that is correct.

Outcome Logic still lets us talk about programs that are entirely correct (as the postcondition must be satisfied for any executiono of the program), and we can also still talk about a single bug in the program as in Incorrectness Logic. Instead of listing out every possible outcome, we can use the outcome conjunction with ⊤:

⟨⊤⟩ x = malloc(n); *x = 1 ⟨⊤ ⊕ *x fails⟩

Using the outcome conjunction with ⊤ underapproximates: it guarantees that there is a bug (as *x fails), but there may be other behaviors that are not covered (in the case that the trivial postcondition ⊤ is satisfied).

Project Summary

Introduction

Our project encodes outcome logic in Coq. Program logics have proven to be particularly useful in mechanized settings (e.g. the concurrent separation logic framework Iris [iris]). In addition to being monoidal (to reason about reachability of different outcomes), Outcome Logic is also monadic (to capture different computational effects). We believe Outcome Logic is a helpful program logic to encode in Coq to prove both correctness and incorrectness properties about programming languages with effectful properties, such as nondeterministim or probabilistic behavior.

Command Language

We work with a command language (CL) with nondeterministic branching and memory loads/stores. Here is the syntax in Coq:

Inductive cl : Type :=
| Zero                         (* sugared to 𝟘 *)
| One                          (* sugared to 𝟙 *)
| Seq : cl -> cl -> cl         (* sugared to ⨟ *)
| Branch : cl -> cl -> cl      (* sugared to + *)
| Star : cl -> cl              (* sugared to ⋆ *)
| Atom : cmd -> cl.

The command language encodes the flow of the program, whereas atomic commands actually perform memory loads/stores (as well as tests on expressions and assigning local variables). Here is the Coq syntax for atomic commands:

Inductive cmd : Type :=
| Assume : expr -> cmd              (* sugared to just 'e' *)
| Not : expr -> cmd                 (* sugared to ¬ e *)
| Assign : string -> expr -> cmd    (* sugared to x <- e *)
| Alloc : string -> cmd             (* sugared to x <- alloc *)
| Load : string -> expr -> cmd      (* sugared to x <- [ e ] *)
| Store : expr -> expr -> cmd.      (* sugared to [ e1 ] <- e2 *)

If we let x <- malloc just represent x <- alloc + x <- null, the previous malloc example can be written in Coq as:

Seq
  (Branch
    (Atom (Alloc x))
    (Atom (Assign x Null)))
  (Atom (Store (Var x) (Lit 1)))

With Coq notation, we can write it almost as we had it before:

  x <- malloc ⨟
  [ x ] <- 1

Semantics

We depart from the original Outcome Logic paper and use an operational, big-step semantics for the command language, with (C , σ) ⇓ σ' denoting that the program C evaluates the state σ to σ'. A state is either an error state (representing a memory error) or a stack (static memory) + heap (dynamic memory). Atomic commands modify the stack and heap, possibly resulting in an error state (in the case of a null pointer dereference).

Encoding outcome logic

Let ϕ, ψ range over outcome logic assertions ---- with P, Q instead ranging over atomic assertions (e.g. propositions). We say that an outcome triple ⟨ ϕ ⟩ C ⟨ ψ ⟩ is valid (denoted ⊨ ⟨ ϕ ⟩ C ⟨ ψ ⟩) if running the program on any state that satisfies the precondition results in a set of states that all satisfiy the postcondition. This is slightly different from the definition in the original Outcome Logic paper -- they generalize the definition over an arbitrary monad, while we fix our monad to the powerset monad. We do so to be able to prove concrete properties about nondeterministic programs (in particular, that our working malloc example can result in a trace that has a memory error).

We do not go over all of the assertions in outcome logic, instead we go over atomic assertions and the outcome logic assertion ϕ ⊕ ψ. We say that a set S satisfies this assertion (denoted S ⊨ ϕ ⊕ ψ) if S = S1 ∪ S2 and S1 ⊨ ϕ and S2 ⊨ ψ. Atomic assertions are those relating to a specific "outcome", e.g. x --> 1 (the pointer stored at x maps to 1 in the heap). A set satisfies an atomic assertion if it is a singleton set with a single state satisfying the outcome.

We also have an atomic assertion ok that is satisfied by any non-error state and an atomic asserion error satisfied by the error state.

Outcome Logic rules

We encode a set of rules (denoted ⊢ ⟨ ϕ ⟩ C ⟨ ψ ⟩ that can be used to derive the validity of an outcome triple. For example:

   ⊢ ⟨ phi ⟩ C1 ⟨ psi ⟩   ->   ⊢ ⟨ psi ⟩ C2 ⟨ theta ⟩ ->
  (* ------------------------------------------------ *)
              ⊢ ⟨ phi ⟩ C1 ⨟ C2 ⟨ theta ⟩

The first main result we prove is that these rules are sound:

if ⊢ ⟨ ϕ ⟩ C ⟨ ψ ⟩, then ⊨ ⟨ ϕ ⟩ C ⟨ ψ ⟩

Putting it all together

With our encoded OL rules, we are able to derive the OL triple:

  ⊢ ⟨ ok ⟩ x = malloc(n) ⨟ [ x ] = 1 ⟨ x --> 1 ⊕ error ⟩

By the soundness of our rules, we have⊨ ⟨ ok ⟩ x = malloc(n) ⨟ [ x ] = 1 ⟨ x --> 1 ⊕ error ⟩. The validity of this outcome triple means that if we run this program on any non-error state, one of our possible outcomes is an error.

Other properties of Outcome Logic

Our other main results are other properties about Outcome Logic itself. Following the original Outcome Logic paper, we define the semantic interpretation of an Outcome Logic assertion $\phi$ to be the set of models $\Phi \in 2^{M\Sigma}$ that satisfy the assertion. (Note that in our case $M\Sigma=2^{\Sigma}$).

A semantic outcome logic triple is then defined as follows: $$ \vDash_S \langle \Phi \rangle\,C\,\langle \Psi \rangle \text{ iff } \forall m \in M\Sigma, m \in \Psi \implies [[C]] (m) \in \Psi $$

With these definitions, we proved the following theorems from the Outcome Logic paper:

These theorems together let us prove principle of denial, which states that if there is a syntatic assertion $\phi'$, $\phi'$ is satisfiable, and the syntactic triple $\langle \phi' \rangle\,C\,\langle \lnot \psi \rangle$ holds, then the syntactic triple $\langle \phi \rangle\,C\,\langle \psi \rangle$ does not hold for any weaker precondition $\phi$ (that is, $\phi' \implies \phi$).

Conclusion

We have encoded an instance of outcome logic in Coq and used it prove the (in)correctness of nondeterministic programs with dynamic memory. We have additionally mechanized in Coq properties about Outcome Logic shown in the original Outcome Logic paper. As future work, we would like to 1) generalize this framework to an arbitrary monad to make it more reusable, explore other instantiations of outcomne logic (e.g. to prove properties about probabilistic programs), and 3) use Coq to explore extensions to outcome logic, such as relational outcome logic.

References

[iris]: Ralf Jung, David Swasey, Filip Sieczkowski, Kasper Svendsen, Aaron Turon, Lars Birkedal, and Derek Dreyer. 2015. Iris: Monoids and Invariants as an Orthogonal Basis for Concurrent Reasoning. In POPL. 637–650. https://doi.org/10.1145/2676726.2676980

[incorrectness-logic]: Peter W. O’Hearn. 2019. Incorrectness Logic. Proc. ACM Program. Lang. 4, POPL, Article 10 (Dec. 2019), 32 pages. https://doi.org/10.1145/3371078

[outcome-logic]: Noam Zilberstein, Derek Dreyer, and Alexandra Silva. 2023. Outcome Logic: A Unifying Foundation for Correctness and Incorrectness Reasoning. Proc. ACM Program. Lang. 7, OOPSLA1, Article 93 (April 2023), 29 pages. https://doi.org/10.1145/3586045

[caveat]: We interpret a semantic triple to not hold as constructively meaning that there exists a countermodel that falsifies the triple.

Verifying Brzozowski and Antimirov Derivatives

Ernest Ng and Laura Zielinski

Introduction

Derivatives of regular expressions are an elegant and algebraic technique, beloved by functional programmers, for implementing regex matching.

The technique originated from Janusz Brzozowski (1962). Brzozowski's insight was that given a regex $r$ and the first character $c$ in the input string, the derivative of $r$ with respect to $c$, denoted $\delta_c(r)$, is another regex which matches the remainder of the string. Now, suppose we iteratively compute derivatives for each character in the string $s$. If the final regex accepts the empty string $\epsilon$, then $s$ must have matched the original regex $r$! Brzozowski derivatives can be implemented pretty easily in functional languages, as shown in this blogpost by Harry Goldstein.

In 1995, Valentin Antimirov introduced an alternative to Brzozowski's method using partial derivatives. A partial derivative of $r$ with respect to $c$ is a regex $r'$ such that if $r'$ accepts a string $s$, then $r$ accepts $c\cdot s$. The Antimirov derivative of $r$ with respect to $c$, denoted $\alpha_c(r)$, is a set of partial derivatives. The idea is that the Antimirov derivative should collectively accept the same strings as the Brzozowski derivative. Antimirov derivatives also lend themselves to a concise implementation, as Neel Krishnaswami shows in this blogpost.

Moreover, we explored some recent results published in Romain Edelmann's PhD dissertation from EPFL. In his thesis, Edelmann shows how Brzozowski derivatives can be implemented using a purely functional data structure called a zipper), which is used to navigate tree-shaped datatypes (e.g. our regex AST). A zipper consists of a focused subtree $t$ and a context, which contains the path taken to reach $t$ along with $t$'s siblings. Here's an illustration:

(Diagram inspired by Darragh & Adams's ICFP '20 talk)

When navigating through our regex AST, we can shift the zipper's focus to a different subtree, which creates a new zipper with an updated context. Edelmann demonstrates in his dissertation that Brzozowski derivatives can be computed using zippers! His idea was to move the zipper's focus and update the context every time the Brzozowski derivative function $\delta_c$ makes a recursive call, with multiple recursive calls corresponding to multiple focuses.

Edelmann's insight was that the Brzozowski derivative only introduces 2 new kinds of AST constructors, namely $+$ and $\cdot$. Edelmann demonstrates how we can use sets and lists respectively to represent these two operations:

Now, Edelmann mentions in passing that his zipper representation is "reminiscent of Antimirov derivatives." We formally proved Edelmann's observation, i.e. that the set of terms contained within a Brzozowski zipper is the same as the set of terms contained in the set of Antimirov derivatives (modulo some rewrite rules).

In this project, we mechanize proofs that relate the two notions of derivatives and the zipper representation of Brzozowski derivatives.

  1. Regex matchers based on Brzozowski and Antimirov derivatives are equivalent, in that they accept exactly the same set of strings. They are also equivalent to an inductively-defined matcher.
  2. There are finitely many Antimirov partial derivatives for a given regex. (This means that we can write an algorithm to build a DFA using these derivatives.)

  3. Michael Greenberg has a blogpost in which he investigates how the size of a regex grows as we take successive Brzozowski derivatives. In particular, the size (number of AST nodes) of Brzozowski derivatives grows exponentially, and the height (of the AST representation) of a Brzozowski derivative is at most twice the height of the original regex. We proved similar results for the Antimirov derivative:

    a. The height of an Antimirov partial derivative is at most twice the height of the original regex.

    b. The number of Antimirov partial deriatives of a regex is linear in the AST size of the original regex.

  4. If we concatenate the elements within each context (list of regexes) contained in Edelmann’s zipper, we get the same set of regexes as the Antimirov derivative.

Thus, we have proved notions of equivalence for Brzozowski-based matchers, Antimirov-based matchers, and the zipper representation of the Brzozowski derivative. We also proved bounds on size, height, and finitude for these derivatives. Finally, we also implemented much of our work in OCaml to allow these derivative-based matchers to be executed. Our code is available on GitHub.

Verifying Distributed Consensus Algorithms

Gerardo Garcia Teruel Noriega

Introduction

Distributed systems are everywhere today, well established protocols like 2PC and Paxos are foundational building blocks of distribued databases like DynamoDB and Cloud Spanner. Most of these foundations were established by researchers from the 1970s to the 2000s, like Lamport, Hadzilacos, Toueg, Skeen, among many others; and their liveness and correctness properties demonstrated using high level pseudocode and pen and paper proofs. Recently, there's been work in the development of frameworks that would allow the development and verification of Distributed Algorithms with extraction and optimization tools to even optimize them (Verdi, Grove). My goal was instead to describe some interesting algorithms in Coq and prove them correct using the Coq Proof Assistant, similar to an Imp version of a language for distributed systems, and with a focus on consensus protocols.

What's a distributed system anyway?

The basic idea in a distributed system is that an arbitrary number of processors work independently to achieve a task, the processors only have local information and might not know about the state of other processors. They are able to synchronize and achieve a task together by sending and receiving messages that they then use to change their internal state. One of the key problems of distributed systems is that of agreement: let's say that every process is interested in writing a value for a single-write register. 

Some processes with unique identifiers, they agre on the decision function and on the number of processes participating at initialization.

Process 1:
    pid: 1
    value-to-propose: 10
    decisionFunction: min
    n: 2

Process 2:
    pid: 2
    value-to-propose: 20
    decisionFunction: min
    n: 2

A simple solution would be for everyone to send their proposals and to wait to receive messages from every other process: 

Definition start(p: Process): (Process, list Message) :=
    (p, sendAll p n)

Definition sendAll(p: Process)(n: nat): list Message :=
match n with
| 0 => []
| S n' => (n, proposal p) :: (sendAll p n')

Definition receive(m: Message)(p: Process) :=
    let p' := handle p m in
    if (Nat.eqb (length (seen p')) n)
    then halt p'
    else p'

Some key aspects to mention:

Let's start by tacking the message delivery issue first, we can use process algebras or rely on a message buffer.

Process Algebras

A simple process algebra would have processes with two states: receive and send. Whenever these two states match, the message is exchanged between the processes and the system as a whole continues to make progress:

Inductive ProcessState :=
(* to, proposal*)
| Send nat nat
| Receiving
.

Definition next(p1 p2: Process): (Process * Process) :=
match (state p1, state p2) with
| (Send to m, Receiving) => if (Nat.eqb to (pid p2)) then (step p1, handle p2 m)
| (Receiving, Send to m) => if (Nat.eqb to (pid p1)) then (handle p1 m, step p2)
| _ => (p1, p2)
.

This abstraction is quite powerful but would rely on processes being in matching states for the system to make progress without deadlocking, let's consider instead an option with message buffers.

Message Buffers

In a message buffer approach, all messages are posted to a buffer and are later delivered to the appropriate messages. Buffers are powerful as they allow us to reason about systems with different delivery guarantees (i.e. are messages delivered in FIFO or arbitrary order? can they be lost or duplicated? ). Many systems model buffers close to the network in which if processes are connected via a wire they are connected with a channel (different topologies can arise depending on the number of channels in the system). But instead, let's focus on having a single message buffer were all messages are posted, we'll see the power of this abstraction in a second. 

Definition pid := nat.
Definition message := nat.
(* from, to, message *)
Definition MB := list (pid * pid * Message).

Definition next (p: Process)(mb: MB): (Process * MB) :=
match (pstate p) with
| Sending to m => (step p, mb ++ [((pid p), to, m)])
| SendAll m => mb ++ (allMessages (n p) (pid p) m)
| _ => _
.

Fixpoint allMessages(n: nat)(from: pid)(m: Message) : list Message :=
match n with
| 0 => []
| S n' => (from, n, m) :; (allMessages n' from m)

Definition ableToReceive(p: Process)(m: Message): bool :=
    andb (Nat.eqb (pid p) (to m)) (pstate p = Idle).

Definition next(mb: MB)(p: Process): (MB * Process) :=
match mb with
| [] => (mb, p)
| (from, to, m) :: t => if ableToReceive p m then (step p m, t) else (p, mb)
end.

Okay so this definition gives us a bit more flexibility as processes are able to complete the message sending without having to wait for a process to be in a receiving state. At the cost of some more complexity to manage in the transition rules. Let's keep this model and move to an arbitrary number of processes and we'll get back to it for our first consensus protocol.

Arbitrary number of participants

So far i've only talked about processes having a small amount of participants, what about modelling an arbitrary number of processes? There can be multiple design decisions but what I found simplest was to just say that processes are modeled by natural numbers (their pid) and that there is a function that maps pids to a Process state: 

Inductive PState := 
| Initial
| Idle
| Send to m
| Halt
.

Definition pid := nat.
Definition Processes := pid -> PState.
(* All values seen by a process *)
Definition seen := pid -> list nat. 
(* The initial value that a system proposes. *)
Definition proposal := pid -> nat.

(* Shallow embedding here on how a process changes state. Contains both state change and halting.*)
Definition handle (p: Process)(s: seen)(ps: Processes)(m : Message): (seen, Processes) := 
    let s' := fun x => if (Nat.eqb x (pid p)) 
        then s x ++ [m.thd]
        else s x
    in
    let ps' := fun x =>
        if (andb (Nat.eqb x (pid p)) (Nat.eqb n (length (s' x)))) 
        then Halt
        else ps x in
    (s', ps')

Putting this altogether, we can use an inductive relation to model transitions in the state and show with an example that the algorithm works.

Inductive Step : N -> Processes -> proposal -> seen -> MB -> Prop :=
(* A state is a failed one if processes haven't completed and there are no pending messages *)
(* This means that no process can make any more progress. *)
| Done: 
forall (n: nat) (mb: MB) (ps: pstates) (s: seen) (v0s: proposal),
    mb = []
    -> (n > 1 -> forall (p1 p2: pid), p1 < n /\ p2 < n /\ p1 <> p2 -> s p1 = s p2)
    -> forall (p: pid), p <= n -> ps p = Halt
    -> Step n ps v0s s mb
(* 
A deterministic attempt. Every process sends a message in increasing pid order.
The message buffer is full with all proposals.
*)
| NextSend : forall (n: nat) (mb mb': MB) (ps ps': pstates)(s: seen)(v0s: proposal),
    mb' = start n 0 (v0s)
    -> ps' = (fun x => Idle)
    -> mb = []
    -> Step n ps' v0s s mb'
    -> Step n ps v0s s mb
(* 
Processes the messages in the message buffer one at a time. 
The head message is processed by its respective queue.
 *)
| NextReceive :
    forall (n : nat) (mb mb': MB) (ps: pstates)(s s': seen)(v0s: proposal),
    mb <> []
    -> (mb', s') = receive mb s
    -> Step n ps v0s s mb'
    -> Step n ps v0s s mb
.

Our relation here shows that every process will see the same number of values, not that they all decide on the same value which is a slightly different definition of consensus. 

(* a simple example with three process were every process proposes its pid. *)
Example agreement_example : Step 3 (fun x => Initial) (fun x => x) (fun x => []) [].
Proof.
    eapply NextSend; eauto.
    eexists.
    simpl.

    (*
    message buffer will contain all 9 messages. 
    *)
    eapply NextReceive; try unfold sendAll; try simpl; auto; try congruence.
    eapply NextReceive; try unfold sendAll; try simpl; auto; try congruence.
    eapply NextReceive; try unfold sendAll; try simpl; auto; try congruence.
    eapply NextReceive; try unfold sendAll; try simpl; auto; try congruence.
    eapply NextReceive; try unfold sendAll; try simpl; auto; try congruence.
    eapply NextReceive; try unfold sendAll; try simpl; auto; try congruence.
    eapply NextReceive; try unfold sendAll; try simpl; auto; try congruence.
    eapply NextReceive; try unfold sendAll; try simpl; auto; try congruence.
    eapply NextReceive; try unfold sendAll; try simpl; auto; try congruence.


    eapply Done.
    reflexivity.
    auto.
    eauto.
    eauto.
Qed.

Non determinism

Okay so we now are confident that the algorithm works on an ideal setting, but this relies on a deterministic execution. But what about messages received in any order? Well here, I relied on a trick to avoid adding too much complexity to the inductive relation, instead I relied on Coq's permutation library: 

Lemma agreement_permutation: forall n ps p s mb1 mb2, 
    Permutation mb1 mb2 -> Step n ps p s mb1 -> Step n ps p s mb2.

Where instead we can rely on structural induction to show that if a run with a certain message buffer holds, then that relationship holds for any permutation of the message buffer. This approach might not hold for majority-based protocols (as one execution and another might lead to different decisions based on the accepting majority), but allows us to make progress for now.

Failures.

An interesting aspect to consider is how can we improve our algorithm to tolerate an arbitrary number (f) of failures. We have two options:

Synchrony with crash failures.

The nitty gritty of how to model synchronous systems can get tricky as the formalism relies on an upper bound of message processing time, message sending time, and message receiving time. Instead i'll move this complexity into the semantics of the transition and think about this as a kind of "divine synchrony".

Image that all processes receive messages, and one of the message that they receive is the round in which they are currently a participant. The round number is sent by a ~god~ coordinator and will only deliver the next round if all the messages for the current round have been processed already.

We'll update the Pstate to handle these rounds appropriately. 

Inductive PState := 
| Initial
| Idle (r: nat)
| Halt
.

Definition pid := nat.
Definition Processes := pid -> PState.
(* All values seen by a process *)
Definition seen := pid -> list nat. 
(* The initial value that a system proposes. *)
Definition proposal := pid -> nat.

Inductive Step : N -> Processes -> proposal -> seen -> MB -> Prop :=
(* A state is a failed one if processes haven't completed and there are no pending messages *)
(* This means that no process can make any more progress. *)
| Done: 
forall (n: nat) (mb: MB) (ps: pstates) (s: seen) (v0s: proposal),
    mb = []
    -> (n > 1 -> forall (p1 p2: pid), p1 < n /\ p2 < n /\ p1 <> p2 -> s p1 = s p2)
    -> forall (p: pid), p <= n -> ps p = Halt
    -> Step n ps v0s s mb
| NextStart : forall (n: nat) (mb mb': MB) (ps ps': pstates)(s: seen)(v0s: proposal),
    mb' = start n 0 (v0s)
    -> ps' = (fun x => Idle 0)
    -> mb = []
    -> Step n ps' v0s s mb'
    -> Step n ps v0s s mb
| NextRound : forall (r: nat)(n: nat) (mb mb': MB) (ps ps': pstates)(s: seen)(v0s: proposal),
    mb' = round n (S r) (v0s)
    -> ps' = (fun x => Idle r)
    -> mb = []
    -> Step n ps' v0s s mb'
    -> Step n ps v0s s mb
(* 
Processes the messages in the message buffer one at a time. 
The head message is processed by its respective queue.
 *)
| NextReceive :
    forall (n : nat) (mb mb': MB) (ps: pstates)(s s': seen)(v0s: proposal),
    mb <> []
    -> (mb', s') = receive mb s
    -> Step n ps v0s s mb'
    -> Step n ps v0s s mb
.

And our shallow embedding becomes quite straightforward: 

Definition round(n: nat)(f: nat)(r: nat)(p: pid)(s: SynchSeenValues)(v0s: SynchProposals)(ps: SynchProcesses): (SynchProcesses * SynchSeenValues * SynchMB) :=
match r with
| 0 => 
    (* Initialization, add initial proposal to seen values. *)
    let s' := fun p' => if (Nat.eqb p p') then [(v0s p')] else s p' in
    (* message sending *)
    let mb' := synchSendAll n r p s' in
    (ps, s', mb')
| _ => 
    (* for now only message sending *)
    let mb' := synchSendAll n r p s in
    if (Nat.leb r (S f))
    (* rth round starts *)
    then (ps, s, mb')
    (* last round - no more message sending *)
    else 
    let ps' := fun x => if (Nat.eqb x pid) then Halt else ps x in
    (ps' s, [])
end.

But now the transition steps become more complicated as we need to allow each process to either crash before sending an arbitrary number of messages. The expansion grows quite quickly, but modelling this as a programming language allows us to make some progress: 

Inductive PState := 
| Initial
| Run (r: nat) (c: Cmd)
| Crash
| Halt
.

Inductive Cmd :=
| SendSeq: list (pid * pid * Message)
| Idle
.

This setup allows more flexibility for our setup:

What's next?

The original paper of FLP used a non-constructive proof, so it's not easy to translate to Coq. But there are a couple of constructive proofs available that are translatable. I'm hoping to translate Robert Constable's proof to Coq to do this.

Finally, non terminating protocols are difficult to model in Coq, but some we cna get around it in a few different ways. For now, i'm exploring continuation trees to model a non-terminating consensus protocol.

Secure Declassification

Goktug Saatcioglu

Motivation

Information flow labels have been used to enforce security policies that prohibit the transfer of information from secret data to public data. However, these security policies are often too conservative for real-world applications, because most programs must selectively declassify certain secret data. For example, a voting program

$$w:=maj(v_1,v_2,v_3)$$

that inputs three votes $$v_1$$, $$v_2$$ and $$v_3$$ and stores the majority in variable $$w$$ using the majority function $$maj(\cdot)$$ would ensure the confidentiality of individual votes by labelling each vote secret1, secret2 and secret3 respectively.

To ensure confidentiality of variables that appear in the right-hand side of an assignment, the label for the left-hand side must be marked at least as restrictive as the labels that appear on the right-hand side. This rule implies that the labels can only get more restrictive as a computation proceeds. In the voting program above, the label for $$w$$ must be at least as restrictive as the labels on the arguments to $$maj(\cdot)$$, meaning $$w$$ must be labelled at least as secret as $$v_1$$, $$v_2$$ and $$v_3$$ . To be at least as restrictive as the labels on each individual vote, $$w$$ must have a label that no principal can read, such as top_secret. However, this label for $$w$$ is undesirable; an election where participants cannot learn the result is not useful.

A way to programatically convert the label on $$w$$ from being too restrictive to less restrictive is needed. Such a mechanism would perform a reclassification of labels. In the case of the voting program, this reclassification would be characterized as declassification. Current approaches to declassification introduce escape hatches for changing the label of a variable, but they do not require an assurance argument that the declassification would not cause too much information to be leaked to an observer.

For example, in the voting program, a simple analysis reveals that if $$v_1$$ votes for one candidate while $$v_2$$ and $$v_3$$ vote for another candidate then a principal that can learn the value of $$v_1$$ can deduce the values of $$v_2$$ and $$v_3$$ from knowledge of majority $$w$$. So, in certain scenarios votes cast by participants are not kept secret.

On the other hand, in the voting program if there are $$5$$ voters then we know that regardless of the knowledge of vote $$v_1$$ and majority $$w$$ any one voter, such as $$v_2$$, could have voted for any candidate. That is, for any value of $$v_1$$ and $$w$$ and candidate $$c$$, there exists an assignment of votes such that this assignment also produces the same values of $$v_1$$ and $$w$$ and $$v_2$$ holds the value $$c$$.

More generally, a declassification is safe if any value is plausible for a vote $$v_i$$ given fixed values for the majority, stored in $$w$$, and a vote $$v_j$$ with $$i\ne j$$ that an observer can learn. Plausible means that it is possible to compute $$w$$ using the votes under analysis. Enumerating all possible $$w$$ and $$v_j$$ reveals that in the $$3$$-voter example when $$v_j\ne w$$ then $$v_i$$ must be equal to $$w$$, meaning it is not plausible that $$v_i$$ have any value and in the $$\ge5$$-voter example is it plausible for $$v_i$$ to have any value. For the $$3$$-voter case, $$v_i$$ must give a specific candidate which an observer can deduce by knowing the values of $$w$$ and $$v_j$$ and for the $$\ge5$$-voter case $$v_i$$ cannot be determined to be a single value as a function of $$w$$ and $$v_j$$. By this analysis, the $$3$$-voter and $$4$$-voter cases of voting program violate the security policy and the $$\ge5$$-voter cases satisfy the security policy. Our security policy captures the intuition behind this informal analysis as a $$\forall\exists$$-hyperproperty.

Project Overview

Our project for CS6115 formalizes a proof system for verification of programs written in an IMP-like programming language with explicit declassification statements that can be used to verify whether programs satisfy our security policy hyperproperty. To this end, we have built the following components in Coq:

  1. Formalization of our IMP-like language.
  2. The small step operational semantics and the trace semantics of our language.
  3. A security type system for this language (inspired by other type systems for information flow control, specifically the RIF system that enforces piecewise non-interference).
  4. The non-interference and attacker observation properties of programs that are type correct with respect to the type system in bullet 3.
  5. The semantics of the proposed proof system. This proof system is a Hoare-like logic that has the same semantics of under-approximate Hoare logics such as Reverse Hoare Logic (RHL) and Incorrectness Logic (IL) but is parameterized over the typing context that certifies a program is type correct and a security label associated with a principal's observation capability.
  6. Two theorems that show that if the security policy holds for states that satisfy a post-condition determined by the proof system from 5 then the security policy holds for the traces of the program. Hence, we reduce the relational verification problem to a non-relational one.
  7. Running examples demonstrating the use of the proof system to show that the security policy does not hold for the $$3$$-voting case and to verify that security policy is satisfed for the $$5$$-voting case.

Explaining the theory and proofs of this work would involve converting an entire work-in-progress research project to a blog post. Instead, we present some interesting results and technical achievements.

Some Details

$$\lambda$$-equivalence of states

An information-flow type system assigns labels $$\lambda\in\mathcal{L}$$ to variables $x,y,z\dots\in Var$ where $$(\mathcal{L},\sqsubseteq,\sqcup,\sqcap)$$ forms a complete lattice. A labelling scheme is usually defined using a labelling function $$\Gamma\in Var\to\mathcal{L}$$. Given $$\Gamma$$, it is possible to define a $$\lambda$$-projection (or view) of a state $$s\in Var\to\mathbb{N}$$ as follows

$$s_{\downarrow\lambda}={v\mapsto s(v):v\in Var\land \Gamma(v)\sqsubseteq\lambda}$$

such that $$s_{\downarrow\lambda}$$ is a restriction of the mapping $$s$$ where the domain of $$s$$ is restricted to only variables that have label less than or equal to $$\lambda$$. Two states are said to be $$\lambda$$-equivalent if their $$\lambda$$-projections are the same state:

$$s_1\sim_{\lambda}s_2\iff (s_1){\downarrow\lambda}=(s_2){\downarrow\lambda}.$$

Our first goal was to model $$\lambda$$-equivalence of states in Coq. Since states are total functions the $$\lambda$$-projection definition above is not well defined in Coq. In fact, according to our definitions so far, the $$\lambda$$-projection of a state does not produce another state. Thus, to overcome this issue we side step the definition of $$\lambda$$-projection and define $$\lambda$$-equivalence of states as follows:

$$s_1\sim_{\lambda}s_2\iff\forall (v:Var),\Gamma(v)\sqsubseteq\lambda\implies s_1(v)=s_2(v).$$

It should be clear that this definition of $$\lambda$$-equivalence corresponds to our initial notion $$\lambda$$-equivalence with the added benefit that this definition can be used in Coq to start formalizing other information flow notions and theorems.

$$\lambda$$-equivalence of traces

In information flow we are more concerned with program traces rather than single states of a program. So, we wish to lift the definition of $$\lambda$$-equivalence from the previous section to traces. For this research a trace $$\pi$$ is a finite sequence of states $$s_1s_2\dots s_n$$ where $$n$$ is the length of $$\pi$$ and $$\pi[i]$$ indexes state $$0<i\le n$$ of $$\pi$$. We denote the empty sequence with $$\epsilon$$.

A general strategy to define $$\lambda$$-equivalence of traces is to first define a $$\lambda$$-projection of traces and then compare two $$\lambda$$-projections to obtain the equivalence relation. One possible definition of $$\lambda$$-projection is as follows:

$$\pi_{\downarrow\lambda}=\begin{cases}\epsilon& \pi=\epsilon\\s & \pi=s\\(s_2\pi')_{\downarrow\lambda} & \pi=s_1s_2\pi'\land s_1\sim_{\lambda}s_2\\s_1(s_2\pi')_{\downarrow\lambda}&\pi=s_1s_2\pi'\land s_1\not{\sim_{\lambda}}s_2\end{cases}.$$

This definition deletes consecutive $$\lambda$$-equivalent states from a trace such that every state in the resulting projection trace is distinct from each other by at least one variable that has label less than or equal to $$\lambda$$. The projected trace corresponds to the view an attacker who can only inspect the values of variables with label less than or equal to $$\lambda$$ may have of a system's execution where the attacker can only observe updates to variables and cannot count the number of execution steps. Using this definition of projection it is straightforward to define $$\lambda$$-equivalence:

$$\pi_1\sim_{\lambda}\pi_2\iff \forall i,(\pi_1[i]) {\downarrow\lambda}=(\pi_2[i]) {\downarrow\lambda}.$$

Note that this definition necessitates that $$\pi_1$$ and $$\pi_2$$ to be of the same length if they are to be $$\lambda$$-equivalent.

We wish to translate these definitions into Coq. The first task is to formalize $$\lambda$$-projection in Coq. The definition of $$\lambda$$-projection relies on the definition of $$\lambda$$-equivalence of states which in Coq is a comparison between arbitrary functions and hence not decidable. So, modelling $$\lambda$$-projections as a fixpoint definition is not possible (or at least quite difficult to do and work with). Instead, the $$\lambda$$-projection of a trace is modelled as an inductive relation that corresponds to taking a single step in a fold computation. Our relation is of the form

$$(\pi,acc)\downarrow_{\lambda}(\pi',acc')$$

where $$\pi$$ is the trace we are projecting currently, $$acc$$ is the projection we have built so far (the accumulated trace), $$\pi'$$ is what remains to be processed after $$\pi$$ is processed and $$acc'$$ is the projection after the processing of $$\pi$$. This relation consists of three rules:

  1. $$\frac{}{(s::\epsilon,acc)\downarrow_{\lambda}(\epsilon,acc@[s])}$$
  2. $$\frac{s_1\sim_{\lambda}s_2}{(s_1::s_2::\pi,acc)\downarrow_{\lambda}(s_2::\pi,acc)}$$
  3. $$\frac{s_1\not{\sim_{\lambda}}s_2}{(s_1::s_2::\pi,acc)\downarrow_{\lambda}(s_2::\pi,acc@[s_1])}$$

where $$@$$ is the append operation.

Letting $$\downarrow_{\lambda}^*$$ be the reflexive transitive closure of $$\downarrow_{\lambda}$$ lets us take multiple steps of this fold computation. Hence, the $$\lambda$$-projection of trace $$\pi$$ is $$\pi'$$ whenever we have $$(\pi,\epsilon)\downarrow_{\lambda}^*(\epsilon,\pi')$$. That is, if we consume the entirety of $$\pi$$ under the $$\downarrow_{\lambda}^*$$ relation than the accumulated result $$\pi'$$ is the $$\lambda$$-projection of $$\pi$$.

Continuing the theme of reflexive transitive closures of inductive relations as fold operations, we can define the $$\lambda$$-comparison of two traces using the relation

$$\frac{s_1\sim_{\lambda}s_2}{(s_1::\pi_1,s_2::\pi_2)\cong_{\lambda}(\pi_1,\pi_2)}$$

and take the reflexive transitive closure of $$\cong_{\lambda}$$, denoted $$\cong_{\lambda}^*$$. If $$(\pi_1,\pi_2)\cong_{\lambda}(\epsilon,\epsilon)$$ holds, so as to consume traces $$\pi_1$$ and $$\pi_2$$ entirely, we have that the two traces are step-wise equivalent.

Bringing everything together, two traces $$\pi_1$$ and $$\pi_2$$ are $$\lambda$$-equivalent if and only if

  1. $$(\pi_1,\epsilon)\downarrow_{\lambda}^*(\epsilon,\pi_1')$$,
  2. $$(\pi_2,\epsilon)\downarrow_{\lambda}^*(\epsilon,\pi_2')$$,
  3. $$(\pi_1,\pi_2)\cong_{\lambda}^*(\epsilon,\epsilon)$$.

This formalization of $$\lambda$$-equivalence of traces lets us model other information flow notions and facts known from the literature and prove them in our project. Furthermore, we can then use these facts to help with the proofs of Theorem 1 and Theorem 2.

Trace Semantics of Reverse Hoare Logic

Under-approximate Hoare-like logics such as Reverse Hoare Logic (RHL) and Incorrectness Logic (IL) provide the guarantee that any state that satisfies the post-condition of a triple is a reachable, i.e., realizable, state of the program. This notion is semantically captured by the validity condition

$$[P]c[Q]\iff\forall s',s'\vDash Q\implies\exists s:s\vDash P\land(s,c)\rightarrow^*(s',Skip)$$

where $$c$$ is a program and $$\rightarrow^*$$ is the reflexive transitive closure of the small-step relation $$\rightarrow$$, that is $$\rightarrow^*$$ corresponds to taking an arbitrary amount of small steps.

For our research and this project we provide a trace semantics for RHL. To do this we begin by providing a small step operational trace semantics that is parameterized over a small step operational (state) semantics of a programming langauge. Let $$(s,c)\rightarrow_{\Sigma}(s',c')$$ be the small step operational (state) relation of some programming language. Then, define

$$\frac{(s,c)\rightarrow_{\Sigma}(s',c')}{(s::s'::\pi,c)\rightarrow_{\Pi}(s'::\pi,c')$$

as the relation that gives a trace semantics to this language. The relation $$\rightarrow_{\Pi}$$ builds traces in reverse order. In other words, the trace semantics of a program is built by consuming elements of a trace. As long as a step can be taken in the state small step semantics of a program the trace semantics can continue consuming elements of a trace.

Let $$\rightarrow_{\Sigma}^*$$ be the reflexive transitive closure of $$\rightarrow_{\Sigma}$$ and $$\rightarrow_{\Pi}^*$$ the reflexive transitive closure of $$\rightarrow_{\Pi}$$. Then, we proved in Coq the following statement

$$(s,c)\rightarrow_{\Sigma}^*(s',c')\iff\exists\pi:\pi',\pi[1]=s\land\pi'[1]=s'\land(\pi,c)\rightarrow_{\Pi}^*(\pi',c')$$

such that there is an intuitive correspondence between the state and trace semantics of this language. Namely, if the program with initial state can step some amounts of time to produce a new state then there is a trace that corresponds to that execution. Note that we need to existentially quantify over two traces because the program may continue executing after reaching the point $$(s',c')$$ so the second trace $$\pi'$$ represent a possibly continuing computation. Furthermore, this statement is a bit weak in the sense that we actually know that $$\pi'$$ is a suffix of $$\pi$$ since computations are deterministic. However, for this project we did not need to prove this fact and so this part of the correspondence between the trace and state semantics is not shown.

As a special case of the above statement we get the following correspondence between terminating state and trace executions

$$(s,c)\rightarrow_{\Sigma}^*(s',Skip)\iff\exists\pi,\pi[1]=s\land(\pi,c)\rightarrow_{\Pi}^*([s'],Skip)$$

which in turns lets us derive a trace semantics for RHL triples

$$[P]c[Q]\iff\forall s'\vDash Q\implies\exists\pi,\pi[1]\vDash P\land(\pi,c)\rightarrow_{\Pi}^*([s'],Skip)$$

which is a more formal way of expressing the intuitive notion that every post-condition state of an RHL triple is realizable by some execution of the program where the initial state of that execution satisfies the pre-condition. There could be ways to enrich this semantics to talk about history (and possibly prophecy) in RHL triples which might serve as interesting research projects in the future. For this project, the above trace semantics of RHL triples are used to design a proof system for secure declassification.

Summary

The above technical achievements were crucial in building the proof system mentioned in the introduction and to prove interesting semantic properties of this system in the forms of Theorem 1 and Theorem 2. We hope to publish my work soon where this course project will serve as an artifact to accompany the paper. More details will (hopefully) be available soon!

Acknowledgments

This work is based on joint work with Fred B. Schneider.

Formally Verifying Operational Semantics In Packet Scheduling

Kabir Samsi

Introduction

Packet Scheduling is a branch of network design which involves sequencing how packets of data are processed. Programmable Packet Scheduling adds a layer of customizability and programmability to this, and motivates an intersection of programming language theory and network design. Programmers interested in controlling packet scheduling typically express policies, rules which determine how queues of packets are processed. This project formalizes *Rio, *a programming language targeted towards expressing policies, defines a semantics for it, and proceeds to provide formalisms both on the semantics and the underlying queues.

My project focused on verifying several aspects of the semantics of the language, and using the semantics to prove a handful of optimizations for the language. This included firstly formalizing a series of signatures for lists, forming underlying queues of packets, and semantics of the language, and proving fundamental characteristics of the system here. These included showing how repeated unions of underlying class definitions could be removed; analyzing how different policy transformers interact, and showing equivalence of small programs in the form of ASTs.

Formalisms Over A List Module

Lists serve as the representation for queues in the semantics. A central part of the semantics involves sorting queues of packets to prioritize packets with higher rank, weight, etc. and scheduling those packets to be popped first. As a result, the nexus of this portion of the project was formalizing a variant of the insertion-sort algorithm in Coq, and formally proving its correctness by creating a definition for sortedness.

A first step in this process is to develop a handful of straightforward list operations in Coq. One can then also develop a definition for sortedness:

(* Verifies that a list of packets is sorted (with fuel). *)
Fixpoint sorted_aux {A : Type} (len : nat) (q : list A) (f : A -> nat) : bool :=
    match len with
    | 0 => true
    | S len' =>
        match q with
        | [] => true
        | h :: [] => true
        | h1 :: h2 :: t => 
            andb (Nat.leb (f h1) (f h2))
            (sorted_aux len' (h2 :: t) f)
        end
    end.


(*  Verifies that a list of packets is sorted
    with a given function mapping packets to nats. *)
Definition sorted {A : Type} (q : list A) (f : A -> nat) : bool :=
    sorted_aux (length q) q f.

Here, one has to be careful to construct well-formed, terminating recursion. This definition can then be used with a (correct) sorting algorithm to set up the following lemma:

Theorem sorting_works : forall {A : Type} (q : list A) (f : A -> nat),
    sorted (sort q f) f = true.

Beyond this, the list interface involved developing a handful of definitions and lemmas over list partitioning, preservation of sortedness, and more.

Formalising Packets and Queues in Coq

Packets are collections of data which have characteristics that policies can use to determine how they should be processed. Formally (in the scope of this project), I define them as a triple of nats (rank, time, weight) whose attributes can be accessed and then used to sort, prioritize and operate over queues containing them.

Definition packet := (nat * nat * nat)%type.

Definition rank (pkt : packet) := match pkt with
| (r, _, _) => r
end.

Definition time (pkt : packet) := match pkt with
| (_, t, _) => t
end.

Definition weight (pkt : packet) := match pkt with
| (_, _, w) => w
end.

Queues are treated as lists, prone to sorting, partitioning, and having their heads and tails accessed. Queues become one of the two major parts of the semantics, alongside the Rio AST.

Formalising Semantics in Coq

The Rio language can be thought of as follows: 1) Classes, dictating sources of packets (corresponding to underlying queues) 2) Unioning of classes – essentially, merging a series of classes into one large superclass. 3) Set-To-Stream Policies – Policies which, given either a class or union of classes, operate over their underlying packets as a whole. 4) Stream-To-Stream Policies – Policies which take in a series of streams – sources of intelligent policy-specific packet flows, and operate over only the heads of each stream to determine which packet to process.

With that in mind, we can define set-type elements and stream-type elements in the language:

Inductive SetType := 
| Class (c : nat)
| Union (cq: list SetType).

Inductive StreamType :=
(* Set-to-stream *)
| FIFO (c : SetType)
| EDF (c : SetType)
| SJN (c : SetType)
(* Stream-to-stream *)
| RoundRobin (pq : list StreamType)
| Strict (pq : list StreamType).

Here, we define a series of policies. We have set-to-stream policies:

1) FIFO (First-In-First-Out) dictates that the first packet seen (pushed in with some rank), will be processed. 2) EDF (Earliest-Deadline First) dictates that the packet whose deadline comes first will be processed first. 3) SJN (Shortest-Journey Next) dictates that the 'lightest' packet is processed first.

And stream-to-stream policies:

1) Round-Robin policies arbitrate over multiple streams, popping one at a time from each stream, thereby creating a sense of balance. 2) Strict policies arbitrate over multiple streams. However, a policy will stay on one substream until it falls silent (stops having poppable packets) and then moves to the next one.

Thus, we can define semantics for operations w.r.t each of these specific policies, and run with that.

We then define a tuple of state – a Rio program, followed by a series of queues corresponding to its classes, containing the relevant packets.

(* Definition of state in the context of Rio semantics. *)
Definition state := (StreamType * list queue)%type.

And both push and pop operations, operated over state tuples, to access packets and update state:

(* Push packet to specific queue within a list of queues, if present. *)
Definition push (input : (packet * queue * state)) : state :=
match input with
| (pkt, q, (prog, qs)) =>
    if queue_mem q qs
        then (prog, update q (enqueue pkt q) qs)
        (* If not present, return queues as they are. *)
        else (prog, qs)
end.

(* Pop the next enqueued packet from a Rio state tuple. *)
Definition pop (st: state). Admitted. (* Omit for brevity *)

With that, we can prove certain things – for example, that unioning a single element has no effect on the resultant piped into a FIFO Transformer. This extends to any set-to-stream transformer, which we prove (though omitted for the blog post).

(* Proof for FIFO *)
Theorem SingleUnionFIFO : forall (qs : list queue) (n : nat),
equal_popped
    (pop (FIFO(Union([Class n])), qs))
    (pop (FIFO(Class n), qs))
/\ queues_equal_popped
    (pop (FIFO(Union([Class n])), qs))
    (pop (FIFO(Class n), qs)).

Or, for example, that unioning truly breaks any sense of ordering on its underlying classes. As we discussed earlier, a union in sets of classes is intended to merge all elements into one big class. When piped into a Set-To-Stream transformer (such as FIFO), the corresponding packets are handled without examining their initial classes or queues.

(*  Unordered equivalence of two queues.
    If sorted, they are element-wise equivalent,
    they have unordered equivalence.
*)
Definition unordered_equivalent {A : Type} (q1 : list A) (q2 : list A) (f : A -> nat) : bool :=
    list_equiv (sort q1 f) (sort q2 f) f.

Definition to_class (n : nat) := Class(n).

Theorem UnorderedFIFO : forall (qs : list queue) (c1: list nat) (c2: list nat),
    (unordered_equivalent c1 c2) id = true -> 
        equal_popped
            (pop (FIFO (Union(map to_class c1)), qs))
            (pop (FIFO(Union(map to_class c2)), qs))
        /\ queues_equal_popped
            (pop (FIFO (Union(map to_class c1)), qs))
            (pop (FIFO(Union(map to_class c2)), qs)).

(None of these proofs exceed more than a few lines; they follow wonderfully cleanly from the semantics). With that, we can formally verify several aspects of program equivalence, and program optimizations.

Future Work

Future work involves extending the semantics of this language to is larger AST (with more polices), and formally verifying more interesting aspects of the syntax. The ultimate goal (which was the initial premise of my project) is to show that as Rio programs are compiled to lower-down forms, the semantical meaning and decisions over which pacekts are popped, remain the same.

Concurrent KAT: decidable program properties for shared-memory concurrency

Mark Barbone

In this project, we introduce Concurrent KAT, a simple programming language with shared-memory concurrency, and verify a decision procedure for reachability.

Intro

Rice's theorem states that there is no decision procedure for any nontrivial program property of general programs, which is quite a bummer for program analysis, as ideally this is what we'd like to build. So we need to pull some kind of trick to get around Rice's theorem, and there are (more or less) three main ways it's usually done.

  1. Weaken decision procedure: You can (soundly) approximate the property of interest, for instance, answering Yes, No, or IDK, as in abstract interpretation.
  2. Weaken program property: A program property just depends on the behavior of the program, not how it's written. By specifying our property of interest as a syntactic property of the program, we can hope to decide it: the Hindley-Milner algorithm decides whether a program is well-typed, but being well-typed depends on how the program is written.
  3. Weaken general programs: Lastly, if we work with a simple, non-Turing complete programming language, such as Kleene Algebra with Tests (KAT), we can have some hope at a decision procedure for non-trivial program properties.

In this project, we take approach #3. We extend (Net)KAT with a parallel-fork operation e1 || e2, and shared variables $X, Y$ between threads.

Details

The setup

Here's what our programming language looks like:

(* There are both thread-local variables and shared global variable *)
Inductive var :=
  | Local (name : string)
  | Global (name : string).

(* (Net)KAT-like syntax, with a Par constructor for parallel composition *)
Inductive expr :=
  | Drop                      (* stops execution of the current thread *)
  | Skip                      (* does nothing *)
  | Test (v : var) (n : nat)  (* continues executing only if v == n *)
  | Mut  (v : var) (n : nat)  (* assignment v := n *)
  | Choice (e1 e2 : expr)     (* non-deterministic execution, arbitrarily running e1 or e2 *)
  | Seq (e1 e2 : expr)        (* sequential composition e1; e2 *)
  | Star (e : expr)           (* repetition (e)* -- runs e an arbitrary number of times *)
  | Par (e1 e2 : expr).       (* forking (e1 || e2) -- forks the thread into e1 and e2 *)

Besides Par, everything here is from NetKAT (though we don't quite have all of NetKAT).

We also have a small-step operational semantics, which says when one state steps to another. A state is a tuple (h, m), where:

(* Small step for a single thread *)
Inductive step1 : (Heap * Pk * expr) -> State -> Prop :=
| ....

(* Small step for whole states: pick any one thread and run it one step *)
Inductive step : State -> State -> Prop :=
| step_step1 h1 h2 pk e m' m :
    is_Some (m !! (pk, e)) ->
    step1 (h1, pk, e) (h2, m') ->
    step (h1, m) (h2, mcup m' (mremove (pk, e) m)).

We mainly work with rtc step, the reflexive-transitive closure of step.

The decision procedure, informally

Intuitively, because there are only finitely many variables and values in the program, there are finitely many possible states for each thread to be in. In NetKAT, this gives us an algorithm: we do a DFS for reachable states, stopping if we see one we already came across. For Concurrent KAT, the challenge is that forking in a loop could generate unboundedly many threads.

For example, suppose we're in a state with 3 threads all in the same local (pk,e), and later we get to the same state except with 5 threads in local state (pk,e). In this case, the program could keep going around that path, spawning arbitrarily many threads in state (pk,e). So we check for this, and replace the counter for (pk,e) with a special symbol Infinity when it happens.

As it turns out, this is enough to guarantee termination of the DFS algorithm. A similar technique is used in abstract interpration, where it is called widening. Jules came up with the idea to use it here.

The decision procedure, formally

There are two main tricky parts in formalizing this.

The first is termination. To prove termination, we needed a very general kind of well-founded induction, using a well-quasi-ordering. (Nate pointed out that there's a connection between our problem and Petri nets, which are also used to model concurrency---and reachability for Petri nets is known to not even be in PR! So it makes sense we need a complicated termination proof.)

Our proofs about well-quasi-orderings are very classical, and make frequent use of LEM and the axiom of choice. This is OK because it's all in Prop: we can still extract working OCaml code for the decision procedure.

The second is correctness. Once we add multisets with Infinity, we're no longer computing the exact operational semantics (which, of course, does not allow for actually infinitely many threads): we're computing some abstraction of it. So we have a definition abstract_steps: in words, s1 abstractly steps to s2 if, for any instantiation of s2 with actual finite counts, there's a way to instantiate s1 that steps to something with at least those threads.

(* `inst n s` replaces all the Inf's in `s` with `n` *)
Definition inst (n : nat) (s : State) : State := ...

(* s1, s2 are abstract configurations (might have Inf). *)
(* this is the appropriate abstraction of the `rtc step` relation *)
Definition abstract_steps s1 s2 :=
  ∀ n, ∃ k s2', rtc step (inst k s1) s2' ∧ state_leq (inst n s2) s2'.

We proved the invariant that the algorithm only enumerates states abstractly reachable from the starting state (that is, abstract_steps start X).

The grand finale

In the end, we have a reachability function

Definition reaches (e : expr) (start_pk : Pk) (end_pk : Pk) : bool.

and a theorem

Theorem reaches_correct e start_pk end_pk :
  reaches e start_pk end_pk <->
    ∃ state, rtc step (∅, msingle (start_pk, e)) state ∧ is_Some (state.2 !! (end_pk, Skip)).
Proof.
  ...
Qed.

Demo

You can extract and run it! Here's a brief example (using some Coq Notation syntactic sugar).

Definition example_program : expr :=
  X <- 0;
  (Test X 0; Test X 1; f <- 1) || (X <- 1).

Definition f_is_zero : Pk := {[ "f" := 0 ]}.
Definition f_is_one  : Pk := {[ "f" := 1 ]}.

This program sets the flag f to 1 in the left thread when it sees X == 0 then sees X == 1. Extracting it to OCaml, we can ask:

utop # reaches example_program f_is_zero f_is_one ;;
- : bool = True

Proving compiler correctness for a sequential hardware description language that describes parallel behaviors

Yulun Yao

Proving compiler correctness for a sequential hardware description language that describes parallel behaviors

Background

PDL is a novel hardware description language (HDL) that uses a sequential programming model to describe pipelined processors, which exhibit parallel behaviors and are hard to reason about. PDL’s definition of correctness is called One-Instruction-At-A-Time (OIAT) semantics. Formally, it is a weak bi-simulation relation over observations (i.e. trace of memory writes) in between sequential specification and parallel implementation. Formalizing PDL is a complex task given the complexity of the language and hardware’s parallel behavior.ERR: Diagram not loaded!

Sequential and parallel semantics

PDL’s sequential semantics represent its sequential specification. It looks exactly like a single-threaded, sequential, imperative program, and works just like that: all the colored command does not have any real effect, that is, only the functional logic that describes how to process a single thread (one pipeline call) works. The Call statement is the only exception here: when the call statement gets executed, the entire pipeline will be called with the passed argument, like a function call. However, this function call is deferred till the current execution of the functional logics are finished. Another way to think about this is that call statement modifies the continuation after the current pipeline call.

PDL’s parallel semantics closely resembles real hardware. In hardware, circuits are executed every cycle, if activated. Each pipeline stage (separated by three dashes) can be viewed as a circuit running independently. At this level, we lost the high level understanding of the pipeline, and even finishing up one pipeline call requires collaboration of circuits doing their own work. This shows a paralleled behavior 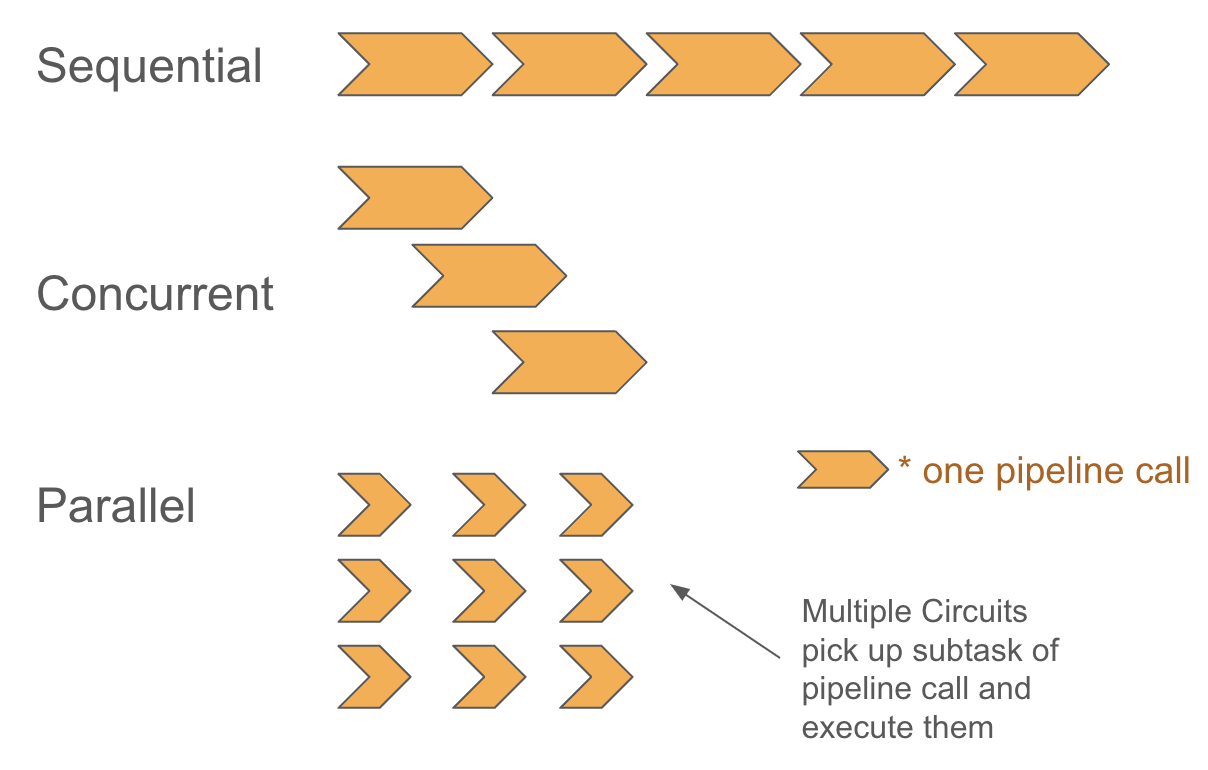ERR: Diagram not loaded!.

Bridging the gap

While there is a big gap in between sequential and parallel semantics, if we look at our pipeline abstractly, we would notice that multiple pipeline calls can make progress at the same time. This is similar to having multiple threads running concurrently (see diagrams). The concurrent behavior is constrained by the sequential specification, and the parallel implementation will closely resemble this concurrent behavior. Therefore, if we can capture the semantics of this concurrent behavior accurately, we could have a foothold to bridge the gap and thereby finishing our proof. Thus the big bi-simulation relation can now be divided into proving bi-similarity in between sequential semantics and concurrent semantics, and bi-similarity in between concurrent semantics and parallel semantics.

Vision

For this project, my initial goal was to formalize the equivalence relation (bisimulation) between my sequential and parallel semantics. However, I realized that I don't yet have a clear paper-and-pen proof on bisimulation, and Coq is not lenient in dealing with unimprovised theorms and proofs! Therefore, I scaled back the project significantly and decided to first prove the well-formedness properties of my language, which I think would be some of the key stepstones.

Achivement

For this project, I built an interpreter for the core subset of PDL and tried to prove some wellformedness conditions, as well as properties of my core language features. Specifically, how lock preserves program order, and how lock placement affect the OIAT. Aside from these, I proved some properties about Bits, which could be useful eventuallyERR: Diagram not loaded!.