CS 4621 PPA1 WebGL Ray

Out: Friday September 7, 2018

Due: Friday September 21, 2018 at 11:59pm

Work in groups of up to 4. You can group up on Piazza.

Overview

In this programming assignment, you will implement a simplified GPU version of the CS4620 raytracer (Ray 1). The goal here is not to reproduce all the features we have seen in the other assignment, but rather to give you some practice programming WebGL applications.

WARNING: WE THINK THIS ASSIGNMENT IS LONG. START EARLY.

Requirements

Note that this video was recorded by Pramook Khungurn for the Spring 2017 version of this class. The assignment has changed in places, but everything in this video is up to date.

Logistics

First, download the starter code. We recommend creating a git repository for development, but please don't share your code publicly.

Inside the directory, open index.html, and you should see something like this.

template web page for ppa1

Please modify index.html so that it performs ray tracing and shows the output in the black canvas on the top of the web page. You may also add other code to the directory. However, do not use any 3D rendering frameworks such as three.js. Linear algebra libraries such as glMatrix are fine. Our solution code, however, does not use any extra code besides what is already in the ZIP file.

Once you're done writing your solution, ZIP the directory, and submit it to CMS.

Implementation Details

Camera and Ray Generation

Instead of the more involved camera model in the Ray 1 assignment, the camera model in this assignment is a little simpler. It is specified by 4 parameters:

To generate rays from the camera, first form an orthonormal basis $[\mathbf{x}, \mathbf{y}, \mathbf{z}]$ as follows: \begin{align*} \mathbf{z} &= \mathrm{normalize}(eye - target) \\ \mathbf{x} &= \mathrm{normalize}(up \times \mathbf{z}) \\ \mathbf{y} &= \mathrm{normalize}(\mathbf{z} \times \mathbf{x}) \end{align*}

The image plane is parameterized by $(x,y)$ coordinates where both $x$ and $y$ ranges from $[-1,1]$. So, consider drawing a full screen quad so that the bottom-left corner corresponds to $(-1,-1)$ and the top-right corner corresponds to $(1,1)$.

All rays originate from the camera's eye position. The ray associated with image plane coordinate $(x,y)$ has direction: $$\mathbf{d} = \mathrm{normalize}(-\mathbf{z} + (s\ x)\ \mathbf{x} + (s\ y)\ \mathbf{y})$$ where $$ s = \tan \bigg( \frac{\pi}{180} \frac{FOV}{2} \bigg).$$ In other words, we convert $FOV/2$ to radian and compute its tangent. Note that the ray starts right off from the eye position, not from a plane that is in front of it. This is because our camera model does not have something equivalent to projDistance in the Ray 1 assignment.

The camera can be controlled by the GUI elements in index.html. Its JavaScript code contains the convenience methods for retrieving the camera parameters:

Call these functions every frame, and pass their return values to your shader.

Light Source

Every scene in this assignment has one point light source, and it is defined by two parameters: its position and intensity. These parameters can be controlled by GUI elements, and the template code provides the following functions for retrieving their values:

Again, call these functions every frame, and pass their return values to your shader.

Background Color

If the eye ray does not hit any geometry, your shader should set the pixel to the background color that is specified by the GUI in index.html. Use the function getBackgroundColor() to retrieve its value.

Scenes

In the template code, we have included three scenes that you can render: the "triangle," the "cube," and the "full" scene. You can switch between theme through the GUI. In JavaScript, use the getScene() function to retrieve the current scene specified by the GUI.

The value returned by the getScene() function is a JavaScript object with the following fields:

This is similar to indexed structures you've seen before, except colors are specified for each face rather than for each vertex. Note that none of the meshes have normal or texture coordinate data. If you would like to know how the scene objects are created, read scenes.js.

In your shader, you should create a uniform array that stores all of the indices for the triangles. For example: 

uniform ivec4 triangleIndices[MAX_TRIANGLES];
The full scene is the largest scene, and it contains 132 triangles, so you can set MAX_TRIANGLES to $132$.

To transfer the vertex positions and triangle colors, you'll need to use textures, as uniform arrays can only be accessed monotonically (i.e., with loop variables and constants). Within your fragment shader, you can use samplers to access these textures: 

uniform sampler2D vertexPositions;
uniform sampler2D triangleColors;

Note that transferring lots of data to the GPU is a slow operation. These scenes are small enough that you shouldn't encounter performance problems if you update triangleIndices, vertexPositions, and triangleColors on every frame (and you will not be penalized if you do this), but we recommend only updating these variables when necessary (i.e., when the user changes which scene is displayed), since this is good practice.

Render Modes

Your ray tracer should support the following rendering modes

The render mode can be changed by the GUI. You can retrieve the current rendering mode in JavaScript by calling the getRenderMode() function. It returns an integer where $1$ means the face color mode, $2$ means the normal mode, $3$ means the shadow mode, and $4$ means the full mode. Pass this value to your shader every frame.

WebGL Limitations

The WebGL specification was written for hardware with limited capabilities, so there are some operations you would be able to do in normal programming languages but cannot do in GLSL.

  1. If you write a for loop, the number of iterations must be known at compile time. This means that you cannot do something like this: 
    uniform int numTriangles;

for(int i=0; i<numTriangles; i++) {
    :
    :
}
    But you can do something like this: 
    const int MAX_TRIANGLES = 132;
uniform int numTriangles;

for(int i=0; i<MAX_TRIANGLES; i++) {
    if (i >= numTriangles)
        break;
    :
    :
}
  2. Array access in the fragment shader is limited. You can only index an array with an expression made up of loop counters and constants. In other words, if we were to store vertex positions in a uniform array, the following would be okay: 
    uniform vec3 vertexPositions[MAX_VERTICES];

vec3 p = vertexPosition[0];

for(int i=0; i<MAX_TRIANGLES; i++) {
    vec3 a = vertexPositions[3*i];
    vec3 b = vertexPositions[3*i+1];
    vec3 c = vertexPositions[3*i+2];
    :
    :
}
    But, this is not: 
    uniform vec3 vertexPositions[MAX_VERTICES];
uniform int vertexIndex;

vec3 p = vertexPositions[vertexIndex];
    This is why we are storing the vertex positions and triangle colors in textures; any piece of a texture can be accessed by any pixel. This way, you can loop over all triangles by looping over the triangleIndices array.

WebGL Features

When writing a function, you can use the keywords to quantify function parameters so that you can pass values back from the function as well. This is very useful when writing a function that has more than one return value. The relevant keywords are out and/or inout. Using them, you can do this: 

void computeSomething(float x, out float y, inout float z) {
    y = x + 1.0;
    z = 2.0*(x+z);
}

void main() {
    float a;
    float b = 2.0;
    computeSomething(5, a, b);
      :
      :
      :
}
After computeSomething is called, a becomes 6, and b becomes 14.

Programming Tips

This may all seem a little daunting. This project contains many pieces in a language (or, potentially, in languages) that you have never used before. Additionally, debugging is difficult; JavaScript has the advantage of console.log(...), but there is no way to print out values in GLSL code.

We strongly recommend taking the following advice:

KEEP CALM AND INCREMENTALLY ADD FEATURES.
Do not implement all features at once without testing them individually. You will end up with a black canvas, and you will have no idea what parts of your code aren't working. Break the assignment to easy-to-finish and easy-to-test pieces. Here is a possible road map.

  1. Initialize WebGL.
  2. Write a shader that draws the full screen quad and make sure it works.
    • The easiest way to do this is to make use of the code in Exhibit #6 of Lecture 2.
    • What are the texture coordinates of the 4 corners of the full screen quad in Exhibit #6? Are they the most convenient for this assignment?
  3. Have your shader output the background color.
  4. Have your shader generate the rays. Before attempting to intersect them with the scene, output the ray direction as a color, using the same conversion from direction to color as with the normal render mode. You should see the canvas change as you change the FOV, camera location, or camera target.
  5. Work on the face color mode, i.e., ray intersection.
    • Learn how to create and use uniform arrays from Exhibit #3 of Lecture 2.
    • Learn how to create and use textures from Exhibit #0 of Lecture 3.
    • Write your code to intersect just the first triangle in the mesh first.
    • Get your code to work with the "triangle" scene, which has only one triangle.
    • Then, write a for loop that goes through all the triangles to find the first intersection.
    • Then, try to get the "cube" scene to work.
    • Once you're confident, run your code on the "full" scene.
    • From our experience, this step is the hardest because ray tracing is complicated in itself. It's also very easy to trip up over little details. Be patient here.
  6. Work on the normal mode.
  7. Work on the shadow mode, i.e., shadow ray casting.
  8. Work on the full mode.

We would also like to remind you that the exhibits are for you to use. However, do not just copy and paste them in your code. Read and understand them so that so you can modify them to do your bidding. Also, make use of the code you wrote for the Ray 1 assignment. If you have to get a part of Ray 1 fixed first, come to us for help.

To help you check your progress, below are screenshots of the reference program's renderings of the three scenes under all the modes below.

Triangle Scene Cube Scene Full Scene
Face Color Mode
Normal Mode
Shadow Mode
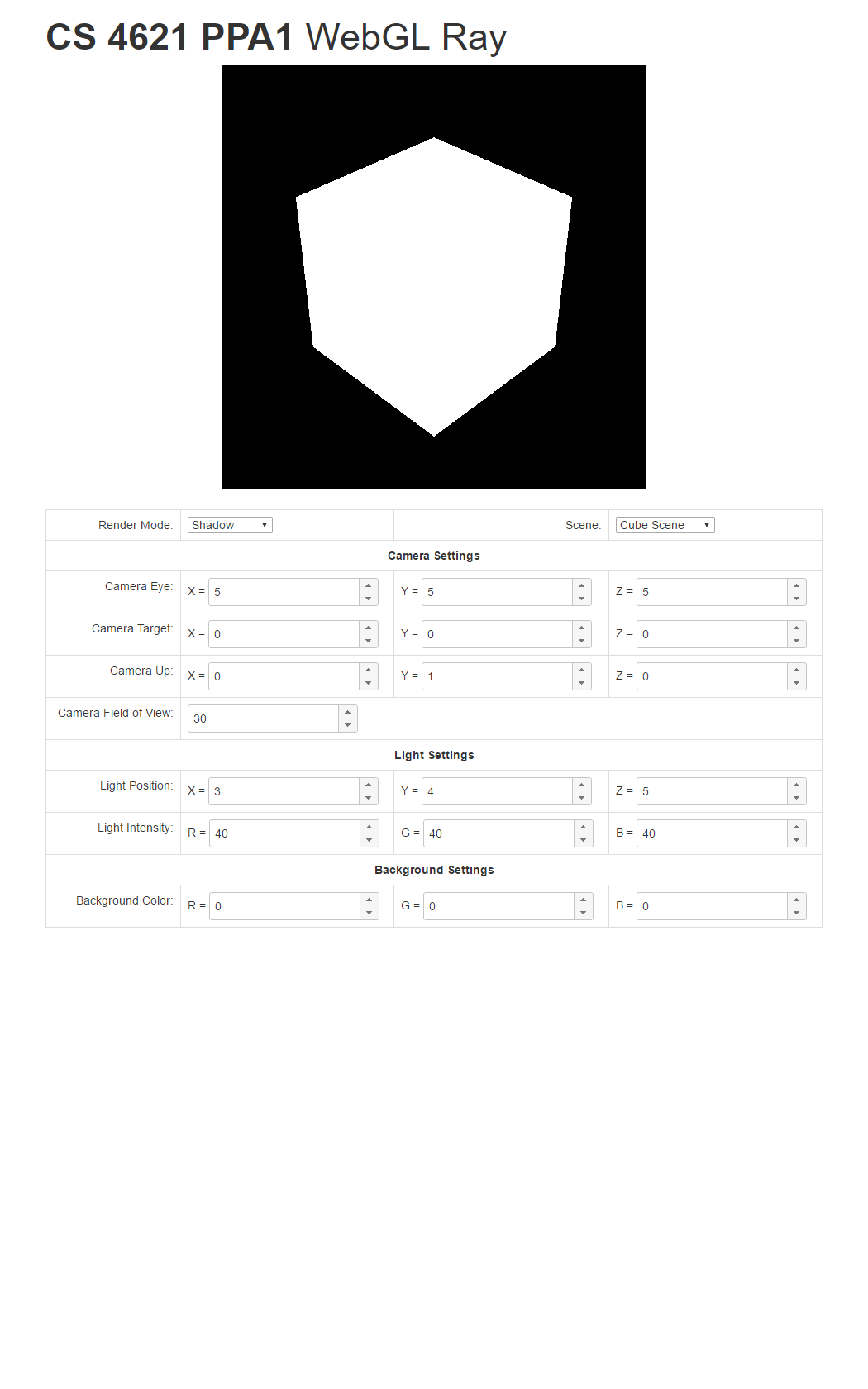Full Mode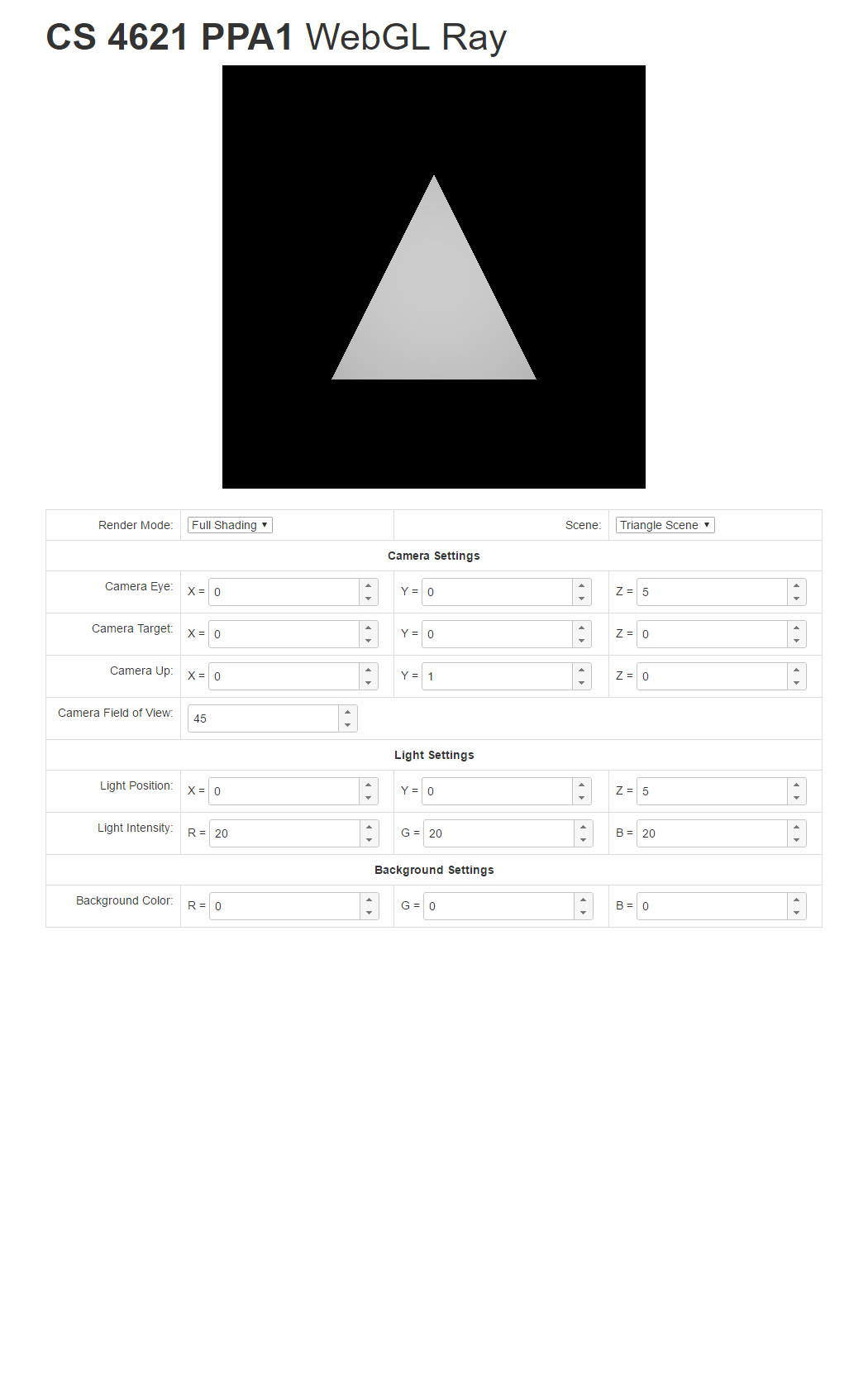

Remember, though, to make up new test cases on your own because we will do so to test your program too. Change the background color. Move the camera and the light around. What happens when the light is inside the bunny or the box? Does your program's behavior make sense?