Abstract
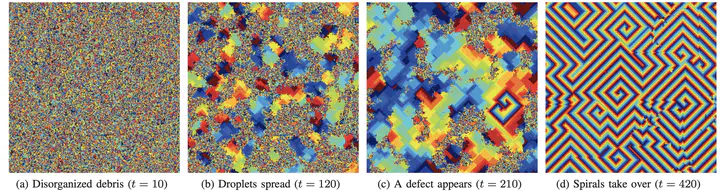
The cyclic cellular automaton (CCA) model of excitable media displays remarkable spiral wave behavior and evolves through distinct phases. Previous work has shown that the number of states $k$ plays a pivotal role in the long-term behavior of the system, but there has been no systematic investigation into its phase lengths. We provide an empirical method for determining phase start and end points and describe the dependence of CCA phase lengths on $k$. We find that the length of each phase exhibits a distinctive power-law relation with k in a manner independent of lattice size. In addition, we perform bootstrapping and parameter sensitivity analysis to determine the uncertainty in the power law exponents and coefficients.
Note: I was very disappointed by the quality of the conference. I do not plan to submit here again and I encourage other researchers to avoid it as well.
Kiran Tomlinson
PhD Candidate, Computer Science
I’m a Computer Science PhD candidate at Cornell University advised by Jon Kleinberg, researching social choice and preference learning.