Abstract
Typhoon is a backup/archival system that is designed to increase the availability of data by allowing file servers to distribute archival copies of files across an arbitrary set of servers. The system uses linear-time erasure codes as a means to recreate data in the event that one or more servers fail. The implementation that is described can tolerate failure rates that approach 50% while only using an aggregate amount of disk space that is comparable to a conventional file mirroring system. As a result, files will still be available in the event of server failures, provided that a sufficient amount of the data network is still functioning.
Keywords: Archive, Erasure Codes, Data Storage, and Availability.
1. Introduction
As computers become more prevalent in everyday life, our dependence and reliance on electronic data has progressively increased. This reliance on data, both in terms of explicit and implicit dependencies, is most noticeable when our access to important information or data is restricted due to a server failure. We have developed an archival data system called Typhoon that addresses this issue by allowing files to remain available to users by disbursing copies of files to other servers in a network.
Rather than distributing whole copies of files, Typhoon only places a portion of a file on each server. Before distributing data to other servers, each file is encoded using an erasure code that will allow Typhoon to automatically recover the file in the event that one or more servers (up to one-half) become inoperable. This degree of availability sharply contrasts most conventional data systems that become unavailable after a single server has failed.
In section 3 we provide an overview of erasure codes and describe the encoding and decoding algorithms for a particular type of erasure codes called “Tornado Codes.” Section 4 describes the overall architecture of the Typhoon archival system. A performance analysis of the system is provided in section 5, and section 6 discusses future work.
2. Related Work
Tornado Codes have been the focus of numerous papers, with [AL95], [LMS97], and [LMS99] being the most prevalent examples. Many other papers also provide supplementary theory for how the codes work, or how then can be improved. Such papers include [LMS98a], [LMSD98b], [LMSD98c], [SS96], and [SS99]. One of the most commonly cited applications for Tornado Codes is related to Reliable Multicast and Forward Error Correction (FEC). The original idea for this use of erasure codes is typically accredited to [RV97], which used an implementation of Reed Solomon codes utilizing Vandermonde Matrices. One example of a relatively efficient Reed Solomon Code utilizing Cauchy Matrixes is described in [BKL95].
[BLM98a] and [BLM98b] are among the first papers to propose an application for linear-time erasure codes, and they are also the first papers to refer to these codes as Tornado Codes. [BLM98a] describes a system for reliably distributing large files to multiple clients over an unreliable broadcast medium, such as multicast. The “Digital Fountain” continuously broadcasts an encoded file in a cyclic manner in order to allow clients to download portions of the files at arbitrary points in time. [BLM98b] describes a similar system that uses multiple servers and/or layered multicast in order to increase the transmission rate of data. Both of these systems are designed for one-way, read-only transmissions of data to client computers.
The “Intermemory” project is working to create a long-term, distributed data storage system. The philosophy of the project is described in [GY98]. Their prototype operates in a manner similar to Typhoon, except that the system uses Reed Solomon Codes, has a much higher overhead in terms of the total amount of disk space used for each file, and can not tolerate as many simultaneous server failures. The working prototype, as described in [CEGS98], is a read-only system.
[K99] provides an overview of “OceanStore”, which is a research project working to create a ubiquitous, highly-available, reliable, and persistent data storage system. Although the system is similar to Intermemory, it does provide some other key benefits, such as secure data (e.g., use of encryption, and untrusted networks/servers), read-write behavior, and data introspection (for moving data closer to clients in order to increase performance). Typhoon was specifically developed with OceanStore in mind, although it is still suitable for other applications.
3. Erasure Codes
Erasure Codes comprise a key aspect to the
Typhoon System, since they are what makes it possible for Typhoon to cope with
multiple server failures. The idea of
an erasure code is to partition data into blocks and augment the blocks with
redundant information so that error recovery is possible if some part of the
information is lost. In the case of
Typhoon, these blocks are randomly distributed to other servers.
The “Reed Solomon” family of erasure codes are quite popular, but their quadratic computation time makes them practical to use on only the smallest of files. Some types of Reed Solomon Codes (e.g., Cauchy-based Reed Solomon) have slightly smaller computational requirements, but these types of codes are still unreasonably slow. To help make the Typhoon System a realistic solution, we created and developed an erasure code algorithm that belongs to the linear-time erasure code family called “Tornado Codes.”
A Tornado Code is much more
efficient than a Reed Solomon Code, but this is largely because Tornado Codes
were invented through the use of probabilistic assumptions and proofs. As a result, Tornado Codes typically require
a larger amount of data, compared to a Reed Solomon Code, before an arbitrary
file can be restored. For example, a ½
rate Reed Solomon Code can decode a file using exactly half of an encoded file,
while a Tornado Codes would require slightly more than half of the data (5 to
10% is typical, although the value can vary).
The net result is a tradeoff between a slight increase in network
traffic for a drastic drop in computational requirements.
3.1 Encoding Algorithm
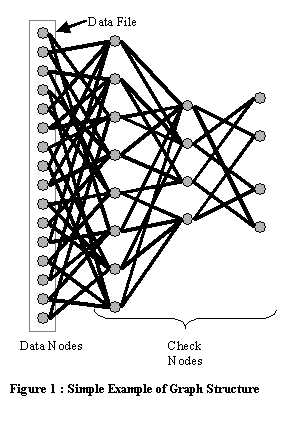
The encoding process that is used by a Tornado Code is simple to describe, yet it can be difficult to implement in a correct manner. After partitioning a file into a set of equal size fragments called “data nodes”, the algorithm creates a set of “check nodes” that are equal in size and population to the data nodes. Using a series of specially designed bipartite graphs (as depicted in Figure 1), each check node is assigned two or more nodes to be its neighbors, and the contents of the check node is set to be the bit-wise XOR of the value of its neighbors. Because each of the nodes are sequentially numbered, the encoded file can then be distributed in pieces containing one or more nodes.
The aspect that makes Tornado Codes interesting is the graph that is used by the encoding and decoding process. The derivation process can be quite complex for creating graphs with an efficient structure (where efficiency is defined in terms of the average number of nodes that are required to reconstruct a file). The research papers that provide the specifications for Tornado Codes involve a great deal of mathematical theory. Some of the papers also contain errors that can exacerbate the difficulty in implementing a Tornado Code. We have included an appendix to this paper that provides a detailed explanation for implementing a particular type of Tornado Code. In the spirit of [PL99], the explanation is targeted for persons who do not have a solid foundation in statistics or mathematical theory.
3.2 Decoding Algorithm
The decoding process is symmetric to the encoding process, except that the check nodes are now used to restore their neighbors. A check node can only recover data if the contents of that node is known, and only one left-neighbor of that node is missing. To restore the missing node, the contents of the check node is XORed with the contents of its left-neighbors, and the resulting value is assigned to the missing neighbor.
Because the Tornado Code graph is created to satisfy a certain set of constraints, if the nodes were received with a random distribution, then there is a high probability that the decode process will succeed. This success is “guaranteed” by the fact that during the decode process there will always be at least one check node that is missing only one neighbor. If the nodes were received using some other type of distribution, then the decoding process will still succeed, provided that a sufficient number of nodes are received. As a result, the inventors of Tornado Codes suggest that nodes be transferred over a network in random order in order to minimize the effect of certain types of network data loss behavior (e.g., bursts).
4. Architecture
We have implemented three variants of Typhoon. The first two are identical except that one uses a Cauchy Reed Solomon Code, while the other uses the Tornado Code that we developed for this project. These two systems were developed to model the overall structure of “OceanStore”, a global ubiquitous data storage project at UC Berkeley that utilizes cryptography to ensure the privacy of data. This model is comprised of a client machine that generates read/write requests, a caching server for increasing the speed at which client requests are serviced, and one or more sets of servers (called “pools”). Each server is running a “replication mechanism” and a “filestore.”
The replication mechanism encodes (decodes) a file and communicates with the filestores to distribute (gather) pieces of a file. A filestore’s only task is to store, or transmit, fragments of a file. In addition, a “Naming and Location Service” (NLS) is also provided to track which pool should be used to store or retrieve a particular file. For file updates we used a versioning scheme where the NLS assigns a unique internal name to each version of a file.
These two systems were developed using straight-forward techniques and could therefore benefit greatly from a series of optimizations. The third implementation we created is a multithreaded system that contains a reasonable level of optimizations, but its scope is limited to the activities that occur within a server set (i.e., there is no caching mechanism, file requests originate at the server, and the role of the NLS has been externalized).
4.1 OceanStore-based Implementations
To retrieve or store file fragments, a request is sent to the members of a particular set of servers, called a “pool”. These requests are made on an individual per-server basis, and the member-list for each pool is provided by the NLS. The NLS service is a simple single-server daemon that was used in place of a full-scale OceanStore implementation that has yet to be developed.
After a request has been received by a server, it must choose whether to respond to the request. Because a server can choose to ignore a request, each member of the pool has the freedom to perform load balancing by accepting new requests only when the load of the server is not excessive. If the majority of the pool members are busy, then other mechanisms (such as rebroadcasts of requests, or a priority mechanism) would be necessary in order to prevent certain forms of starvation.
In the case where a server is archiving a file, the contents of the file is randomly distributed to willing servers after the encoding process has completed. The retrieval process is similar, except that multiple simultaneous data streams are being sent to requesting server. Although the decoding process does add some latency to a file request, some of this latency is offset by the large aggregate rate at which the server receives file fragments from multiple servers simultaneously.
At stated above, the OceanStore implementation was created to provide a means for experimenting with the complete end-to-end model of the OceanStore project. In evaluating this system for performance, we disabled caching in order to amplify the system load during performance evaluation. As expected, the naming system and the single-threaded nature of the implementation both served to increase latency and degrade overall performance.
4.2 Server Set Implementation
This implementation was designed to be an efficient, bare-bones system that would allow us to gauge the upper limits on performance, and to study how a Typhoon system would handle network related issues such as latency and packet loss. The simplicity of the system made it feasible for us to experiment with various mechanisms for improving performance, such as multithreading and MMX.
Instead of an explicit naming service, this implementation has the ability to use either server lists or multicast to identify the members of a pool. A server list is a static-assignment approach that would be useful for situations where changes in server topologies are infrequent, or in cases where a central directory mechanism is not available. A similar approach would involve using a DNS-like naming hierarchy as a way to assign servers to particular groups.
In the case of multicast, a server would implicitly join one or more pools by listening to particular multicast sessions. This approach for pool management is ideal for server configurations that change on a frequent basis. Because of issues with the UC Berkeley network, we were unable to fully evaluate the benefits of using multicast.
Although multicast makes it possible to selectively broadcast a request to multiple servers using a single IP packet, we did not find significant savings in terms of latency (which is not surprising, considering that the broadcast could not transmit beyond a single subnet). One aspect we have yet to study is whether multicast might prove beneficial on a large scale basis, since the server list approach involves sending a “rapid-fire” series of request packets that could potentially be dropped by a network router.
4.2.1 MMX Enhancement
The “Server Set” implementation was designed to be compatible with both UNIX and Windows without requiring any code to be ported. Although most of our experiments were run on Sun Ultra 5s using Solaris 5.7, we did occasionally use Microsoft Windows™ to experiment with various aspects of the system. One of the more notable experiments involved enhancing the XOR portion of our Tornado Code algorithm by writing assembly code that utilizes the MMX features of the Intel Pentium II Processor.
The MMX instruction set allows for 64-bits to be loaded from memory, XORed with another 64-bit register, and stored back to memory using only three assembly instructions. Compared to the naïve approach of XORing data arrays in increments of 8-bit chars, MMX runs faster by a factor of 1.9. After optimizing the assembly instructions for the processor’s dual-pipelines, the performance factor increased to 2.3.
However, after adding a few lines in our C++ code that cast the data to arrays of 32-bit integers, we found that MMX only provided a 50% improvement over XORing 32-bits at a time. Due to Amdahl’s law, the overall improvement to the execution time of the encoding algorithm is only 2.07%.
4.2.2 Multithreading
As expected, multithreading does provide a significant performance boost (as shown in the next section). To our knowledge, this system is the first to use threads to overlap the CPU-bound nature of Tornado Codes with the I/O-bound nature of network communication. Some of the performance gains we observed were noticeably better than what we expected.
All prior systems using Tornado Codes alternate an encoding phase with a data transfer phase. These systems not only underutilize resources, but they can also cause an excessive amount of data to be transferred over a network since a decoding phase must occur before it can be determined if a sufficient amount of data has been received for reconstructing a file. With our implementation, a server can simultaneously receive and decode data, and is thus able to immediately cease the retrieval process once the entire file has been recovered.
5. Performance
In this section, we discuss and analyze the performance of implementations of the Typhoon System. Our primary goals were to obtain an estimate on the upper limit of the speed of the system, compare the results of the Tornado Code system against the Reed Solomon system, and to examine how the system performed when driven by a 24-hour trace of NFS requests.
5.1 Estimated Bounds on Performance
One of the first experiments we performed was to evaluate the throughput of the algorithms on our test machines (Sun Ultra 5s). We found that the speed at which data is encoded using our Tornado Code was dependent more on the size of the individual nodes in the graph than the size of the files. For example, if each node stores 1Kb, then the algorithm averages 4.91 MB/sec.
As the node sizes decreases, the throughput also decreases because a larger number of nodes are now needed to encode or decode a file. This increase in node count also increases the size of the graphs, which leads to a higher amount of overhead. As a result, using 512B nodes results in an average throughput of 3.80 MB/sec, and 256B nodes average 2.62 MB/sec.
In heavy-use situations we expect the
average throughput to decrease due to the additional overhead from context
switches, VM activity (e.g. increased page swaps) , and contention for the
network. One of the foundational
assumptions of the OceanStore project is that fast networks will be available,
so we did not model the network as the bottleneck. Because our load-balancing technique (as described above) calls
for heavily-loaded servers to not respond to requests, we did not model network
peers as a potential bottleneck.
We should also mention that it is not possible to use large nodes for small files. This is because the decoding process performs better with a larger number of nodes. Our Tornado Code implementation is largely based on [LMS99], which reports that the amount of data overhead (i.e., the quantity of data which exceeds the amount needed by a Reed Solomon Code) is approximately equal to the original file size times 1/(node count0.25).
This overhead estimate suggests that a graph must have at least 10,000 nodes before the overhead is less than 10%, and our observations concur with this estimate. In light of these findings, a Reed Solomon code would be a better choice for particularly small files. In addition, files of inconsequential size, such as four bytes, would have to be inflated in size (e.g., through replication or automatic “tarring” with other small files) so that there is a sufficient amount of data to spread over multiple servers.
5.2 Reed Solomon vs. Tornado Code
As expected the performance of the Tornado Code system is far superior to the Reed-Solomon system. The Reed-Solomon based Typhoon system requires an average of 1877 seconds to gather and decode a 3 MB file, and it takes an average of 1306 seconds to encode and distribute a 3 MB file. In contrast, the multithreaded, Tornado-based Typhoon system takes only 1.5 seconds to retrieve a 3 MB file, and 1.313 seconds to store the file.
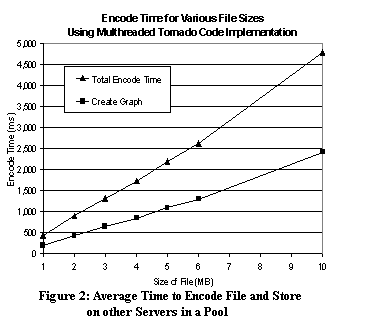
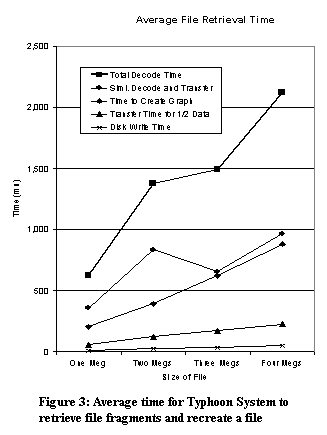
Figures 2 and 3 show the average time for the multithreaded Typhoon system to store and retrieve files of various sizes. Figure 2 shows that almost exactly half of the time is spent to create, at run-time, the graph that is to be used to encode the file. We found this result surprising, and will consider other options for future versions of the system.
5.3 NFS File Traces
To analyze our Tornado System’s ability to handle a “real” workload, we created an experiment to drive our OceanStore implementation using a trace of NFS disk requests. The trace was obtained by extracting the NFS calls present in the Instructional Workload (INS) trace collection from Roselli & Anderson [RA].
Because Typhoon only supports the reading and writing of files, the INS traces were first filtered to contain only open system calls, and then processed to change open system calls to retrieve or store requests to the Typhoon system. The type of request was derived using the open mode of the NFS request.
The INS trace contained file request information for nineteen servers, so we used an equal number of servers in the Typhoon System. We found that the Typhoon System can handle the workload of the traces, even when those traces are executed at three times the normal rate.
5.4 Network Latency
As part of our analysis we also studied how the Tornado based Typhoon system tolerates latency when servers are geographically apart. We constructed a tool that allows us to create arbitrary server topologies interactively using a graphical interface. An example screenshot from the program is shown in Figure 4. After a server topology is created, each of the constituents of our Typhoon implementation are automatically updated to artificially simulate a particular amount of latency. When a request arrives, the server purposely relays a response by an amount that is proportional to the physical distance between the two devices.
One of our first observations is that the impact of large network latencies between particular peers can be reduced by sending requests to a larger number of computers. For example, if a request is sent to only 60% of the devices that are storing fragments for a particular file, then it will be necessary to wait for all of those devices to respond.
However, by sending requests to a larger
“audience” (e.g., 80% of servers), then you have the option of only using the
subset of those servers that are the quickest to respond. Because of scalability concerns, it is not
advisable to “overestimate” the number of requests by a large amount (e.g., 90
or 100%). An intermediate solution (one that we used) involves a second phase
that tries to obtain alternates for slow servers. This second phase was used when too few servers respond to a
request within a specified time period (which was generally the time to compute
the Tornado Code graph, plus five seconds).
5.5 Server Failure
Our implementations of the Typhoon System were able to successfully cope with the loss of servers. In general, we found that a failure rate that exceeds 40 or 45% has the potential to prevent a file from being recreated. This percentage is not 50% for two reasons. The first reason is that Tornado Codes require slightly more than half the file, and the second reason is that we did not fully randomize the way in which file fragments were stored on servers.
Instead of sending each file fragment to a random recipient, a sequential sequence of file fragments were placed in a network packet. The quantity of file fragments per packet is dependent on how many could fit in a packet of a specified length. Although each packet is sent randomly to a particular host, this transmission method means that the loss of a server will cause small sequences of the encoded file to be lost.
This implementation approach essentially trades a reduction in transmission time for an increase in the time to retrieve a file. Given that Typhoon is an archive system, we expect that the quantity of writes will exceed the number of reads, and that there is some importance placed on how quickly a file is distributed to other servers.
In situations where file reads are more numerous such that retrieval times have extreme importance, or where network bandwidth is a premium, the use of a fully random distribution scheme is likely to be more beneficial. One way to implement this approach is to use “output buffers” that work in a manner similar to the GRACE hash-join algorithm, whereby an output buffer is allocated for each recipient and each node is randomly placed in an output buffer. Once a buffer is filled, the contents are sent to the corresponding recipient.
6. Future Work
There are a number of aspects to the Typhoon System that still need to be explored. One change that could increase performance would involve replacing the run-time graph creation approach with an implementation that loads pre-built graphs from disk. It would not be feasible to store every size graph on disk, but a more reasonable approach would involve composing large graphs using a set of smaller pre-built graphs that are stored on disk.
We did experiment with taking certain shortcuts in the hopes of reducing the time to create a graph. Although some techniques did have a marginal improvement, we found that all of our optimizations providing a large improvement in performance ended up creating inferior graphs that severely hindered the system’s ability to successfully recreate a file.
Data security is also an issue. One of the first discussions on security and its relation to deliberate server and/or network loss is [R89]. The paper proposes distributing data as a means to achieve security and reliability of data. Although this paper presents more questions than answers, it does present some useful considerations (and a few mathematical equations) that would be useful to keep in mind for an full fledged implementation of the system.
Some of the obvious ways to attack the current system involve sending corrupt file fragments to a server that is in the process of retrieving a file. Such an attack could cause incorrect files to be constructed. Even if a server can detect that the resulting file is corrupt, an implementation that performs a “retry” could leave itself open to “denial of service” attacks because a malicious person could also cause those retries to fail.
One possible solution is to use a form of signatures for each file fragment, but this could potentially add a significant amount of overhead (both in terms of data storage and encoding/decoding time). Many of these security concerns, and other issues for Typhoon, will be addressed by the OceanStore project.
Another item on our list is to address some of the concerns regarding disk behavior in a Typhoon System. This issue needs to be addressed based on the average number of fragments (per file) that are stored on each server. For example, if the ratio of file fragments to servers is significant (e.g., because fewer than 100 servers belong to a pool), then a file system suited for sequential writes, such as LFS [SBM93], may prove beneficial. Situations that involve hundreds of servers would require a more original approach, especially in light of the ever-increasing disk block size of most file systems.
Coordination of network traffic could also be explored. For large file transfers we found that the network bandwidth was completely monopolized during the data transfer period of a file. Although this behavior is expected (and desired) for rapidly transferring a single file, it’s likely to encounter scalability problems for a large number of simultaneous connections on a shared Ethernet (especially for implementations using UDP).
Disbursing servers over a wider geographic area does increase the amount of variation in latency between various servers, and this might help to reduce the magnitude of surges. We did find that packet survival rates improved by a noticeable margin on fully-switched networks, so this (and OceanStore’s assumption of fast, high-bandwidth networks) will help to alleviate this concern.
7. Conclusions
Using our three implementations of the Typhoon System, we have demonstrated that it is possible to maintain the accessibility of files in the event of server failures. The use of Tornado Codes provides a significant performance advantage over a system based on Reed Solomon Codes. In addition, the system can sustain a workload that was simulated using a series of file traces.
Although the file retrieval times are not outstanding, they are quite respectable, especially when compared to tape-based backup systems (or the prospect of no file access at all). In addition, we have identified several avenues that can be explored for increasing the performance of the system.
The overall Typhoon system is a realistic and viable solution that can be useful in many real-world situations. We also feel that the system’s level of availability and performance would also make it possible for the original copies of old or rarely used files to be deleted from the home machine. This would help to free disk space on machines, and the files could still be retrieved in the future by relying on the file fragments that are stored on other servers.