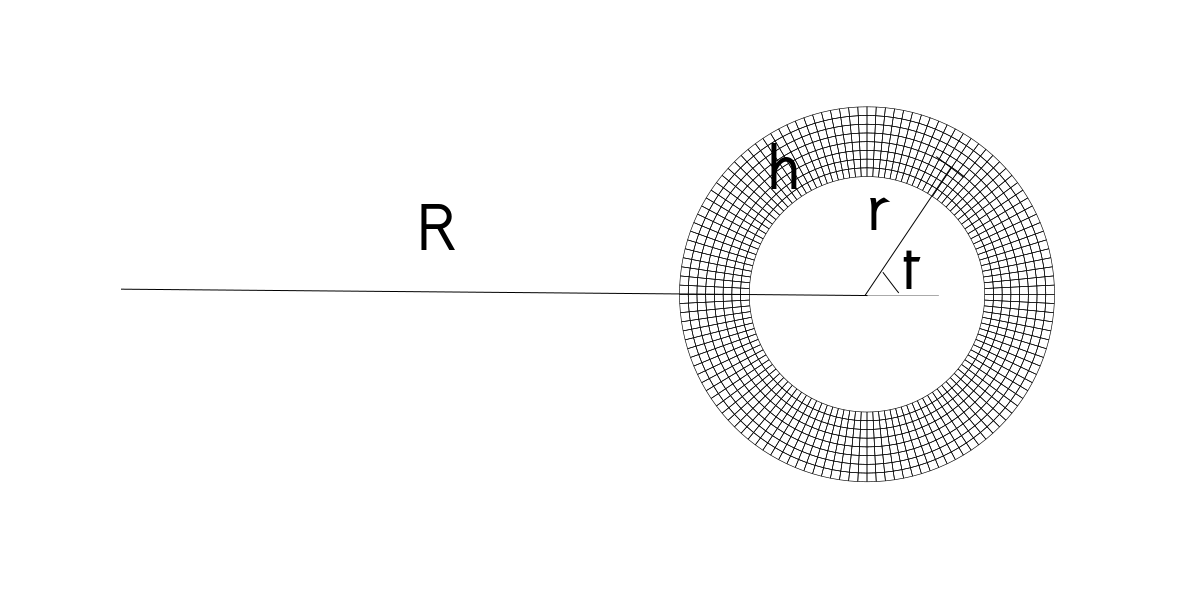
In this tutorial we will introduce merge block generator to construct more complicated geometries using multiple mapped blocks. We will investigate a toroidal shell resonator.
We will also show how to work with multiple files.
require "mapped_block"
require "merge_blocks" -- we will need `merge_blocks` functionWe can include materials defined in the file mymaterials.lua. We have defined get_materialname functions which take the unique material id and temperature as inputs, and returns the table required for add_material function.
require "mymaterials"
SILICON=get_silicon(0,300) -- material id:0, temperature: 300K
NITRIDE=get_nitride(1,300) -- material id:1, temperature: 300KWe are going to describe a toroidal shell, the upper half is made of silicon, and the lower half is made of nitride.

We will define two mapping functions, one for each half. They will map the reference domain \((x,y) \in [-1,1]\times[-1,1]\) to half annular regions. We will have intermediate values for the radial and angular position with respect to the circular axis. And then we will convert these values to the radial and axial coordinates with respect to the axis of revolution.
function torus_mesh_generator(R, r, h)
local function map_upper(x,y)
local rr = r + y*h/2
local t = (1+x)*pi/2
return R + rr*cos(t), rr*sin(t)
endThe lower half differs only in the sign of angular variable.
local function map_lower(x,y)
local rr = r + y*h/2
local t = -(1+x)*pi/2
return R + rr*cos(t), rr*sin(t)
end
merge_blocks function takes a list of blocks returned by mapped_block.
return merge_blocks { mapped_block {
phi = map_upper,
material = SILICON,
m = 64,
n = 8},
mapped_block {
phi = map_lower,
material = NITRIDE,
m = 64,
n = 8}
}
end -- of mesh generatorAs usual, we set geometric parameters and create a problem context.
R = 2.0e-3;
r = 3.5e-4;
h = 1.6e-4;
P = Problem:create{ params = {R,r,h},
m = 2,
meshgen = torus_mesh_generator }
We need to add both materials as tables returned by the functions defined in mymaterials.lua file.
P:add_material(SILICON)
P:add_material(NITRIDE)
P:mesh_gradient()
P:write_eps("torus.eps")
P:write_svg("torus.svg")
function free(r,z,d) return false end
P:set_boundary_conditions{ radial = {free},
angular = {free},
axial = {free},
temperature= {free}}
f0 = P:get_eigenfrequency() -- Eigenfrequency in Hz
BF = P:get_bryans_factor() -- Bryan's factor
Q = P:get_quality_factor() -- Q_TED
print("Frequency : "..f0)
print("Bryan's factor : "..BF)
print("Quality factor : "..Q )
df0dR = P:eigenfrequency_sensitivity(0)
dBFdr = P:bryansfactor_sensitivity(1)
dQdh = P:qualityfactor_sensitivity(2)
print("df0dR : "..df0dR)
print("dBFdr : "..dBFdr)
print("dQdh : "..dQdh )Finally let's write the displacement fields in inp format.
P:write_inp{"disp0.inp"; field=0}
P:write_inp{"disp1.inp"; field=1}
P:write_inp{"disp2.inp"; field=2}

