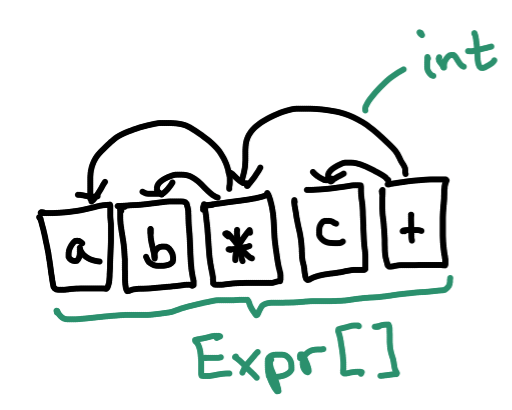
Adrian Sampson

Arenas, a.k.a. regions, are everywhere in modern language implementations. One form of arenas is both super simple and surprisingly effective for compilers and compiler-like things. Maybe because of its simplicity, I haven’t seen the basic technique in many compiler courses—or anywhere else in a CS curriculum for that matter. This post is an introduction to the idea and its many virtues.

Arenas or regions mean many different things to different people, so I’m going to call the specific flavor I’m interested in here data structure flattening. Flattening uses an arena that only holds one type, so it’s actually just a plain array, and you can use array indices where you would otherwise need pointers. We’ll focus here on flattening abstract syntax trees (ASTs), but the idea applies to any pointer-laden data structure.

To learn about flattening, we’ll build a basic interpreter twice: first the normal way and then the flat way. Follow along with the code in this repository, where you can compare and contrast the two branches. The key thing to notice is that the changes are pretty small, but we’ll see that they make a microbenchmark go 2.4× faster. Besides performance, flattening also brings some ergonomics advantages that I’ll outline.

A Normal AST

Let’s start with the textbook way to represent an AST. Imagine the world’s simplest language of arithmetic expressions, where all you can do is apply the four basic binary arithmetic operators to literal integers. Some “programs” you can write in this language include 42, 0 + 14 * 3, and (100 - 16) / 2.

Maybe the clearest way to write the AST for this language would be as an ML type declaration:

type binop = Add | Sub | Mul | Div
type expr = Binary of binop * expr * expr
          | Literal of int

But for this post, we’ll use Rust instead. Here are the equivalent types in Rust:

enum BinOp { Add, Sub, Mul, Div }
enum Expr {
    Binary(BinOp, Box<Expr>, Box<Expr>),
    Literal(i64),
}

If you’re not a committed Rustacean, Box<Expr> may look a little weird, but that’s just Rust for “a plain ol’ pointer to an Expr.” In C, we’d write Expr* to mean morally the same thing; in Java or Python or OCaml, it would just be Expr because everything is a reference by default.¹

With the AST in hand, we can write all the textbook parts of a language implementation, like a parser, a pretty-printer, and an interpreter. All of them are thoroughly unremarkable. The whole interpreter is just one method on Expr:

fn interp(&self) -> i64 {
    match self {
        Expr::Binary(op, lhs, rhs) => {
            let lhs = lhs.interp();
            let rhs = rhs.interp();
            match op {
                BinOp::Add => lhs.wrapping_add(rhs),
                BinOp::Sub => lhs.wrapping_sub(rhs),
                BinOp::Mul => lhs.wrapping_mul(rhs),
                BinOp::Div => lhs.checked_div(rhs).unwrap_or(0),
            }
        }
        Expr::Literal(num) => *num,
    }
}

My language has keep-on-truckin’ semantics; every expression eventually evaluates to an i64, even if it’s not the number you wanted.²

For extra credit, I also wrote a little random program generator. It’s also not all that interesting to look at; it just uses a recursively-increasing probability of generating a literal so it eventually terminates. Using fixed PRNG seeds, the random generator enables some easy microbenchmarking. By generating and then immediately evaluating an expression, we can measure the performance of AST manipulation without the I/O costs of parsing and pretty-printing.

You can check out the relevant repo and try it out:

$ echo '(29 * 3) - 9 * 5' | cargo run
$ cargo run gen_interp  # Generate and immediately evaluate a random program.

Flattening the AST

The flattening idea has two pieces:

• Instead of allocating Expr objects willy-nilly on the heap, we’ll pack them into a single, contiguous array.
• Instead of referring to children via pointers, Exprs will refer to their children using their indices in that array.

Let’s look back at the doodle from the top of the post. We want to use a single Expr array to hold all our AST nodes. These nodes still need to point to each other; they’ll now do that by referring to “earlier” slots in that array. Plain old integers will take the place of pointers.

If that plan sounds simple, it is—it’s probably even simpler than you’re thinking. The main thing we need is an array of Exprs. I’ll use Rust’s newtype idiom to declare our arena type, ExprPool, as a shorthand for an Expr vector:

struct ExprPool(Vec<Expr>);

To keep things fancy, we’ll also give a name to the plain old integers we’ll use to index into an ExprPool:

struct ExprRef(u32);

The idea is that, everywhere we previously used a pointer to an Expr (i.e., Box<Expr> or sometimes &Expr), we’ll use an ExprRef instead. ExprRefs are just 32-bit unsigned integers, but by giving them this special name, we’ll avoid confusing them with other u32s. Most importantly, we need to change the definition of Expr itself:

 enum Expr {
-    Binary(BinOp, Box<Expr>, Box<Expr>),
+    Binary(BinOp, ExprRef, ExprRef),
     Literal(i64),
 }

Next, we need to add utilities to ExprPool to create Exprs (allocation) and look them up (dereferencing). In my implementation, these little functions are called add and get, and their implementations are extremely boring. To use them, we need to look over our code and find every place where we create new Exprs or follow a pointer to an Expr. For example, our parse function used to be a method on Expr, but we’ll make it a method on ExprPool instead:

-fn parse(tree: Pair<Rule>) -> Self {
+fn parse(&mut self, tree: Pair<Rule>) -> ExprRef {

And where we used to return a newly allocated Expr directly, we’ll now wrap that in self.add() to return an ExprRef instead. Here’s the match case for constructing a literal expression:

 Rule::number => {
     let num = tree.as_str().parse().unwrap();
-    Expr::Literal(num)
+    self.add(Expr::Literal(num))
 }

Our interpreter gets the same treatment. It also becomes an ExprPool method, and we have to add self.get() to go from an ExprRef to an Expr we can pattern-match on:

-fn interp(&self) -> i64 {
+fn interp(&self, expr: ExprRef) -> i64 {
-    match self {
+    match self.get(expr) {

That’s about it. I think it’s pretty cool how few changes are required—see for yourself in the complete diff. You replace Box<Expr> with ExprRef, insert add and get calls in the obvious places, and you’ve got a flattened version of your code. Neat!

But Why?

Flattened ASTs come with a bunch of benefits. The classic ones most people cite are all about performance:

1. Locality. Allocating normal pointer-based Exprs runs the risk of fragmentation. Flattened Exprs are packed together in a contiguous region of memory, which is good for spatial locality. Your data caches will work better because Exprs are more likely to share a cache line, and even simple prefetchers will do a better job of predicting which Exprs to load before you need them. A sufficiently smart memory allocator might achieve the same thing, especially if you allocate the whole AST up front and never add to it, but using a dense array removes all uncertainty.
2. Smaller references. Normal data structures use pointers for references; on modern architectures, those are always 64 bits. After flattening, you can use smaller integers—if you’re pretty sure you’ll never need more than 4,294,967,295 AST nodes, you can get by with 32-bit references, like we did in our example. That’s a 50% space savings for all your references, which could amount to a substantial overall memory reduction in pointer-heavy data structures like ASTs. Smaller memory footprints mean less bandwidth pressure and even better spatial locality. And you might save even more if you can get away with 16- or even 8-bit references for especially small data structures.
3. Cheap allocation. In flatland, there is no need for a call to malloc every time you create a new AST node. Instead, provided you pre-allocate enough memory to hold everything, allocation can entail just bumping the tail pointer to make room for one more Expr. Again, a really fast malloc might be hard to compete with—but you basically can’t beat bump allocation on sheer simplicity.
4. Cheap deallocation. Our flattening setup assumes you never need to free individual Exprs. That’s probably true for many, although not all, language implementations: you might build up new subtrees all the time, but you don’t need to reclaim space from many old ones. ASTs tend to “die together,” i.e., it suffices to deallocate the entire AST all at once. While freeing a normal AST entails traversing all the pointers to free each Expr individually, you can deallocate a flattened AST in one fell swoop by just freeing the whole ExprPool.

I think it’s interesting that many introductions to arena allocation tend to focus on cheap deallocation (#4) as the main reason to do it. The Wikipedia page, for example, doesn’t (yet!) mention locality (#1 or #2) at all. You can make an argument that #4 might be the least important for a compiler setting—since ASTs tend to persist all the way to the end of compilation, you might not need to free them at all.

Beyond performance, there are also ergonomic advantages:

1. Easier lifetimes. In the same way that it’s easier for your computer to free a flattened AST all at once, it’s also easier for humans to think about memory management at the granularity of an entire AST. An AST with n nodes has just one lifetime instead of n for the programmer to think about. This simplification is quadruply true in Rust, where lifetimes are not just in the programmer’s head but in the code itself. Passing around a u32 is way less fiddly than carefully managing lifetimes for all your &Exprs: your code can rely instead on the much simpler lifetime of the ExprPool. I suspect this is why the technique is so popular in Rust projects. As a Rust partisan, however, I’ll argue that the same simplicity advantage applies in C++ or any other language with manual memory management—it’s just latent instead of explicit.
2. Convenient deduplication. A flat array of Exprs can make it fun and easy to implement hash consing or even simpler techniques to avoid duplicating identical expressions. For example, if we notice that we are using Literal expressions for the first 128 nonnegative integers a lot, we could reserve the first 128 slots in our ExprPool just for those. Then, when someone needs the integer literal expression 42, our ExprPool don’t need to construct a new Expr at all—we can just produce ExprRef(42) instead. This kind of game is possible with a normal pointer-based representation too, but it probably requires some kind of auxiliary data structure.

Performance Results

Since we have two implementations of the same language, let’s measure those performance advantages. For a microbenchmark, I randomly generated a program with about 100 million AST nodes and fed it directly into the interpreter (the parser and pretty printer are not involved). This benchmark is not very realistic: all it does is generate and then immediately run one enormous program. Some caveats include:

• I reserved enough space in the Vec<Expr> to hold the whole program; in the real world, sizing your arena requires more guesswork.
• I expect this microbenchmark to over-emphasize the performance advantages of cheap allocation and deallocation, because it does very little other work.
• I expect it to under-emphasize the impact of locality, because the program is so big that only a tiny fraction of it will fit the CPU cache at a time.

Still, maybe we can learn something.

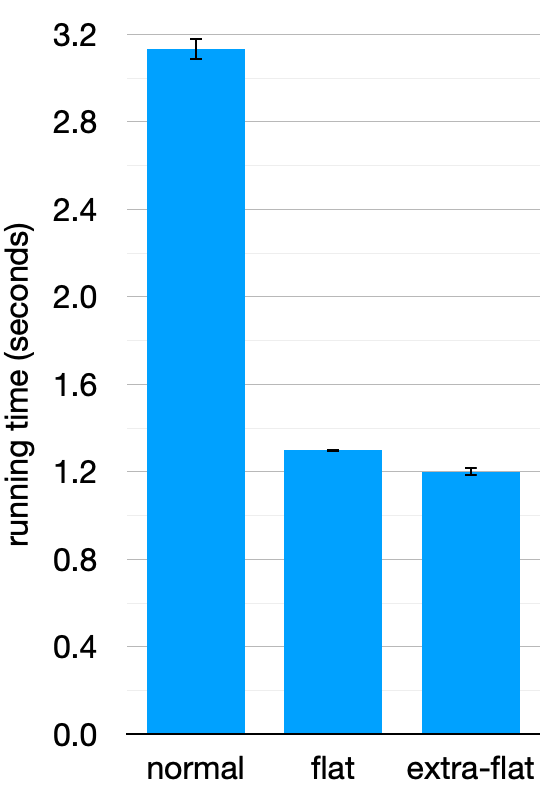
I used Hyperfine to compare the average running time over 10 executions on my laptop.³ Here’s a graph of the running times (please ignore the “extra-flat” bar; we’ll cover that next). The plot’s error bars show the standard deviation over the 10 runs. In this experiment, the normal version took 3.1 seconds and the flattened version took 1.3 seconds—a 2.4× speedup. Not bad for such a straightforward code change!

Of that 2.4× performance advantage, I was curious to know how much comes from each of the four potential advantages I mentioned above. Unfortunately, I don’t know how to isolate most of these effects—but #4, cheaper deallocation, is especially enticing to isolate. Since our interpreter is so simple, it seems silly that we’re spending any time on freeing our Exprs after execution finishes—the program is about to shut down anyway, so leaking that memory is completely harmless.

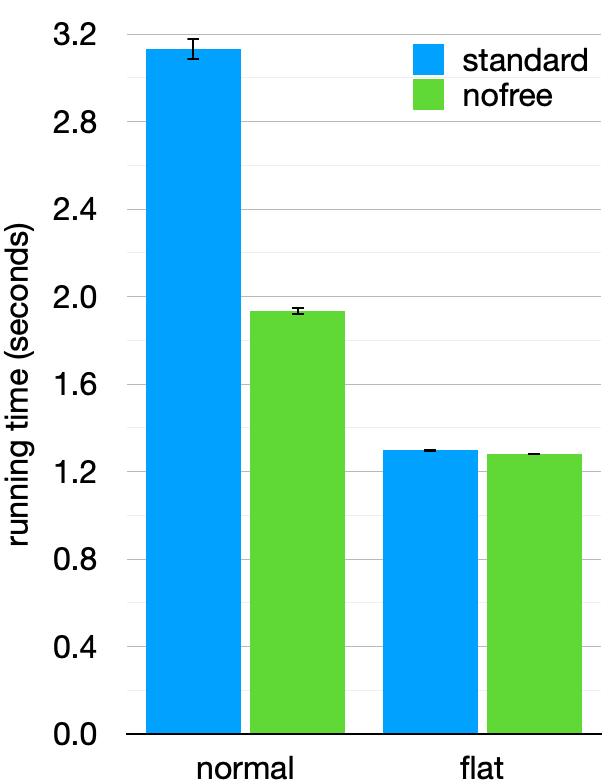
So let’s build versions of both of our interpreters that skip deallocation altogether⁴ and see how much time they save. Unsurprisingly, the “no-free” version of the flattened interpreter takes about the same amount of time as the standard version, suggesting that it doesn’t spend much time on deallocation anyway. For the normal interpreter, however, skipping deallocation takes the running time from 3.1 to 1.9 seconds—it was spending around 38% of its time just on freeing memory!

Even comparing the “no-free” versions head-to-head, however, the flattened interpreter is still 1.5× faster than the normal one. So even if you don’t care about deallocation, the other performance ingredients, like locality and cheap allocation, still have measurable effects.

Bonus: Exploiting the Flat Representation

So far, flattening has happened entirely “under the hood”: arenas and integer offsets serve as drop-in replacements for normal allocation and pointers. What could we do if we broke this abstraction layer—if we exploited stuff about the flattened representation that isn’t true about normal AST style?

The idea is to build a third kind of interpreter that exploits an extra fact about ExprPools that arises from the way we built it up. Because Exprs are immutable, we have to construct trees of them “bottom-up”: we have to create all child Exprs before we can construct their parent. If we build the expression a * b, a and b must appear earlier in their ExprPool than the * that refers to them. Let’s bring that doodle back again: visually, you can imagine that reference arrows always go backward in the array, and data always flows forward.

Let’s write a new interpreter that exploits this invariant. Instead of starting at the root of the tree and recursively evaluating each child, we can start at the beginning of the ExprPool and scan from left to right. This iteration is guaranteed to visit parents after children, so we can be sure that the results for subexpressions will be ready when we need them. Here’s the whole thing:

fn flat_interp(self, root: ExprRef) -> i64 {
    let mut state: Vec<i64> = vec![0; self.0.len()];
    for (i, expr) in self.0.into_iter().enumerate() {
        let res = match expr {
            Expr::Binary(op, lhs, rhs) => {
                let lhs = state[lhs.0 as usize];
                let rhs = state[rhs.0 as usize];
                match op {
                    BinOp::Add => lhs.wrapping_add(rhs),
                    BinOp::Sub => lhs.wrapping_sub(rhs),
                    BinOp::Mul => lhs.wrapping_mul(rhs),
                    BinOp::Div => lhs.checked_div(rhs).unwrap_or(0),
                }
            }
            Expr::Literal(num) => num,
        };
        state[i] = res;
    }
    state[root.0 as usize]
}

We use a dense state table to hold one result value per Expr. The state[i] = res line fills this vector up whenever we finish an expression. Critically, there’s no recursion—binary expressions can get the value of their subexpressions by looking them up directly in state. At the end, when state is completely full of results, all we need to do is return the one corresponding to the requested expression, root.

This “extra-flat” interpreter has two potential performance advantages over the recursive interpreter: there’s no stack bookkeeping for the recursive calls, and the linear traversal of the ExprPool could be good for locality. On the other hand, it has to randomly access a really big state vector, which could be bad for locality.

To see if it wins overall, let’s return to our bar chart from earlier. The extra-flat interpreter takes 1.2 seconds, compared to 1.3 seconds for the recursive interpreter for the flat AST. That’s marginal compared to how much better flattening does on its own than the pointer-based version, but an 8.2% performance improvement ain’t nothing.

My favorite observation about this technique, due to a Reddit comment by Bob Nystrom, is that it essentially reinvents the idea of a bytecode interpreter. The Expr structs are bytecode instructions, and they contain variable references encoded as u32s. You could make this interpreter even better by swapping out our simple state table for some kind of stack, and then it would really be no different from a bytecode interpreter you might design from first principles. I just think it’s pretty nifty that “merely” changing our AST data structure led us directly from the land of tree walking to the land of bytecode.

Further Reading

I asked on Mastodon a while back for pointers to other writing about data structure flattening, and folks really came through (thanks, everybody!). Here are some other places it came up in a compilers context:

• Mike Pall attributes some of LuaJIT’s performance to its “linear, pointer-free IR.” It’s pointer-free because it’s flattened.
• Concordantly, a blog post explaining the performance of the Sorbet type-checker for Ruby extols the virtues of using packed arrays and replacing 64-bit pointers with 32-bit indices.
• The Oil shell project has a big collection of links all about “compact AST representation,” much of which boils down to flattening.

Beyond just language implementation, similar concepts show up in other performance-oriented domains. I admit that I understand this stuff less, especially the things from the world of video games:

• A line of work from Purdue and Indiana is about compiling programs to operate directly on serialized data. Gibbon in particular is pretty much a translator from “normal”-looking code to flattened implementations.
• Flattening-like ideas appear a lot in data-oriented design, a broadly defined concept that I only partially understand. For example, Andrew Kelley argues in a talk on the topic for using indices in place of pointers.
• Check out this overview of arena libraries in Rust and its discussion of the ergonomics of arena-related lifetimes.
• Here’s a post comparing handles vs. pointers in game development that advocates for packing homogeneously typed objects into arrays and using indices to refer to them.
• Similar ideas show up in entity-component systems (ECS), a big idea from game development that I also don’t completely understand. This post covers many of the same locality-related themes as we did above.

After I published this post, many people pointed me toward a post from last year by Inanna Malick that shows the same technique applied to same kind of toy “calculator” language implemented in Rust. That post also uses recursion schemes, an elegant idea from the Haskell world that helps abstract over different concrete representations. I highly recommend checking that post out.