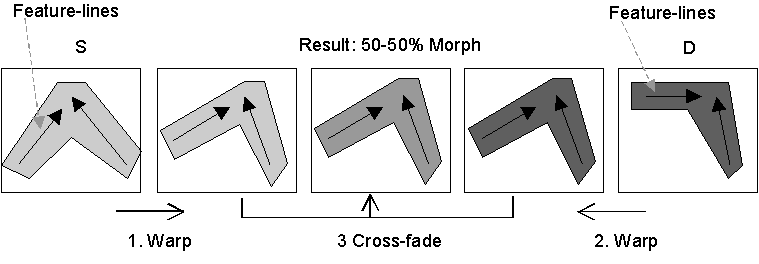
Figure 1. Beier and Neely morpher.
November 8-14, 1997
Crowne Plaza Hotel, Seattle, USA
We present a new technique for morphing two video sequences. Our approach extends still image metamorphosis techniques to video by performing motion tracking on the objects. Besides reducing the amount of user input required to morph two sequences by an order of magnitude, the additional motion information helps us to segment the image into foreground and background parts. By morphing these parts independently and overlaying the results, output quality is improved. We compare our approach to conventional motion image morphing techniques in terms of the quality of the output image and the human input required.
Image metamorphosis, video morphing, dense motion analysis
Video morphing, the process of creating a smooth, fluid transition between two objects in an image sequence, is a useful technique in cinematography. This technique was used extensively in the creation of the Michael Jackson video Black or White [PDI97], where video clips of the faces of 13 people singing were morphed from one person to the next. While the transitions looked realistic, several factors made them reasonably easy to create. Animators at Pacific Data Images used a plain, featureless background that was consistent among the sequences. Also, great care was taken to align the features of the faces in the source footage. Even with such careful camera work and editing, significant human effort was necessary to achieve smooth transitions. In this paper, we show how to use techniques from computer vision to reduce this effort.
Beier and Neely [Beier92] developed the algorithm used in Black or White. We review their algorithm in section The Beier and Neely algorithm . Their approach is primarily designed for still image morphing and requires the user to input a number of feature lines that define the correspondence between source and destination images. In practice, a large number of feature lines (10-100) are required to achieve a visually pleasing morph, leading to significant work for the animator. For example, if 25 feature-line pairs (50 lines, 100 points) must be specified for each frame of output, 4,800 points must be specified by the animator to create 2 seconds of morphed video at 24 frames per second.
Beier and Neely recognized this problem, and proposed linearly interpolating the feature lines between key frames when morphing video sequences. This technique only works well if the motion of the feature lines between key frames is linear. In practice, it is often non-linear, so that key frames must be defined every 2-6 frames (requiring 800 - 2,400 points for the above example).
In addition to specifying the feature set, image segmentation is often used to create visually pleasing morphs. That is, the foreground image is separated from the background image in each video frame. The parts are morphed independently, and the results combined using matting techniques [Porter84] to produce the output image. Beier and Neely used a painting program and segmented the video by hand [Beier92].
All together, the current process of creating high quality morphed video is labor intensive. Beier and Neely reported that a typical morphed sequence at Pacific Data Images requires about 3 weeks of animator design time, 75% of which is spent creating and tweaking the feature-line set [Beier92].
Our goal is to reduce the amount of user input required for video morphing, while improving the quality of the output. In this paper, we show how to use computer vision techniques to accomplish both objectives. In particular, we show how to:
Feature-line tracking reduces the number of frames that require the user to input feature lines. For short (1-2 second) sequences, the user must typically provide feature lines for only one frame of each sequence. We also require the user to divide these feature lines into groups, such that the motion of each group can be modeled with an affine transformation.
Once the feature lines are specified in a few key frames, our system computes the position of the feature lines in the intermediate frames as follows: we compute a dense motion field for the video sequence. The motion field is used to compute the best (in the least-squares sense) affine transformation for each feature-line group. We then apply the transformation to each group. We describe this algorithm in detail in section Feature line tracking .
In addition to automatically interpolating the position of the feature lines, we also automatically segment the video into foreground and background parts. While image segmentation is difficult (if not impossible) to perform on static images, segmenting an image sequence is possible [Smith92], [Smith95]. Our motion segmentation algorithm, given an image segmentation for frame It, automatically segments the next frame (It+1) by tracking the motion of the segments in It. The segmentation for one of the frames has to be provided by the user. The segmentation information is used to divide the image into component parts, each of which is morphed independently. We then composite the results to produce the output image. We sketch the major features of our segmentation algorithm in section Image Segmentation. A full description of the segmentation algorithm is available elsewhere [Ferencz].

Figure 1. Beier and Neely morpher.
The Beier and Neely morphing algorithm [Beier92] is primarily concerned with morphing still images. Still image morphing requires user input to position line segments over corresponding features in the source and destination images. It outputs a sequence of frames depicting a smooth transition from the source into the destination image. Their algorithm works as follows (see figure 1):
To morph video sequences, Beier and Neely propose a simple extension to their algorithm. The user is required to enter the feature lines only in key frames. The feature lines for the intermediate frames are computed by linearly interpolating their position from the surrounding key frames. Thus, the motion of the objects in the intermediate frames must conform to a rather strict assumption: it cannot deviate from linear. In practice, this restriction translates into requiring key frames every 2-6 frames for most video sequences.
Thus, the animator must draw feature lines in a high number of key frames to produce a smooth video morph, a tedious and time-consuming task. In order to reduce human input, we use techniques from computer vision to more accurately estimate the position of the feature lines in intermediate frames, reducing the number of key frames that must be entered by an order of magnitude. Using our system we were able to produce 1- to 2-second-long sequences of video morphing using feature lines from a single key frame.
Since the original feature-based morphing algorithm, some research has addressed the problem of reducing amount of user input in morphing. Lee et al. [Lee95] describe a technique for automating precise feature line placement by using energy minimizing contours (snakes). They assume that the feature lines are placed near image features (intensity edges). The animator is required to place only approximate feature lines. Those lines are then interpreted as the initial position of a snake. As the snake minimizes its energy, it gets closer to the intended feature line. Although the work does not explicitly state it, this approach could be used in video morphing, provided that the difference between consecutive frames is very small, so that the snake from one frame could be used as an input snake in the next frame.
Briefly, our algorithm for interpolating feature lines works as follows:
We describe these steps in the following sub-sections.
Grouping feature lines captures the idea that related lines move in a related manner. Modeling this motion with affine transformations allows us to describe any combination of translation, rotation, scale, and shear to a group of lines. The equations of affine transformations are:
![]()
![]()
We argue that this model allows us to describe arbitrary motion. When non-rigid objects are present and more complicated transformations are needed, we can form smaller groups which move independently. For example, consider a person standing still and waving an arm. While the motion of the entire person cannot be described with an affine transform, we can break up the motion into affine components, like the motion of the body, head, upper arm, and forearm. Each of those parts can be assigned a group of feature lines. In the limit, there will be only one line per group, and clearly an affine transformation can specify all the possible transformations of a line (two endpoints of the line will produce a system of 4 equations with 6 unknowns). But there is a price to pay for this freedom: nothing guarantees that lines in different groups will maintain any relation to each other. In our previous example, there is nothing to prevent the upper arm feature lines from drifting away from the forearm feature lines (resulting in a very long elbow in the output).
As objects move and rotate, parts of an object may appear or disappear during the sequence. When a region disappears, the feature lines associated with that region also shrink and disappear. When new areas appear, however, no feature lines are assigned to them. It is often possible to choose a frame in the sequence where most of the features of all the objects are visible. Therefore, it is often useful to allow the user to pick the frame to which features-lines are added (the key frame). For some sequences, such as one with a rotating object, however, the user may need to supply additional feature lines in other frames of the sequence, whenever new features appear.
Once the user has selected the key-frame(s) and added the feature lines, the tracking process will compute the location of these lines throughout the sequence. The tracking algorithm can be broken down into two parts: computing a dense motion field and using that motion field to fit a transform.
In order to estimate the affine transform for each group of feature lines, we need to compute the motion of the individual points in the image. This computation can be performed on every point or just on the points of interest (e.g., the endpoints of the feature lines). We decided to compute the motion field for the entire image (a dense motion field) to make the computation independent of the feature lines. This allows us to compute the motion once per sequence, and to use those results for many different morphs. By computing a dense motion field, morphing the sequence with a different group of feature lines will not require us to repeat the expensive motion computation, making experimentation with different placement of features relatively cheap.

Figure 2. 9 pixels from an image and the results of comparison against P.
To compute the motion vector for each pixel, we use a census transform [Woodfill94]. The n-bit census transform C(P) maps the pixel P into a set of n bits based on the intensity of nearby pixels. If the intensity of a nearby pixel is less than P, the bit is set to 1; otherwise it is set to 0. For example, for the image shown in figure 2, an 8-bit census transform would map pixel P to the bit string 010010011.
Let It be the tth image in the sequence I. We first compute a 32-bit census transform for each image in I. We then assign a motion vector to each pixel in image It. This motion vector is chosen by finding the closest 9x9 block of pixels in It+1 that minimizes the Hamming distance2 to the 9x9 block of pixels centered at P. To increase the efficiency of this process, we only search within a small window of pixels in It+1. We generally used a 20 by 20 search window (where each point in It can move up to 10 pixels in each direction in It+1) for most sequences. However, in sequences with rapid motion from frame to frame, we found that a larger window (32x32) is necessary.
The motion field computed above gives us a motion vector for each pixel in the image. This vector gives an estimate of how the point moves from frame to frame. Due to image noise and the inherent limitations of motion estimation, this data is not very reliable. In order to obtain a more reliable transform estimation, we find a transform which best describes (in the least-squares sense) the motions of related reference points.
To compute the transformation for the group of feature lines, we need to specify which motion vectors will be considered in the fitting. One extreme is to use just the vectors corresponding to the end-points of the feature lines. The other extreme is to base our estimates on the vectors from the area enclosed by the group of lines. The first approach will provide too few data points. The second approach is problematic, since a group of lines does not necessarily correspond to any a priori definable area (e.g., if a group consisted of two perpendicular lines, what area would they define?). Thus, we settled on an intermediate approach: we base our estimates on the motion of the pixels that fall on line segments in a given group.
Let I be a sequence of images and It be the tth
image in that sequence. We represent each line segment as the set of points P
falling on that segment. Given the backward motion field ![]() ,
where Q is a point, we find a set of mappings Z for the points in P:
,
where Q is a point, we find a set of mappings Z for the points in P:
![]() [Eq. 1]
[Eq. 1]
The set Z tells us, for all the points in P, the corresponding points in It+1. In other words, it gives us the motion of the feature-line from It to It+1. If the set Z is smaller than THRESH points, we say that the feature-line disappeared. In that case, we remove that feature-line from the group. Otherwise, the line exists.
Set Z might still be rather small (because of errors in motion
estimation, round-off errors, or an actual shortening of the line), making it unsuitable
for least-squares fitting. To enlarge the sample, we compute the forward motion field ![]() and augment Z with a set Z’:
and augment Z with a set Z’:
![]() [Eq. 2]
[Eq. 2]
Mappings from Z determine the existence of the line, while mappings from Z’ generate more data for the line estimation. We repeat that process for all the lines in a group, and take the union all of the resulting sets Z and Z’ to produce set U:
![]() [Eq. 3]
[Eq. 3]
The set U contains the mapping from points in the feature lines
in the image It to the points (presumably) in the feature lines in the
image It+1. Since we assumed that points in It+1 can be
computed from the points in It by application of some affine transform,
for every mapping ![]() , we create an equation d=sA, where
A is the affine transformation matrix. Those equations must be satisfied simultaneously.
Expanding matrices, we get
, we create an equation d=sA, where
A is the affine transformation matrix. Those equations must be satisfied simultaneously.
Expanding matrices, we get

We solve this system using the normal equations of the least-squares problem. The solution becomes

Since our motion field contains unreliable data, which can fool the least-squares fit, we compute the trimmed least squares. We compute the LS fit once to get an estimate of the transform, and again after the largest (worst 20%) of the outliers are eliminated. We transform the feature lines using the second fit.
After completing this processing for both the source and destination image sequences, we have computed feature lines for each frame in both sequences. We can use these feature lines to morph one sequence into the other frame by frame. However, we can make the output more visually pleasing if we segment the frames into foreground and background image, morph those images independently, and overlay the results. We describe our method for image segmentation in the next section.
In morphing, the animator wants to draw attention to the metamorphosis of one or more foreground object. If the background changes are too prominent, the visual impact of the morph is diluted. The same dilution occurs if there are too many foreground objects. Thus, image sequences that lend themselves to morphing usually feature a few dominant foreground objects and relatively similar backgrounds.
This consideration affects the distribution of the feature lines: their placement is concentrated on the foreground object. Although the influence of the feature lines drops off with distance, the foreground lines have a significant effect on the background, causing distortions in the otherwise static background. One way to compensate for this effect is to draw a number of "stabilizing" lines in the background. This, however, does not have the full desired effect because it simply introduces competing influence fields, rather than limiting the range of the foreground feature lines to the foreground object.
A better approach is to segment the image into foreground and background objects, morph the foreground objects, combine the backgrounds, and overlay the results. This idea is somewhat similar to the representing a video sequence with layers presented in [Wang94]. Segmenting the image can be accomplished manually (using a painting program) or automatically, using techniques from computer vision. In this section, we describe our approach to automatic image segmentation.
Although segmenting a static image is difficult, if not impossible, segmenting an image sequence is tractable because sequences provide motion information. Previous work has addressed foreground-background segmentation of image sequences. Smith [Smith92], [Smith95] provides an overview of current techniques. Available algorithms have proven effective for relatively simple scenes, such as those typically used in video morphing.
We make two assumptions about the sequences. First, we assume that the background is static throughout the sequence. This restriction can be relaxed by finding the mode of all motion vectors from one frame to the next, and translating the images to align them. For more complicated scenes, one could attempt to fit an affine transformation to the frames in order to align them [9].
Second, we assume that the user has identified the initial foreground-background segmentation on a key-frame of the sequence. This is necessary, as some parts of the foreground may be stationary throughout the sequence.
We use a segmentation algorithm based on RubberSheets [Ferencz]. While this method is not robust for complex scenes, it works well given the assumptions above, and has the advantage of often tracking the boundaries of the foreground object exactly.
A RubberSheet is a two-dimensional patch that represents the region of the image occupied by the foreground. The RubberSheet is moved from frame to frame based on internal and external energy functions. The internal energy function is a property of the sheet that defines the preferred shape, size, and edge smoothness of the sheet. For segmenting video sequences, the internal energy function is chosen to conserve sheet area and edge smoothness. The external energy function is a property of the image sequence that provides an energy value for each pixel of an image. Low values of this function attract the sheet; high values repel it. The RubberSheet moves to minimize the sum of the internal and the external energy under the sheet.
The external energy map is a two dimensional array that has the same dimensions as It. Let P be the set of pixels that are part of the sheet in frame It-1. We calculate the set U of motion vectors originating from the pixels in P (i.e., we calculate U using equation 3). We then calculate each element m in the energy map as follows:
The intuition behind this energy function is to assign low values to the energy function for points where the RubberSheet moves according to the motion field. We further decrease the energy of pixels where the image difference exceeds a threshold to further pull the sheet towards parts of the image that are in motion.
The internal energy of the sheet is calculated using three factors:
With these constraints, the RubberSheet uses a simulated annealing algorithm to calculate the position of the sheet in It that minimizes the total of the internal and external energy functions. The sheet that results defines the segmentation for frame It+1, which, in turn, is used as the input for the segmentation of frame It+2.
The product of the segmentation algorithm is a map (a binary image) for each frame indicating which pixels are in the foreground and which are in the background. We run this algorithm on the source and destination image sequences I and J (T frames each) to produce 2*T maps (IF and JF).
 |
 |
Figure 3. The first frame from the source sequence and the reconstructed
background.
We use the binary maps IF and JF to partition each image in the image sequences into foreground and background components. We morph each part using the Beier and Neely algorithm and overlay the results. With this scheme, step 1 in figure 1 is expanded into 3 warps and one overlay, as shown in figure 4.
To construct a composite background, we paste together areas of the images that the segmentation algorithm found to be the background. While this method tries to find each pixel of the background in the sequence, it is possible that some regions were never exposed during the sequence (i.e., the foreground always covered them). Due to the warping effects of morphing, some small portions of these hidden areas may become exposed. As we have no direct information about these regions, we must extrapolate from the surrounding known areas. An example of such a reconstructed background is shown in figure 3. From such backgrounds (one for I and one for J), we generate a still morph sequence BG of length T that morphs one background into the other.

Figure 4. Use of mask and segmentation.
To compute the foreground, we use the Beier and Neely algorithm to morph the original images It and Jt and the binary maps IFt and JFt using only those lines attached to the foreground. This computation produces image F from It and Jt and a mask MF from IFt and JFt. In order to produce the final image, we overlay the morphed foreground F on top of the morphed background BGt using the mask MF.
To summarize, our algorithm is given as input two sequences I and J of length T, a group of background feature lines D, and n groups of foreground feature lines F0…Fn (defined in a key frame). It outputs a sequence M that is a morphed transition between the first frame of I and the last frame of J. Our algorithm proceeds as follows:




Figure 5. Feature lines tracked by the algorithm. Frames 4, 8, 12 and 16.
We compared the effectiveness of our approach to the Beier and Neely morpher. Figure 5 shows frames from two 17 frame sequences with Rob (left column) and Henry (right column). Feature lines were drawn on the initial image in each sequence, and the rest of the feature lines shown were generated automatically by the tracker. Note that feature lines stay attached to their features for the duration of the sequence.
Figures 6 through 9 show the output of our morpher (figure 7) and the output of the Beier and Neely morpher (figure 8). The static morphs were generated by manually drawing the feature lines for each frame in the sequence. Comparison of the background of the middle frames of each sequence shows that the foreground-background segmentation significantly improves the quality of the resulting morph.

Figure 6. I0: Rob. The initial picture in the sequence.
 |
 |
 |
 |
 |
 |
| Figure 7. Frames 4, 8, and 12 generated automatically by our algorithm. Full video available here | Figure 8. Frames 4, 8, and 12 generated manually by Beier/Neely still morphing algorithm. |

Figure 9. J16: Henry. The final frame of the sequence.
Figure 10. Another video morphing sequence.
On a Pentium-150 machine with 48 MB of memory, the computation of the motion field on a 320 by 240 pixel image with a 20x20 search window requires about 30 seconds per frame, and the segmentation of the image requires about 10 seconds per frame. Compared to these costs, the cost of morphing the frames and computing the optimal affine transforms is minimal. Since these calculations can be performed in the background while the user is defining the feature lines and since they only need to be performed once per sequence, these costs may not seriously affect the time required to create a smooth morphing sequence.
We have presented an algorithm for morphing two video sequences. Our algorithm improves on previous work by using techniques from computer vision to automate the production of feature lines and the segmentation of the images. This automation reduces the amount of human effort required to produce high quality morphs by an order of magnitude: our tests show that morphing 2 second sequences is possible with a single key frame, whereas the method of linear interpolation would use about 8 key frames.
The assumption that the two sequences are the same length could be relaxed. In order to make the sequences the same length, we could either throw out frames from the longer sequence or generate more frames for the shorter sequence. Morphing adjacent frames of that sequence together can produce these missing frames.
This observation also suggests that this technique could be used for video frame rate conversion, similar to 3:2 pull-down [Jack96] but without interlacing artifacts.
It should be noted that both the morphing and the segmentation algorithm could be replaced with other variants. Since our algorithm depends on the underlying image morpher, almost any improvements to still morphing techniques will benefit the quality of the images. Since our algorithm makes very few assumptions about the underlying morpher, it can be viewed as a framework that can be used with any still morphing algorithm.
[ 1] In this example, the order of comparison is left to right, top to bottom. The order is arbitrary, but a consistent order must be used.
[ 2] The Hamming distance is the number of bits that differ in two bit sequences.
Our implementation of the underlying still image morpher is based on WLAMorph written by Scott Cytacki at Cornell University, 1995.