|

| |
Enhancement of a Mathematical Computing Environment
For the last decade, the Cornell mathematics department has been a leader in research
which has been aided by computation-intensive computer programs. To continue to do
ground-breaking work, we must use the most powerful equipment available. The research we
will conduct includes:
Hybrid Systems Research: Derive digital control programs for distributed
autonomous systems (such as network routing, highway and air control, distributed
simulation) from mathematical models and methods of relaxed variational calculus on
differentiable manifolds constructed to describe the problems.
|
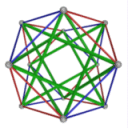
Stability of Symmetric Tensegrity Structures: Study structures to
determine geometric conditions that imply stability. We plan to calculate and make widely
available a catalog of stable tensegrity structures that would be of use to architects and
sculptors, as well as engineers. Preliminary calculations in Maple and on an IRIS
workstation indicate that there are over a hundred essentially different families of such
structures that have the rotational symmetry of the regular dodecahedron alone. |
A Universal Finite Element Mesh Strategy for Optimal Numerical Resolution of a Class
of Physical Problems with Power Type Singularities: There are extremely important
classes of physical problems whose resolution requires the solution of partial
differential equations. As a few examples we mention problems in structural mechanics,
thermodynamics, semiconductor simulation, fluid dynamics and electricity and magnetism. We
will investigate a new theory which we believe will yield optimal approximations, in fact
even superconvergent approximations, and at the same time greatly simplify the solution
process for certain important classes of these problems.
Participants
 | Robert Connelly, Chair, Mathematics Department |
Web Links
|
