To a physicist, water at room temperature is not terribly interesting. Neither is ice at 20 below. But the transition that occurs from one phase to the other at 0C now that's something to behold. The natural world is full of such phase transitions. Crystals reconfigure themselves as pressure or temperature changes. Biological systems can undergo snap transformations. And now it looks as though the same sort of thing happens in mathematical logic, as Scott Kirkpatrick of the IBM Watson Research Center in Yorktown Heights, New York, and Bart Selman of AT&T Bell Laboratories report in this issue.

On page 1297, they show that when randomly generated assertions are strung together to form longer and longer "logical statements," the statements switch suddenly from being almost always true to being almost always false. By borrowing techniques from physics, Kirkpatrick and Selman were able to parlay their empirical results into predictions about where these "phase changes" occur in entire classes of statements. Such predictions may be important, the researchers argue, because the difficulty of checking a statement's truth --- its computational complexity --- rises to a peak just at the transition.

Phase transitions and the computational complexity they bring may help explain why artificial intelligence programs sometimes bog down. They may even have implications beyond logic, explaining some of the computational difficulty of the "hard" problems found throughout computer science, says Tad Hogg at the Xerox Palo Alto Research Center. The phase-transition viewpoint, he says, provides a general approach "that you could use on lots of problems. It's too early to claim that it actually works, but it has the potential for that. "

The logical statements in Kirkpatrick and Selman's study take the form of Boolean expressions (named after the nineteenth century mathematician George Boole), in which variables such as x and y represent simple statements such as "it is raining" or "I'm wearing a raincoat," which must be either true or false. Boolean expressions are created by combining logical variables with ANDs, ORs, and NOTs. For example, the logical statement "either it's not raining, or else I'm wearing a raincoat" can be written as "-x OR y," where "-x" stands for "NOT x."

A Boolean expression is called "satisfiable" if the variables in it can be assigned the values true and false in such a way as to make the entire statement true. Thus "-x OR y" is satisfiable because it is true when, for example, x is true --- so that -x is false --- and y is true as well, leaving one true alternative. Short expressions are usually satisfiable, but longer, more complicated ones, in which the same variable may appear many times in different contexts, often are not.

Kirkpatrick and Selman's study focuses on the satisfiability of Boolean expressions in what is known as conjunctive normal form --- a format into which every Boolean expression can be converted. An expression in this form consists of a set of clauses, each made up of a series of variables linked by ORs, so that only one variable needs to be true for the clause to be true. The clauses, however, are linked by ANDs, which means they all have to be true for the entire statement to be true. Checking such an expression's satisfiability, says Selman, is a way to test whether a given set of inputs is open to a consistent interpretation. "[Satisfiability] lies at the core of a lot of reasoning tasks in artificial intelligence."

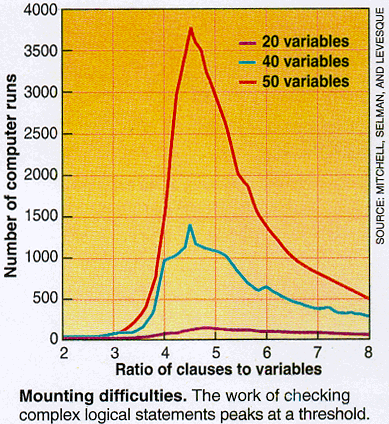
That kind of checking entails testing different truth assignments for the variables to see if any combination makes the expression true. The difficulty of the task increases in a smooth, exponential relation to the number of variables. But another factor --- the ratio of the number of clauses to the number of different variables --- has a different effect, as Selman found in an earlier computer experiment with Hector Levesque at the University of Toronto and David Mitchell at Simon Fraser University in Burnaby, Canada.

Testing the satisfiability of randomly constructed Boolean expressions that had different clause-to-variable ratios, they found that their algorithms ran quickly on problems with either small or large ratios, even though the outcome was different: When the ratio was small, almost all expressions were satisfiable, whereas almost none were when the ratio was large. In between --- at a ratio of around 4.2 for expressions that had clauses three variables long --- lay a transition from satisfiable to unsatisfiable, and it was there that the longest run times clustered.
 

Selman and Kirkpatrick say that this transitional behavior, which they have now confirmed in additional computer uns, isn't surprising. Loosely speaking, statements with few clauses are too short to contradict themselves, whereas long statements, if generated at random, invariably contain contradictions that are easy to spot. It's only in the middle ground where contradictions can arise but be difficult to find. But the transition's sharpness is a surprise. And the group now has evidence that such transitions are ubiquitous in Boolean systems. The key to their argument is a tantalizing analogy that Kirkpatrick, an expert in statistical physics, draws between logical thresholds and phase transitions in so-called spin glasses.

A spin glass, a kind of idealized magnetic material created in computer simulations, consists of a multitude of magnetic particles whose magnetic axes point at random at high temperatures but undergo a phase transition to a more ordered state as the material is cooled. The ordering is often incomplete, however. For the material to reach its lowest energy state, each particle has to have a specific orientation with respect to its neighbors, but this constraint often can't be satisfied throughout the spin glass. ''Frustrated'' regions, where the orientations can't be reconciled, are the result.

To Kirkpatrick, that phase transition mirrors the shift from satisfiable to unsatisfiable in Boolean statements. As in frustrated spin glasses, small groups of clauses in an unsatisfiable expression can be made simultaneously true, but large clusters often contain contradictions. On the strength of that analogy, Kirkpatrick and Selman applied a highly successful technique for studying phase transitions, called finite-size scaling, to extend their experimental results to logical statements of arbitrarily large size with anywhere from three to six variables per clause, fuming up phase transitions everywhere.

Kirkpatrick and Selman expect their techniques to raise eyebrows among some mathematicians. "Finite-size scaling is not a rigorous mathematical model," Selman points out. But at the very least, says Hogg, the analogy with statistical physics gives researchers "a very, very different viewpoint" for thinking about other problems that tend to use up inordinate amounts of computer time. It might even seed a phase change in the field.

--- Barry Cipra

p. 1249