Sequents to typing judgments

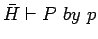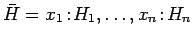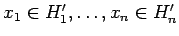We can now translate deductions of sequents $\bar{H} \vdash P\ by\ p$ to derivations of $[\![\bar{H}]\!] \vdash [\![p]\!] \in [\![P]\!]$. Given $\bar{H} = x_1\!:\!H_1, \ldots, x_n\!:\!H_n$ we take $[\![\bar{H}]\!]$ to be $x_1 \in H'_1, \ldots, x_n \in H'_n$ where if H_i is a type then H'_i = H_iand if H_i is a formula then $H'_i = [\![H_i]\!]$. In this case we treat the label x_i as a variable.

Now to translate a deduction tree to a derivation tree we work up from the leaves translating sequents as prescribed and changing the rule names. The proof system was designed in that we need not change the variable names.