


Next: A semantics of proofs
Up: Using type systems to
Previous: Using type systems to
The meaning of
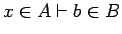 is that A is a type and for any two
elements, a, a' of A, B[a/x] is a type and
B[a/x]=B[a'/x] (i.e. B is
type functional in A), and moreover,
is that A is a type and for any two
elements, a, a' of A, B[a/x] is a type and
B[a/x]=B[a'/x] (i.e. B is
type functional in A), and moreover,
![$b[a/x] \in B[a/x]$](img719.gif) and
b[a/x]=b[a'/x] in B[a/x]. We have extended this notion to multiple
hypotheses inductively to define
and
b[a/x]=b[a'/x] in B[a/x]. We have extended this notion to multiple
hypotheses inductively to define
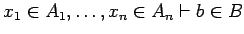 .
This definition can be carried over to type systems.
.
This definition can be carried over to type systems.
James Wallis
1999-09-17