Universes

universe

We can consider U₁ and the rules for it in the last section as partial axiomatization of the concept of Type. On this view, we think of U₁ as open-ended, and we do not adapt an axiom capturing its closed inductive character, such as the recursion combinator for U₁ discussed above.

On the other hand, we can also think of U₁ as a large type belonging to Type. On this view the axioms for U₁ reflect the rules of type construction on Type into the collection of types. The axioms postulate a certain enrichment of the concept Type in the same way that the axiom of inaccessible cardinals postulates an enrichment of Set. Similarly, from the foundations of category theory ([68]), Grothendieck's concept of a universe is a way of modeling large categories (and is equivalent to inaccessible cardinals).

If we take the view that U₁ is a universe (rather than Type), then it makes sense to form larger universes, say U₂, then U₃, etc. To form U₂ we extend U₁ by adding the type U₁ itself, like this: $\ \ \ \ U_1 = U_1\ \mbox{in}\ U_2$.

Martin-Löf and Nuprl axiomatize a universe hierarchy indexed by natural numbers, U_i. The method of doing this is to add U_i = U_i to U_i+1and to postulate cumulativity, that any type A in U_i belongs to all U_j for i<j. So the universe rules universe rules are:

$$U_i = U_i\ \mbox{in}\ U_{i+1}\ \ \ \ \ \ \ \ \ \ \frac{A = A\ \mbox{in}\ U_i}{A = A\ \mbox{in}\ U_j\ \ \ \mbox{for}\ i<j.}$$

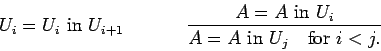
It is possible to extend the universe hierarchy further, say indexed by ordinal numbers ord. It is possible to postulate closure of Type under various schemes for generating larger universes; [92] considers such matters.

Nuprl has been designed to facilitate index free, or ``polymorphic''polymorphic, treatment of U_i. Generally, the user simply writes a universe as U_i and the system keeps track of providing relative level numbers among them in terms of expressions called level expressions which allow forming i+1 and max(i, j). The theoretical basis for this is in [3] and was implemented by Howe and Jackson (see [66]).