Essential features

In this section I want to give a nontechnical overview of the subject I am calling type theory. I will discuss these points:

• It is a foundational theory in the sense of providing definitions of the basic notions in logic, mathematics, and computer science in terms of a few primitive concepts.
• It is a computational theory in the sense that among the primitive built-in concepts are notions of algorithm, data type, and computation. Moreover these notions are so interwoven into the fabric of the theory that we can discuss the computational aspects of every other idea in the theory. (The theory also provides a foundation for noncomputational mathematics, as we explain later.)
• It is referential in the sense that the terms denote mathematical objects. The referential nature of a term in a type T is determined by the equality relation associated with T, written 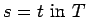$s=t\ \mbox{in}\ T$. The equality relation is basic to the meaning of the type. All terms of the theory are functional over these equalities.
• When properly formalized and implemented, the theory provides practical tools for expressing, performing, and reasoning about computation in all areas of mathematics.

A detailed account of these three features will serve to explain the theory. Understanding them is essential to seeing its dynamics. In a sense, the axioms of the theory serve to provide a very abstract account of mathematical data, its transformation by effective procedures, and its assembly into useful knowledge. I summarized my ideas on this topic in [31].