Lists

list

Sequences are basic forms of construction in mathematics, often written $(a_1, \ldots, a_n)$. With the widespread use of programming languages we have come to distinguish several data types associated with sequences as distinct types. There are lists, arraysarray, and sequencessequence, and they have different mathematical properties. We first look at lists.

If A is a type, then so is A list. We could write an informal rule like this

$$\frac{A \in Type}{A\:list \in Type}.$$

The elements of an A list are nil and (a. l) where $a \in A$ and $l \in A$ list. If A is ${{\mathbb{N} }}$, these are lists:

$$nil\ \ \ \ \ (2.\: nil) \ \ \ \ \ (1.\: (2.\: nil))$$

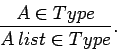
All lists are built up from nil and the operation of pairing an element of A with a list. The typing rules are

$\bar{H} \vdash nil \in A\:list \ \ \ \ type\_of\_nil \ \ \ \ \ \ \ \bar{H} \vdash (a.\: l) \in A\:list \ \ \ \ type\_of\_cons$

                                                          $\bar{H} \vdash a \in A$

                                                          $\bar{H} \vdash l \in A\:list$

Equality on lists is given by these rules.

$\bar{H} \vdash (h.\ t) = (h'.\ t')$ in $A\:list$ by list-eq

       $\bar{H} \vdash h=h'$ in A

       $\bar{H} \vdash t = t'$ in $A\:list$

$\bar{H} \vdash nil = nil$ in $A\:list$. by nil-eq

For every type A, A list is an inductive type with base case of nil. The inductive character of the type is given by its induction rule stated below for $P \in (A\ \mbox{list} \times T \Rightarrow\ Prop)$

$\bar{x}\!:\!\bar{H}, l\!:\!A\:list \vdash P(l, \bar{x})\ \mbox{by} \ list\_ind\:(l; p_o; h, t, i.\: p(h, t, i, \bar{x}))$

$\bar{x}\!:\!\bar{H}$ $\vdash P(nil, \bar{x})\ \mbox{by}\ p_o$

$\bar{x}\!:\!\bar{H}, l\!:\!A\:list, h\!:\!A, t\!:\!A\:list, i\!:\!P(t, \bar{x}) \vdash P((h.\:t), \bar{x})\ \mbox{by}\ p(h, t, i, \bar{x})$

We can define the usual head-and-tail head tail functions by induction. Define $Compound(x) == \exists h\!:\!A.\ \exists t\!:\!A\:list.\ x=(h.\ t)$ in $A\:list$.

$\vdash \forall x\!:\!A\:list.\ (x=nil$ in $A\:list\ \vee \ Compound(x))$

by $\forall\!R$

$x\!:\!A\:list \vdash (x=nil$ in $A\:list\ \vee \ Compound(x))$

          by $list\_ind$

           $\vdash nil=nil$ in $A\:list\ \vee\ Compound(x)$

          by VRl

    $x\!:\!A\:list, h\!:\!A, t\!:\!A\:list \vdash (h.\ t) = nil$ in $A\:list \vee Compound(h.\ t))$

                    by VRr

                     $\vdash \exists h'\!:\!A.\ \exists t'\!:\!A\:list.\ (h.\ t) = (h'.\ t')$ in $A\:list$.

                    by $\exists R\: h\:$ THEN $\exists R\: t$

We can also prove

$$\vdash \forall x\!:\!A\:list.\ \exists ! h\!:\!A.\ \exists ! ... ...neg (x=nil) \Rightarrow x=(h.\ t)\ \mbox{in}\ A\:list\right)$$

where $\exists !$ expresses unique existence (see the end of section 2.9).