


Next: Types
Up: Propositions
Previous: The category of propositions,
propositional function
Frege's analysis of propositions into functions and arguments is central to
modern logic. It requires us to consider the notion of a propositional
function. Frege starts with concrete propositions such as 0 < 1, then
abstracts with respect to a term to obtain a form like 0 < x which denotes a
function in x. In Principia notation, given a proposition 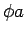 ,
,
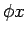 is the ambiguous value, and the propositional function is
is the ambiguous value, and the propositional function is
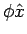 ;
so 0 < 1 can be factored as
;
so 0 < 1 can be factored as 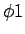 and abstracted as
and abstracted as
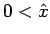 .
Also, in Principia a type is defined to be the range of
significance of a propositional function; we might write the type as
.
Also, in Principia a type is defined to be the range of
significance of a propositional function; we might write the type as
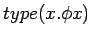 .
So the function maps this type to Prop. For example,
.
So the function maps this type to Prop. For example,
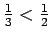 might be abstracted to
might be abstracted to
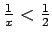 ;
it is not
meaningful for x = 0.
;
it is not
meaningful for x = 0.
In the logic presented here, propositional functions also map types T to
Prop. Given a type T we denote the category of propositional functions
over T as
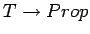 .
Instead of using 0 < x, we denote the
abstractions in the manner of Church with lambda notationlambda
notation,
.
Instead of using 0 < x, we denote the
abstractions in the manner of Church with lambda notationlambda
notation,
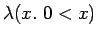 .
The details of the function notation will
not concern us until section 2.9. It suffices now to say that
given a specific proposition such as 0 < 1, we require that the individuals
such as 0, 1 be elements of types, here
.
The details of the function notation will
not concern us until section 2.9. It suffices now to say that
given a specific proposition such as 0 < 1, we require that the individuals
such as 0, 1 be elements of types, here
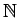 .
The function maps
.
The function maps
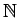 to Prop, thus an element of the category
to Prop, thus an element of the category
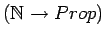 .
Given a function P in
.
Given a function P in
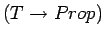 and t in the type
T, then P(t) denotes the application of P to t just as in ordinary
mathematics.
and t in the type
T, then P(t) denotes the application of P to t just as in ordinary
mathematics.



Next: Types
Up: Propositions
Previous: The category of propositions,
James Wallis
1999-09-17
![]() .
Instead of using 0 < x, we denote the
abstractions in the manner of Church with lambda notationlambda
notation,
.
Instead of using 0 < x, we denote the
abstractions in the manner of Church with lambda notationlambda
notation,
![]() .
The details of the function notation will
not concern us until section 2.9. It suffices now to say that
given a specific proposition such as 0 < 1, we require that the individuals
such as 0, 1 be elements of types, here
.
The details of the function notation will
not concern us until section 2.9. It suffices now to say that
given a specific proposition such as 0 < 1, we require that the individuals
such as 0, 1 be elements of types, here
![]() .
The function maps
.
The function maps
![]() to Prop, thus an element of the category
to Prop, thus an element of the category
![]() .
Given a function P in
.
Given a function P in
![]() and t in the type
T, then P(t) denotes the application of P to t just as in ordinary
mathematics.
and t in the type
T, then P(t) denotes the application of P to t just as in ordinary
mathematics.