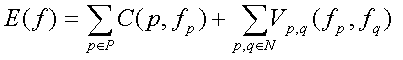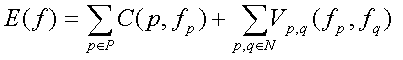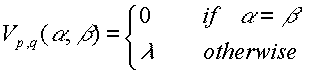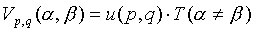Assignment 1
DUE 10/4/01, 23:59pm
This assignment is concerned with low-level
vision. Your task is to implement several different local and global
algorithms, and to performan experimental evaluation. We will give
you images with known ground truth. Note that you should do this
assignment in groups of two.
This assignment has two parts. Part
A deals with image restoration using local techniques (box filtering),
and part B deals with stereo matching
using global techniques (simulated annealing). The second part is larger
than the first one.
The test images provided will be either
in pbm format for binary images or in pgm format for grayscale images.
Your output should follow these same standards.
What to turn in: a) your
source code for all problems b) output images. c) NT executables (they
must run under NT even if you developed in another platform), d) a write-up
explaining how to run your program and a brief explanation of your
results.
Instructions
on how to turn in the assignments are here.
Part A: Image restoration - box
filtering.
1. Binary images
Write a program
that performs image restoration on a binary image using the technique of
local averaging (Box Filtering). This program should take a binary
image and window size as input and output the restored image. You
should experiment with the averaging window size and compute the accuracy
of the restoration as a function of the window size. You are free to choose
how you want to calculate accuracy as long as it is documented in your
write-up. Make good use of dynamic programming to get O(n) running time,
where n is the number of pixels. It is up to you to decide on how
to handle boundary cases. Just make sure to include in the write
up what you did.
Here is the binary image filled with
random noise that you must use:
noise_20%.pbm.
You should use the
original image with no noise in your accuracy calculation: Base.pbm
You should turn
in your restored binary image (make sure to indicate which window size
you have used). Include in your write up a graph of the restoration accuracy
as a function of window size. We are interested in hearing about
the tradeoffs between window size and the types of accuracy. So explain
your results. Do not forget to turn in your source code. Your executable
should take in a binary image and a box size and output the Box Filtering.
As an extra you might want to try your
code on this image with 40% noise: noise_40%.pbm.
This image is on the edge of being just garbage.
2. Grayscale images
This part is similar
to the previous one except that input and output are grayscale images:
Original diamond
image - diamond.pgm
As in part 1, you should turn in your
source code, executables and output image.
Part B: Stereo - simulated annealing.
This part deals with stereo matching using
global technique (simulated annealing).
Energy function - Potts model
The energy function that you should use
is
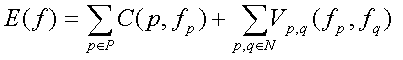
where f(p) is the disparity of pixel
p, and C(p, f(p)) is the cost of assigning pixel p disparity f(p).
This cost should be like the truncated L2 distance, which is min[(L(p)
-R(p+d))^2,K] for some constant K.
For the Potts model V is defined as
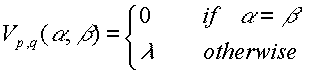
It is reasonable to use the following
modifications to the energy funcion:
Birchfield-Tomasi, which
is a data term explained in lecture, where the idea is to compute the intensity
differences using an intensity interval at each pixel.
Static clues. The static
clues are part of the smoothness term, and the idea is to decrease the
cost of a discontinuity between pixels with very different intensities.
For example in the case of the Potts model
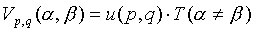
where u(p,q) = U(abs(I(p) - I(q)))
. Feel free to use a static clue that makes sense to you. One possible
choice is
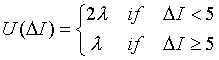
Annealing
Your annealing algorithm
should look something like this:
T = large initial value 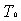
f = metropolis(E, T, f)
lower T according to some scheduling
and go to 1
metropolis(E, T, f)
disturb f in some random way
to generate f'.
dE = E(f')-E(f)
if dE<0 set f=f' Else set f = f' with probability
proportional to exp(-dE/T)
go back to one unless some condition
is meet in which case you quit.
There are many aspects of Annealing and
Metropolis which were not specified in the lectures and are not specified
here. These aspect of the implementation are up to you. For example,
you must decide what schedule you are going to use to decrease the temperature.
Also you must decide for how long will the metropolis algorithm run before
quitting. You must also choose a initial temperature. Choose
these parameters as you find best. You must include in your write-up
all your choices and why you made them. You should also plot a graph of
the energy as a function of time.
Datasets
There are two stereo
pairs for this part:
Images from the University
of Tsukuba:
The disparity range for this pair
is [-15, 0].
This pair also has a ground truth -
t.pgm
(the image is actually shifted by (18, 18) pixels). You should compare
it with your result using
accuracy measure that you think is
reasonable.
Tree sequence:
The disparity range for this pair
is [-7, 0].
The default value of regularization parameter
lambda for these images is 10.
For each pair you are given a disparity
map obtained with box filtering technique. You should use this map for
initializing the simulated annealing algorithm.