Lecture notes by Tom Roeder and Fred B. Schneider
Authorization decisions often are based on what principal is making the request and/or what principal endorses that request. So to make sense of authorization, we need to reason about propositions of the form
P says swhere P is the name of a principal and s is some statement. For example, we might model a user FBS attempting to access a file F by the formula FBS says "read F".
For the discussion that follows, anything to which a statement can be attributed is considered a principal. Thus, users, programs, services, hosts, and even wires and processors are principals. This generality affords great expressive power. For example, we might want to authorize a request "access file F" if issued by one program P1 but not if issued by another program P2, independent of which user caused those programs to execute---and making that distinction is possible when we regard P1 and P2 as distinct principals, because then P1 says access file F is not equivalent to P2 says access file F.
A statement that is encrypted by a symmetric key K can be attributed to any principal that knows K. And there will likely be multiple such principals, because symmetric keys are typically shared. A statement that is digitally signed a using private key that we call k can be attributed to the principal that knows this private key. And a statement that is encrypted using the corresponding public key, which by convention we call K, can be attributed to any principal, because public keys are assumed to be known by all. We conclude that cryptographic keys ought to be considered principals, since statements can be attributed to them.
Private keys are perhaps the most interesting among these principals, because (i) statements signed by a private key are necessarily attributed to that principal and (ii) any principal can verify whether a statement has been signed by a given private key (because such verification only requires knowledge of the corresponding public key). Recall the notation < s >k to denote a statement s digitally signed by private key k. Then we have the following inference rule for deriving a conclusion from a hypothesis,
It might seem disturbing to write "k says s" instead of "K says s" because private keys (like k) should be kept secret and public keys (like K) are not kept secret. But remember, the "k" in "k says s" is the name of the private key---not the key (value) itself.
Principals often act on behalf of other principals.
A communications channel acts on behalf of the processor that sends messages
using that channel;
a program acts on behalf of the user who initiates execution of that program;
a private key acts on behalf of the principal that causes a digital signature
to be created using that private key.
To specify such relationships among principals, we employ the notation
which is read "P speaks for Q"
and means that statements attributed to
principal P should also be
attributed to principal Q.
The meaning of
can be operationalized as an inference rule:
The concept of "speaks for" is entirely natural in the real world. Consider approaching a CS513 TA with an overdue assignment. If he says "OK, you can have an extension on your assignment", and you go home and sleep, secure in the knowledge that you have an extension. Why? You believe that the CS513 TA speaks for the CS513 professor, so you accept the statement made by the TA.
Typically, one principal is not trusted to speak for another on all matters. Although the CS513 TA speaks for the CS513 professor on some matters (like due date extensions), if the TA said "you may go to the professor's house for dinner" you would have no reason to believe you have a dinner invitation. Why? The CS513 TA probably does not speak for the professor on all matters, and it is unlikely that a TA would speak for a professor on matters of dinner invitations. (An invitation issued by the professor's spouse would be a different matter.)
To capture limitations on when one principal may act on behalf of another,
we extend our "speaks for" notation and write
to mean "P speaks for
Q only for statements in set S".
This gives rise to another inference rule (the so-called "hand-off rule"), which says
that every principal P is an
authority on which other principals can speak for P.
We should also modify the our earlier inference rule that allows
Q says s to be derived---such deductions should require
s to be an element of S when given a hypothesis
.
We wish to formalize the operation of a simple certification authority CA. Given what we know about how CA is likely to work, we would then have the following axioms:
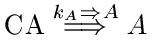
Note that we have not considered revocation; there is no way for a principal to change the key that is stored by the CA.
We now want to derive 
, which establishes
that the CA does what is expected---it allows principals to learn that a private
key kA speaks for some given principal A and therefore
the public key for A is KA.
We do this derivation by using the inference rules given above, starting
with the 3 axioms formalizing the information stored by the CA.
A hierarchical name is a name constructed as a sequence of simple names. Each simple name in a hierarchical name is relative to the prefix that precedes it. So, for example, the hierarchical name / A / B / C / D / E involves simple names A, B, C, D, and E . Simple name B is relative to / A; simple name C is relative to / A / B ; and so on.
One virtue of having a hierarchical name space is that local uniqueness tests can be used to ensure global uniqueness of a name. Add a (locally) unique simple name to a hierarchical name and the result is a unique new hierarchical name.
When names are hierarchical, a natural way to implement a CA is by using a tree of hosts, each of which stores one or more certificates. The root host partitions the name space and delegates a unique partition to each of its successors. In particular, the root delegates to a successor named A the responsibility for names of the form / A / ... and delegates to a success B the responsibility for names of the form / B / ... , and so on. Each of these first-level hosts, in turn, delegates to its successors according to the next simple name in a hierarchical name. The result is depicted by the following figure, where to the right of each node is a certificate that host manages. Notice, each certificate is signed using the private key associated with the predecessor in the tree.
Each level of the CA stores a certificate that can be used to validate certificates stored in the next level down. In particular, each host stores a certificate for the public key that is used to validate certificates stored in the direct descendants of that host.
To establish that this suffices, we need only show that
can be derived from a formalization of this architecture.
So, as before, we write down some "axioms" that describe what
is the meaning of the information stored by CA hosts.
First, we have an axiom that formalizes our intention that a given CA host is an authority on hierarchical names that extend its prefix, so this host speaks for all CA's below it in the tree. We can formalize this statement as
Given a root key Ke (= public key for ke, where e is the empty path), we have the following certificates that we will use in our proof. Each of these certificates will exist at some node of the above tree:
This then gives us the following proof:
