Homework 4

CS 482 - Spring 2005

Due: Friday, Mar 4

Note: Include your Cornell NetID on your each section of your homework. This simplifies the process of recording your grades.

Part A

1. Problem 2 at the end of Chapter 7. The figures referred to in the problem are Figures 7.23 and 7.24  This is the problem that starts, "In the figure below is a flow network,...".  Full text now appears below.

   In the figure below is a flow network, on which an s-t flow has been computed. The capacity of each edge appears as a label next to the edge, and the numbers in boxes give the amount of flow sent on each edge. (Edges without boxed numbers --- specifically the four edges of capacity 3 --- have no flow being sent on them.)

   1. What is the value of this flow? Is this a maximum s-t flow in this graph?
   2. Find a minimum s-t cut in the above flow network, and also say what its capacity is. (The capacity of each individual edge appears as a label next to the edge.)

Part B

2. Problem 6 at the end of Chapter 7. This is the problem that starts, "Suppose you're a consultant for the Ergonomic Architecture Commission, and they...".  Full text now appears below.

   Suppose you're a consultant for the Ergonomic Architecture Commission, and they come to you with the following problem.

   They're really concerned about designing houses that are "user-friendly," and they've been having a lot of trouble with the set-up of light fixtures and switches in newly designed houses. Consider, for example, a one-floor house with n light fixtures and n locations for light switches mounted in the wall. You'd like to be able to wire up one switch to control each light fixture, in such a way that a person at the switch can see the light fixture being controlled.

   Sometimes this is possible, and sometimes it isn't. Consider the two simple floor plans for houses in the accompanying figure. There are three light fixtures (labeled a, b, c) and three switches (labeled 1, 2, 3). It is possible to wire switches to fixtures in the example on the left so that every switch has line-of-sight to the fixture, but this is not possible in the example on the right.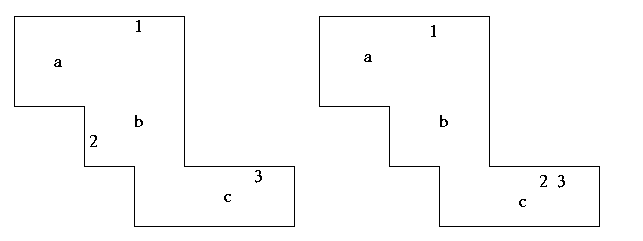

   Let's call a floor plan --- together with n light fixture locations and n switch locations --- "ergonomic" if it's possible to wire one switch to each fixture so that every fixture is visible from the switch that controls it. A floor plan will be represented by a set of m horizontal or vertical line segments in the plane (the walls), where the i^th wall has endpoints (x_i,y_i), (x_i', y_i'). Each of the n switches and each of the n fixtures is given by its coordinates in the plane. A fixture is visible from a switch if the line segment joining them does not cross any of the walls.

   Give an algorithm to decide if a given floor plan, in the above representation, is ergonomic. The running time should be polynomial in m and n. You may assume that you have a subroutine with O(1) running time that takes two line segments as input and decides whether or not they cross in the plane.

Part C

3. Problem 7 at the end of Chapter 7. This is the problem that starts, "Consider a set of mobile computing clients in a certain town...".  Full text now appears below.

   Consider a set of mobile computing clients in a certain town who each need to be connected to one of several possible base stations. We'll suppose there are n clients, with the position of each client specified by its (x,y) coordinates in the plane. There are also k base stations; the position of each of these is specified by (x,y) coordinates as well.

   For each client, we wish to connect it to exactly one of the base stations. Our choice of connections is constrained in the following ways. There is a range parameter r --- a client can only be connected to a base station that is within distance r. There is also a load parameter L --- no more than L clients can be connected to any single base station.

   Your goal is to design a polynomial-time algorithm for the following problem. Given the positions of a set of clients and a set of base stations, as well as the range and load parameters, decide whether every client can be connected simultaneously to a base station, subject to the range and load conditions in the previous paragraph.