
Fig: Partitioning the feature space.
In other words: if the distance to the partition is larger than the distance to our closest neighbor, we know that none of the data points inside that partition can be closer.
Fig: Partitioning the feature space.

Fig 2: The bounding of the distance between \(\vec x_t\) and \(\vec x\) with KD-trees and Ball trees (here \(\vec x\) is drawn twice, once for each setting). The distance can be dissected into two components \(d(\vec x_t,\vec x)=d_1+d_2\), where \(d_1\) is the outside ball/box component and \(d_2\) the component inside the ball/box. In both cases \(d_1\) can be lower bounded by the distance to the wall, \(d_w\), or ball, \(d_b\), respectively i.e. \(d(\vec x_t,\vec x)=d_1+d_2\geq d_w+d_2\geq d_w\).
Tree Construction:
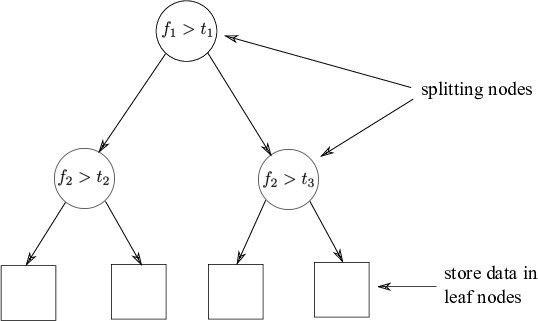
Fig: The partitioned feature space with corresponding KD-tree.
Which partitions can be pruned?
Note: Steps 3 & 4 pick the direction with a large spread (\(x_{1} - x_{2}\))