Lecture 3: The Perceptron

Binary classification (i.e. $y_i \in \{-1, +1\}$)
Data is linearly separable

Classifier

$$ h(x_i) = \textrm{sign}(\vec{w} \cdot \vec{x_i} + b) $$

$b$ is the bias term (without the bias term, the hyperplane that $\vec{w}$ defines would always have to go through the origin). Dealing with $b$ can be a pain, so we 'absorb' it into the feature vector $\vec{w}$ by adding one additional constant dimension. Under this convention, $$ \vec{x_i} \hspace{0.1in} \text{becomes} \hspace{0.1in} \begin{bmatrix} \vec{x_i} \\ 1 \end{bmatrix} \\ \vec{w} \hspace{0.1in} \text{becomes} \hspace{0.1in} \begin{bmatrix} \vec{w} \\ b \end{bmatrix} \\ $$ We can verify that $$ \begin{bmatrix} \vec{x_i} \\ 1 \end{bmatrix} \cdot \begin{bmatrix} \vec{w} \\ b \end{bmatrix} = \vec{w} \cdot \vec{x_i} + b $$ Using this, we can simplify the above formulation of $h(x_i)$ to $$ h(x_i) = \textrm{sign}(\vec{w} \cdot \vec{x}) $$

(Left:) The original data is 1-dimensional (top row) or 2-dimensional (bottom row). There is no hyper-plane that passes through the origin and separates the red and blue points. (Right:) After a constant dimension was added to all data points such a hyperplane exists.

Observation: Note that $$ y_i(\vec{w} \cdot \vec{x_i}) > 0 \Longleftrightarrow x_i \hspace{0.1in} \text{is classified correctly} $$ where 'classified correctly' means that $x_i$ is on the correct side of the hyperplane defined by $\vec{w}$. Also, note that the left side depends on $y_i \in \{-1, +1\}$ (it wouldn't work if, for example $y_i \in \{0, +1\}$).

Perceptron Algorithm

Now that we know what the $\vec{w}$ is supposed to do (defining a hyperplane the separates the data), let's look at how we can get such $\vec{w}$.

Perceptron Algorithm

Geometric Intuition

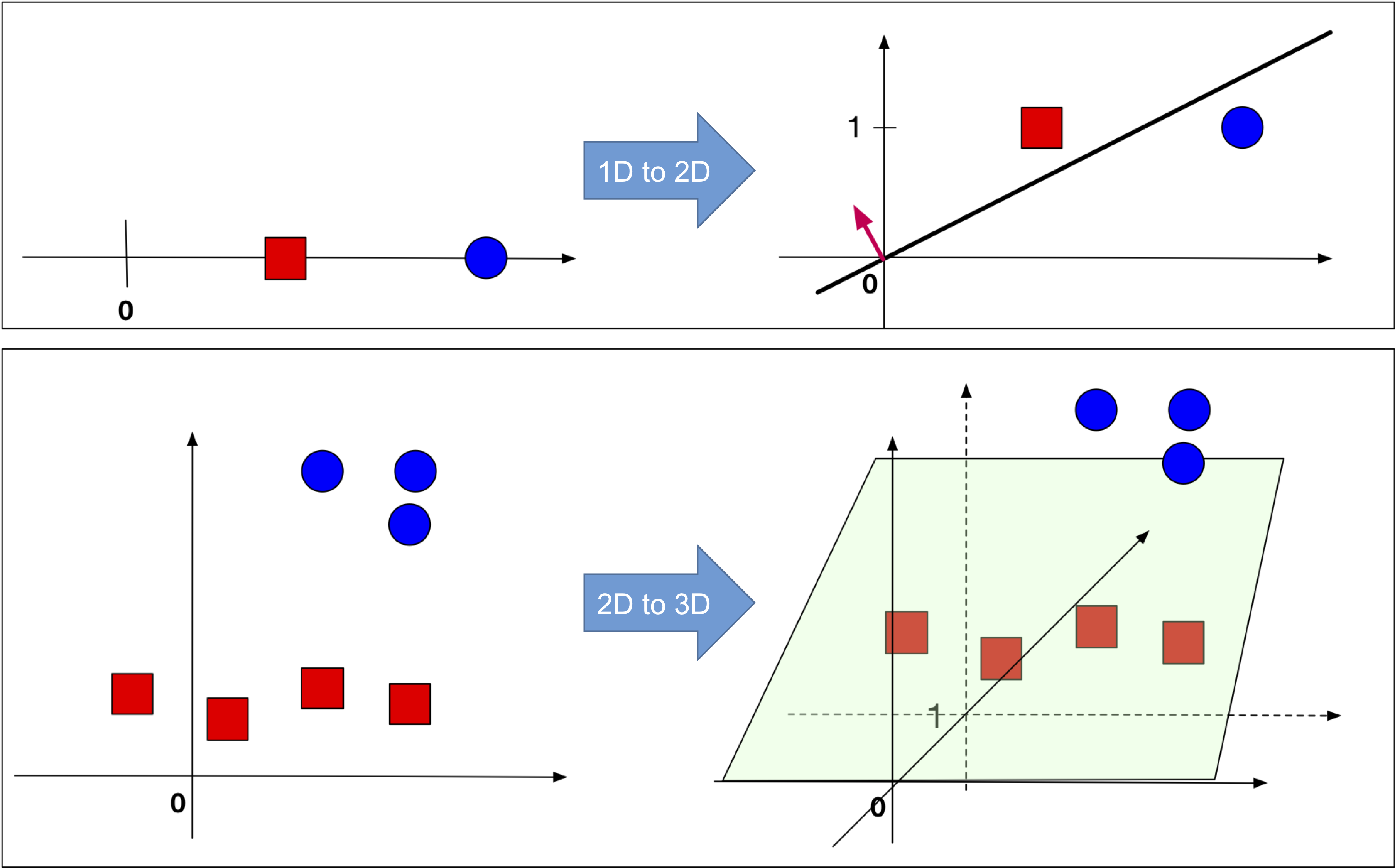
Illustration of a Perceptron update. (Left:) The hyperplane defined by $\mathbf{w}_t$ misclassifies one red (-1) and one blue (+1) point. (Middle:) The red point $\mathbf{x}$ is chosen and used for an update. Because its label is -1 we need to subtract $\mathbf{x}$ from $\mathbf{w}_t$. (Right:) The udpated hyperplane $\mathbf{w}_{t+1}=\mathbf{w}_t-\mathbf{x}$ separates the two classes and the Perceptron algorithm has converged.

Quiz: How often can a Perceptron misclassify a point $\mathbf{x}$ repeatedly?

Perceptron Convergence

Suppose that $\exists \vec{w}^*$ such that $y_i(\vec{w}^* \cdot \vec{x}) > 0 $ $\forall (\vec{x}_i, y_i) \in D$.

Now, suppose that we rescale each data point and the $\vec{w}^*$ such that $$ ||\vec{w}^*|| = 1 \hspace{0.3in} \text{and} \hspace{0.3in} ||\vec{x_i}|| \le 1 \hspace{0.1in} \forall \vec{x_i} \in D $$ The Margin of a hyperplane, $\gamma$, is defined as $$ \gamma = \min_{(\vec{x_i}, y_i) \in D}|\vec{w}^* \cdot \vec{x_i} | $$ We can visualize this as follows

All inputs $\vec{x_i}$ live within the unit sphere
$\gamma$ is the distance from the hyperplane (blue) to the closest data point
$\vec{w}^*$ lies on the unit sphere

Theorem: If all of the above holds, then the perceptron algorithm makes at most $1 / \gamma^2$ mistakes.

Proof:
Keeping what we defined above, consider the effect of an update ($\vec{w}$ becomes $\vec{w}+y\vec{x}$) on the two terms $\vec{w} \cdot \vec{w}^*$ and $\vec{w} \cdot \vec{w}$. We will use two facts:

$y( \vec{x}\cdot \vec{w})\leq 0$: This holds because $\vec x$ is misclassified by $\vec{w}$ - otherwise we wouldn't make the update.
$y( \vec{x}\cdot \vec{w}^*)>0$: This holds because $\vec{w}^*$ is a separating hyper-plane and classifies all points correctly.

Consider the effect of an update on $\vec{w} \cdot \vec{w}^*$: $$ (\vec{w} + y\vec{x}) \cdot \vec{w}^* = \vec{w} \cdot \vec{w}^* + y(\vec{x}\cdot \vec{w}^*) \ge \vec{w} \cdot \vec{w}^* + \gamma $$ The inequality follows from the fact that, for $\vec{w}^*$, the distance from the hyperplane defined by $\vec{w}^*$ to $\vec{x}$ must be at least $\gamma$ (i.e. $y (\vec{x}\cdot \vec{w}^*)=|\vec{x}\cdot\vec{w}^*|\geq \gamma$).

This means that for each update, $\vec{w} \cdot \vec{w}^*$ grows by at least $\gamma$.
Consider the effect of an update on $\vec{w} \cdot \vec{w}$: $$ (\vec{w} + y\vec{x})\cdot (\vec{w} + y\vec{x}) = \vec{w} \cdot \vec{w} + 2y(\vec{w} \cdot\vec{x}) + y^2(\vec{x}\cdot \vec{x}) \le \vec{w} \cdot \vec{w} + 1 $$ The inequality follows from the fact that
- $2y(\vec{w}\cdot \vec{x}) < 0$ as we had to make an update, meaning $\vec{x}$ was misclassified
- $y^2(\vec{x} \cdot \vec{x}) \le 1$ as $y^2 = 1$ and all $\vec{x}\cdot \vec{x}\leq 1$ (because $\|\vec x\|\leq 1$).

This means that for each update,

grows by at most 1

Now we can put together the above findings. Suppose we had $M$ updates. \begin{align} M\gamma &\le \vec{w}\cdot\vec{w}^* &&\text{By (1)} \\ &= |\vec{w}\cdot\vec{w}^*| &&\text{By (1) again (the dot-product must be non-negative because the initialization is 0 and each update increases it by at least $\gamma$)} \\ &\le ||\vec{w}||\ ||\vec{w}^*|| &&\text{By Cauchy-Schwartz inequality} \\ &= ||\vec{w}|| &&\text{As $||\vec{w}^*|| = 1$} \\ &= \sqrt{\vec{w} \cdot \vec{w}} && \text{by definition of $\|\vec{w}\|$} \\ &\le \sqrt{M} &&\text{By (2)} \\ &\Rightarrow M\gamma \le \sqrt{M} \\ &\Rightarrow M^2\gamma^2 \le M \\ &\Rightarrow M \le \frac{1}{\gamma^2} \end{align}

History

Initially, huge wave of excitement ("Digital brains")
Then, contributed to the A.I. Winter. Famous counter-example XOR problem (Minsky 1969):

If data is not linearly separable, it loops forver.