16: KD Trees

Processing math: 100%

16: KD Trees

Time Complexity of k-NN

Let's look at the time complexity of k-NN.
We are in a

$d$ -dimensional space.
To make it easier, let's assume we've already processed some number of inputs, and we want to know the time complexity of adding one more data point.
When training, k-NN simply memorizes the labels of each data point it sees.
This means adding one more data point is

$O(d)$ .
When testing, we need to compute the distance between our new data point and all of the data points we trained on.
If

$n$ is the number of data points we have trained on, then our time complexity for training is

$O(dn)$ .
Classifying one test input is also

$O(dn)$ .
To achieve the best accuracy we can, we would like our training data set to be very large (

$n\gg 0$ ), but this will soon become a serious bottleneck during test time.
Goal: Can we make k-NN faster during testing? We can if we use clever data structures.

k-Dimensional Trees

The general idea of KD-trees is to partition the feature space.
We want discard lots of data points immediately because their partition is further away than our

$k$ closest neighbors.
We partition the following way:

Divide your data into two halves, e.g. left and right, along one feature.
For each training input, remember the half it lies in.

How can this partitioning speed up testing?
Let's think about it for the one neighbor case.

Identify which side the test point lies in, e.g. the right side.
Find the nearest neighbor $x^R_{\mathrm{NN}}$ of $x_t$ in the same side. The $R$ denotes that our nearest neighbor is also on the right side.
Compute the distance between $x_y$ and the dividing "wall". Denote this as $d_w$ . If $d_w > d(x_t, x^R_{\mathrm{NN}})$ you are done, and we get a 2x speedup.

Fig: Partitioning the feature space.

In other words: if the distance to the partition is larger than the distance to our closest neighbor, we know that none of the data points inside that partition can be closer.
We can avoid computing the distance to any of the points in that entire partition.
We can prove this formally with the triangular inequality. (See Figure 2 for an illustration.)
Let

$d(x_t,x)$ denote the distance between our test point

$x_t$ and a candidate

$x$ . We know that

$x$ lies on the other side of the wall, so this distance is dissected into two parts

$d(x_t,x)=d_1+d_2$ , where

$d_1$ is the part of the distance on

$x_t's$ side of the wall and

$d_2$ is the part of the distance on

$x's$ side of the wall. Also let

$d_w$ denote the shortest distance from

$x_t$ to the wall. We know that

$d_1>d_w$ and therefore it follows that

$d(x_t, x)=d_1+d_2\geq d_w+d_2 \geq d_w.$ This implies that if

$d_w$ is already larger than the distance to the current best candidate point for the nearest neighbor, we can safely discard

$x$ as a candidate.

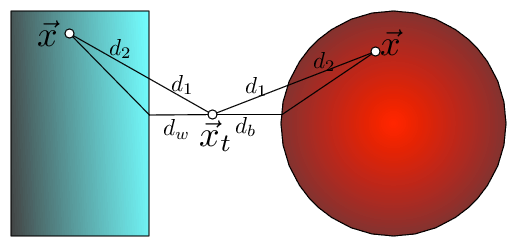
Fig 2: The bounding of the distance between $\vec x_t$ and $\vec x$ with KD-trees and Ball trees (here $\vec x$ is drawn twice, once for each setting). The distance can be dissected into two components $d(\vec x_t,\vec x)=d_1+d_2$ , where $d_1$ is the outside ball/box component and $d_2$ the component inside the ball/box. In both cases $d_1$ can be lower bounded by the distance to the wall, $d_w$ , or ball, $d_b$ , respectively i.e. $d(\vec x_t,\vec x)=d_1+d_2\geq d_w+d_2\geq d_w$ .

Quiz: Construct a case where this does not work.

KD-tree data structure

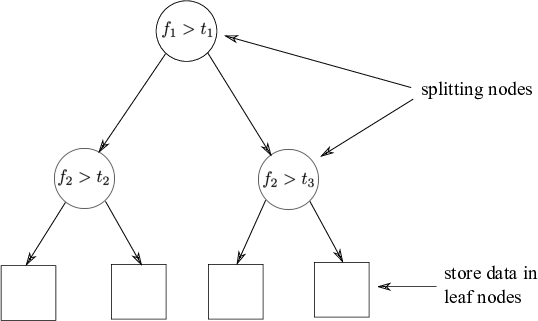
Fig: The partitioned feature space with corresponding KD-tree.

Tree Construction:

Split data recursively in half on exactly one feature.
Rotate through features.

When rotating through features, a good heuristic is to pick the feature with maximum variance.

Example:

Which partitions can be pruned?
Which must be searched and in what order?
Pros:

Exact.
Easy to build.

Cons:

Curse of Dimensionality makes KD-Trees ineffective for higher number of dimensions.
All splits are axis aligned.

Approximation: Limit search to

$m$ leafs only.

Ball-trees

Similar to KD-trees, but instead of boxes use hyper-spheres (balls). (See Figure 2 for an illustration.)
As before we can dissect the distance and use the triangular inequality

$\begin{equation} d(x_{t}, x)=d_1+d_2\geq d_{b} + d_2\geq d_b\label{eq:balldist} \end{equation}$ If the distance to the ball,

$d_b$ , is larger than distance to the currently closest neighbor, we can safely ignore the ball and all points within.
The ball structure allows us to partition the data along an underlying manifold that our points are on, instead of repeatedly dissecting the entire feature space (as in KD-Trees).

Ball-tree Construction

Input: set

$S$ ,

$n=\vert S \vert$ ,

$k$

Note: Steps 3 & 4 pick the direction with a large spread (

$x_{1} - x_{2}$ )

Ball-Tree Use

Same as KD-Trees
Slower than KD-Trees in low dimensions (

$d \leq 3$ ) but a lot faster in high dimensions. Both are affected by the curse of dimensionality, but Ball-trees tend to still work if data exhibits local structure (e.g. lies on a low-dimensional manifold).

Summary

$k$ -NN is slow during testing because it does a lot of unecessary work.
KD-trees partition the feature space so we can rule out whole partitions that are further away than our closest $k$ neighbors. However, the splits are axis aligned which does not extend well to higher dimensions.
Ball-trees partition the manifold the points are on, as opposed to the whole space. This allows it to perform much better in higher dimensions.