CS4620 Introduction to Computer Graphics
CS4621 Computer Graphics Practicum
Cornell University
MWF 2:30pm, Hollister B14
F 3:35pm, Kimball B11 [4621 only]
Instructor: Kavita Bala
Staff
Graduate TAs
Eston Schweickart (CS4620 head TA, ers@cs.cornell.edu)
Nicolas Savva (CS4621 head TA, nsavva@graphics.cornell.edu)
Brandon Benton (bnb32@cornell.edu)
Bryce Evans (bae43@cornell.edu)
Fujun Luan (fl356@cornell.edu)
Eric Gao (emg222@cornell.edu)
Zeqiang Zhao (zz432@cornell.edu)
Ugrad TAs
Jimmy Briggs (jeb482@cornell.edu)
Kristen Crasto (kmc376@cornell.edu)
Kyle Genova (kag278@cornell.edu)
Tongcheng Li (tl486@cornell.edu)
Andrew Mullen (asm278@cornell.edu)
Katherine Salesin (kas493@cornell.edu)
Ning Wang (nw265@cornell.edu)
Kelly Yu (kly24@cornell.edu)
Cristian Zaloj (cz68@cornell.edu)
Schedule
| date | topic | reading | assignments | |
|---|---|---|---|---|
| 26 | Aug | Introduction slides | Ch. 1, Ch. 2 | |
| 28 | Aug | Triangle meshes slides | Ch. 12, up to 12.1.4 | PA1: Meshes out |
| 31 | Aug | Triangle meshes slides | ||
| 2 | Sep | Blender Mesh Tutorial slides | ||
| 4 | Sep | History of Computer Graphics | ||
| 7 | Sep | —Labor Day— | ||
| 9 | Sep | Ray tracing intersection slides | Ch. 4, up to 4.4 | |
| 11 | Sep | Ray tracing intersection 2 slides | PA1: Meshes due 9/10, PA2: Ray1 out | |
| 14 | Sep | Ray tracing shading slides | Ch. 4.5 onward | |
| 16 | Sep | Pipeline and 2D transformations slides | Ch. 5, Sec. 6.1 | |
| 18 | Sep | 2D transformations slides | ||
| 21 | Sep | Hierarchies and Scene Graphs slides | Sec 12.2 | |
| 23 | Sep | 3D transformations slides | Ch. 6: 6.2 to end | |
| 25 | Sep | Perspective slides | PA2: Ray1 due, PA3: Scenes out | |
| 28 | Sep | Viewing: Orthographic slides | Ch. 7 | |
| 30 | Sep | Open GL slides | ||
| 2 | Oct | Viewing: Perspective (viewExplorer) slides | ||
| 5 | Oct | Rasterization slides | Ch 8 up to 8.1 | |
| 7 | Oct | Graphics Pipeline slides | notes on perspective correct textures | Ch 8: 8.2 to end | |
| 9 | Oct | GLSL slides | PA3: Scenes due | |
| 12 | Oct | —Fall Break— | ||
| 14 | Oct | Textures 1 slides | PA4: Shaders out | |
| 16 | Oct | Textures 2 slides | ||
| 19 | Oct | Textures 3 slides | ||
| 21 | Oct | Textures 4 slides | ||
| 23 | Oct | Antialiasing and compositing slides | Ch 3: up to 3.4 | |
| 26 | Oct | GPUs slides | ||
| 28 | Oct | GPUs and Splines 1 slides | ||
| 30 | Oct | Splines 2 slides | Ch. 15: up to 15.5 | PA4: Shaders due 10/29 |
| 2 | Nov | Splines 3 slides | Ch. 15: up to 15.6.2 | PA5: Splines out |
| 4 | Nov | Splines 4 slides | ||
| 6 | Nov | Splines 5 slides | ||
| 9 | Nov | Surfaces 1 slides | ||
| 11 | Nov | Surfaces 2 and Animation 1 slides | ||
| 13 | Nov | Animation 2 slides | PA5: Splines due, PA6: Animation out | |
| 16 | Nov | Animation 3 slides | ||
| 18 | Nov | Ray Tracing acceleration slides | ||
| 20 | Nov | Reflection and illumination slides | PA6: Animation due, PA7: Ray2 out | |
| 23 | Nov | Reflection slides | ||
| 25 | Nov | —Thanksgiving— | ||
| 27 | Nov | —Thanksgiving— | ||
| 30 | Nov | Advanced ray tracing and Images slides | ||
| 2 | Dec | Images slides | ||
| 4 | Dec | Conclusions slides | PA7: Ray2 due 12/3 | |
Projects
There will be 7 projects during the semester, due approximately every two weeks.
PA 1: Meshes
Due: Thursday 10th September 2015 (11:59pm)
Do this project alone or in groups of two, as you prefer. You can use Piazza to help pair yourselves up.
Introduction
In this assignment you will learn about the most widely used way to represent surfaces for graphics: triangle meshes. A triangle mesh is basically just a collection of triangles in 3D, but the key thing that makes it a mesh rather than just a bag of triangles is that the triangles are connected to one another to form a seamless surface. The textbook and lecture slides discuss the data structures used for storing and manipulating triangle meshes, and in this assignment we will work with the simplest kind of structure: a shared-vertex triangle mesh, also known as an indexed triangle mesh.
Your job in this assignment is to write a simple mesh generation and processing utility that is capable of building triangle meshes to approximate some simple curved surfaces, and also can add some information to existing meshes. It reads and writes meshes stored in the popular OBJ file format, a text format with one line for each vertex and face in the mesh.
Building a pyramid
The written part of this assignment is a warmup for generating more complex meshes. Suppose we wish to generate a mesh (with just vertex positions, no normals or texture coordinates) for a square pyramid (like the one at Giza). The base is a square in the x-z plane, going from -1 to 1 on each axis and the apex is at (0,1,0). Let us now add a triangular flag to our pyramid. We would like the base of the flag to be at the apex of the pyramid and the top to reach a height of 1.5 vertically above. Orient the flag in the positive x-z direction and make it stretch out, 0.5 units away from the center, terminating at the same height as the base. Write out:
- The coordinates of the 7 vertices;
- The indices of the 7 triangles (you will need two for the base).
The answer consists of 21 floating point numbers (3D coordinates of the vertices) and 21 integers (indices into the list of vertices, 3 for each triangle).
To test out your solution, type it into a text file with the vertices, one per line, and then the triangles, also one per line. Precede each vertex with "v" and each triangle with "f". Note that the indices for the vertices, making up a particular triangle face, should be listed in a counter-clockwise order as viewed from the outside of the given mesh. And one more thing: add one to all the vertex indices, so that the count starting from 1. (Caution! this is not the same as what we do in the data structures inside the program!) For example, a single triangle in the x-z plane, facing towards +y is:
v 0 0 0 v 0 0 1 v 1 0 0 f 1 2 3
This text file is now an OBJ file!
Once you are done making the necessary modifications the final mesh should be the same as the one in the following figure.

Read the completed file into one of the mesh viewers described below, take a couple of screen shots to show that it works, and include them with your writeup.
The OBJ files written by the framework are a little more complicated because they can contain additional data at the vertices: normals and texture coordinates.
Specification
The utility "meshgen" is a mesh-generation program that runs at the command line. Its usage is:
meshgen [-n] [-m] [-r] sphere|cylinder|torus|cube -o <outfile>.obj meshgen [-nv] -f <infile>.obj -o <outfile>.obj
The first required argument is the mesh specifier, and the second is the output filename. If the mesh specifier is one of the fixed strings "sphere", "cylinder", "cube", or "torus", a triangle mesh is generated that approximates that shape, where the number of triangles generated is controlled by the optional -n and -m options (details below), and written to the output file.
A triangle mesh that is an approximation of a smooth surface should have normal vectors stored at the vertices that indicate the direction normal to the exact surface at that point. When generating the predefined shapes, you generate points that are on the surface, and for each you should also calculate the normal vector that is perpendicular to the surface at that point.
If the mesh specifier is -f followed by the name of an OBJ file, the mesh in that file is read. If the -nv flag is given, any vertex normals are discarded and new vertex normals appropriate for a smooth surface are computed from the triangle geometry as described below. Finally, the mesh is writen to the output file.
Details of predefined shapes
Cylinder
The cylinder has radius 1 and height 2 and is centered at the origin; its axis is aligned with the y axis. It is tesselated with n divisions around the outer surface. The two ends of the cylinder are closed by disc-shaped caps. The vertices around the rims of the cylinder are duplicated to allow discontinuities in the normals and texture coordinates. Each cap consists of one set of the duplicated vertices around the appropriate rim as well as a single point where the cap meets the y axis. This point is incorporated into each triangle in the cap.
Texture coordinates on the outer surface are like the sphere in u, running from 0 to 1 in a counterclockwise direction as viewed from the +y direction, and run from 0 to 0.5 in v, increasing in the +y direction. The texture coordinates for the two caps are circles inscribed in the upper-left (for the -y cap) and upper-right (for the +y cap) quadrants of the unit square, with the +u direction corresponding to the +x direction in 3D space, and the v direction arranged to keep the texture right-reading. We have provided a partial implementation of the cylinder.
Sphere
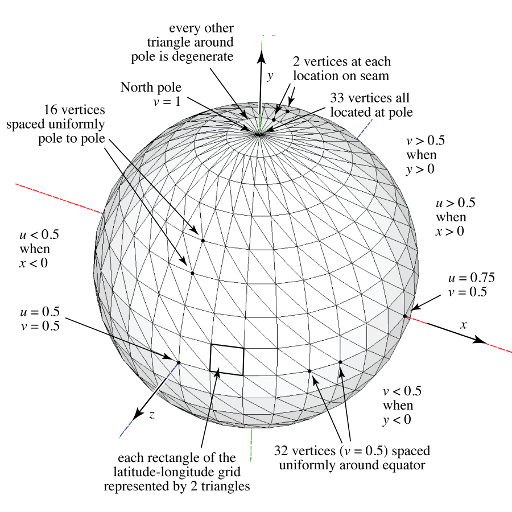
The sphere has radius 1 and is centered at the origin in 3D coordinates. It is tesselated in latitude-longitude fashion, with n divisions around the equator and m divisions from pole to pole along each line of longitude. The North pole is at (0,1,0), the South pole at (0,-1,0), and points on the Greenwich meridian have coordinates (0,y,z) with (z > 0). The mesh is generated with vertex normals that are normal to the exact sphere, and with texture coordinates (u,v) where u depends only on longitude, with (u=0) at longitude 180 degree West and u=1 at 180 degrees East, and v depends only on latitude, with (v=0) at the South Pole and (v=1) at the North pole. Each quadrilateral formed by two adjacent longitude lines and two adjacent latitude lines is divided on the diagonal to form two triangles. The vertices along the 180th meridian are duplicated: one vertex has texture coordinate (u=0) and the other has texture coordinate (u=1), to enable correct wrapping of a tileable texture image across the seam. The vertices at the poles are duplicated (n+1) times, to enable nearly-appropriate texture in the row of triangles adjacent to the pole. You may have noticed that the triangles get compressed near the poles. An alternative tesselation approach can be used to create an isotropic mesh (See icosphere for more details. The implementation is left as an extra credit exercise for those who wish to explore this further).

Torus
A torus is a doughnut-shaped surface defined by a major radius, affecting the size of the hole, and a minor radius, affecting the thickness of the ring. Your code should create a torus with major radius 1 and minor radius r (controlled by the -r flag with a default of 0.25). Its u coordinates are like the sphere, and the v coordinate runs from 0 to 1 with a seam on the inside of the torus, with the direction arranged so that the texture is right-reading from the outside. Like the sphere it has a seam on the -z half of the y-z plane, and it has a similar seam around the inside of the tube; vertices along each seam are duplicated twofold and a single vertex, at the position (0, 0, -1+r), is duplicated fourfold.

Computing vertex normals
For a mesh that has vertex positions and triangles, but no vertex normals, one often wants to compute vertex normals so that the mesh can appear smooth. But since the original surface, if there even was one, is forgotten, we need some way to make up plausible normals. There are a number of ways to do this, and we'll use a simple one for this assignment: the normal at a vertex is the average of the geometric normals of the triangles that share this vertex.
Your first thought might be to do this as a loop over vertices, with an inner loop over the triangles that share that vertex:
for each vertex v
normal[v] = (0,0,0)
for each triangle t around v
normal[v] += normal of triangle t
normal[v].normalize()
With the appropriate data structures, this is possible, but in our case there's no efficient way to do the inner loop: our data structure tells us what vertices belong to a triangle, but the only way to find triangles that belong to a vertex is to search through the whole list of triangles. This is possible but would be quadratic in the mesh size, which is bad news for large meshes.
However, it's simple to do it with the loops interchanged:
for each vertex v
normal[v] = (0,0,0)
for each triangle t
for each vertex v around t
normal[v] += normal of triangle t
for each vertex v
normal[v].normalize()
This way the inner loop can efficiently visit just the necessary vertices. Nifty!
You should compute normals whenever the -nv flag is turned on; the logic to do this is already in the framework.
Framework
The framework is available on a public Git repository: https://github.com/CornellCS4620/Framework.git
If you have not used Git before, you can follow the tutorial here, or ask a TA for assistance. Once you have the code set up on your local machine, we recommend that you create a new branch (named, for example, my-solution), and commit all changes you make to that branch. When releasing future assignments, we will ask you to pull from our updated repository onto your master branch; creating your own solution branch will avoid the headaches of merge conflicts. We encourage you to use version control though we request that you refrain from publicly sharing your class repository.
Setting Up Your Workspace For Eclipse
- After grabbing the repo and creating your own branch, you may fire up Eclipse to get started with coding.
- Navigate to and press "File->Import"
- Choose the option "General->Existing Projects Into Workspace"
- Press "Next"
- For the root directory, browse and select the folder CS4620, which may be found directly in the repo's root folder.
- Press "Finish".
You have set up a coding environment, but you're not done yet. Right-click on the CS4620 project in Package Explorer and press "Build Path->Configure Build Path"Navigate to the "Libraries" tabExpand the lwjgl.jar file and select "Native library location"Press "Edit" and enter in your specific path, which will be "CS4620/deps/native/<OS>".
We have marked all the functions or parts of the functions you need to complete in with TODO#A1 in the source code. To see all these TODO#A1 annotations in Eclipse, select Search menu, then File Search and type TODO#A1 TODO's in Eclipse can be viewed through the Task List as well. You should only need to modify those the sections marked with TODO unless you want to add other cool mesh generators for extra credit (in which case look at cs4620.util.MeshGen's switch block). All other functionality has been implemented.
The following video contains a walkthrough for setting up your repository, importing into Eclipse, running your code, and viewing the results. The tutorial assumes that you have already installed a git command-line tool as well as the Eclipse IDE.
Testing your program
- The entry point of this assignment is cs4620.util.MeshGen
- Select that Java class in the Package Explorer and press the play button.
- Unless you have already put in arguments to the program, you should get an output that no arguments have been provided
- Navigate to and press "Run->Run Configurations..."
- Pick Java Application
- Select the tab "Arguments"
- Type in your arguments into "Program arguments": (eg. "cube -o cube.obj")
- Run it
Since your program just writes a file full of inscrutable numbers, you need some way to look at the results. For this you can use MeshLab. Please refer to the notes from lecture on Sept 3rd for more information about how to get MeshLab and how to use it to load an OBJ mesh and find out what it contains. (Here are a few more programs that might be worth checking out: Blender, ObjViewer, p3d.in ). Warning: Blender discards the normals stored in the OBJ file and as such is not a good tool to check whether your normals are correct. Caution: Blender by default will rotate your mesh by 90 degrees around the x axis so that it displays right way up in Blender's z-is-up world.
Download and unpack the following archive: MeshesTestData.zip

Handing in
Submit a zip file containing your solution using CMS
You should include a readme in your zip that contains:
- You and your partner's names and NetIDs.
- Anything else you want us to know.
Separately submit a zip file containing your paper and pencil on CMS. The solution for the paper and pencil parts of the homework will be done alone, and not in pairs. Please turn that in separately at the appropriate place in CMS.
PA 2 Code: Ray Tracing 1
Due: Thursday 24 September 2015 (11:59pm)
Do this project alone or in groups of two, as you prefer. You can use Piazza to help pair yourselves up.
Do the written part alone.
Introduction
Ray tracing is a simple and powerful algorithm for rendering images. Within the accuracy of the scene and shading models and with enough computing time, the images produced by a ray tracer can be physically accurate and can appear indistinguishable from real images. Cornell pioneered research in accurate rendering. See http://www.graphics.cornell.edu/online/box/compare.html for the famous Cornell box, which exists in Rhodes Hall.
The basic idea behind ray tracing is to model the movement of photons as they travel along their path from a light source, to a surface, and finally to a viewer's eye. Tracing forward along this path is difficult, since it can be unclear which photons will make it to the eye, especially when photons can bounce between objects several times along their path (and in unpredictable ways). To simplify the system, these paths are computed in reverse; that is, rays originate from the position of the eye. Color information, which depends on the scene's light sources, is computed when these rays intersect an object, and is sent back towards the eye to determine the color of any particular pixel.
In this assignment, you will complete an implementation of a ray tracer. It will not be able to produce physically accurate images, but later in the semester you will extend it to produce nice looking images with many interesting effects.
We have provided framework code to save you from spending time on class hierarchy design and input/output code, and rather to have you focus on implementing the core ray tracing components. However, you also have the freedom to redesign the system as long as your ray tracer meets our requirements and produces the same images for the given scenes.
Requirement Overview
The programming portion of this assignment is described below.
A ray tracer computes images in image order, meaning that the outer loop visits pixels one at a time. (In our framework the outer loop is found in the class RayTracer). For each pixel it performs the following operations:
- Ray generation, in which the viewing ray corresponding to the current pixel is found. The calculations depend on the characteristics of the camera: where it is located, which way it is looking, etc. In our framework, ray generation happens in the subclasses of Camera.
- Ray intersection, which determines the visible surface at the current pixel by finding the closest intersection between the ray and a surface in the scene (in our framework, ray intersection is handled by the Scene class).
- Shading, in which the color of the object, as seen from the camera, is determined. Shading accounts for the effects of illumination and shadows (in our framework, shading happens in the subclasses of Shader).
- Spheres and triangle meshes
- Lambertian and Phong shading
- Point lights with shadows
- Parallel and perspective cameras
Your ray tracer will read files in an XML file format and output PNG images. We have split ray tracing in CS4620 into two parts. For now, you will implement basic ray tracing. Later in the semester, after you have learned many more graphics techniques, you will implement other features, such as advanced shaders, faster rendering, and transformations on groups of objects. In this document, we focus on what you need to implement the basic elements of a ray tracer.
Getting Started
A new commit has been pushed to the class Github page in the master branch. We recommend switching to your master branch, pulling this commit, and creating a new branch (e.g. A2 solution) and committing your work there. This new commit contains all the framework changes and additions necessary for this project.
Specification and Implementation
We have marked all the functions or parts of the functions you need to complete with TODO#A2 in the source code. To see all these TODO's in Eclipse, select Search menu, then File Search and type "TODO#A2". There are quite a few separate code snippets to complete in this assignment. To check your progress as you go along, we recommend implementation in the following order.
Cameras
An instance of the Camera class represents a camera in the scene. It must implement the following methods:
public void initView()This method sets an orthonormal basis for the camera based on the view and up directions. It should also set initialized to true.
public void getRay(Ray outRay, double inU, double inV)This method generates a new ray starting at the camera through a given image point and stores it in outRay. The image point is given in UV coordinates, which must first be converted into view coordinates. Recall that an orthographic camera produces rays with varying origin and constant direction, whereas a perspective camera produces rays with constant origin and varying direction.
You will implement these two methods for both the OrthographicCamera and the PerspectiveCamera. All of the properties you will need are stored in the Camera class.
You can then test your getRay() method for both of these classes by running the main method in Camera.java.
Surfaces
An instance of the Surface class represents a piece of geometry in the scene. It has to implement the following method:
boolean intersect(IntersectionRecord outRecord, Ray ray)
This method intersects the given ray with the surface. Return true if the ray intersects the geometry and write relevant information to the IntersectionRecord structure. Relevant information includes the position of the hit point, the surface normal at the hit point, the value t of the ray at the hit point, and the surface being hit itself. See the IntersectionRecord class for details.
We ask that you implement the intersection method for the following surfaces:
- Sphere: The class contains a 3D point center and a double radius. You will need to solve the sphere/ray intersection equations. Be sure to calculate the exact normal at the point of intersection and store it in the IntersectionRecord. See section 4.4.1 of the book.
- Triangle: In our system, each triangle belongs to a Mesh, which keeps a reference to a MeshData (the same data structure you used in the previous programming assignment). A triangle stores a vector index of 3 integers containing the indices of its three vertices. If the mesh does not have a per-vertex normal, the triangle stores the normal of the triangle in the norm field. See section 4.4.2 of the book. If the owning Mesh does not have a per-vertex normal, the intersect method should return the triangle normal stored in Triangle. If it does, it should interpolate the normals of the three vertices using the barycentric coordinate of the hit point.
Scene
The Scene class stores information relating to the composition, i.e. the camera, a list of surfaces, a list of lights, etc. It also contains a scene-file-specified exposure field, which can be used to adjust the brightness of the resulting image. You need to implement the following method:
boolean intersect(IntersectionRecord outRecord, Ray rayIn, boolean anyIntersection)
The method should loop through all surfaces in the scene (stored in the Surfaces field), looking for intersections along rayIn. This is done by calling the intersect method on each surface and it is used when a ray is first cast out into the scene. If anyIntersection is false, it should only record the first intersection that happens along rayIn, i.e. the intersection with the lowest value of t. If there is such an intersection, it is recorded in outRecord and true is returned; otherwise, the method returns false, and outRecord is not modified. If anyIntersection is true, the method may return true immediately upon finding any intersection with the scene's geometry, even without setting outRecord (this version is used to make shadow calculations faster).
Ray Tracing
You then need to complete the shadeRay method of the RayTracer class. This method contains the main logic of the ray tracer. It takes a ray generated by the camera, intersects it with the scene, and returns a color based on what the ray hits. Fortunately, most of the details are implemented in other methods; all you need to do is call those methods, and this should only take a few lines. For instance, the Scene class contains a method for finding the first object a given ray hits. Details are in the code's comments.
We have provided a normal shader that determines color based on the normal of the surface, as well as some sample scenes that use this shader. Once you have completed the previous sections, you should be able to render the scenes one-sphere-normals.xml and two-boxes-normals.xml correctly. See Appendix A for details on rendering scenes.
Shaders
A shader is represented by an instance of the Shader class. You need to implement the following method:
public void shade(Colord outIntensity, Scene scene, Ray ray, IntersectionRecord record)
which sets outIntensity (the resulting color) to the fraction of the light that comes from the incoming direction (omega_i)(i.e. the direction towards the light) and scatters out in direction (omega_o) (i.e., towards the viewer).
We ask you to implement two shaders:
- Lambertian: This class implements the perfectly diffuse shader. Its diffuse color k_d is specified by the diffuseColor field. The shade function should set
outIntensity to:
- k_d max ( n dot omega_i , 0 ) k_L/r^2
- Phong: This class implements the Blinn-Phong lighting model. It has a diffuse color component as defined above k_d, as well as specularColor k_s, and exponent p fields, where the exponent is the "shininess". The shade function should set outIntensity to:
-
(k_d max(n dot omega_i, 0) + k_s max(n dot h, 0)^p) k_L/r^2
Notice that these values should be computed once for each light in the scene, and the contributions from each light should be summed, unless something is blocking the path from the light source to the object. Shader.java contains a useful isShadowed() method to check this. Overall, the code for each shade method should look something like:
reset outIntensity to (0, 0, 0)
for each light in the scene
if !isShadowed(...)
compute color contribution from this light
add this contribution to outIntensity
end if
end for
After the shaders are completed, you should be able to render one-sphere.xml, two-boxes.xml, wire-box.xml, and the bunny scenes correctly.
Appendix A: Testing
The data directory contains scene files and reference images for the purpose of testing your code. Right click on the RayTracer file in Package Explorer, and choose Run As->Java Application. Without any command line arguments, the ray tracer will attempt to render all scenes in the default scene directory (i.e. data/scenes/ray1). If you want to render specific scenes, you can list the file names individually on the command line. This can be done from the Run dialog (Run Configurations). Choose the Arguments tab, and provide your command line arguments in Program arguments. Additionally, passing in a directory name will render all scenes in that directory.
Note that RayTracer prepends data/scenes/ray1 to its arguments. This means that you only need to provide a scene file name to render it. For example, if you give the argument one-sphere.xml to the RayTracer it will load the scene file data/scenes/ray1/one-sphere.xml and produce an output image in the same directory as the scene file.
If you would like to change the default scene location, there is a -p command line option that allows you to specify a different default path instead of using data/scenes/ray1.
Compare the images you have with the reference images, if there are visually significant differences, consider checking for bugs in your code.
Appendix B: Extra Credit
We've included a Cylinder subclass of Surface, similar to the Triangle and Sphere classes. The class contains center, a 3D point, and radius, height, both real numbers. Assume that the cylinder is capped, i.e., the top and bottom have caps (it is not a hollow tube). Also, assume it is aligned with the z-axis, and is centered around center;
i.e., if
center is (center_x, center_y, center_z), the cylinder's z-extent is from (center_z-height/2) to (center_z+height/2).
Your task is to implement the intersect method of a mathematical cylinder (NOT a meshed cylinder). Add an XML scene that includes a cylinder to test your implementation (See Appendix C for details on how this should be done--you shouldn't need to change any parser code).
Once this is done, try implementing a cylinder that is arbitrarily oriented. You will need to add two parameters, rotX and rotY, to specify the cylinder's rotation about the x and y axes. Note that this will require changing the coordinate system of the incoming ray within the intersect method to account for these rotations. After the coordinate system change, the math used to intersect the ray with the cylinder should be the same as its axis-aligned variant. Finally, build a test scene with a cylinder object.
Appendix C: Framework
This section describes the framework code that comes with the assignment. You do not need to spend time trying to understand it and it is not essential to read this to get started on the assignment. Instead, you can reference it as needed.
The framework for this assignment includes a simple main program, some utility classes for vector math, a parser for the input file format, and stubs for the classes that are required by the parser.
RayTracer
This class holds the entry point for the program. The main method is provided, so that your program will have a command-line interface compatible with ours. It treats each command line argument as the name of an input file, which it parses, renders an image, and writes the image to a PNG file. The method RayTracer.renderImage is called to do the actual rendering.
Image
This class contains an array of pixel colors (stored as doubles) and the requisite code to get and set pixels and to output the image to a PNG file.
egl.math package
This package contains classes to represent 2D and 3D vectors, as well as RGB colors. They support all the standard vector arithmetic operations you're likely to need, including dot and cross products for vectors and addition and scaling for colors.
Parser
The Parser class contains a simple parser based on Java's built-in XML parsing. The parser simply reads a XML document and instantiates an object for each XML entity, adding it to its containing element by calling set... or add... methods on the containing object.
For instance, the input:
<scene>
<surface type="Sphere">
<shader type="Lambertian">
<diffuseColor>0 0 1</diffuseColor>
</shader>
<center>1 2 3</center>
<radius>4</radius>
</surface>
</scene>
results in the following construction sequence:
- Create the scene.
- Create an object of class Sphere and add it to the scene by calling Scene.addSurface. This is OK because Sphere extends the Surface class.
- Create an object of class Lambertian and add it to the sphere using Sphere.setShader. This is OK because Lambertian extends the Shader class.
- Call setDiffuseColor(new Colord(0, 0, 1)) on the shader.
- Call setCenter(new Vector3d(1, 2, 3)) on the sphere.
- Call setRadius(4) on the sphere.
Which elements are allowed where in the file is determined by which classes contain appropriate methods, and the types of those methods' parameters determine how the tag's contents are parsed (as a number, a vector, etc.). There is more detail for the curious in the header comment of the Parser class.
The practical result of all this is that your ray tracer is handed an object of class Scene that contains objects that are in one-to-one correspondence with the elements in the input file. You shouldn't need to change the parser in any way.
What to Submit
Submit a zip file containing your solution organized the same way as the code on Github. Include a readme in your zip that contains:
- You and your partner's names and NetIDs.
- Any problems with your solution.
- Anything else you want us to know.
Exams
There will be an evening midterm and a final exam:
- Midterm: Oct 20th 2015, 7:30pm (Olin Hall 155)
- Final: Dec 10th, 2015, 7:00pm (Olin Hall 155, 165)
The exams are closed book, but you're allowed to bring one letter-sized piece of paper with writing on both sides, to avoid the need to memorize things.
Old Exams
Here are links to exams from previous versions of this class. They can be useful for studying, because they give an indication of the style and scope of problems that may be expected. Note that they are not a useful reference for topics to expect, because the content of the course has changed from year to year.
- CS 4620 Fall 2010
- CS 4620 Fall 2009
- CS 4620 Fall 2008
- CS 465 Fall 2005
- CS 465 Fall 2004
- CS 465 Fall 2003
About CS4620
Questions, help, discussion: The instructors are available to answer questions, advise on projects, or just to discuss interesting topics related to the class at office hours and by appointment as needed. For electronic communication we are using Piazza (handy link also at the top of this page).
Practicum: In the optional practicum course, CS4621/5621, you will get a more in-depth exposure to the course material and complete an additional project. Students taking the practicum will also be required to attend lectures every week during the Friday meeting time for CS4621/5621.
Academic integrity: We assume the work you hand in is your own, and the results you hand in are generated by your program. You are welcome to read whatever you want to learn what you need to do the work, but we do expect you to build your own implementations of the methods we are studying. If you are ever in doubt, just include a citation in your code or report indicating where some idea came from, whether it be a classmate, a web site, another piece of software, or anything—this always maintains your honesty, whether the source was used in a good way or not. The principle is that an assignment is an academic document, like a journal article. When you turn it in, you are claiming that everything in it is your original idea (or is original to you and your partner, if you are handing in as a pair) unless you cite a source for it.
School can be stressful, and your coursework and other factors can put you under a lot of pressure, but that is never a reason for dishonesty. If you feel you can't complete the work on your own, come talk to the professor or the TAs, or your advisor, and we can help you figure out what to do. Think before you hand in!
Clear-cut cases of dishonesty will result in failing the course.
For more information see Cornell's Code of Academic Integrity.
Collaboration: You are welcome (encouraged, even) to discuss projects among yourselves in general terms. But when it comes to writing up the homeworks or implementing the projects, you need to be working alone (or only with your partner if you are doing a project as a pair). In particular, it is never OK for you to see another student's homework writeup or another team's program code, and certainly never OK to copy parts of one person's or team's writeup, code, or results into another's, even if the general solution was worked out together. The paper and pencil parts of the projects can be discussed in general terms, but must be worked on alone.
Books
Textbook:
 |
Shirley & Marschner,
Fundamentals of Computer Graphicsthird edition |
Supplemental Books and Materials:
 |
Gortler,
Foundations of 3D Computer Graphicsfirst edition |
- OpenGL
"Red Book" --- *the* reference for OpenGL programming
- 3-D computer graphics: a mathematical introduction with OpenGL, Volume 385, By Samuel R. Buss
- Andrew S. Glassner, An Introduction to ray tracing,
1989