A2: Minifloat

Instructions: Remember, all assignments in CS 3410 are individual. You must submit work that is 100% your own. Remember to ask for help from the CS 3410 staff in office hours or on Ed! If you discuss the assignment with anyone else, be careful not to share your actual work, and include an acknowledgment of the discussion in a collaboration.txt file along with your submission.

The assignment is due via Gradescope at 11:59pm on the due date indicated on the schedule.

Submission Requirements

For this assignment, you will need to submit the following five files:

• minifloat.c, with your written implementation for the missing functions.
• minifloat_test_part1.expected, to match additional tests added in minifloat_test_part1.c
• Some additional tests, in:
  • minifloat_test_part1.c
  • minifloat_test_part2.c
  • minifloat_test_part3.c

Restrictions

For this assignment, you will build your own floating-point representation.

• You may not use built-in C operations for floating-point arithmetic.
• You may not cast data to float or double, or create variables with these types.

Provided Files

The provided release code contains seven files:

• minifloat.c, which includes some completed functions and some functions you are expected to implement
• minifloat.h, which provides declarations and comments for the functions in minifloat.c, including those you are to implement
• minifloat_test_part1.c, minifloat_test_part2.c, minifloat_test_part3.c, which provide some tests for you to get started. You are expected to add more tests of your own to each of these test suites
• minifloat_test_part1.expected, which provides a baseline file to help with testing part 1. You are expected to add more lines to this file as part of testing part 1.
• Makefile, which provides structure to compile your code (see our brief tutorial on Makefiles)

Getting Started

To get started, obtain the release code by cloning your assignment repository from GitHub:

$ git clone git@github.coecis.cornell.edu:cs3410-2025sp-student/<NETID>_minifloat.git

Replace <NETID> with your NetID. For example, if your NetID is zw669, then this clone statement would be git clone git@github.coecis.cornell.edu:cs3410-2025sp-student/zw669_minifloat.git

Overview

In this assignment, you will develop a custom minifloat data format in C. You will be expected to reason about floating-point details and implement operations over your custom floating-point data type in C.

Background

In class, we learned about floating-point numbers, which represent decimals with some number of bits. C has built-in float and double types, which use (on modern hardware) 32 bits and 64 bits, respectively. Increasing the number of bits in a floating-point representation gives it more precision and more dynamic range, at the expense of less efficient arithmetic. It can also be useful, however, to perform operations with smaller floating-point representations—trading off precision for potentially faster calculations.

In this assignment, you will implement functions for a specialized 8-bit floating-point type. We’ll call these 8-bit numbers minifloats. Minifloats have severely limited precision, but such tiny floating-point values are useful for situations where errors matter less and data sizes are enormous: most prominently, in machine learning. See, for example, this paper and this other paper that both show serious efficiency advantages from using 8-bit minifloats. While most floating-point formats enjoy built-in hardware support, we can also implement minifloats in software with bit packing tricks.

Minifloats follow a similar representation strategy to the standard IEEE floating-point types that we learned about in lecture. However, they differ in a few important ways to make the implementation simpler, which we will summarize as well.

Minifloat Specification

• Minifloats use 8 bits in total: 1 sign bit, 3 exponent bits, and 4 significand bits. The layout of a minifloat looks like this, with s for sign, e for exponent, and g for significand:

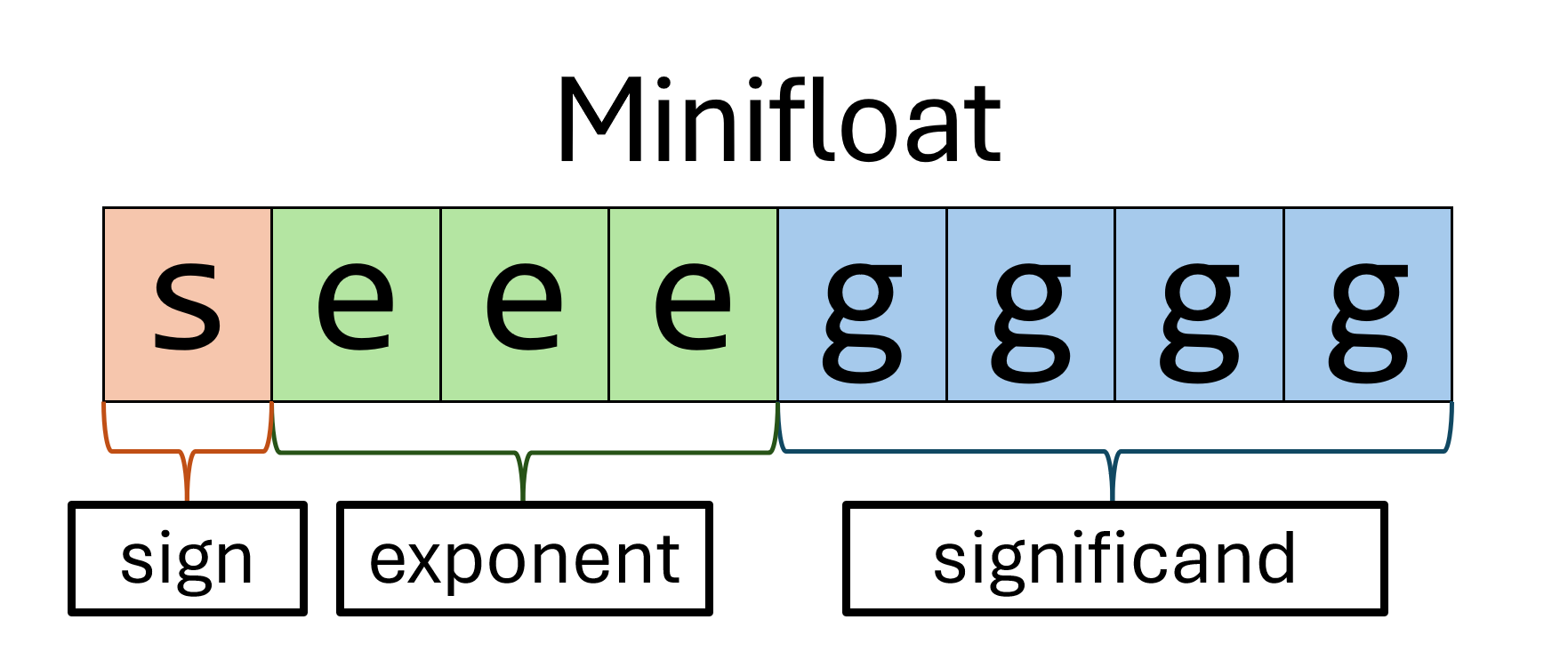
• As in standard formats, a sign bit of 0 indicates a positive number, and a sign bit of 1 indicates a negative number.

• Minifloats have a bias of 3. In other words, we subtract 3 from the bit-representation of a minifloat exponent. In comparison, single-precision floating-point numbers (i.e., float) have a bias of 127.

• Unlike standard floating-point formats, wherein we usually append a leading 1 to the significand bits with the $1.g$ notation, minifloats use the significand directly, with the binary point after the first digit. So if the four significand bits are $g_3 g_2 g_1 g_0$, then the “base” part of the represented value is the binary number $g_3 . g_2 g_1 g_0$. Or, in other words, the value is $g \times 2^{-3}$, where $g$ is the unsigned integer value of those 4 bits.

• Also unlike standard floating-point formats, our minifloats do not use special values: not a number (NaN) and infinity (+∞ and -∞).

All together, the value represented by a minifloat with sign $s$, exponent $e$, and significand $g$ is:

$$(-1)^s \times (g \times 2^{-3}) \times 2^{e - 3}$$

Or, equivalently, if you prefer to think of the significand’s representation in terms of bits:

$$(-1)^s \times (g_3.g_2g_1g_0) \times 2^{e - 3}$$

where $g_3$ is the significand’s most significant bit, $g_0$ is the least significant bit, and so on.

Examples

Now that we have defined our minifloat specification, let’s see some examples!

Example 1: 10111100

We have a sign of 1, an exponent of 011, and a signficand of 1100.

• Our sign bit 1 corresponds to $-1$.
• Our exponent 011 corresponds to a decimal exponent of $3-3 = 0$. (We’re applying our $-3$ bias here.)
• Our significand 1100 corresponds to the decimal $12 \times 2^{-3}=\frac{12}{8}=1.5$. (Or, equivalently, the significand corresponds to the binary number $1.100_2$, which is $1.5$ in decimal.)

Altogether, 10111100 is $-1 \times 1.5 \times 2^0 = -1 \times 1.5 \times 1 = -1.5$ in base-10.

Example 2: 00010010

We have a sign of 0, an exponent of 001, and a significand of 0010.

• Our sign 0 corresponds to $+1$.
• Our exponent 001 corresponds to a decimal exponent of $1-3 = -2$.
• Our significand 0010 corresponds indicates the binary value $0.010_{2}$, which equals $0.25_{10}$.

Altogether, 00010010 is $1 \times 0.25 \times 2^{-2} = \frac{1}{16} = 0.0625$ in base-10.

Converting between Minifloats and Decimals

Decimal to Minifloat

To convert a decimal number into a minifloat:

1. Convert the integer and fractional parts into binary.
2. Normalize to match the format $g_3.g_2g_1g_0 \times 2^e$.
3. Convert exponent into biased form (i.e., add 3).
4. Set the sign bit accordingly.

Example: Converting 2.25 into an 8-bit float

Step 1: Convert the integer and fractional parts to binary.

Converting the integer portion into binary yields 10.

Our fractional part is 0.25. To convert, multiply the fractional part by 2, record the integer part of the result (should be 0 or 1), and repeat with the new fractional part until the fractional part becomes 0 or the precision limit is reached (is 4 digits for our minifloat format). The recorded integer parts of this process becomes our binary representation for the original fractional part.

• $0.25 \times 2 = 0.50$. Record 0.
• $0.50 \times 2 = 1.00$. Record 1.

Thus our binary representation of 0.25 is 01. Together with the integer portion, our binary representation of 2.25 is 10.01.

Step 2: Normalize to match the format $g_3.g_2g_1g_0 \times 2^e$.

Now we normalize our result so that it fits the format $g_3.g_2g_1g_0 \times 2^e$. In this case, we shift to the left by one place: $1.001 \times 2^1$. From this we can see that our significand is 1001.

Step 3: Convert exponent into biased form (i.e., add 3).

Next, we need to apply our format’s exponent bias, which for minifloats is 3. To bias the exponent, we add our original exponent $e$ with the bias. So, $1 + 3 = 4$ (100 in binary).

Step 4: Set the sign bit accordingly.

Lastly, because 2.25 is positive, the sign bit should be set to 0.

Thus the minifloat representation of 2.25 is 01001001.

Minifloat to Decimal

To convert from a floating-point number into a decimal number:

1. Extract the sign, exponent, and significand.
2. Normalize the significand to the format $g_3.g_2g_1g_0$ and remove trailing zeros.
3. De-normalize to make the exponent 0.
4. Convert the integer and fractional parts to decimals.
5. Add a negative sign if necessary.

Example: Converting 11011100 into a Decimal

Step 1: Extract the sign, exponent, and significand.

• Sign bit: 1 (negative)
• Exponent: 101
• Significand: 1100

Step 2: Normalize the significand to the format $g_3.g_2g_1g_0$ and remove trailing zeros.

Our significand 1100 becomes 1.1.

Step 3: De-normalize to make the exponent 0.

We first convert our binary exponent 101 into base-10, yielding 5. We then subtract our bias (which is 3 for minifloats) from our exponent to get $5-3=2$.

Since our exponent is 2, we shift our binary point 2 places to the right, yielding 110.0.

Step 4: Convert the integer and fractional parts to decimals

Next, we convert the integer and fractional parts of 110.0 into base-10. Since $110_2 = 6_{10}$ and $0_2 = 0_{10}$, $110.0_{2} = 6.0_{10}$.

Step 5: Set the sign according to sign bit

Since the sign bit is 1, the final value is: $-6.0$.

Adding Minifloats

To perform addition with floating-point numbers:

1. Rewrite the smaller number so that the exponents are equal, and adjust the mantissa of the number with the smaller exponent by shifting it to the right accordingly.
2. Add the mantissas together.
3. Recombine and renormalize the result if necessary.

Example: $1.5 + 0.5$

First, we need to convert 1.5 and 0.5 into their minifloat representations. For 1.5 this is $1.1 \times 2^0$, and for 0.5 this is $1.0 \times 2^{-1}$.

Step 1: Adjust the mantissa

Because the exponents differ, we shift 0.5’s mantissa to the right by one: $1.0 \rightarrow 0.10$

Now both numbers have an exponent of 0.

Step 2: Add the mantissas together.

• $1.1_2 + 0.10_2 = 10.0_2$

Step 3: Recombine and renormalize the result if necessary

• $10.0_2 \times 2^0 = 1.0 \times 2^1$

Thus the answer is 0 100 1000 which is equivalent to 2.0 in base-10.

Bit size in C

We want to ensure that the type we are using to represent a minifloat is exactly 8 bits. We will use the uint8_t type from C’s stdint.h header. (We will avoid char, even though char is 8 bits on most platforms, because C unhelpfully does not guarantee that is is exactly 8 bits everywhere.) To break down this type’s, the uint means that bit-level operations are as on an unsigned integer, the 8 means that we expect operations to be on 8 bits, and _t is a common naming convention that indicates that this is a type. The stdint.h header defines many similar types, like these:

Your Task

This assignment is divided into three parts: displaying minifloats as decimals, implementing operations on minifloats, and using minifloats. Each part will have you implementing 1–3 functions, and adding test cases to help convince yourself these functions are correct. You must add at least 4 new test cases per function to what we have provided, though you may add more.

We have provided a mini_to_double utility function to help you with debugging and testing. You may not use this function in any of your submitted implementations, but you may use this function for writing test cases for any of your functions.

Part 1: Lab

View the lab slides here.

Review

If you need to, look over the lecture notes on standard floating-point types to remind yourself of the basic principles. And try out float.exposed to get hands-on practice!

Read over the background above and especially the specification for minifloats. To briefly summarize the minifloat format:

• Bit 7 is the sign bit
• Bits 6–4 are the exponent bits
• Bits 3–0 are the fraction bits

(Bits are numbered from the right, so 0 is the least significant bit.)

Displaying Minifloats

In this lab, your task is to implement a function for displaying minifloats in C, named print_mini. This function takes in a minifloat and must print the sign, whole number, and fractional part associated with this minifloat as a base-10 value. The exact specification, with examples, is given in minifloat.h. Your implementation should be filled into minifloat.c.

To make your task somewhat easier, we have written a concrete call to printf at the end of the each function that you may use as a guide for what to implement. Note that print_mini requires that we write 6 decimal digits—the provided printf specifier %06d will fill any integer to have preceding zeros such that the printed integer has 6 digits. To provide two concrete examples:

• printf("%06d", 123) will print 000123
• printf("%06d", 100000) will print 100000

Testing Part 1

A test script to help guide your development can be found in minifloat_test_part1.c. You can build this test with the following command:

rv make part1

To test this code, you must execute the resulting .out file and pipe your print results to a file, such as with the following command:

rv qemu minifloat_test_part1.out > minifloat_test_part1.txt

Finally, you must compare the resulting prints to our expected results using diff:

diff minifloat_test_part1.txt minifloat_test_part1.expected

If you observe any differences between the two, a printing test failed.

You can also combine these operations into a single bash command:

rv make part1 && rv qemu minifloat_test_part1.out > minifloat_test_part1.txt && diff minifloat_test_part1.txt minifloat_test_part1.expected

Reminder: You must add 4 new printing tests (which means modifying both minifloat_test_part1.c and minifloat_test_part1.expected).

Part 2: Minifloat Operations

Your second task is to implement an equality check, addition, and multiplication between minifloats. Specifically, you will be implementing mini_eq, mini_add, and mini_mul, which both take in two minifloats and produce a new minifloat. As before, the specifications for each function can be found in minifloat.h, and your implementation should be written in minifloat.c.

The results of the arithmetic operations mini_add and mini_mul must produce the minifloat value closest to adding together the corresponding real numbers. If there are two possible closest real numbers, your implementation must correspond to the closest real number further from zero than the result of addition. For example, we would round 2.125 to 2.25, and similarly -1.0625 to -1.125.

If there are multiple possible minifloat representations of the resulting real number, you must return the minifloat with the smallest exponent. For example, the minifloat value 0 011 0010 could be equivalently represented as 0 001 1000, and only the latter is considered correct for these arithmetic operations. Additionally, if an arithmetic operation would return 0, you must return exactly 00000000.

If applying addition or multiplication would result in a real number larger or smaller than can be represented by a minifloat, the result of these operations is undefined, and need not be tested.

Hint: If you become stuck on any of these functions, consider attempting another—each requires detail that can become more obvious while working on another.

Testing Part 2

Testing minifloat operations is more straightforward than testing the printing implemented earlier. We can simply run each test file and compare the resulting minifloats to expected values. To test part 2, you can directly build and execute part2:

rv make part2 && rv qemu minifloat_test_part2.out

Reminder: You must add 4 new tests per function.

Hint: Write as many edge-case tests as you can think of, there are many potential tricks with negative numbers and very small or very large minifloats.

Part 3: Using Minifloats

Your third task is a straightforward example use of the minifloats you have implemented. Specifically, you’ll be implementing functions to calculate the volume and surface area of a cylinder in the functions titled cylinder_volume and cylinder_area.

The volume and surface area of a cylinder depends on two variables, the radius r and height h of the cylinder, by the following equations:

• $\text{volume} = \pi \times r \times r \times h$
• $\text{surface area} = 2 \times \pi \times r \times (h + r)$

For reference and comparison, we have also written an implementation of these functions double_cylinder_volume and double_cylinder_area. These may be useful to refer to while implementing your own function, but are also used for the written task below.

For these implementations, you are expected to use the constant minifloat representation of PI to be 01001101 (representing 3.25), which is the closest minifloat to the decimal $\pi \approx 3.14159$. We have included this constant definition in minifloat.c for your convenience.

Testing Part 3

To test part 3, you can directly build and execute part3:

rv make part3 && rv qemu minifloat_test_part3.out

We have only provided you with a single simple test for each, and you should write at least 4 new tests. We test these particular functions by comparing our minifloat calculation to the result produced by calculating the same value with a double. We expect that the minifloat result (being less accurate) will have some error compared to the double representation, which in the test is represented by the threshold parameter.

We recommend trying out a few operations and seeing how difference there is between minifloat and double calculations, and adjusting your threshold accordingly. To help with comparing these operations, we use the provided mini_to_double utility function to calculate calculate a double value before and after computing the minifloat equivalent. (We do not define a double_to_mini conversion.)

Submission

Submit minifloat.c, minifloat_test_part1.expected, minifloat_test_part1.c, minifloat_test_part2.c, and minifloat_test_part3.c to Gradescope. Upon submission, we will provide a smoke test to ensure your code compiles and passes the public test cases.

Rubric

• 16 points: print_mini correctness
• 18 points: mini_eq correctness
• 16 points: mini_add correctness
• 19 points: mini_mul correctness
• 8 points: cylinder_area correctness
• 8 points: cylinder_volume correctness
• 15 points: test quality