We need to write some comments in module implementations to help code implementers and maintainers to reason about the code within the module. We'd like them to be able to reason about individual functions within the module in a local way, so they can judge whether each function is correctly implemented without thinking about every other function in the module. Last time we saw the abstraction function, which is essential to this process because it explains how information within the module is viewed abstractly by module clients.
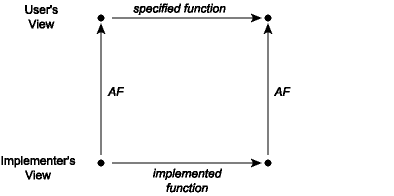
Using the abstraction function, we can now talk about what it means for an implementation of an abstraction to be correct. It is correct exactly when every operation that takes place in the concrete space makes sense when mapped by the abstraction function into the abstract space. This can be visualized as a commutation diagram:

A commutation diagram means that if we take the two paths around the diagram, we have to get to the same place. Suppose that we start from a concrete value and apply the actual implementation of some operation to it to obtain a new concrete value or values. When viewed abstractly, a concrete result should be an abstract value that is a possible result of applying the function as described in its specification to the abstract view of the actual inputs. For example, consider the union function applied to the concrete pair ([1,3],[2,2]), which would be the lower-left corner of the diagram. The result of this operation is the list [2,2,1,3], whose corresponding abstract value is the list {1,2,3}. Note that if we apply the abstraction function AF to the lists [1,3] and [2,2], we have the sets {1,3} and {2}. The commutation diagram requires that in this instance the union of {1,3} and {2} is {1,2,3}, which is of course true.
Some specifications, as we have seen, are nondeterministic: they do not fully specify the abstract behavior of the functions. For nondeterministic specifications there are several possible arrows leading from the abstract state at the upper left corner of the commutation diagram to other states. The commutation diagram is satisfied as long as the implemented function completes the diagram for any one of those arrows.
Recall the NATSET
interface for sets of natural numbers:
signature NATSET = sig
(* Overview: A "set" is a set of natural numbers:
e.g., {1,11,0}, {}, and {1001} *)
type set
(* empty is the empty set *)
val empty : set
(* single(x) is {x}. Requires: x >= 0 *)
val single : int -> set
(* union is set union. *)
val union : set*set -> set
(* contains(x,s) is whether x is a member of s *)
val contains: int*set -> bool
(* size(s) is the number of elements in s *)
val size: set -> int
end
As discussed last time, in an implementation of this interface we need an
abstraction function. We talked about three different implementations: a list
of integers with no duplicates (NatSetNoDups),
a list of integers possibly with duplicates (NatSet),
and a vector of booleans. Each has its own abstraction function, but we
can use the same abstraction function for the first two:
(* Abstraction function: the list [a1,...,an] represents the * smallest set containing all of the elements a1,...,an. * The empty list represents the empty set. *)
Consider how we might write the size function in each of
these implementations. For the list of integers with no duplicates
(NatSetNoDups), the size is just the length of the list:
val size = List.length
But for the representation of a list of integers with possible duplicates
(NatSet) we need to make sure we don't double-count
any duplicate elements:
fun size(lst) = case lst of [] => 0 | h::t => size(t) + (if contains(t, h) then 0 else 1)
How we know that we don't need to do this check in NatSetNoDups?
After all, the type of the representation is exactly the same:
int list. And the abstraction function is identical.
What is different is that if an int list represents
a NatSetNoDups.set, it cannot have any duplicate elements.
Because the code doesn't say this, implementers will not be able
to reason locally about whether functions like size are implemented
correctly.
If we think about this in terms of the commutation diagram, we see that
the abstraction function is not enough. Consider taking the size of the
set {2}. The abstraction function maps the
representation [2,2] to this set. But the abstract size
operation on the set gives size({2}) = 1, whereas
the NatSetNoDups implementation computes size([2,2]) = 2.
We can fix this by adding a second piece of information to the implementation:
the representation invariant (or rep invariant, or RI). The
rep invariant defines what concrete data values are valid representations
(reps) of abstract values. For NatSetNoDups, a valid
representation must satisfy the following condition:
structure NatSetNoDups = struct
type set = int list
(* Abstraction function: the list [a1,...,an] represents the set
* {a1,...,an}. [] represents the empty set.
* Representation invariant: given the rep [a_1,...,a_n],
* no elements are negative, and no two elements are equal. *)
We write this along with the abstraction function:
(* Representation invariant: given the rep [a_1,...,a_n], * no elements are negative, and no two elements are equal. *)
The rep invariant holds for any valid representation.
Therefore, a value of the representation type that does not satisfy
the rep invariant does not correspond to
implementation structures that must be maintained at all times. Structures that
do not satisfy this constraint are invalid; they do not correspond (via the
abstraction function) to any abstract type. The correct functioning of
implemented operations depend on such constraints. For instance, The
NatSetNoDups implementation requires no duplicates in the list. If this
constraint is broken, functions such as size() will not return the
correct answer. Here is an example of how to document the rep invariant
for the NatSetNoDups implementation:
The rep invariant is a condition that is intended to hold for all values of the abstract type (e.g., set). Therefore, in implementing one of the operations of the abstract data type, it can be assumed that any arguments of the abstract type satisfy the rep invariant.
We observed earlier that the abstraction function may be a partial function. In
fact, in the case of both NatSet and NatSetNoDups, the
abstraction function is partial because it maps lists containing negative
integers (such as [-1,1]) to sets that are not part of the space of
abstract values. In order to make sure that an implementation works—that it
completes the commutation diagram—it had better be the case that the
implementation never produces any concrete values that do not map to abstract
values.
The role of the representation invariant is to restrict the domain of the abstraction function to those values on which the implementation is going to work properly. The relationship between the representation invariant and the abstraction function is depicted in this figure:

The rep invariant is a condition that is intended to hold for all values of the abstract type (e.g., set). Therefore, in implementing one of the operations of the abstract data type, it can be assumed that any arguments of the abstract type satisfy the rep invariant. This assumption restores local reasoning about correctness, because we can use the rep invariant and abstraction function to judge whether the implementation of a single operation is correct in isolation from the rest of the module. It is correct if, assuming that:
we can show that
The rep invariant makes it easier to write code that is provably correct,
because it means that we don't have to write code that works for all possible
incoming concrete representations--only those that satisfy the rep invariant.
This is why NatSetNoDups.union doesn't have to work on lists that
contain duplicate elements. On return there is a corresponding responsibility to
produce only values that satisfy the rep invariant. As suggested in the figure
above, the rep invariant holds for all reps both before and after the functions,
which is why we call it an invariant at all.
When implementing a complex abstract data type, it is often helpful to write
a function internal to the module that checks that the rep invariant holds. This
function can provide an additional level of assurance about your reasoning the
correctness of the code. By convention we will call this function repOK;
given an abstract type (say, set) implemented as a concrete type
(say, int list) it always has the same specification:
(* Returns whether x satisfies the representation invariant *) fun repOK(x: int list): bool = ...
The repOK can be used to help us implement a module and be sure
that each function is independently correct. The trick is to bulletproof
each function in the module against all other functions by having it apply repOK
to any values of the abstract type that come from outside. In addition, if it
creates any new values of the abstract type, it applies repOK to
them to ensure that it isn't breaking the rep invariant itself. With this
approach, a bug in one function is less likely to create the appearance of a bug
in another.
A more convenient way to write repOK is to make it an identity
function that
raises an exception if the rep invariant doesn't hold. Making it an identity
function lets us conveniently test the rep invariant in various ways, as shown
below.
(* The identity function. * Checks whether x satisfies the representation invariant. *) fun repOK(x: int list): int list = ...
Here is an example of we might use repOK for the NatSetNoDups
implementation of sets given in lecture. Notice that repOK is
applied to all sets that are created. This ensures that if a bad
set representation is created, it will be detected immediately. In case
we somehow missed a check on creation, we also apply repOK to
all incoming set arguments. If these is a bug, these checks will make help
us quickly figure out where the rep invariant is being broken.
structure NatSetNoDups :> NATSET = struct
type set = int list
(* AF: the list [a1,...,an] represents the set {a1,...,an}.
* RI: list contains no negative elements or duplicates.
*)
fun contains_internal(x:int,s:int list) =
case s of
[] => false
| h::t => x = h orelse contains_internal(x,t)
fun repOK(s: int list): int list =
case s of
[] => s
| h::t => if h >= 0 andalso not(contains_internal(h,repOK(t)))
then s
else raise Fail "RI failed"
val empty = []
fun single(x) = repOK([x])
fun contains(x,s) = contains_internal(repOK(s))
fun union(s1, s2) =
repOK (foldl (fn (x,s) =>
if contains(x,s) then s else x::s)
(repOK(s1)) (repOK(s2)))
fun size(s) = length(repOK(s))
end
Here, repOK is implemented using contains_internal
rather than the function contains, because using contains would
result in a lot of extra repOK checks. Writing an unchecked
helper function like this is a common pattern when implementing a
repOK check. Fortunately we can reuse contains_internal
when implementing the real contains.
Calling repOK on every argument can be too
expensive for the production version of a program. The repOK above
is quite expensive (though it could be implemented more cheaply). For
production code it may be more appropriate to use a version of
repOK that only checks the parts of the rep invariant that are
cheap to check. When there is a requirement that there be no run-time cost,
repOK can be changed to an identity function (or macro) so the
compiler optimizes away the calls to it. Howver, it is a good idea to keep
around the full code of repOK (perhaps in a comment) so it can be
easily reinstated during future debugging.
Invariants on data are useful even when writing modules that are not easily considered to be providing abstract data types. Sometimes it is difficult to identify an abstract view of data that is provided by the module, and there may not be any abstract type at all. Invariants are important even without an abstraction function, because they document the legal states and representations that the code is expected to handle correctly. In general we refer to module invariants as invariants enforced by modules. In the case of an ADT, the rep invariant is a module invariant. Module invariants are useful for understanding how the code works, and also for maintenance, because the maintainer can avoid changes to the code that violate the module invariant.
A strong module invariant is not always the best choice, because it restricts future changes to the module. We described interface specifications as a contract between the implementer of a module and the user. A module invariant is a contract between the implementer and herself, or among the various implementers of the module, present and future. According to assumption 2, above, ADT operations may be implemented assuming that the rep invariant holds. If the rep invariant is ever weakened (made more permissive), some parts of the implementation may break.Thus, one of the most important purposes of the rep invariant is to document exactly what may and what may not be safely changed about a module implementation. A weak invariant forces the implementer to work harder to produce a correct implementation, because less can be assumed about concrete representation values, but conversely it gives maximum flexibility for future changes to the code.
Let us consider the rep invariant for the vector implementation of NATSET.
There is some question about what we should write. One possibility is to write
the strongest possible specification of the possible values that can be created
by the implementation. It happens that the vector representing the set never has
trailing false values:
structure NatSetVec :> NATSET = struct type set = bool vector (* Abstraction function: the vector v represents the set of all natural numbers i such that sub(v,i) = true Representation invariant: the last element of v is true *) val empty:set = Vector.fromList []
This representation invariant describes an interesting property of the
implementation that may be useful in judging its performance. However, we don't
need this rep invariant in order to show that the implementation is correct. If
there were no rep invariant, we could still argue that the implementation works
properly. All of the operations of NatSetVec will work even if sets
are somehow introduced that violate the no-trailing-false property. It is not
necessary to have the rep invariant in order to argue that the operations of NatSetVec
are correct according to the 4-point plan above.
A sign of good code design is that invariants on program data are enforced in a localized way, within modules, so that programmers can reason about whether the invariant is enforced without thinking about the rest of the program. To do this it is necessary to figure out just the right operations to be exposed by the various modules, so that useful functionality can be provided while also ensuring that invariants are maintained.
Conversely, a common design error is to break up a program into a set of modules that simply encapulate data and provide low-level accessor operations, while putting all the interesting logic of the program in one main module. The problem with this design is that all the interesting (and hard!) code still lives in one place, and the main module is responsible for enforcing many complex invariants among the data. This kind of design does not break the program into simpler parts that can be reasoned about independently.It shows the big danger sign that the abstractions aren't right: all the code is either boring code, or overly complex code that is hard to reason about. It is a kind of fake modularity.
For example, suppose we are implementing a graphical chess game. The game state includes a board and a bunch of pieces. We might want to keep track of where each piece is, as well as what is on each board square. And there may be a good deal of state in the graphical display too. A good design would ensure that the board, the pieces, and the graphical display stay in sync with each other in code that is separate from that which handles the detailed rules of the game of chess.