Dijkstra's algorithm

A* search
If we are trying to find a path to a particular vertex in a weighted graph, we can often do better than Dijkstra's algorithm. Dijkstra's algorithm greedily visits nodes in order of increasing distance from the initial vertex. Imagine trying to implement the MapQuest service: the algorithm will spend as much time exploring nodes that are along the optimal path as it does on exploring nodes that are in the opposite direction from the desired goal—nodes that are almost certainly not going be on the optimal path to the destination. This is because Dijkstra's algorithm doesn't take into account where the destination node is.
The A* search algorithm (pronounced “A-star”) is a refinement to the shortest path algorithm that directs the search towards the desired goal rather than exploring nodes based simply on distance from the initial vertex. This is useful for implementing services like MapQuest and also for many other search problems. The key idea is to define a heuristic function h(v) that estimates how far a given vertex v is from the goal vertex. Rather than just trying to minimize the distance from the initial vertex, we then run Dijkstra's shortest path algorithm with the notion of distance defined as the sum of the real distance and the heuristic function. That is, when picking a vertex to dequeue, rather than choosing the current minimum distance, the algorithm chooses the vertex that minimizes the sum h(v) + dist(v).
Imagine what happens if the heuristic function is perfectly accurate, meaning that it correctly estimates the remaining distance from the node v to the desired goal. In this case, all of the nodes along the optimum path have exactly the same value for distance+heuristic. Therefore they will be dequeued sequentially off the priority queue without any other nodes being considered, because at every step, a node on the path will be the current minimum. So the optimal path will be found as efficiently as is possible. Of couse, perfectly accurate heuristic functions are not feasible in general. But even an approximately correct heuristic function can improve search performance dramatically.
It is helpful to visualize the shape of the frontier constructed by the ordinary Dijkstra's algorithm versus A* with a good heuristic function. Imagine that we are trying to find a path in the plane, which is covered densely with random nodes connected to nearby neighbors, and where there are obstacles to avoid. An obvious choice for a heuristic function is Euclidean (straight-line) distance, which we know can never overestimate the distance, but might underestimate it if there is an obstacle to avoid on the line between the current node and the destination.

Dijkstra's algorithm

A* search
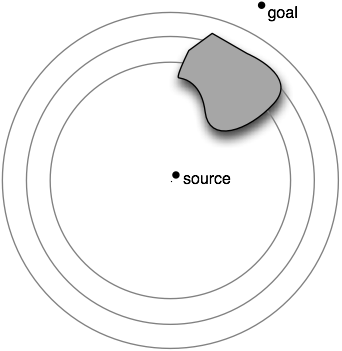
Dijkstra explores the plane in order of distance from the source, growing a circle of visited nodes:
By contrast, A* will explore directly on a line toward the destination, and when it runs into an obstacle, will explore progressively larger ellipses with foci at the source and destination, because an ellipse is the set of points where the sum of the distance already taken plus the estimated distance yet to go (the heuristic) is a constant.
Ideally, a heuristic function satisfies two properties:
If we think about it, we realize that the A* algorithm is really just Dijkstra's algorithm in disguise. An instance of A* can be converted into Dijkstra's algorithm by changing the weight w(v,v') of every edge from v to v' to be w(v,v') + h(v') - h(v). The differences in heuristic will cancel as we sum them along any path, so the distance along any path in this graph from the source to a vertex v is dist(v) + h(v). Since h(goal) = 0, the total distance from the source to the goal is the same in both graphs. As long as the heuristic function is monotonic, the edges in this new graph have nonnegative weights, and Dijkstra's algorithm works correctly.
In practice, for some search problems it is necessary to sacrifice monotonicity and even admissibility. This can happen because the admissible heuristics are too conservative to be effective at guiding the search. If this is the case, Dijkstra's algorithm won't quite work. If the heuristic is not monotonic, there are edges with negative weights. However, the shortest-path algorithm can be modified to ensure that the optimum path is found: when a shorter path is found to a completed node, that node must be pushed back onto the priority queue. And searching cannot finish once the goal is the closest node on the frontier; instead, it must continue until the closest node on the frontier has a distance larger than the maximum amount by which the heuristic function can overestimate.
A* search is useful not only for motion planning and path finding problems, but also for more general single-player search problems where one might think to use a depth-first search instead. A* can be much more efficient with a good heuristic function, though it tends to use a lot more memory than DFS. There are also depth-first search techniques that exploit the same insight as A*, to explore more deeply along promising paths.