So far we've been programming as though all pointers between boxes are equally expensive to follow. This turns out not to be even approximately true. Our simple model of how the computer memory works was that the processor generates requests to the memory that include a memory address. The memory looks up the appropriate data and sends it back to the processor. Computers used to work this way, but these days processors are so much faster than memory that something else is needed. A typical computer memory these days takes about 60ns to deliver requested data. This sounds pretty fast, but you have to keep in mind that a 2GHz processor is doing a new instruction every 0.5ns. Thus, the computer will have to wait for about 100 cycles every time the memory is needed to deliver data.
This problem is solved by sticking smaller, faster memory chips in between the processor and the main memory. These chips are called a cache : a cache keeps track of the contents of memory locations that were recently requested by the processor. Because the cache is much smaller than main memory (hundreds of kilobytes instead of tens or hundreds of megabytes), it can be made to deliver requests much faster than main memory: in tens of cycles rather than hundreds. In fact, one level of cache isn't enough. Typically there are two or three levels of cache, each smaller and faster than the next one out. The primary cache is the fastest cache, usually right on the processor chip and able to serve memory requests in one or two cycles. The secondary cache is larger and slower. Tertiary caches, if used, are usually off-chip.
For example, the next-generation Intel processor (McKinley) has three levels of cache right on the chip, with increasing response times (measured in processor cycles) and increasing cache size. The result is that almost all memory requests can be satisfied without going to main memory.
Having caches only helps if when the processor needs to get some data, it is already in the cache. Thus, the first time the processor access the memory, it must wait for the data to arrive. On subsequent reads from the same location, there is a good chance that the cache will be able to serve the memory request without involving main memory. Of course, since the cache is much smaller than the main memory, it can't store all of main memory. The cache is constantly throwing out information about memory locations in order to make space for new data. The processor only gets speedup from the cache if the data fetched from memory is still in the cache when it is needed again. When the cache has the data that is needed by the processor, it is called a cache hit. If not, it is a cache miss. The ratio of the number of hits to misses is called the cache hit ratio. Because memory is so much slower than the processor, the cache hit ratio is critical to overall performance.
Caches improve performance when memory accesses exhibit: reads from memory tends to request the same locations repeatedly, or at least memory locations near previous requests. A tendency to revisit the same or nearby locations is known as locality. Computations that exhibit locality will have a relatively high cache hit ratio. Note that caches actually store chunks of memory rather than individual words of memory. So a series of memory reads to nearby memory locations are likely to mostly hit in the cache. When there is a cache miss, a whole sequence of memory words is requested from main memory at once, because it is cheaper to read memory that way. The cache records cached memory locations in units of cache lines whose size depends on the size of the cache (typically 4-32 words).
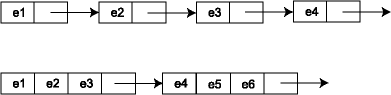
How does this affect us as programmers? We would like to write code that has good locality to get the best performance. This has implications for many of the data structures we have looked at. For example, we talked about how to implement hash tables using linked lists to represent the buckets. Linked lists involve chasing a lot of pointers, which means they have poor locality. A given linked list node probably doesn't even fill up one cache line. When the node is accessed, the whole cache line is fetched from main memory, yet it is mostly not used.
For best performance, you should figure out how many elements can be fit sequentially into a single cache line. The representation of a bucket set is then a linked list where each node in the linked list contains several elements (and a chaining pointer) and takes up an entire cache line. Thus, we go from a linked list that looks like the one on top to the one on the bottom:

Doing this kind of performance optimization can be tricky in a language like SML where the language is working hard to hide these kind of low-level representation choices from you. In languages like C, C++, or Modula-3, you have the ability to control memory layout somewhat better. A rule of thumb, however, is that SML records and tuples are stored contiguously in memory. So this kind of memory layout can be implemented in SML, e.g.:
datatype bucket = Empty | Bucket of elem * bucket (* poor locality *)
datatype big_bucket =
BigEmpty
| Bucket of {e1: elem, e2: elem, e3: elem, next: big_bucket} (* better locality *)
The same idea can be applied to trees. Binary trees are not good for locality because a given node of the binary tree probably occupies only a fraction of a cache line. B-trees are a way to get better locality. As in the hash table trick above, we store several elements in a single node -- as many as will fit in a cache line.
B-trees were originally invented for storing data structures on disk, where locality is even more crucial than with memory. Accessing a disk location takes about 5ms = 5,000,000ns. Therefore if you are storing a tree on disk you want to make sure that a given disk read is as effective as possible. B-trees, with their high branching factor, ensure that few disk reads are needed to navigate to the place where data is stored. B-trees are also useful for in-memory data structures because these days main memory is almost as slow relative to the processor as disk drives were when B-trees were introduced!
A B-tree of order m is a search tree where each nonleaf node has up to m children. The actual elements of the collection are stored in the leaves of the tree. The data structure satisfies several invariants:
For example, the following is an order-5 B-tree (m=5) where the leaves have enough space to store up to 3 data records:
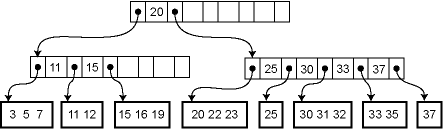
Because the height of the tree is uniformly the same and every node is at least half full, we are guaranteed that the asymptotic performance is O(lg n) where n is the size of the collection. The real win is in the constant factors, of course. We can choose m so that the pointers to the m children plus the m−1 elements fill out a cache line at the highest level of the memory hierarchy where we can expect to get cache hits. For example, if we are accessing a large disk database then our "cache lines" are memory blocks of the size that is read from disk.
Lookup in a B-tree is straightforward. Given a node to start from, we use a simple linear or binary search to find whether the desired element is in the node, or if not, which child pointer to follow from the current node.
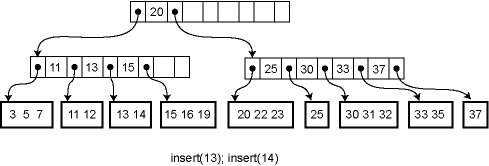
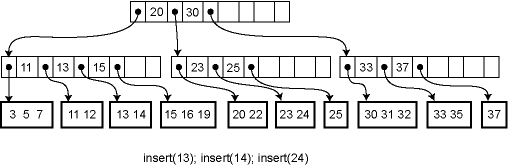
Insertion and deletion from a B-tree are more complicated; in fact, they are notoriously difficult to implement correctly. For insertion, we first find the appropriate leaf node into which the inserted element falls (assuming it is not already in the tree). If there is already room in the node, the new element can be inserted simply. Otherwise the current leaf is already full and must be split into two leaves, one of which acquires the new element. The parent is then updated to contain a new key and child pointer. If the parent is already full, the process ripples upwards, eventually possibly reaching the root. If the root is split into two, then a new root is created with just two children, increasing the height of the tree by one.
For example, here is the effect of a series of insertions. The first insertion merely affects a leaf. The second insertion overflows the leaf and adds a key to an internal node. The third insertion propagates all the way to the root.

Deletion works in the opposite way: the element is removed from the leaf. If the leaf becomes empty, a key is removed from the parent node. If that breaks invariant 3, the keys of the parent node and its immediate right (or left) sibling are reapportioned among them so that invariant 3 is satisfied. If this is not possible, the parent node can be combined with that sibling, removing a key another level up in the tree and possible causing a ripple all the way to the root. If the root has just two children, and they are combined, then the root is deleted and the new combined node becomes the root of the tree, reducing the height of the tree by one.
Further reading: Aho, Hopcroft, and Ullman, Data Structures and Algorithms, Chapter 11.
A splay tree is an efficient implementation of binary search trees that takes advantage of locality in the incoming lookup requests. Locality in this context is a tendency to look for the same element multiple times. A stream of requests exhibits no locality if every element is equally likely to be accessed at each point. For many applications, there is locality, and elements tend to be accessed repeatedly. A good example of an application with this property is a network router. Routers must decide on which outgoing wire to route the incoming packets, based on the IP address in the packets. The router needs a big table (a map) that can be used to look up an IP address and find out which outgoing connection to use. If an IP address has been used once, it is likely to be used again, perhaps many times. Splay trees are designed to provide good performance in this situation.
In addition, splay trees offer amortized O(lg n) performance. That is, a sequence of M operations on an n-node splay tree takes O(M lg n) time.
A splay tree is a binary search tree. It has one interesting difference, however: whenever an element is looked up in the tree, the splay tree reorganizes to move that element to the root of the tree, without breaking the binary search tree invariant. If the next lookup request is for the same element, it can be returned immediately. In general, if a small number of elements are being heavily used, they will tend to be found near the top of the tree and are thus found quickly.
We have already seen a way to move an element upward in a binary search tree: tree rotation. When an element is accessed in a splay tree, tree rotations are used to move it to the top of the tree. This simple algorithm can result in extremely good performance in practice. Notice that the algorithm requires that we be able to update the tree in place, but the abstract view of the set of elements represented by the tree does not change and the rep invariant is maintained. This is an example of a benevolent side effect: a side effect that does not change the abstract view of the value represented.
There are three kinds of tree rotations that are used to move elements upward in the tree. These rotations have two important effects: they move the node being splayed upward in the tree, and they also shorten the path to any nodes along the path to the splayed node. This latter effect means that splaying operations tend to make the tree more balanced.
The simple tree rotation used in AVL trees and treaps is also applied at the root of the splay tree, moving the splayed node x up to become the new tree root. Here we have A < x < B < y < C, and the splayed node is either x or y depending on which direction the rotation is. It is highlighted in red.
y x / \ / \ x C <-> A y / \ / \ A B B C
Lower down in the tree rotations are performed in pairs so that nodes on the path from the splayed node to the root move closer to the root on average. In the "zig-zig" case, the splayed node is the left child of a left child or the right child of a right child ("zag-zag").
z x
/ \ / \
y D A y
/ \ <-> / \ (A < x < B < y < C < z < D)
x C B z
/ \ / \
A B C D
In the "zig-zag" case, the splayed node is the left child of a right child or vice-versa. The rotations produce a subtree whose height is less than that of the original tree. Thus, this rotation improves the balance of the tree. In each of the two cases shown, y is the splayed node:
z x y
/ \ / \ / \
y D / \ A z (A < y < B < x < z < D)
/ \ -> y z <- / \
A x / \ / \ x D
/ \ A B C D / \
B C B C
See this page for a nice visualization of splay tree rotations and a demonstration that these rotations tend to make the tree more balanced while also moving frequently accessed elements to the top of the tree.
Here is SML code for splay trees. The key function is splay, which takes a non-leaf node and a key k to look for, and returns a node that is the new top of the tree. The element whose key is k, if it was present in the tree, is the value of the returned node. If it was not present in the tree, a nearby value is in the node.
functor SplayTree(structure Params : ORDERED_SET_PARAMS)
:> ORDERED_FUNCTIONAL_SET where type key = Params.key and
type elem = Params.elem =
struct
type key = Params.key
type elem = Params.elem
val compare = Params.compare
val keyOf = Params.keyOf
datatype tree =
Empty
| Node of tree * elem * tree
type node = tree * elem * tree
(* Representation invariant:
* All values in the left subtree are less than "value", and
* all values in the right subtree are greater than "value".
*)
type set = int * (tree ref)
(* Representation invariant: size is the number of elements in
* the referenced tree. *)
fun empty() = (0, ref Empty)
(* splay(n,k) is a BST node n' where n' contains all the
* elements that n does, and if an element keyed by k is in under n',
* #value n is that element.
* Requires: n satisfies the BST invariant.
*)
fun splay((L, V, R), k: key): node =
case compare(k, keyOf(V))
of EQUAL => (L, V, R)
| LESS =>
(case L
of Empty => (L, V, R) (* not found *)
| Node (LL, LV, LR) =>
case compare(k, keyOf(LV))
of EQUAL => (LL, LV, Node(LR, V, R)) (* 1: zig *)
| LESS =>
(case LL
of Empty => (LL, LV, Node(LR, V, R)) (* not found *)
| Node n => (* 2: zig-zig *)
let val (LLL, LLV, LLR) = splay(n,k) in
(LLL,LLV,Node(LLR,LV,Node(LR,V,R)))
end)
| GREATER =>
(case LR
of Empty => (LL, LV, Node(LR, V, R))
| Node n => (* 3: zig-zag *)
let val (RLL, RLV, RLR) = splay(n,k) in
(Node(LL,LV,RLL),RLV,Node(RLR,V,R))
end))
| GREATER =>
(case R
of Empty => (L, V, R) (* not found *)
| Node (RL, RV, RR) =>
case compare(k, keyOf(RV))
of EQUAL => (Node(L,V,RL),RV,RR) (* 1: zag *)
| GREATER =>
(case RR
of Empty => (Node(L,V,RL),RV,RR) (* not found *)
| Node n => (* 3: zag-zag *)
let val (RRL, RRV, RRR) = splay(n,k) in
(Node(Node(L,V,RL),RV,RRL),RRV,RRR)
end)
| LESS =>
(case RL
of Empty => (Node(L,V,RL),RV,RR) (* not found *)
| Node n => (* 2: zag-zig *)
let val (LRL, LRV, LRR) = splay(n,k) in
(Node(L,V,LRL),LRV,Node(LRR,RV,RR))
end))
fun lookup((size,tr),k) =
case !tr of
Empty => NONE
| Node n =>
let val n' as (L,V,R) = splay(n,k) in
tr := Node n';
if compare(k, keyOf(V)) = EQUAL then SOME(V)
else NONE
end
fun add((size,tr):set, e:elem) = let
val (t', b) = add_tree(!tr, e)
val t'': node = splay(t', keyOf(e))
val size' = if b then size else size+1
in
((size', ref (Node(t''))),b)
end
and add_tree(t: tree, e: elem): node * bool =
case t
of Empty => ((Empty, e, Empty), false)
| Node (L,V,R) =>
(case compare (keyOf(V),keyOf(e))
of EQUAL => ((L,e,R),true)
| GREATER => let val (n',b) = add_tree(L, e) in
((Node(n'),V,R),b)
end
| LESS => let val (n',b) = add_tree(R, e) in
((L,V,Node(n')),b)
end)
...
end
To show that splay trees deliver the promised amortized performance, we define a potential function to keep track of the extra time that can be consumed by later operations on the tree. The idea is that for any given tree T, there is a function Φ(T) that is that tree's potential. We then define the amortized time taken by a single tree operation that changes the tree from T to T' as the actual time t, plus the change in potential Φ(T')-Φ(T). Now consider a sequence of M operations on a tree, taking actual times t1, t2, t3, ..., tM and producing trees T1, T2, ... TM. The amortized time taken by the operations is the sum of the actual times for each operation plus the sum of the changes in potential: t1 + t2 + ... tM + (Φ(T2)−Φ(T1)) + (Φ(T3) − Φ(T2)) + ... + (Φ(TM) − Φ(TM-1)) = t1 + t2 + ... tM + Φ(TM) − Φ(T1). Therefore the amortized time for a sequence of operations is an underestimate of the actual time by the amount of the drop in the potential function Φ(TM) − Φ(T1) seen over the whole sequence of operations.
The key to amortized analysis is to define the right potential function. Given a node x in a binary tree, let size(x) be the number of nodes below x (including x). Let rank(x) be the binary logarithm of size(x). Then the potential Φ(T) of a tree T is the sum of the ranks of all of the nodes in the tree. Note that if a tree has n nodes in it, the maximum rank of any node is lg n, and therefore the maximum potential of a tree is n lg n. This means that over a sequence of operations on the tree, its potential can decrease by at most n lg n. So the correction factor to amortized time is at most lg n, which is good.
Now, let us consider the amortized time of an operation. The basic operation of splay trees is splaying; it turns out that for a tree t, any splaying operation on a node x takes at most amortized time 3*rank(t) + 1. Since the rank of the tree is at most lg(n), the splaying operation takes O(lg n) amortized time. Therefore, the actual time taken by a sequence of n operations on a tree of size n is at most O(lg n) per operation.
To obtain the amortized time bound for splaying, we consider each of the possible rotation operations, which take a node x and move it to a new location. We consider that the rotation operation itself takes time t=1. Let r(x) be the rank of x before the rotation, and r'(x) the rank of node x after the rotation. We will show that simple rotation takes amortized time at most 3(r'(x) − r(x))) + 1, and that the other two rotations take amortized time 3(r'(x) − r(x)). There can be only one simple rotation (at the top of the tree), so when the amortized time of all the rotations performed during one splaying is added, all the intermediate terms r(x) and r'(x) cancel out and we are left with 3(r(t) − r(x)) + 1. In the worst case where x is a leaf and has rank 0, this is equal to 3*r(t) + 1.
The only two nodes that change rank are x and y. So the cost is 1 + r'(x) − r(x) + r'(y) − r(y). Since y decreases in rank, this is at most 1 + r'(x) − r(x). Since x increases in rank, r'(x) − r(x) is positive and this is bounded by 1 + 3(r'(x) − r(x)).
Only the nodes x, y, and z change in rank. Since this is a double rotation, we assume it has actual cost 2 and the amortized time is
2 + r'(x) − r(x) + r'(y) − r(y) + r'(z) − r(z)
Since the new rank of x is the same as the old rank of z, this is equal to
2 − r(x) + r'(y) − r(y) + r'(z)
The new rank of x is greater than the new rank of y, and the old rank of x is less than the old rank y, so this is at most
2 − r(x) + r'(x) − r(x) + r'(z) = 2 + r'(x) − 2r(x) + r'(z)
Now, let s(x) be the old size of x and let s'(x) be the new size of x. Consider the term 2r'(x) − r(x) − r'(z). This must be at least 2 because it is equal to lg(s'(x)/s(x)) + lg(s'(x)/s'(z)). Notice that this is the sum of two ratios where s'(x) is on top. Now, because s'(x) ≥ s(x) + s'(z), the way to make the sum of the two logarithms as small as possible is to choose s(x) = s(z) = s'(x)/2. But in this case the sum of the logs is 1 + 1 = 2. Therefore the term 2r'(x) − r(x) − r'(z) must be at least 2. Substituting it for the red 2 above, we see that the amortized time is at most
(2r'(x) − r(x) − r'(z)) + r'(x) − 2r(x) + r'(z) = 3(r'(x) − r(x))
as required.
Again, the amortized time is
2 + r'(x) − r(x) + r'(y) − r(y) + r'(z) − r(z)
Because the new rank of x is the same as the old rank of z, and the old rank of x is less than the old rank of y, this is
2 − r(x) + r'(y) − r(y) + r'(z)
≤ 2 − 2 r(x) + r'(y) + r'(z)
Now consider the term 2r'(x) − r'(y) − r'(z). By the same argument as before, this must be at least 2, so we can replace the constant 2 above while maintaining a bound on amortized time:
≤ (2r'(x) − r'(y) − r'(z)) − 2 r(x) + r'(y) + r'(z) = 2(r'(x) − r(x))
Therefore amortized run time in this case too is bounded by 3(r'(x) − r(x)), and this completes the proof of the amortized complexity of splay tree operations.