
Try to write concise, easy-to-read solutions - if you find yourself writing a lot of code you might not be pursuing the best solution. Think before you start coding! Save work where you can by using library functions.
You have the option to - and we recommend that you do - select a partner for this assignment. Only groups of at most two persons are permitted. You can register your group through CMS. Choose your partner carefully; it is not an acceptable excuse not to submit a finished homework because "the other partner did not work enough."
You can only modify the provided .sml files. Do not create new files. If needed, complete all function definitions with type specifications for both function arguments and function return types. Do not modify functions that we have provided for you. Do not modify the provided signature files or file sources.cm in any way.
Use the compilation manager to test your programs. Not only will compilation be simpler, but the error messages that you get will be more meaningful. To compile your code with the compilation manager switch to the directory that contains your files (including sources.cm), and type CM.make().
You might want to consider turning off garbage collection messages while developing your solutions to this assignment. You can achieve this by typing the line SMLofNJ.Internals.GC.messages false at the SML prompt.
In the writeup below we describe the functions that you have to implement, as well as the most important functions that we make available to you. The source we make available contains other functions as well; you should try to understand them enough so that, if needed, you can use them. Depending on the solution you chose, you might find that some of the functions we have provided are useful to you, or not. You are not obligated to make use of our functions, unless we explicitly tell you so. Remember, however, that you can not modify any of the functions we make available to you.
Non-compiling code will receive an automatic zero.
The game of NIM consists of an initial collection of n ≥ 1 piles of sticks. At each turn, each player can remove any number of sticks, as long as he removes at least one stick, but does not remove sticks from more than one pile. The player who must remove the last stick loses the game.
We encode the game's configuration as a list that contains n values, each of which represents the number of sticks left in a pile. Initially all values in the list must be positive (i.e. we do not allow for the initial existence of empty piles, and - obviously - for piles with negative numbers of sticks).
We identify players by numbers 1 and 2, respectively. We represent a move by the triple (player number, pile to remove stick from, number of sticks to remove); we number piles in order from the head of the list, starting at 0.
Consider the following initial configuration: [2, 4, 3]. If the first player executes move (1, 1, 4), then he removes all sticks from pile 1 (the second pile from the left in our list), to produce configuration [2, 0, 3]. Note that we allow empty piles after the initial configuration of the game.
One possible sequence of steps in a game starting in configuration [2, 4, 3] is the following (we show steps interspersed with the game configurations): [2, 4, 3] -> (1, 1, 2) -> [2, 2, 3] -> (2, 0, 2) -> [0, 2, 3] -> (1, 2, 1) -> [0, 2, 2] -> (2, 1, 2) -> [0, 0, 2] -> (1, 2, 1) -> [0, 0, 1] -> (2, 2, 1) -> [0, 0, 0]. The outcome of this particular sequence of moves is that player 2 loses the game.
The game of NIM has been studied, and its theory is well understood. Rather than relying on this theory, however, we will write a program that plays the game by simulating all possible outcomes of a given position, and by choosing a step that is guaranteed to be on the path to victory, if such step exists. The approach that we will adopt is called the min-max algorithm.
Given a configuration of a game, P0, we can represent the future evolution of the game with the help of a tree. The root of the tree consists of a node representing P0; the children of each intermediate node P are the nodes representing the legal configurations that can be generated from P.
Depending on the game that we are modeling, the tree representing its evolution can be finite or infinite. The tree of NIM is finite, because we have a finite number of sticks on the table, and at each step we remove at least one stick. It is possible for game trees to be infinite, for example, in games in which cyclical positions can arise.
For games with finite trees, it is possible - and common - for the same positions to arise in several parts of the tree, as an outcome of a difference sequence of steps. If the value of the current position or the set of possible future steps does not depend on the history of the game (i.e. on the steps that led to the current position), which is a common situation in positional games like chess or NIM, then certain parts of the game tree can be merged. The outcome of such a merger would be be DAG that allows for a more compact representation of the possible outcomes of the game. Further optimisations are possible for specific games. In the case of NIM, for example, it is possible to identify any two positions that are characterized by the same set of pile sizes, irrespective of their order. For example, configuration [a, b] can be identified with [b, a], since the possible future outcomes of these configurations are identical up to the permutation of piles. We will ignore all these possibilities for optimization in our problem, instead, we will work with the full tree.
We represent below the evolution of the game of NIM for the initial configuration [1, 2], assuming that player 1 is to move next:

Starting in this simple configuration the game ends in at least 2, and at most 3, steps. Player 1 has a winning strategy, which consists of removing the two sticks from the second pile, and thus forcing player 2 to remove the single stick left in the game.
NIM has a binary (or boolean) outcome: "win" or "lose." From the perspective of player 1 (the computer) we will associate a numerical value of 1 with a win, and a numerical value of 0 with a loss. We can use this convention to associate numerical values to each leaf node in the graph. Note that the configuration of each leaf node is identical for NIM; it is [0, 0]. For our game, the value of the final configuration is thus not determined by the configuration itself, but by the player on whose turn it arose. Note: we could take the view that a player confronted with the configuration [1, 0] loses; here we adopt the view that a player confronted with configuration [0, 0] wins.
The precise numerical values that we use are secondary, from the perspective of our problem all that matters is that a win is worth more than a loss, and that all wins are equivalent (and, of course, all losses are equivalent as well). There are games in which it is possible to win (or lose) in more than one way, case in which there would be several numerical values associated with the outcome of the game. In such situations, we would require that a better outcome (say, a more valuable win) be associated with a higher numerical value.
Let us adopt the point of view of player 1, while assuming that our adversary is a rational player who does not make mistakes. For us to win, we need to follow a path to the tree that connects the current position with a leaf node whose value is 1. The purpose of player 2 is to prevent us from following such a path, so that we end up in a leaf node with value 0. How can we achieve our goal?
Let us assume for a moment that we have a procedure that assigns numerical values to each node of the game tree, not only to leafs, and that the value of each node is 1 if player 1 can win the game, assuming that the given configuration arises, and 0 otherwise. Note that we did assume that this value assignment procedure refers only to nodes where player 1 is next to move.
Assume that we want to determine the value of a node in which player 1 is to play, and that all the children nodes have been evaluated already. The children node correspond to configurations in which player 2 is at play. Since player 2 is rational, player 2 must have chosen, from among all configurations that have been made available to him, the moves that have the worst possible outcome for player 1. Now, if player 1 chooses the node with the highest value from among the children of the current node, then player 1 is guaranteed to achieve this highest value (since the highest value is in fact the smallest value that a rational player 2 will let player 1 achieve on the path starting with the respective child node). Player 1 can make this choice, since it is his turn to move. A similar reasoning from the perspective of a node in which player 2 is to move concludes that player 2 - if he is a rational player - will always choose a child node that has the property that its value is the minimum value of all possible child nodes of the current node.
Our algorithm thus consists of two alternative "modes:" when we are in a node such that player 1 is to move, the value that will be assigned to the node will be the maximum value of the current node's children; when the current node is one in which player 2 is to move, the value assigned to the node is the minimum of the values associated with the current node's children. We note that we can label final configurations (leaf nodes) unambiguously, and that values in the tree percolate up to the root (i.e. we determine the values of nodes lower in the tree before we determine the values of node higher in the tree). Because of the alternation of the maximum and minimum choices at different levels in the tree, this algorithm is often referred to as the min-max algorithm.
In the graph above we have represented the values associated with all nodes of the game tree rooted at [2, 2]. The root ends up having value 1, which means that player 1 (the player that moves next) has a winning strategy. Player 1 performs the move that changes the current configuration into the configuration associated with the child node whose value is highest; in this case [1, 0].
It is possible for certain game trees not to have a path from the current configuration to a leaf node that is favorable (leads to a win), assuming that player 2 is rational. In such cases one could either give up the game, or select a random move, say, the move corresponding to the leftmost child node of the current node, and hope that player 2 will make a mistake. (Note: Assuming that it is possible for player 2 to make mistakes, we could do better than just select a random move, but we will not explore ths topic here.)
You will have to implement NIM in SML in the form of a game in which player 1 is a human using the keyboard, and player 2 is your program. To make your life easier, we have developed a lot of the infrastructure needed to play the game, which you can find in file nim.sml and games.sml:
We will represent game trees using the following type definition:
datatype 'a tree = Node of 'a * ('a tree list)
Strictly speaking, we do not need to define a datatype constructor Node, but we prefer to do it, to make the specification of tree datastructures more readable. To simplify things further, we did not make provisions for empty trees. Should the need for explicit representation of empty trees arise, this limitation can be easily corrected. Our tree datatype accommodates general trees, not only binary trees. By convention, we will refer to the first child in the list of children as the leftmost child.
Function printTree can be used to print a tree, assuming that a custom tree node printing function is provided.
(* NIM game configuration *)
type config = int list
(* NIM game tree *)
type game = config tree
(* Prints a node of a NIM game tree *)
fun printNimCfg(c: config, _: int): unit =
(print "[";
case c of
[] => raise Fail "can not happen"
| [e] => print (Int.toString e)
| h::tl => (print (Int.toString h);
map (fn e => print (", " ^ (Int.toString e))) tl;
());
print "]")
(* Prints a NIM game tree *)
val printGameTree = printTree printNimCfg
(* Builds a game tree starting in an initial configuration. *)
- val gt = makeGameTree [1, 2];
val gt =
Node
([1,2],
[Node ([0,2],[Node ([0,0],[]),Node ([0,1],[Node ([0,0],[])])]),
Node ([1,0],[Node ([0,0],[])]),
Node
([1,1],
[Node ([0,1],[Node ([0,0],[])]),Node ([1,0],[Node ([0,0],[])])])])
: game
- printGameTree gt;
[1, 2]
[1, 1]
[1, 0]
[0, 0]
[0, 1]
[0, 0]
[1, 0]
[0, 0]
[0, 2]
[0, 1]
[0, 0]
[0, 0]
You can best interpret the printout if you tilt your head to the left. Note that the left-most node at depth 1 is [0, 2], which is printed last of all nodes at that level, so that it appears left-most when you tilt your head to the left. Try to generate the tree that corresponds, say, to configuration [2, 2], and note how many nodes are repeated in the tree. Even though the game of NIM is simple, this redundancy makes the evaluation of big game trees challenging. As mentioned before, we could save some of the work by identifying configurations that are identical up to permutations of piles, for example, but we do not do that here. As a simple exercise, consider that you have a trivial initial configuration containing n piles of size 1, [1, 1, ..., 1]. Can you tell how many leaf nodes will our game tree have? If player 1 is to move, can you say who will win the game?
While this is not strictly necessary for the application of the min-max algorithm, for testability purposes we sort our configurations in increasing order at each level, so that the "smallest" configuration becomes the left-most child of the parent node, and the "biggest" configuration becomes the right-most child of the parent node. We define the ≤ operator on configurations with identical number of piles as follows: given c1=[n1, n2, ..., nk], and c2=[m1, m2, ..., mk], c1 ≤ c2 if and only if ni = mi for all i=1, 2, ..., r, 0 ≤ r ≤ k, and nr+1 ≤ mr+1 (we handle the case when r=0 and r=k in the obvious manner). Thus we have, for example, that [0, 2] ≤ [1, 0] ≤ [1, 1].
Function lessEqual, available as a stub in file nim.sml corresponds to the ≤ operator defined on NIM game configurations - you will have to implement it. We have provided stubs for functions greaterEqual and equalConfig, which determine whether, given configurations c1 and c2, we have c1 ≥ c2 or c1 = c2. You will have to implement these functions as well. Your functions should implement definitions for ≥ and = that are appropriate for the NIM game, and are logically consistent with the definition of operator ≤.
Given a configuration c, write function makeNextLevel whose declaration is as follows:
fun makeNextLevel(c: config): config list = ...
Assuming that the initial configuration is a legal one (all piles contain 0 or more entries), generate the list of successive steps, if any, and sort the resulting configurations in increasing order, based on the relation implemented by the lessEqual function.
Here are a few examples of how function makeNextLevel behaves:
- makeNextLevel []; val it = [] : config list - - makeNextLevel [0, 0, 0]; val it = [] : config list - - makeNextLevel [2]; val it = [[0],[1]] : config list - - makeNextLevel [1, 2]; val it = [[0,2],[1,0],[1,1]] : config list - - makeNextLevel [1, 2, 3]; val it = [[0,2,3],[1,0,3],[1,1,3],[1,2,0],[1,2,1],[1,2,2]] : config list
Implement function makeGameTree, which takes in a legal game configuration and produces the game tree rooted at the given configuration. A "legal game configuration" is one in which we have at least one pile, and all piles contain a non-negative number of sticks.
The declaration of makeGameTree is as follows:
fun makeGameTree (c: config): game = ...
Here is how the function works:
- makeGameTree [0, 0, 0];
val it = Node ([0,0,0],[]) : game
-
- makeGameTree [1];
val it = Node ([1],[Node ([0],[])]) : game
-
- makeGameTree [2];
val it = Node ([2],[Node ([0],[]),Node ([1],[Node ([0],[])])]) : game
-
- makeGameTree [1, 1];
val it =
Node ([1,1],[Node ([0,1],[Node ([0,0],[])]),Node ([1,0],[Node ([0,0],[])])])
: game
-
- makeGameTree [2, 2];
val it =
Node
([2,2],
[Node ([0,2],[Node ([0,0],[]),Node ([0,1],[Node ([0,0],[])])]),
Node
([1,2],
[Node ([0,2],[Node ([0,0],[]),Node ([0,1],[Node ([0,0],[])])]),
Node ([1,0],[Node ([0,0],[])]),
Node
([1,1],
[Node ([0,1],[Node ([0,0],[])]),
Node ([1,0],[Node ([0,0],[])])])]),
Node ([2,0],[Node ([0,0],[]),Node ([1,0],[Node ([0,0],[])])]),
Node
([2,1],
[Node ([0,1],[Node ([0,0],[])]),
Node
([1,1],
[Node ([0,1],[Node ([0,0],[])]),Node ([1,0],[Node ([0,0],[])])]),
Node ([2,0],[Node ([0,0],[]),Node ([1,0],[Node ([0,0],[])])])])])
: game
Given a game tree, we must assign values to its nodes. We achieve this with the help of function minMax, whose declaration is given below:
fun minMax (g: game, s: step): int tree = ...
This function applies the min-max algorithm to the game tree given as input, and returns the a tree of integers whose structure (but - obviously - not node values) is identical to the structure of the game tree given in the input. The s parameter can be either MIN or MAX, indicating whether we are evaluating the tree from the perspective of the maximizing player (the computer), or the minimizing player (the user sitting at the keyboard).
- minMax(makeGameTree [0, 0, 0], MAX);
val it = Node (1,[]) : int tree
-
- minMax(makeGameTree [1], MAX);
val it = Node (0,[Node (0,[])]) : int tree
-
- minMax(makeGameTree [1], MIN);
val it = Node (1,[Node (1,[])]) : int tree
-
- minMax(makeGameTree [2], MAX);
val it = Node (1,[Node (0,[]),Node (1,[Node (1,[])])]) : int tree
-
- minMax(makeGameTree [1, 1], MAX);
val it = Node (1,[Node (1,[Node (1,[])]),Node (1,[Node (1,[])])]) : int tree
-
- minMax(makeGameTree [2, 2], MAX);
val it =
Node
(0,
[Node (0,[Node (1,[]),Node (0,[Node (0,[])])]),
Node
(0,
[Node (1,[Node (0,[]),Node (1,[Node (1,[])])]),Node (0,[Node (0,[])]),
Node (1,[Node (1,[Node (1,[])]),Node (1,[Node (1,[])])])]),
Node (0,[Node (1,[]),Node (0,[Node (0,[])])]),
Node
(0,
[Node (0,[Node (0,[])]),
Node (1,[Node (1,[Node (1,[])]),Node (1,[Node (1,[])])]),
Node (1,[Node (0,[]),Node (1,[Node (1,[])])])])]) : int tree
-
- printTree (fn (n, _) => print (Int.toString n)) (minMax(makeGameTree [1,
2], MAX));
1
0
0
0
0
0
1
1
0
0
0
1
val it = () : unit
Note that the tree printed by the printTree function corresponds to the tree shown in the diagram above. Convince yourselves that it is so!
Write function chooseMove, which takes in the current game configuration and returns the value of the current node from the perspective of the maximizing player, and the next configuration to play. The next configuration to play is the leftmost child of the current node whose value is equal to the value of the current node, where the game tree is that which is generated by function makeGameTree. You can assume that the configuration provided to chooseMove is not a final configuration, i.e. that it contains at least a pile with at least one stick in it. We have provided a stub for function chooseMove, whose declaration is given below:
fun chooseMove (cfg: config): int * config = ...Here is how function chooseMove should behave:
- chooseMove [1]; val it = (0,[0]) : int * config - - chooseMove [2]; val it = (1,[1]) : int * config - - chooseMove [1, 2]; val it = (1,[1,0]) : int * config - - chooseMove [1, 1, 1]; val it = (0,[0,1,1]) : int * config - - chooseMove [2, 3, 4]; val it = (1,[2,3,1]) : int * config
We have provided a set of functions that can be used to play NIM interactively. We do not describe these functions in detail; it is part of your assignment to understand these functions well enough to use them.
After you compile the program using the compilation manager (CM.make()), you can type Nim.run() to play NIM interactively, or you can open the NIM structure and just issue the run() command. The game starts up in the default configuration [1, 2], for which you have a winning strategy (see the examples above). A new configuration is entered by typing in the number of sticks left in the pile after you made your move; the numbers are separated by commas. The program checks for the correctness of the moves that you enter. At any stage before one player wins, you can start a new game by typing in a new configuration preceded by the ":n " characters (no quotes). A new configuration can not have piles with no sticks.
Here are a few sample games:
- run(); --- CS312 NIM Game --- [1, 2] NIM >> 1,0 Your move: [1, 0] My move: [0, 0] I lost! val it = () : unit - - run(); --- CS312 NIM Game --- [1, 2] NIM >> :h Summary of commands: :n new game :h prints this help message :q terminates program execution If a line starts with a character other than ':', the text must describe a configuration. [1, 2] NIM >> :n 2,2,2 [2, 2, 2] NIM >> 1,2,2 Your move: [1, 2, 2] My move: [0, 2, 2] NIM >> 0, 3, 2 not a correct next step [0, 2, 2] NIM >> 0,2,1 Your move: [0, 2, 1] My move: [0, 0, 1] NIM >> 0,0,0 Your move: [0, 0, 0] You lost! val it = () : unit
What to submit: Do not modify any part of the Game structure. Modify only functions in file nim.sml whose definition is incomplete. These functions are: lessEqual, greaterEqual, equalConfig, makeNextLevel, makeGameTree, minMax, chooseMove. Submit the final version of file nim.sml through CMS.
We now turn our attention to another game, which we call Lolo. The game is played by two players on a board of 4-by-4 equal-sized squares. There are two L-shaped pieces in the game, each L-piece belonging to one player only. The L-shaped pieces cover 4 rectangles each. In addition, there are two square pieces that can be used by any of the players; they cover a single rectangle each. We show below the initial configuration of the game:
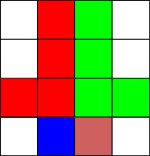
The green piece belongs to the computer, the red one belongs to the human player. The blue and brown pieces can be used by either player.
When a player's turn comes, he must lift his L-shaped piece from the board and put it back into a different position so that the piece is entirely on the board, but it does not cover any part of any other game piece. After the L-shaped piece has been placed on the board again, exactly one of the two square pieces must be moved to an empty square on the board. This completes the player's move. A player loses if he can not move his L-shaped piece to a new position when his turn comes.
If it is the human player's turn to move, one of the possible valid moves from the initial configuration is the one represented below:

To represent the state of the game, we need to develop a representation for the position of the various game pieces (from now on: pieces). We will, in fact, develop two representations (game state encondings).
The first encoding describes the exact location of a piece's component squares on the surface of the board. We describe these locations using four binary configurations of four bits each, where each bit represents a rectangle of the board. Bits bi0bi1bi2bi3 form binary configuration i=0,1,2,3; bit bij corresponds to row i, column j of the board (we start counting rows and columns from the top-left corner of the board; counting starts at 0). For simplicity, we will write binary configurations as decimal numbers.
The position of the red-colored L-piece in the initial configuration can then be represented as (0100, 0100, 1100, 0000) (or (4, 4, 12, 0) in decimal), that of the green L-shape as 0010, 0010, 0011, 0000 (decimal: (2, 2, 3, 0)), that of the blue piece as 0000, 0000, 0000, 0100 (decimal: (0, 0, 0, 4)), and that of the brown piece as 0000, 0000, 0000, 0010 (decimal: (0, 0, 0, 2)). To give one more example, the position of the red L-piece in the second diagram can be described by the decimal configuration (12, 8, 8, 0).
The encoding that we just defined allows us to represent the position of any piece using 4x4 bits, or four decimal numbers. These bits are not, however, independent. The encoding we chose would allow for a total of 216 values to be represented - we have many fewer valid configurations. This is a disadvantage that we will overcome by introducing a second encoding later. The binary encoding, however, is advantageous because it makes it easy to establish whether two (or more) pieces overlap by performing bit-by-bit logical operations between encodings.
0100 0000 0000 0100 bit-by-bit and 0010 = 0000 0110 0010 0010 0000 0110 0000
The two L-shapes whose binary configurations we have provided to the left of the equal sign overlap, as it can be seen on the configuration on the right. Note that the configuration on the right does not correspond to any piece; still, it is important because it shows that these two L-shapes can not simultaneously occupy the positions that their configurations imply. Note that overlaps can occur among any pair of distinct pieces from among the four pieces in play.
We have stated above that only a small subset of the possible value combinations that a binary configuration allows are actually used. If you examine file lolo.sml, you find the definitions of two Array2 datastructures, named lposarray (the array of all legal L-shape positions) and rposarray (the array of all legal positions for small squares). These arrays are filled with binary configuration data from lists lpositions and rpositions, respectively; one binary configuration is stored in one row of the arrays. The role of the arrays is to permit translations between abstract configurations, whereby the position of each piece is represented by a single decimal number (in fact, an index in an array of legal positions; the choice of array depends on the shape of the game piece at hand).
An abstract configuration of the game consists of a four-tuple (n0, n1, n2, n3), where n0 is the row index in lposarray that identifies the position of the red L-piece, n1 is the row index in lposarray that identifies the position of the green L-piece, n2 is the row index in dposarray that identifies the position of the blue square, while n3 is the row index in dposarray that identifies the position of the brown square. The initial configuration of the game is given by (0, 1, 0, 1), where - for example - the first 1 from the left indicates that the green L-piece is in a position that corresponds to row 1 (the second row; indices in SML are 0-based) of lposarray. This row contains the 4-tuple (2, 2, 3, 0), which corresponds to the binary configuration shown below:
0010 <---- 2 0010 <---- 2 0011 <---- 3 0000 <---- 0
In file lolo.sml the abstract configuration is represented by type config, while the binary configuration is represented by type bconfig. Remember that an abstract configuration expresses the configuration of all four pieces simultaneously using four numbers, while the binary configuration expresses the specific position of one piece on the board.
type bconfig = int * int * int * int type config = int * int * int * int
Function lookupPos, which is present in file lolo.sml only as a stub, converts the binary configuration that specifies the position of a single game piece into an index in the array of positions. The function declaration is given below:
fun lookupPos((p1, p2, p3, p4): bconfig, a: int Array2.array): int = ...
Array a is either lposarray or rposarray. If the binary configuration is not present in the given array, then the function raises an exception, specifically, it executes the line raise Fail "position not recognized".
Here is how the function works:
- lookupPos((4, 4, 12, 0), lposarray); val it = 0 : int - - lookupPos((0, 1, 7, 0), lposarray); val it = 39 : int - - lookupPos((15, 15, 15, 15), lposarray); uncaught exception Fail: position not recognized raised at: lolo.sml:105.18-105.48 - - lookupPos((0, 1, 0, 0), rposarray); val it = 6 : int uncaught exception Fail: position not recognized raised at: lolo.sml:105.18-105.48
You must implement function lookupPos.
We have provided helper functions that you can use to print and to read in game configurations. Functions cfg2str converts a game configuration to a string.
- cfg2str (0, 1, 0, 1); val it = ".12.\n.12.\n1122\n.34.\n" : string - - print(cfg2str (0, 1, 0, 1)); .12. .12. 1122 .34. val it = () : unit - - print(cfg2str (5, 10, 3, 7)); .232 .24. ..1. 111. val it = () : unit
This character representation uses digit '1' to represent the red L-piece, digit '2' to represent the green L-piece, digit '3' to represent the blue piece, digit '4' to represent the brown piece, and character '.' to explicitly show an unoccupied square. Note that the combination of characters '\n' represents the newline character. This becomes obvious when you print the strings returned by cfg2str. The last example above shows that cfg2str will not check whether the configuration it gets is legal or not. In this case the blue piece overlaps with the green piece.
Function str2cfg performs the opposite operation: it converts an input string into a game configuration. The input string must be entered on one line, using the same conventions as those of cfg2str, except that line separators will be indicated by the character '/' (slash). If the entered string does not encode a legal configuration, function str2cfg will raise an exception (raise Fail "position not recognized"). You can assume that no characters other than '1', '2', '3', '4', '.', and '/' will be used to describe a configuration.
- str2cfg "111./2.1./2224/..3."; val it = (6,43,1,10) : config - - str2cfg "42../.211/.221/3..1"; val it = (16,41,15,5) : config - - str2cfg "42../.211/.221/...1"; uncaught exception Fail: position not recognized raised at: lolo.sml:105.18-105.48 - - str2cfg "42.3/.211/.221/3..1"; uncaught exception Fail: position not recognized raised at: lolo.sml:105.18-105.48
You must implement function str2cfg.
Function checkConfig, when given an abstract configuration as an argument, establishes whether the respective abstract configuration is valid. We have provided this function for you.
- checkConfig (0, 1, 0, 1); val it = true : bool - - checkConfig (5, 5, 0, 1); val it = false : bool - - checkConfig (16,41,15,5); val it = true : bool - - checkConfig (1000, ~100, 100, ~1000); val it = false : bool
Function equalConfig, which we have also provided for you, compares two abstract configurations for equality.
- equalConfig ((0, 1, 0, 1), (0, 1, 0, 1)); val it = true : bool - - equalConfig ((0, 1, 0, 1), (1, 0, 0, 1)); val it = false : bool -
The game tree of Lolo is different from that of Nim. There are three essential differences that we need to analyze:
We note here that this heuristic does not guarantee that our program will win against a human player. If we play based on this heuristic, we are maximising the program's moves versus the number of moves available to the human player. The human player might have a harder time moving his L-piece (when compared to the program's larger number of options), but there is no guarantee that the program will actually win; it is possible that the configurations that allow for the most moves for the program are not those that allow no move for the human adversary.
Other heuristics could be defined, for example, one might want to define the valuation function as minus the number of steps available of the human (minimizing) player. We encourage you to experiment with alternative heuristics, but for the purposes of this problem we will stick with the original definition. The goal of winning the game is secondary for us; what we want to explore is how we can meaningfully play a game for which we do not know a definite winning strategy.
For example, in the initial position both the maximizing and the minimizing player have 48 distinct moves available, which are both derived from 4 possible positions each of the L-shaped pieces (the equality of new positions available to the players is unsurprising, since the initial position is symmetrical). The value of the position is then 0. Other positions are characterized by non-zero values, as shown below:
- countMoves((0, 1, 0, 1), MAX); val it = 4 : int - countMoves((0, 1, 0, 1), MIN); val it = 4 : int - evalPosition (0, 1, 0, 1); val it = 0 : int - - countMoves((16,41,15,5), MAX); val it = 7 : int - countMoves((16,41,15,5), MIN); val it = 3 : int - evalPosition (16,41,15,5); val it = 4 : int - print(cfg2str (16, 41, 15, 5)); 42.. .211 .221 3..1
You might be surprised by the large number of distinct steps available to a player in almost every configuration. You can understand this phenomenon better if you realize that for each new position of the L-piece you find, there will be 12 new game configurations that you can generate (there are 12 ways in which you can move a square once you moved your L-shaped piece). Hence the actual move counts will always be multiples of 12. Now we understand that 84 distinct moves are possible, for example, if there are 7 ways in which the maximising player can move his L-piece. Because of the constant ratio between the total number of distinct moves possible and the number of moves of the L-piece, our heuristic evaluation function evalPosition, as well as function countMoves, only consider (count) the distinct positions of the L-shaped piece.
Because the game trees are so big, we can not easily print or otherwise visualize them. Still, we have provided you with function printGameTree (see below). You can read these trees best if you tilt your head to the left - other than the fact that the printed game configuration is now a 4x4 array of characters, all the other details that we provided for Nim game tree printing are still valid.
While developing your solutions you might want to consider reducing the high branching factor of the game tree. If, for example, you temporarily eliminate entries from lists lpositions and rpositions, you can reduce the number of combinations that the program considers legal. This will allow you to examine a reduced version of the game and will make the size of the game tree manageable.
Functions countMoves and evalPosition rely on function nextLPos (see below). Given an input configuration, this function will produce the list of all possible configurations reachable from the current configuration, but only after moving the L-piece. If the second argument is MAX, then the moves are generated from the perspective of the maximing player (the computer, who plays with the green L-piece); if the second argument is MIN, then the moves are generated from the perspective of the minimizing player.
fun nextLPos((c1, c2, c3, c4): config, s: step): config list = ...
You will have to implement function nextLPos.
- nextLPos((31,38,5,1), MIN); val it = [] : config list - nextLPos((31,38,5,1), MAX); val it = [(31,41,5,1),(31,40,5,1),(31,39,5,1),(31,37,5,1),(31,36,5,1),(31,33,5,1), (31,32,5,1),(31,27,5,1),(31,23,5,1),(31,22,5,1),(31,16,5,1),(31,15,5,1), (31,13,5,1),(31,12,5,1),(31,11,5,1),(31,10,5,1),(31,1,5,1)] : config list - length(nextLPos((31,38,5,1), MAX)); val it = 17 : int
You must implement function nextLPos.
Function makeGameTree takes three arguments: the current game configuration, a level count, and a third parameter that specifies which player is to move. If the third parameter is MAX then we are first generating moves for the maximizing player (the computer); if the third parameter is MIN, then it is the minimizing player (the human player) whose moves will be generated first.
In the example below, the configuration we start in is a final one for the maximising player (this player loses, since he can not move), while the minimising player has several options available, as shown below. Note that the level count parameter is indicative only of the maximum number of levels that will be generated; if winning or losing configurations are reached earlier, then tree generation does not (and can not) go deeper. Remember that the level of a node is the number of edges from that node up to the root.
- str2cfg "223./21../21.4/.11."; val it = (35,24,3,10) : config - - printGameTree(makeGameTree (35,24,3,10) 10 MAX); 223. 21.. 21.4 .11. val it = () : unit - - printGameTree(makeGameTree (35,24,3,10) 1 MIN); 223. 21.. 21.4 .11. 22.3 2.1. 2.14 .11. 2234 2.1. 2.1. .11. 22.. 2.13 2.14 .11. 223. 2.14 2.1. .11. [intermediate nodes not shown] 223. 21.. 21.. 11.4
We have provided you with an implementation of makeGameTree. This implementation relies on function makeNextLevel, whose declaration is given below:
fun makeNextLevel((c1, c2, c3, c4): config, s: step): config list = ...
This function takes in an abstract game configuration and a value ("step") indicating whether we are generating moves on behalf of the maximising player (s=MAX), or the minimizing player (s=MIN). The function returns a list of all distinct configurations that the player whose moves we are emulating can reach in one step starting from the current configuration. As opposed to function nextLPos, this function generates full moves, i.e. it simulates the move of the L-piece followed by a move of one of the rectangular pieces.
Keep in mind that the two pieces that move move in sequence: first the L-piece moves, then one of the square pieces moves. This is important because the L-piece can not move to a position occupied before the move by the square that will ultimately be moved.
You will have to implement function makeNextLevel.
- makeNextLevel((31,38,5,1), MIN); val it = [] : config list - makeNextLevel((31,38,5,1), MAX); val it = [(31,1,5,14),(31,1,14,1),(31,1,5,12),(31,1,12,1),(31,1,5,8),(31,1,8,1), (31,1,5,6),(31,1,6,1),(31,1,5,4),(31,1,4,1),(31,1,5,2),(31,1,2,1), (31,10,5,14),(31,10,14,1),(31,10,5,12),(31,10,12,1),(31,10,5,11), ... some configurations deleted ... (31,41,5,7),(31,41,7,1),(31,41,5,6),(31,41,6,1),(31,41,5,3),(31,41,3,1), (31,41,5,2),(31,41,2,1)] : config list - length(makeNextLevel((31,38,5,1), MAX)); val it = 204 : int
Every time it is the computer's turn to move, we will generate the game tree up to a given depth. We can then assign a value to each leaf of the tree based on our heuristic function, then we can apply the min-max algorithm to determine the next step. Given how many moves are possible (remember that each new legal position of the moving player's L-piece leads to 12 distinct moves for that player), generating the game tree becomes difficult and resource-demanding even for relatively small values of the desired tree's depth. It would be great if we could find a way to either simplify the tree somehow, or if we could get away without exploring the tree fully. It turns out that a simple improvement on the min-max algorithm can reduce the number of nodes visited when determining the value of the current position. This optimized version of the min-max search is called the alpha-beta search.
In the alpha-beta search we associate two values with each node of the tree. The alpha value associated with a given node is the maximum score that can be achieved by the maximising player on any of the paths that have already been explored, and which pass through the current node or through one of the current node's ancestors in the current game tree. The beta value associated with a given node is the minimum score that can be achieved by the minimising player on any of the paths that have already been explored, and which pass through the current node or through one of the current node's ancestors in the current game tree. Note that from the perspective of the maximising player the alpha value is the best outcome the respective player can achieve, while from the perspective of the minimizing player the beta is also the best that the respective player can achieve.
Assume that the current node is characterized by values alpha0 and beta0, and that a new child node is explored whose associated value is v. If v < alpha0, then the respective child node will never be reached, because the maximising player would chose a more favorable route (the route that ends in a node valued alpha0). If If v > beta0, then the respective child node will not be reached, because the minimising player would chose a more favorable route (from the minimizing player's perspective) - the route that yields a value of beta0 for the minimizing player. Thus a child node should only be explored if its value is between alpha0 and beta0. If we ever have that beta0 ≤ alpha0, no further child node of the current node must be explored, as none of them will yield better paths than the best path already explored. We say that the respective child nodes (and their associated subtrees) have been pruned from the game tree.
Except for the pruned nodes, the values of the current node are computed as in the min-max algorithm. In addition, however, we need to update one of the alpha and beta values of the current node, depending on whether we perform a maximising or a minimising step, respectively. Alpha will be updated in the maximising step only if the value of the currently processed child node is greater than the current value of alpha; similarly, beta will be updated in the minimising step only if the value of the currently processed child node is less than the current value of beta.
Before any path is explored, the alpha node should be initialized to minus infinity (or the best possible approximation of it, the smallest possible integer), while the beta value should be initialized to plus infinity. Note that for a given node the alpha value can only increase, while the beta value can only decrease. The current values of alpha and beta must be passed to the child nodes of the current node, and must be updated at the level of the parent node after each child node has been processed.
Because Lolo game trees are so big, we will illustrate the behavior of the alpha-beta algorithm on a synthetic example shown below.

In the graph above we have represented the evolution of alpha, beta and that of the computed node value. We have greyed out the pruned nodes. The edge labels represent the order in which the respective edges are first visited. In this tree all leaf nodes are at the same depth; in general this is not the case.
When we developed a player for Nim we did generate the full game tree for each configuration that was current when the maximising player (the computer) was next to move. We did not stress this at that time, but this is clearly wasteful: to apply the min-max search we only need to keep around the current path to the root of the game tree - we can explore the tree piece by piece, without having to expend resources to generate it in its entirety. This idea is even more valid for the alpha-beta search, where - due to pruning - we don't even examine the entire tree.
Function alphaBeta has the following declaration:
fun alphaBeta (c: config) (depth: int) (s: step): int * config = ...
The first argument is the current configuration. Depth is the number of tree levels that will be generated, assuming that a winning or losing configuration is not reached; depth is always positive. The third argument indicates whether we should evaluate the current configuration from the perspective of the maximising player (s = MAX), or from the perspective of the minimising player (s = MIN). The function returns the value of the current configuration, and the configuration that describes the game after the optimal move has been executed.
- alphaBeta (35,24,3,10) 10 MAX; uncaught exception Fail: can not call alpha-beta with decided position raised at: lolo.sml:327.20-327.72 - - alphaBeta (35,24,3,10) 1 MIN; val it = (~1000,(38,24,3,0)) : int * config - - str2cfg ".322/1.2./1.2./114."; val it = (31,12,4,1) : config - - - alphaBeta (31,12,4,1) 3 MAX; val it = (1000,(31,38,5,1)) : int * config - - print(cfg2str (31,38,5,1)); 3... 1222 12.. 114. val it = () : unit
Function alphaBeta never keeps the entire game tree in memory; it implements the alpha-beta search as we described it above, including pruning.
You will have to implement function alphaBeta.
After you complete all your functions, compile your program using the compilation manager. You can then type Lolo.run(), or open Lolo followed by run(). Type ":h" (no quotes) at the game prompt to see a list of available commands. Any command can be issued at any time.
We show below a sample game of Lolo. Note how quickly the human user loses when the game is played at level 3. The default game level is 2; you can modify this any time during a game.
Unless you have a very fast computer with a lot of memory, you will probably find that game levels 1, 2, or 3 are the ones that you can explore thoroughly - higher game levels take a long time to generate the next step. You can, however, explore higher levels if you temporarily remove some entries from the lpositions and rpositions lists. The branching factor will decrease, as some otherwise legal positions will not be accessible to the program anymore.
- run(); --- CS312 Lolo Game --- .12. .12. 1122 .34. Lolo >> :l 3 .12. .12. 1122 .34. Lolo >> 132./1.2./1122/..4. Your move: 132. 1.2. 1122 ..4. My move: 1.22 132. 112. ..4. Lolo >> .322/1.2./1.2./114. Your move: .322 1.2. 1.2. 114. My move: 3... 1222 12.. 114. I win! val it = () : unit
What to submit: Do not modify any part of the Game structure. Modify only functions in file lolo.sml whose definition is incomplete. These functions are: lookupPos, str2cfg, nextLPos, makeNextLevel, and alphaBeta. Submit the final version of file lolo.sml through CMS.
Acknowledgement: The author of this writeup wishes to thank Adrian Nistor for introducing him to the game of Lolo many years ago.