CS312 PROBLEM SET 5A
Issued: Monday, November 3
Due: Friday, December 5
This problem set will have two parts. The second part will be release in approximately one week. You will hand in both parts at once, as a single problem set.
You have longer to do this problem set than you did on previous problem sets. This is not an accident; this problem set is significantly more work. So get started early!
You may do this problem set alone or in pairs. You will submit the files you changed through CMS.
More Sophisticated Program Analysis
In this problem set you will explore two much more sophisticated forms of program analysis than you did in PS#4. The basic data structures used (namely, AST�s) will remain the same; however, the analysis will be much more sophisticated, and provide an opportunity to explore interesting algorithms and data structures.
We have provided you with a main loop for your analysis routines, much like the optimization main loop in PS#4.
Test cases for this problem set
In order to minimize the ambiguities in this problem set, we have provided a set of examples showing how your code should behave. These examples have actually been run using our solutions. If there is sufficient demand we will add additional examples over time.
Call Graphs
The first task that we will consider in this problem set centers on the notion of a call graph. Recall that a graph is a set of vertices (sometimes called nodes) connected by edges. The graph that we will consider involves directed edges, which means that we consider the edge that goes from v1 to v2 to be different from the edge that goes from v2 to v1.
In a call graph, the vertices represent functions. There is an edge from (the vertex representing) function1 to (the vertex representing) function2 when the function1 calls function2. For example, consider the SML expression:
let fun ford(x) = x-20 fun arthur(y) = ford(y)*10 fun marvin(z) = arthur(z)+2in marvin(24)end
This expression has the following call graph:
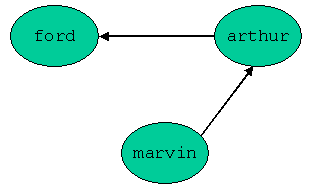
Note that there is no edge from marvin to ford, because marvin does not
call ford (at least, not
directly).
Furthermore, the expression above only calls
one function directly, namely marvin. In contrast, the expression below also calls ford
directly.
let fun ford(x) = x-20 fun arthur(y) = ford(y)*10 fun marvin(z) = arthur(z)+2in marvin(ford 44)end
In order to construct a call graph, we need
to specify what it means to say that a function f calls a function g. Ideally, we would say that f calls g
if at runtime f will invoke the
procedure g. This, however,
is clearly uncomputable, as shown from the following example:
fun f(x) = if (ford(x) = 42) then g(x) else 6*9
In order to figure out if f is actually going to call g we need to know the value of x, which we only know at runtime. Furthermore,
determining the return value of some arbitrary function like ford
is well known to be uncomputable.
As a result, we will use a sound (but
conservative) compromise: when we say that f calls g,
what we will mean is that f
could potentially call g
directly. To put it another way, this means that we cannot prove that f will not directly call g at run time. This definition is sound, in that if f
actually calls g at run time, then under our definition we say that f calls g.
It is conservative, because it is possible for us to say that f calls g when
at run time f decides not in fact
to call g. The advantage
of this definition is that it is easy to compute: we simply test if the
identifier g appears anywhere inside the body of the definition of
f.
Simplifying assumptions
In order to make this problem considerably easier, you can make the
following assumptions about the input expression that you will optimize:
Alpha renaming: In your solutions, you can assume that alpha renaming has already occurred (i.e. that any two identifiers with the same name are in fact the same).
Limited input expressions: You can assume that your input expression is in the same
form as the two let
expression examples given above. More
precisely, the input expression is a let
expression containing fun declarations (no
val
declarations), and there are no other let or fn expressions anywhere within the input expression.
Simple syntax for mutual
recursion: To define mutually
recursive functions in SML it is necessary to use the keyword and
(not to be confused with andalso). However,
in order to simplify this problem set we will assume that functions defined
with fun in a let can be
mutually recursive.
Thus, for example, your code
should handle the following mutually recursive pair of functions:
let
fun take(L:int list):int list =
if L = nil then nil else hd(L)::skip(tl(L))
fun skip(L:int list):int list =
if L=nil then nil else take(tl(L));
in
take [1,2,3]
end
In order for this to work in
SML, the second fun (shown in bold) would need to
be replaced by and.
What to hand in:
In this problem set, you will modify the included file callgraphs.sml. This is the only file you should modify.
Call graph problem 1: dead code elimination
The first call graph problem involves detecting
and eliminating dead code. More precisely, there can be functions that are
declared that are not used in the body. As a simple example, consider:
let fun ford(x:int):int = x-20 fun arthur(y:int):int = (y-20)*10 fun marvin(z:int):int = arthur(z)+2in marvin(24)end
In this expression, the function ford is never called. Obviously, it would be desirable to
detect such �dead� functions (and perhaps rewrite the code to remove them).
In this problem you are to detect and remove
dead functions. The two procedures that you need to write are listDeadFunctions and removeDeadFunctions. Their signatures are provided in callgraphs.sml, and
the analyzer will call them and report on their results. Note that the
input will only be expressions in the restricted form that we use for call
graph analysis. Be sure that your code works correctly for recursive functions.
Problem CG-1.1: Write a function listDeadFunctions which
takes an expression and returns a list of strings, which are the names of the
dead functions.
Problem CG-1.2: Write a function removeDeadFunctions which
takes an expression and returns a new expression, which has removed the dead
functions.
Call graph problem 2: recursive function detection
Recursive functions, and especially
mutually recursive functions, cause a fair amount of complexity. For example,
it is not possible to inline such functions. In this problem, you will detect
recursive functions. Note that in this definition, we consider not only the
functions that f calls directly, but also that it calls indirectly. For
example, if f calls g, which in turn calls f, then f is recursive.
To handle this, we need a
definition of what it means for a function to be recursive. In classic CS312
fashion, this definition (of course!) will be recursive.
More precisely, we define a
function f to be recursive if f is in callable(f), where:
- g is in callable(f) if g appears in the body of
f
- g is in callable(f) if there exists some
function h in callable(f) such that g appears in the body of h
Problem CG-2: Write a function listRecursiveFunctions which
takes an expression and returns a list of strings. Each element of the output
will a function which calls itself, either directly or indirectly. Note that
the input will only be expressions in the restricted form that we use for call
graph analysis.
Call graph problem 3: detecting functions that cause side effects
Functions which cause side effects are even more difficult to optimize than recursive functions. Not only are they impossible to inline, but they are extremely difficult to reason about. For this reason, we will attempt to detect such functions.
As usual, we have the problem that it is uncomputable to tell whether or not a function will actually cause a side effect at run time. However, there is a simple syntactic test we can do, which is sound but conservative. If a function ever uses the assignment operator :=, then we will assume that it causes side effects.
In this problem, your task is to detect all functions that cause side effects, either directly (by using the assignment operator) or indirectly, by calling some other function which causes side effects.
Problem CG-3: Write a function listImperativeFunctions which takes an expression and returns a list of the names of functions which could cause side effects. Note that the input will only be expressions in the restricted form that we use for call graph analysis.