# Abstraction Functions and Representation Invariants * * * <i> Topics: * module specifications * abstraction functions * representation invariants </i> * * * ## Module specifications Let us now consider the use of specification in module *implementations*. The first question we must ask ourselves is who is going to read the comments written in module implementations. Because we are going to work hard to allow module clients to program against the module while reading only its interface, clearly clients are not the intended audience. Rather, the purpose of implementation comments is to explain the implementation to other implementers or maintainers of the module. This is done by writing comments that convince the reader that the implementation correctly implements its interface. It is inappropriate to copy the specifications of functions found in the module interface into the module implementation. Copying runs the risk of introducing inconsistency as the program evolves, because programmers don't keep the copies in sync. Copying code and specifications is a major source (if not *the* major source) of program bugs. In any case, implementers can always look at the interface for the specification. Implementation comments fall into two categories. The first category arises because a module implementation may define new types and functions that are purely internal to the module. If their significance is not obvious, these types and functions should be documented in much the same style that we have suggested for documenting interfaces. Often, as the code is written, it becomes apparent that the new types and functions defined in the module form an internal data abstraction or at least a collection of functionality that makes sense as a module in its own right. This is a signal that the internal data abstraction might be moved to a separate module and manipulated only through its operations. The second category of implementation comments is associated with the use of *data abstraction*. Suppose we are implementing an abstraction for a set of items of type `'a`. The interface might look something like this: ``` (* A set is an unordered collection in which multiplicity is ignored. *) module type Set = sig (* the type representing a set whose elements are type ['a] *) type 'a set (* the set containing no elements *) val empty : 'a set (* [mem x s] is whether [x] is a member of set [s] *) val mem : 'a -> 'a set -> bool (* [add x s] is the set containing all the elements of [s] * as well as [x]. *) val add : 'a -> 'a set -> 'a set (* [rem x s] is the set containing all the elements of [s], * minus [x]. *) val rem : 'a -> 'a set -> 'a set (* [size s] is the cardinality of [s] *) val size: 'a set -> int (* [union s1 s2] is the set containing all the elements that * are in either [s1] or [s2]. *) val union: 'a set -> 'a set -> 'a set (* [inter s1 s2] is the set containing all the elements that * are in both [s1] and [s2]. *) val inter: 'a set -> 'a set -> 'a set end ``` In a real signature for sets, we'd want operations such as `map` and `fold` as well, but let's omit these for now for simplicity. There are many ways to implement this abstraction. One easy way is as a list: ``` (* Implementation of sets as lists with duplicates *) module ListSetDups : Set = struct type 'a set = 'a list let empty = [] let mem = List.mem let add x l = x :: l let rem x = List.filter ((<>) x) let rec size = function | [] -> 0 | h :: t -> size t + (if mem h t then 0 else 1) let union l1 l2 = l1 @ l2 let inter l1 l2 = List.filter (fun h -> mem h l2) l1 end ``` This implementation has the advantage of simplicity. For small sets that tend not to have duplicate elements, it will be a fine choice. Its performance will be poor for large sets or applications with many duplicates but for some applications that's not an issue. Notice that the types of the functions do not need to be written down in the implementation. They aren't needed because they're already present in the signature, just like the specifications that are also in the signature don't need to be replicated in the structure. Here is another implementation of `Set` that also uses `'a list` but requires the lists to contain no duplicates. This implementation is also correct (and also slow for large sets). Notice that we are using the same representation type, yet some important aspects of the implementation are quite different. ``` (* Implementation of sets as lists without duplicates *) module ListSetNoDups : Set = struct type 'a set = 'a list let empty = [] let mem = List.mem (* add checks if already a member *) let add x l = if mem x l then l else x :: l let rem x = List.filter ((<>) x) let size = List.length (* size is just length if no duplicates *) let union l1 l2 = (* check if already in other set *) List.fold_left (fun a x -> if mem x l2 then a else x :: a) l2 l1 let inter l1 l2 = List.filter (fun h -> mem h l2) l1 end ``` An important reason why we introduced the writing of function specifications was to enable *local reasoning*: once a function has a spec, we can judge whether the function does what it is supposed to without looking at the rest of the program. We can also judge whether the rest of the program works without looking at the code of the function. However, we cannot reason locally about the individual functions in the three module implementations just given. The problem is that we don't have enough information about the relationship between the concrete type (`int list`) and the corresponding abstract type (`set`). This lack of information can be addressed by adding two new kinds of comments to the implementation: the *abstraction function* and the *representation invariant* for the abstract data type. ## Abstraction functions The client of any `Set` implementation should not be able to distinguish it from any other implementation based on its functional behavior. As far as the client can tell, the operations act like operations on the mathematical ideal of a set. In the first implementation, the lists `[3; 1]`, `[1; 3]`, and `[1; 1; 3]` are distinguishable to the implementer, but not to the client. To the client, they all represent the abstract set {1, 3} and cannot be distinguished by any of the operations of the `Set` signature. From the point of view of the client, the abstract data type describes a set of abstract values and associated operations. The implementers knows that these abstract values are represented by concrete values that may contain additional information invisible from the client's view. This loss of information is described by the *abstraction function*, which is a mapping from the space of concrete values to the abstract space. 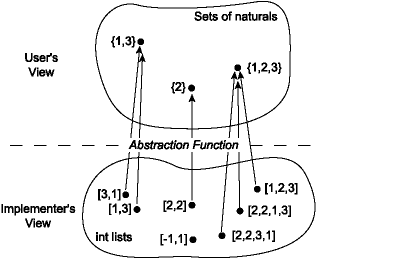The abstraction function for the implementation `ListSetDups` looks like this:  Notice that several concrete values may map to a single abstract value; that is, the abstraction function may be *many-to-one*. It is also possible that some concrete values do not map to any abstract value; the abstraction function may be *partial*. That is not the case with `ListSetDups`, but it might be with other implementations. The abstraction function is important for deciding whether an implementation is correct, therefore it belongs as a comment in the implementation of any abstract data type. For example, in the `ListSetDups` module, we could document the abstraction function as follows: ``` module ListSetDups : Set = struct (* Abstraction function: the list [a1; ...; an] represents the * smallest set containing all the elements a1, ..., an. * The list may contain duplicates. * [] represents the empty set. *) type 'a set = 'a list ... ``` This comment explicitly points out that the list may contain duplicates, which is helpful as a reinforcement of the first sentence. Similarly, the case of an empty list is mentioned explicitly for clarity, although it is redundant. The abstraction function for the second implementation, which does not allow duplicates, hints at an important difference: we can write the abstraction function for this second representation a bit more simply because we know that the elements are distinct. ``` module ListSetNoDups : Set = struct (* Abstraction function: the list [a1; ...; an] represents the set * {a1, ..., an}. [] represents the empty set. *) type 'a set = 'a list ... ``` ## Commutative diagrams Using the abstraction function, we can now talk about what it means for an implementation of an abstraction to be *correct*. It is correct exactly when every operation that takes place in the concrete space makes sense when mapped by the abstraction function into the abstract space. 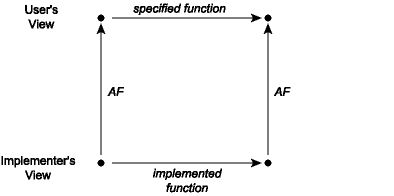This can be visualized as a *commutative diagram*:  A commutative diagram means that if we take the two paths around the diagram, we have to get to the same place. Suppose that we start from a concrete value and apply the actual implementation of some operation to it to obtain a new concrete value or values. When viewed abstractly, a concrete result should be an abstract value that is a possible result of applying the function *as described in its specification* to the abstract view of the actual inputs. For example, consider the union function from the implementation of sets as lists with repeated elements covered last time. When this function is applied to the concrete pair [1; 3], [2; 2], it corresponds to the lower-left corner of the diagram. The result of this operation is the list [2; 2; 1; 3], whose corresponding abstract value is the list {1, 2, 3}. Note that if we apply the abstraction function AF to the input lists [1; 3] and [2; 2], we have the sets {1, 3} and {2}. The commutative diagram requires that in this instance the union of {1, 3} and {2} is {1, 2, 3}, which is of course true. ## Representation invariants The abstraction function explains how information within the module is viewed abstractly by module clients. However, this is not all we need to know to ensure correctness of the implementation. Consider the `size` function in each of the two implementations. For `ListSetNoDups`, in which the lists of integers have no duplicates, the size is just the length of the list: ``` let size = List.length ``` But for `ListSetDups`, which allows duplicates, we need to be sure not to double-count duplicate elements: ``` let rec size = function | [] -> 0 | h :: t -> size t + (if mem h t then 0 else 1) ``` How we know that we don't need to do this check in `ListSetNoDups`? Since the code does not explicitly say that there are no duplicates, implementers will not be able to reason locally about whether functions like `size` are implemented correctly. The issue here is that in the `ListSetNoDups` representation, not all concrete data items represent abstract data items. That is, the *domain* of the abstraction function does not include all possible lists. There are some lists, such as `[1; 1; 2]`, that contain duplicates and must never occur in the representation of a set in the `ListSetNoDups` implementation; the abstraction function is undefined on such lists. We need to include a second piece of information, the *representation invariant* (or *rep invariant*, or *RI*), to determine which concrete data items are valid representations of abstract data items. For sets represented as lists without duplicates, we write this as part of the comment together with the abstraction function: ``` module ListSetNoDups : Set = struct (* Abstraction function: the list [a1; ...; an] represents the set * {a1, ..., an}. [] represents the empty set. * * Representation invariant: the list contains no duplicates. *) type 'a set = 'a list ... ``` If we think about this issue in terms of the commutative diagram, we see that there is a crucial property that is necessary to ensure correctness: namely, that all concrete operations preserve the representation invariant. If this constraint is broken, functions such as `size` will not return the correct answer. 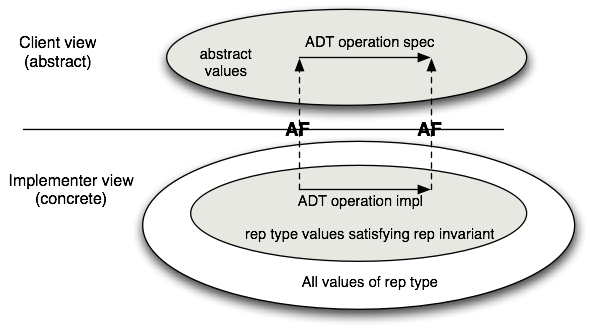The relationship between the representation invariant and the abstraction function is depicted in this figure:  We can use the rep invariant and abstraction function to judge whether the implementation of a single operation is correct *in isolation from the rest of the module*. It is correct if, assuming that: 1. the function's preconditions hold of the argument values 2. the concrete representations of the arguments satisfy the rep invariant we can show that 1. all new representation values created satisfy the rep invariant, and 2. the commutative diagram holds. The rep invariant makes it easier to write code that is provably correct, because it means that we don't have to write code that works for all possible incoming concrete representations&mdash;only those that satisfy the rep invariant. For example, in the implementation `ListSetNoDups`, we do not care what the code does on lists that contain duplicate elements. However, we do need to be concerned that on return, we only produce values that satisfy the rep invariant. As suggested in the figure above, if the rep invariant holds for the input values, then it should hold for the output values, which is why we call it an *invariant*. ## Implementing the rep invariant When implementing a complex abstract data type, it is often helpful to write an internal function that can be used to check that the rep invariant holds of a given data item. By convention we will call this function `rep_ok`. If the module accepts values of the abstract type that are created outside the module, say by exposing the implementation of the type in the signature, then `rep_ok` should be applied to these to ensure the representation invariant is satisfied. In addition, if the implementation creates any new values of the abstract type, `rep_ok` can be applied to them as a sanity check. With this approach, bugs are caught early, and a bug in one function is less likely to create the appearance of a bug in another. A convenient way to write `rep_ok` is to make it an identity function that just returns the input value if the rep invariant holds and raises an exception if it fails. ``` (* Checks whether x satisfies the representation invariant. *) let rep_ok (x : int list) : int list = ... ``` Here is an implementation of `Set` that uses the same data representation as `ListSetNoDups`, but includes copious `rep_ok` checks. Note that `rep_ok` is applied to all input sets and to any set that is ever created. This ensures that if a bad set representation is created, it will be detected immediately. In case we somehow missed a check on creation, we also apply `rep_ok` to incoming set arguments. If there is a bug, these checks will help us quickly figure out where the rep invariant is being broken. ``` (* Implementation of sets as lists without duplicates. * Includes rep_ok checks. *) module ListSetNoDupsRepOk : Set = struct (* Abstraction function: the list [a1; ...; an] represents the * set {a1, ..., an}. [] represents the empty set {}. * * Representation invariant: the list contains no duplicates. *) type 'a set = 'a list let rep_ok (l : 'a set) : 'a set = List.fold_right (fun x t -> assert (not (List.mem x t)); x :: t) l [] let empty = [] let mem x l = List.mem x (rep_ok l) let add x l = rep_ok (if mem x (rep_ok l) then l else x :: l) let rem x l = rep_ok (List.filter ((<>) x) (rep_ok l)) let size l = List.length (rep_ok l) let union l1 l2 = rep_ok (List.fold_left (fun a x -> if mem x l2 then a else x :: a) (rep_ok l2) (rep_ok l1)) let inter l1 l2 = rep_ok (List.filter (fun h -> mem h l2) (rep_ok l1)) end ``` Calling `rep_ok` on every argument can be too expensive for the production version of a program. The `rep_ok` above is quite expensive (though it could be implemented more cheaply). For production code, it may be more appropriate to use a version of `rep_ok` that only checks the parts of the rep invariant that are cheap to check. When there is a requirement that there be no run-time cost, `rep_ok` can be changed to an identity function (or macro) so the compiler optimizes away the calls to it. However, it is a good idea to keep around the full code of `rep_ok` (perhaps in a comment) so it can be easily reinstated during future debugging. Some languages provide support for conditional compilation. These constructs are ideal for checking representation invariants and other types of sanity checks. There is a compiler option that allows such assertions to be turned on during development and turned off for the final production version. For example, the ocaml compiler supports a flag `noassert` that disables assertion checking. ## Terms and concepts * abstract value * abstraction function * commutative diagram * conditional compilation * concrete value * data abstraction * many to one * partial * rep ok * representation invariant * representation type ## Further reading * [*Program Development in Java: Abstraction, Specification, and Object-Oriented Design*][liskov-guttag], chapter 5, by Barbara Liskov with John Guttag. [liskov-guttag]: https://newcatalog.library.cornell.edu/catalog/9494027