CS212 Problem Sets
Problem Set 1 - Spring 1999
Fractals

Issued: Tuesday, February 2
Due: Tuesday, February 9

The von Koch Snowflake
Programming Assignments

Before you do anything, please read about the entire homework carefully. It contains a wealth of good advice that can save you (and us) a lot of headaches later on.

For this assignment, you are to work alone. Turn in your code using the email system, as you should know by now. Once the due date is over, no more works will be accepted. No late assignments will be accepted, so start early. (In case of an exceptional situation, mail the course staff.)

For this exercise is to work you should leave the language configured to the default "R4RS+" mode.

If you have trouble with the course software or are generally stuck, come to our office hours or consulting hours. Alternatively, post a question to the newsgroup cornell.class.cs212. As a last resort, send email to cs212@cs.cornell.edu.

The von Koch Snowflake

In this problem set, you will be experimenting with fractals. Among the most famous fractals are the von Koch snowflake, first described by Helge von Koch in 1904, the Peano curve, the Hilbert curve, and the Cantor set. These figures not only look pretty, but also have important applications in many fields. For example, the Hilbert curve is used in dithering and compressing images.

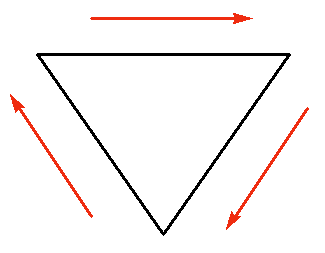
Many fractals can be specified by giving an initiator and a generator. The initiator is a starting shape, and the generator is a rule that can be applied to refine the shape. We can think of the initiator as a very rough initial approximation to the fractal. We can start with the initiator, then apply the generator as many times as we like to achieve better and better approximations. For the von Koch snowflake, the initiator is an equilateral triangle with sides oriented in a clockwise direction. (The red arrows show the direction of orientation only; they are not part of the figure.)

The generator of the von Koch snowflake is a rule that says: for any (oriented) line segment, remove the middle third and replace it by two sides of an equilateral triangle. The two new segments should extend to the left of the original segment when facing in the direction of orientation. That is, replace the oriented segment

by the four segments

oriented as shown.

To generate the fractal corresponding to a given initiator and generator, we conceptually generate a sequence of figures, each figure more refined than the last. The first figure is the initiator. The i+1^st figure is obtained by applying the generator to each oriented line segment in the i^th figure. For the von Koch snowflake, the first figure would be the equilateral triangle, the second would be a six-pointed star, the third would be a six-pointed star with little bumps on each point, etc.

The fractal itself is the limit of these approximations. Fractals have a number of fascinating mathematical properties. They are self-similar, which means roughly that no matter how much you zoom in, the object still looks the same. They are continuous but nowhere differentiable. Their length is either 0 or infinite. One can define the dimension of a fractal in a natural way, and it turns out that their dimension is not 1 like curves or 2 like surfaces, but somewhere in between, which is why they are called fractals. The dimension of the von Koch snowflake is log 4/log 3 = 1.2618...

In this assignment you will construct level k approximations to fractals. These are the figures obtained by stopping the construction described above after stage k. For example, a level 0 von Koch snowflake consists of just an equilateral triangle; a level 1 von Koch snowflake is the six-pointed star; etc.

These figures can be created without having to actually generate the intermediate figures by using a recursive strategy for drawing a side of the figure. A level 0 side is just a straight line. A level k+1 side is made up of several level k sides. In the von Koch snowflake, a level k+1 side consists of four level k sides.

We can translate this strategy into a Scheme procedure that draws a side of a given level (specified by the parameter level) and of a given length (specified by the parameter length) using the current direction and from the current position, both specified the "turtles" package. If the level is 0, we simply draw a straight line of the given length. If the level is greater than 0, we recursively draw four sides of level level-1 and length length/3 in the appropriate directions relative to the initial angle.

(define (side length level)
  (if (<= level 0)
    (draw length)
    (begin
      (side (/ length 3) (- level 1))
      (turn -60)
      (side (/ length 3) (- level 1))
      (turn 120)
      (side (/ length 3) (- level 1))
      (turn -60)
      (side (/ length 3) (- level 1)))))

The procedure draw draws a line segment by moving a graphic "turtle" using its current angle and the given distance.

We can draw the level k snowflake by drawing three level k sides oriented at 0 radians, 2pi/3 radians, and -2pi/3 radians, where pi = 3.14159...

(define (snowflake length level)
  (turn 90)
  (move (- (/ length 2)))
  (turn -30)
  (side length (- level 1))
  (turn 120)
  (side length (- level 1))
  (turn 120)
  (side length (- level 1))
  (turn 120)
  (turn 30)
  (move (/ length 2))
  (turn -90))

The file ps1.ss contains these two functions, you can open them to chek their contents (in collects/DrSwindle/lib). Do not try to use load or to click "Execute" when this file is opened - it won't work. To use this, set the library to this file using the language menu (as shown in class) and click then click "Execute". You will be writing code which is based on this file.

Once you have loaded this file, you can test the program by initializing the turtle package by evaluating (turtles #t) and then enter the expression:

(snowflake 100 4)

to draw a level 3 snowflake of side-length 100.

You can look at the DrScheme manual to learn about the available turtle functions, for example, using the clear function to erase the window.

Remember not to try using the main window when the mouse pointer hovers over the turtle-graphics window.

Problem 1: Different Initiators and Generators

The snowflake figure is just one of a large family of figures that can be drawn using the same general function. Changing the generator and/or the initiator can completely change the shape of the figure.

Write a new generator function (flip-side length level) in which the first half of the oriented line segment is replaced with the two equal sides of an isosceles right triangle extending to the left and the last half with the two equal sides of an isoceles right triangle extending to the right.

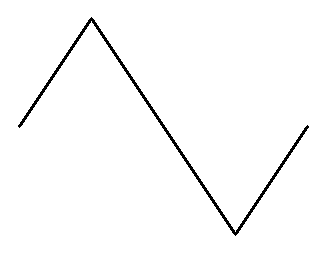
It should be considered as 4 segments of equal length, not 3 segments.

Write a new initiator function square-snowflake that is a square and uses flip-side as a generator. Try out your new initiator and see what kind of image it generates.

What to turn in: For problem 1, please submit the new functions flip-side and square-snowflake.

Notes:

You can add the expression (turtles #t) at the bottom of the definitions window, so whenever you click the execute button, you'll get the window to come up (it will disappear on every environment reset).
Another thing that will make your life a bit simpler is adding a definition that will serve as a testing shortcut, something like (define (test n) (square-snowflake 200 n)).
Remember to comment your functions, and add "separator" lines between functions that belong to different exercises.
You might want to have some code that will get the turtle to start from a corner point so you will be able to use bigger shapes. Make sure that you comment such initialization code properly.

Problem 2: Generalizing the Line System

Principle: Functional abstraction, functions as parameters.

Using the initiator given to you and in the initiator you wrote, the shape of the generator is "hard-coded". But it makes perfect sense to define line systems using any combination of generator and initiator. For instance, we should be able to use the square initiator with the original von Koch generator. What we need is some general way to glue together a generator and initiator so that we can try out different combinations.

One idea is to parameterize the initiator by the generator. That is, we could modify initiators so that they take the generator as an argument.

Write two new functions, snowflake-1 and square-snowflake-1 based on snowflake and square-snowflake so that they take a generator function as an argument and invoke this generator instead of a hardcoded one. Try out all four combinations of initiators and generators:

(snowflake-1 200 4 side)
(snowflake-1 200 4 flip-side)
(square-snowflake-1 200 4 side)
(square-snowflake-1 200 4 flip-side)

In particular, evaluating the first expression should yield the same figure as the original snowflake code.

What to turn in: For problem 2, please submit a listing of the two new procedures snowflake-1 and square-snowflake-1.

Problem 3: Inverting the Generator

Principle: Functions as parameters.

There is no reason why the generators should stay the same all the time, even in the same figure. Interesting designs can be obtained by inverting the generator on some levels.

We can easily invert an arbitrary generator by changing the signs of the angles that we add to the original heading. The decision whether to use a regular or inverted generator could be a function of the level; for example, we might decide to invert the generator on odd levels and not to invert on even levels. Alternatively, we might decide to invert on every third level, or we might decide to never invert at all.

To support an arbitrary inversion strategy, we need to pass a procedure inverter to the initiator which then forwards inverter to the generator. The generator should call the inverter, passing in the current level, to determine the sign of the angle to add to the original heading. The inverter procedure should return either the +(plus) or -(subtract) functions that will be used as a unary operator..

Implement the changes indicated above by adding function inverter to the parameter list of snowflake and side, rewriting them as snowflake-2 and side-2 (don't forget to modify the functions called by these functions as well). To test your code, evaluate:

(snowflake-2 200 4 (lambda (level) +))

and verify that you obtain the original snowflake figure as before.

You can also examine the result of evaluating:

(snowflake-2 100 4 (lambda (level) (if (odd? level) + -)))

What to turn in: For problem 3, please submit the snowflake-2 and side-2.

Problem 4: Calculating the length of the snowflake figure

Principle: Functional programming vs. side effects.

Write two new procedures side-length and snowflake-length,that take the same type of arguments as the original procedures. However, instead of drawing anything, snowflake-length should return the total length of the figure that snowflake draws (i.e., the total distance moved by the pen), given the same arguments.

The overall structure of the two new procedures should be the same as the original, but each should return the length of the part of the figure that would have been drawn. It should be possible to do this with a fairly minimal change to the original.

What to turn in: For problem 4, please submit a listing of these procedures side-length and snowflake-length and [optically] a printout of the output generated by the following code (add it as a comment):

(snowflake-length 100 4)

Note you get an exact result, you could also get a floating point number by evaluating:

(snowflake-length 100.0 4)

Perfect Snowflake Contest (Optional)

Hopefully, you generated some interesting snowflakes in the course of this assignment. If you wish, you can select your best designs and enter them in the CS212 Perfect Snowflake Contest. Submit the code which generates your snowflake and a printout of the result -- the code should be part of the file that you will send, but the printout should be given in the section on Monday evening (2/8) or the lecture on Tuesday morning (2/9). To be fair, please do not turn in more than two pictures. Designs will be judged by the CS212 staff. The winner will receive a prize.