Parsing is something we do constantly. In fact, you are doing it right now as you read this sentence. Parsing is the process of converting a stream of input into a structured representation. The input stream may consists of words, characters, or even bits. The output of the process is a tree.
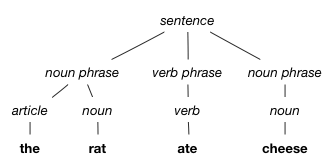
Our brains are remarkably good at parsing. When we hear a sentence like “The rat ate cheese,” our brains build a parse tree similar to the following diagram:

Notice that the leaves of the tree, in left-to-right order, spell out the sentence, but there are also some other nodes higher up in the tree describing the function of each words and of subsequences of words.
Your brain can handle much more complex sentences, though it does have its limits. On the other hand, when you read a supposed sentence like “rat cheese the ate the,” you instantly recognize this as not being a sentence at all, because it has no parse tree. This sequence of words is, in fact, a syntax error.
Parsing is performed by computers as well. Your Java programs are parsed by the Java compiler. Even more mundane devices such as calculators use parsing to interpret mathematical expressions.
For programming languages, legal syntax is defined by a grammar, which specifies which input sequences have a parse tree. While the situation in real human languages is more complex, for programming languages, legal syntax is defined using a context-free grammar. The modifier context-free means that the legal syntax for a subtree of the parse tree (say, the possible subtrees of a “noun phrase” node, above) depends only on the node at the root of the subtree and not on the rest of the tree.
The grammar is defined in terms of terminal symbols (also
called tokens) and nonterminal symbols. The terminal symbols
can appear as part of the input (e.g., “rat”) and appear in the parse
tree only at its leaves. The nonterminal symbols (e.g., “noun phrase”)
appear at all other nodes in the tree.
There is usually a low-level preprocessing step called tokenization
that reads a stream of raw input symbols and organizes them into a sequence of tokens
to be presented to the parser. For example, when parsing the arithmetic expression
(42 + foo) * 2112, a tokenizer might break the input up into a
sequence of tokens (, 42, +, foo, ), *, and 2112.
A context-free grammar is defined by a set of productions that define how a single nonterminal can be expanded out into a longer series of symbols. A given nonterminal can have multiple different productions specifying alternative ways to expand it. For example, we can write a pseudo-English grammar corresponding to the parse tree above:
sentence → noun-phrase verb-phrase noun-phrase sentence → noun-phrase verb-phrase noun-phrase → noun noun-phrase → article noun noun → adjective noun article → the | a | an adjective → young | old | red | ... noun → cat | dog | rat | cheese | ... verb → eats | barks | ...
As an abbreviation, when a single nonterminal has multiple productions, we write them all together on the right side separated by a vertical bar.
One of the nonterminals in a context-free grammar is designated as the start symbol; it is the root of every possible parse tree. The leaves of the parse tree are terminals, and every other node is a nonterminal whose children correspond to one of the productions in the grammar.
The language of a grammar is the set of strings of terminal symbols that can be produced by constructing a parse tree with that grammar: the possible strings that can be derived from the start symbol. The job of a parser is to figure out whether an input string is part of the language of the grammar and to construct a parse tree if so.
The language of a grammar can be infinite in size if the grammar is recursive. For example, the productions noun-phrase → article noun and noun → adjective noun allow us to derive the following noun phrases: “the dog”, “the old dog”, “the old old dog”, “the old old old dog”, and so on ad infinitum.
With some grammars, it is possible for a string to have more than one parse tree. Such a grammar is said to be ambiguous.
An example of an ambiguous grammar is the following grammar for arithmetic expressions:
E → n | E + E | E × E | ( E )
The symbols n, +, ×, (, and ) are all terminals and the only nonterminal is the start symbol E. The symbols n stands for all possible numeric literals.
With this grammar, a string like “2 + 3 × 5” has two possible parse trees, as shown:

Two parse trees for “2+3×5”
Only one of these parse trees corresponds to our usual understanding of the meaning of the expression as arithmetic, namely the one on the left. Usually, we want the grammars we write to be unambiguous so that we obtain a unique parse tree corresponding to the meaning of the expression. Unfortunately, there is no algorithm that can determine in general whether a given grammar is ambiguous (the problem is said to be undecidable). However, in practice it is possible to design grammars in such a way that ambiguity is avoided.
The problem with the parse tree on the right is that it violates our expectations about precedence. By convention, multiplicative operations have higher precedence than additive operations, but the parse tree on the right violates this custom, because the addition is performed first.
To remove the ambiguity and obtain the expected precedence, the grammar can be rewritten to use more nonterminals. We add more nonterminals to prevent a “+” production from appearing directly under a “×” production. Here T represents an operand in an additive expression and F represents an operand in a multiplicative expression. The productions in this grammar prevent a T from appearing under an F in the parse tree unless shielded by parentheses:
E → E + T | T T → T × F | F F → n | ( E )
This grammar has exactly the same language as the above grammar but is unambiguous. For example, the example string parses uniquely as follows:

THe idea of recursive-descent parsing, also known as top-down parsing, is to parse input while exploring the corresponding parse tree recursively, starting from the top.
Let's build a parser using the following methods.
For simplicity, we will assume that the input arrives
as tokens of type String. We assume
there is a special token EOF at the end of the stream.
/** Returns the next token in the input stream. */ String peek(); /** Consumes the next token from the input stream and returns it. */ String consume();
Using these two methods, we can build two more methods that will be especially useful for parsing:
/** Returns whether the next token is {@code s}. */
boolean peek(String s) {
return peek().equals(s);
}
/** Consume the next token if it is {@code s}.
* Throw {@code SyntaxError} otherwise.
*/
void consume(String s) throws SyntaxError {
if (peek(s)) { consume(); }
else throw new SyntaxError();
}
The idea of recursive-descent parsing is that we implement a separate method for each nonterminal. The content of each method corresponds exactly to the productions for that nonterminal. The key is that it must be possible to predict from the tokens seen on the input stream which production is being used. Recursive-descent parsing is therefore also known as predictive parsing.
The grammar above ensures that the operators + and × are left-associative (operations of equal precedence are performed left-to-right). For the purpose of the exposition, let us temporarily change the grammar to make them right-associative:
E → T + E | T T → F × T | F F → n | ( E )
We will show later how left-associativity can be regained.
The method to parse a string generated by the nonterminal E first recursively parses a string generated by T (because both productions for E start with T), then peeks ahead at the next token to see if it is a +. This determines whether the input contains a string generated by T + E or just T, thereby determining which production to apply next.
// E → T + E | T
void parseE() throws SyntaxError {
parseT();
if (peek("+")) {
consume();
parseE();
}
}
Similarly, the method parseT looks for “×” to decide which
production to use:
// T → F × T | F
void parseT() throws SyntaxError {
parseF();
if (peek("×")) {
consume();
parseT();
}
}
And parseF() can decide using the first symbol it sees,
assuming we have an appropriate method isNumber():
// F → n | ( E )
void parseF() throws SyntaxError {
if (isNumber(peek())) {
consume();
} else {
consume("(");
parseE();
consume(")");
}
}
So far, the parser we have built is only a recognizer that decides
whether the input string is in the language generated by the grammar, i.e. whether
it has a parse tree. It halts normally if so and throws a SyntaxError if not.
It doesn't actually build the parse tree or evaluate the expression.
However, with a few minor modifications, we can easily convert it
into an evaluator that evaluates the expression.
The result type of all the methods becomes int.
int parseE() throws SyntaxError {
int v = parseT();
if (peek("+")) {
consume();
v = v + parseE();
}
return v;
}
int parseT() throws SyntaxError {
int v = parseF();
if (peek("×")) {
consume();
v = v * parseT();
}
return v;
}
int parseF() throws SyntaxError {
if (isNumber(peek())) {
return Integer.parseInt(consume());
} else {
consume("(");
int ret = parseE();
consume(")");
return ret;
}
}
Now we can parse the previous example input and get a result of 17.
The output of a parser is usually an abstract syntax tree (AST), which differs from a parse tree in that it contains no noninformative terminal symbols. For example, if we parse the input 2+(3×5), we expect to get a tree like the following,

Abstract syntax tree
Note that the parentheses are no longer there! Parentheses are only needed in the input string to disambiguate parsing. Once the expression is parsed, they are no longer needed, because the tree structure determines the evaluation order. In fact, the expressions 2+(3×5) and 2+3×5 should produce exactly the same AST. Note also that the tree does not need to keep track of nonterminals like T and F.
The abstract syntax tree is implemented as a data structure. However, unlike the tree structures we have seen up until this point, the nodes are of different types.
class Expr {}
enum BinaryOp { PLUS, TIMES }
class Binary extends Expr {
BinaryOp operator;
Expr left, right;
Binary(BinaryOp op, Expr l, Expr r) {
operator = op;
left = l;
right = r;
}
}
class Number extends Expr {
int value;
Number(int v) { value = v; }
}
Using these classes, we can build the AST shown in the previous figure:
Expr e = new Binary(BinaryOp.PLUS,
new Number(2),
new Binary(BinaryOp.TIMES, new Number(3), new Number(5)));
A parser that constructs an AST can now be written by changing our recognizer once more, this
time to return an Expr. Instead of computing integers, as in the evaluator, we just
construct the corresponding AST nodes:
Expr parseE() throws SyntaxError {
Expr e = parseT();
if (peek("+")) {
consume();
e = new Binary(BinaryOp.PLUS, e, parseE());
}
return e;
}
Expr parseT() throws SyntaxError {
Expr e = parseF();
if (peek("×")) {
consume();
e = new Binary(BinaryOp.TIMES, e, parseT());
}
return e;
}
Expr parseF() throws SyntaxError {
if (isNumber(peek())) {
return new Number(Integer.parseInt(consume()));
} else {
consume("("); // parentheses discarded here!
Expr e = parseE();
consume(")");
return e;
}
}
Some grammars cannot be parsed top-down. Unfortunately, they include grammars that we might naturally want to write. Particularly problematic are grammars that contain left-recursive productions, where the nonterminal being expanded appears on the left-hand side of its own production. We saw these in the original grammar specifying the left-associative operators + and ×. The production E → E + T is left-recursive, whereas the production used above, E → T + E, is right-recursive. A left-recursive production doesn't lend itself to predictive parsing, because top-down construction of the AST means the parser needs to be able to choose which production to use based on the first symbol seen.
Grammars with left-recursive productions are very useful, because they create parse trees that describe left-associative (left-to-right) computation. With the right-recursive production used above, the string “1 + 2 + 3” creates an AST in which evaluation proceeds right-to-left. Programmers normally expect left-to-right evaluation, and this is even more of a problem if the operator in question is not associative (for example, subtraction).
To fix this, we can reassociate after parsing. To see how this works, note that the two productions E → T + E | T can be viewed as shorthand for an infinite list of productions:
E → T
E → T + T
E → T + T + T
E → T + T + T + T
...
Another way to express all these productions is to adapt the Kleene star notation used in regular expressions: the expression A* means 0 or more concatenated strings, each chosen from the language of A. For example, if the language of A is {"a", "bb"}, then the language of A* has an infinite number of elements, including "a", "aa", "aaa", "bb", "bbbb", "abba", "bbabbbb", and many more.
Using the Kleene star notation, we can rewrite the infinite list of productions:
E → T ( + T )*
where the parentheses are being used as a grouping construct (they are metasyntax rather than syntax).
The point of rewriting the productions in this way is that parsing a use of Kleene star naturally lends itself to an implementation as a loop. Within that loop, the AST can be built bottom-up, so that the operator associates to the left:
void parseE() throws SyntaxError {
Expr e = parseT();
while (peek("+")) {
consume();
e = new Binary(BinaryOp.PLUS, e, parseT());
}
}
Given input “t0 + t1 + t2 + t3 + ...”, the corresponding abstract syntax tree built by this code looks as follows:

Because it allows parsing of left-associative operators, reassociation via bottom-up tree construction is an important technique for top-down parsing.