Assignment 6: Interactive image selection, part II
In Assignment 5 you developed a graphical application to extract subjects from images by drawing a polygon around them one edge at a time. But that approach is tedious and imprecise for subjects with curved edges. It would be convenient if the program could automatically trace such edges.
Fortunately, there is an algorithm named “intelligent scissors” to do just that, and it is based on finding shortest paths in graphs (which we’ve just covered in lecture). Your task on this assignment is to implement the data structures and algorithms required by “intelligent scissors” and to tune the way it weights edges in its graph so that it works robustly on as many subjects as possible.
Learning Objectives
- Implement a Priority Queue using a heap and pair it with a Dictionary to support efficient priority changes.
- Implement Dijkstra’s algorithm to find shortest paths in a weighted graph.
- Provide polymorphic behavior by implementing multiple subclasses of a parent type and overriding the parent’s behavior.
- Extend
SwingWorkerin order to perform an expensive computation concurrently with an interactive GUI. - Perform calculations on neighborhoods of pixels in a color image.
- Experiment with custom weights in the “intelligent scissors” algorithm to more accurately follow edges in images.
Collaboration Policy
On this assignment you may work together with one partner. Having a partner is not needed to complete the assignment: it is definitely do-able by one person. Nonetheless, working with another person is useful because it gives you a chance to bounce ideas off each other and to get their help with fixing faults in your shared code. If you do intend to work with a partner, you must review the syllabus policies pertaining to partners under “programming assignments” and “academic integrity.”
Partnerships must be declared by forming a group on CMSX before starting work. The deadline to form a CMS partnership is Friday, Dec 6, at 11:59 PM. This is to make sure you are working with your partner on the entire assignment, as required by the syllabus, rather than joining forces part way through.
As before, you may talk with others besides your partner to discuss general course concepts, but you must never show your code to another student who is not your partner. Consulting hours are the best way to get individualized assistance at the source code level if you get stuck diagnosing an issue.
Since A6 is a continuation of A5, we should clarify how the Academic Integrity policy applies to your base code. You are not required to work with same partner on A6 as you did on A5. If you do work with a partner on A6, you may use either of your A5 submissions as a starting point. However, you may not use any other student’s code—at least one partner must be able to assert original authorship of the base code. As usual, both partners must claim joint authorship of all new A6 code and are responsible for understanding and attesting the origin of all code they submit.
Frequently asked questions
If needed, there will be a pinned post on Ed where we will collect any clarifications for this assignment. Please review it before asking a new question in case your concern has already been addressed. You should also review the FAQ before submitting to see whether there are any new ideas that might help you improve your solution.
Assignment overview
The end goal (“functional requirements”)
You will extend the Selector application from A5 so that users can choose from among several alternative selection tools. One is the “point-to-point” model from before that connects control points with straight lines, but another will use the “intelligent scissors” algorithm to connect control points with a path that tries to follow “edges” in the image. Users can switch between models while building up a selection, allowing them to quickly use straight lines for some segments and to use edge-following paths for others.
Because the “intelligent scissors” algorithm is expensive, a progress bar will let the user know how long they have to wait before adding their next point.
The GUI will remain responsive during this time, and the user will have the option to cancel the operation if it is taking too long.
All of the features of the original Selector application should continue to work without modification, since they only depend on the SelectionModel supertype.
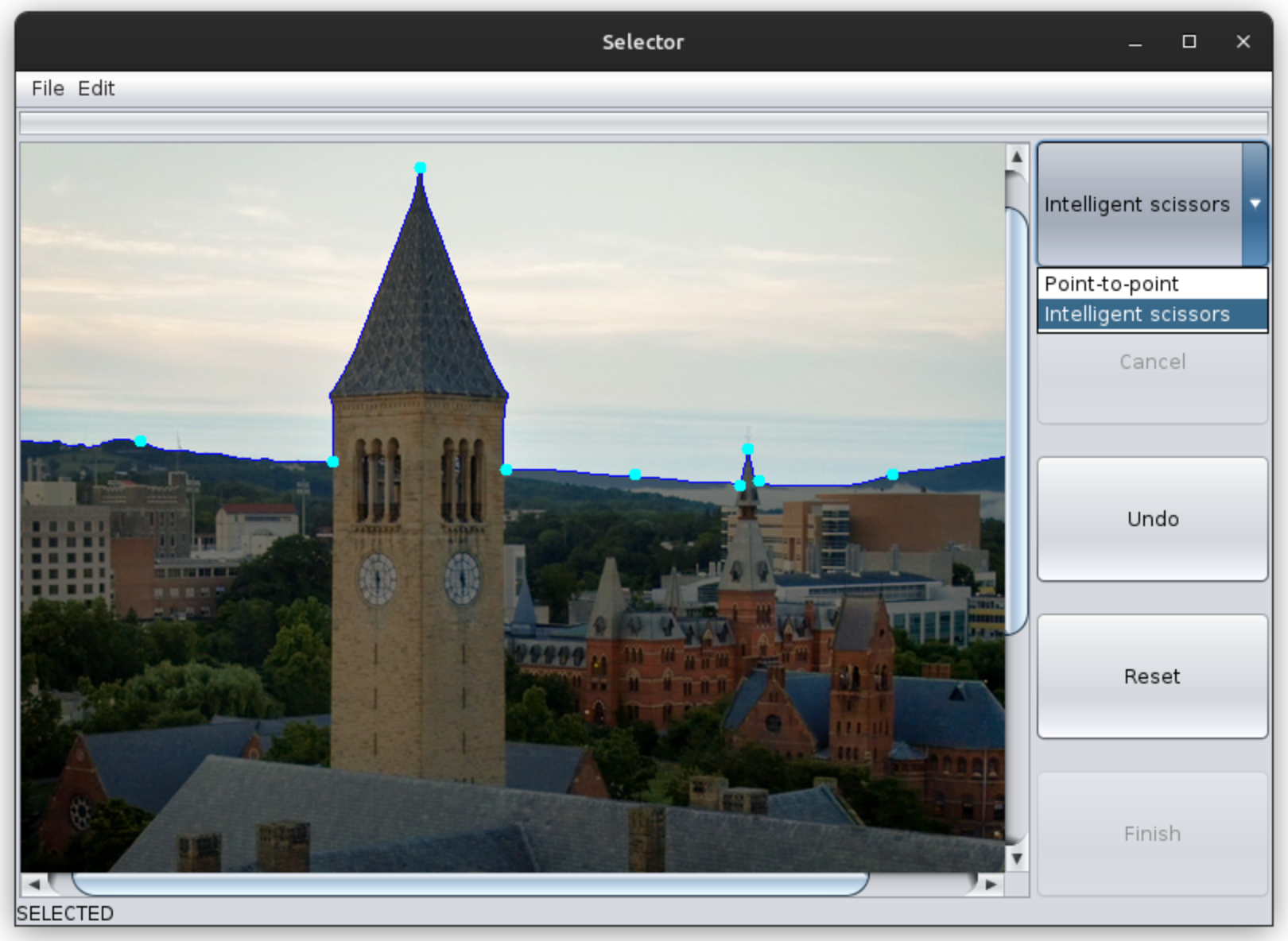
There is no unique “best way” for the intelligent scissors algorithm to identify “edges” in an image, and what works well for some images may not work as well for others. You will be provided with a basic “weight function” that works well on black-and-white images, but you should experiment with different functions that might perform better. Users will be able to select among all available weight functions when choosing their selection tool.
Intermediate objectives
The “intelligent scissors” algorithm requires data structures and algorithms related to Graphs, which you will be responsible for implementing:
- You will need to implement Dijkstra’s shortest paths algorithm for a generic Graph. To support the progress bar, you must be able to advance the algorithm incrementally, giving clients a chance to do other work before all vertices have been settled. Clients should be able to use these intermediate results to see which vertices have been discovered and settled and to find paths to any discovered vertices.
- You will need to implement a Min Priority Queue using a heap. The queue must support efficiently changing an element’s priority, which will accelerate your shortest paths algorithm.
With these in hand, you will implement a new subclass of SelectionModel: ScissorsSelectionModel.
Since finding shortest paths in images can be slow, this model will take advantage of “processing” states (e.g., ADDING, MOVING) and will use a SwingWorker (that you will implement) to do the work on a background thread.
The weights of the graph edges considered by Dijkstra’s algorithm should depend on the brightness and color of nearby pixels in the image, but there are multiple ways this could be done.
The notion of edge weights has been moved to a separate Weigher type, rather than being part of the Graph interface, and you will try out different ways to define edge weights by implementing your own Weigher classes.
Recommended timeline
- Day 1: Read the “Assignment overview” and “Preliminaries” sections of this handout. Per these instructions, extract the release code, copy your A5 files on top of it, and make the required changes to this base code. Then complete the tasks in “step 0” to enhance the GUI.
If your merged project does not run, seek help from office or consulting hours immediately. And if your A5 submission had bugs, you’ll want to get those fixed. - Day 2: Read the handout section on the Intelligent Scissors algorithm. Complete the tasks in “step 1” (implementing
ShortestPaths). - Day 3: Read the handout section on
SwingWorker. Complete the tasks in “step 2” (implementingScissorsSelectionModel, including its innerSwingWorkersubclass, and updatingSelectorApp). - Day 4: Complete the tasks in “step 3” (implementing
MinQueue). - Day 5: Read the handout section on edge weights. Complete the tasks in “step 4” (defining an improved weighting function). Note that this step will be worth the fewest points, so focus on getting the preceding ones working before attempting this.
Finally, respond to the questions in the reflection document. Have fun using the program to cut out more detailed stickers!
Preliminaries: Updating A5 code
Your A5 submission will serve as the starting point for A6.
(If you were not able to produce a submission for A5, reach out to the instructor ASAP.)
Most of your work for A6 will be in the new graph and scissors packages, but you will also need to make a few changes to familiar code in the selector package.
We recommend the following procedure:
- Download the A6 release code and open it as a new project in IntelliJ.
- Copy the files you submitted for A5 (SelectorApp.java, SelectionModel.java, PointToPointSelectionModel.java, and SelectionComponent.java) into the “src/selector” folder of your new A6 project. Check that your app still runs.
- Make the changes described below (note: these changes are all marked with a “New in A6” or “TODO A6” comment in the A6 release code, which you can reference if there’s any ambiguity).
Changes in selector package
1. Add progress bar to SelectorApp
Add the following field to SelectorApp:
// New in A6
/**
* Progress bar to indicate the progress of a model that needs to do long calculations in a
* "processing" state.
*/
private JProgressBar processingProgress;
Then, in SelectorApp’s constructor, initialize this field and add it to your frame above the image.
For example:
// New in A6: Add progress bar
processingProgress = new JProgressBar();
frame.add(processingProgress, BorderLayout.PAGE_START);
Finally, in setSelectionModel(), listen for “progress” events from the model in addition to “state” events:
// New in A6: Listen for "progress" events
model.addPropertyChangeListener("progress", this);
You will respond to these new events in TODO A6.0B.
2. Add new painting routines to SelectionComponent
In SelectionComponent.paintComponent(), add the following code at the end of the method.
This will let you visualize the processing being performed by fancier selection models.
In particular, for “intelligent scissors”, it will highlight which pixels are settled, in the frontier set, or undiscovered as Dijkstra’s algorithm proceeds in real time.
// New in A6: Paint processing progress (if we recognize its type)
if (model.state().isProcessing()) {
Object progress = model.getProcessingProgress();
if (progress instanceof ImagePathsSnapshot) {
paintPathfindingProgress(g, (ImagePathsSnapshot) progress);
}
}
Then define the following new method to actually perform the highlighting (don’t worry if you don’t understand some of the details here, like “clip bounds” and “ARGB”; you can look them up if you like, but they’re not part of this assignment’s learning goals):
// New in A6
/**
* Shade image pixels according to their current path search status (settled, frontier, or
* undiscovered). Do nothing if there is no pending path solution.
*/
private void paintPathfindingProgress(Graphics g, ImagePathsSnapshot pendingPaths) {
int settledColor = new Color(192, 192, 96, 128).getRGB();
int frontierColor = new Color(96, 96, 192, 128).getRGB();
Rectangle bounds = g.getClipBounds();
int width = Math.min(bounds.width, model.image().getWidth() - bounds.x);
int height = Math.min(bounds.height, model.image().getHeight() - bounds.y);
BufferedImage img = new BufferedImage(width, height, BufferedImage.TYPE_INT_ARGB);
for (int x = bounds.x; x < bounds.x + width; ++x) {
for (int y = bounds.y; y < bounds.y + height; ++y) {
Point p = new Point(x, y);
if (pendingPaths.settled(p)) {
img.setRGB(x - bounds.x, y - bounds.y, settledColor);
} else if (pendingPaths.discovered(p)) {
img.setRGB(x - bounds.x, y - bounds.y, frontierColor);
}
}
}
g.drawImage(img, bounds.x, bounds.y, null);
}
For these to compile, you will need the following additional import statements at the top of the file (accepting IntelliJ’s suggestions will probably do the trick):
import java.awt.Rectangle;
import scissors.ImagePathsSnapshot;
Step 0: GUI additions
A6 includes a new implementation of the SelectionModel interface—scissors.ScissorsSelectionModel—and instances are configured with the name of a Weigher algorithm, of which there may be several.
Users should be able to choose which model & weight to use when drawing their selection.
Note that the models are designed to initialize their state from an existing model when possible (by passing it as a constructor argument), so users can mix-and-match some selection tools while tracing a single subject in their image.
Back in A5, you added a “combo box” for selecting between the “point-to-point” and “spline” selection models.
Modify your SelectorApp.makeControlPanel() to add an option for “Intelligent scissors: gray”, per the following TODO:
// TODO A6.0a: Add the following option to your control panel's model selector:
// * Intelligent scissors: gray (`ScissorsSelectionModel` with a "CrossGradMono" weight
// name). You will need to `import scissors.ScissorsSelectionModel` to use this class.
Next, turn your attention to your new progress bar.
Now that the app is listening for “progress” events, we should respond to those events by making the progress bar move.
Additionally, progress bars often have an “indeterminate” mode that shows an animation indicating that work is being done, even though a progress percentage isn’t known.
Your app should put the progress bar into “indeterminate” mode whenever its selection model enters any state state that is “processing” and leave that mode as soon as it gets a progress update (or leaves a “processing” state).
Complete the following TODO in propertyChange() (while retaining the existing call to reflectSelectionState()):
// TODO A6.0b: Update the progress bar [1] as follows:
// * When the model transitions into a state that is "processing", set the progress bar to
// "indeterminate" mode. That way, the user sees that something is happening even before
// the model has an estimate of its progress.
// * When the model transitions to any other state, ensure that the progress bar's value is
// 0 and that it is not in "indeterminate" mode. The progress bar should look inert if
// the model isn't currently processing.
// * Upon receiving a "progress" property change, set the progress bar's value to the new
// progress value (which will be an integer in [0..100]) and ensure it is not in
// "indeterminate" mode. You need to use the event object to get the new value.
// [1] https://docs.oracle.com/javase/tutorial/uiswing/components/progress.html
Unfortunately, you won’t be able to appreciate these efforts until you’ve completed ScissorsSelectionModel below, but this gets all of the GUI work out of the way.
Now on to graphs!
Step 1: Shortest paths
Intelligent Scissors and Graphs
Images are normally considered as matrices (2D arrays) of pixels.
We can treat an image as a Graph by considering each of its pixels to be a vertex, connected to each of their 8 neighbors (including diagonals) with an edge (visualized as connecting the pixels’ centers).
Each segment of a selection in an image can therefore be interpreted as a sequence of these edges (i.e., a path in the graph) connecting the pixels on the boundary of the selection.
The “intelligent scissors” algorithm simply creates these segments by finding the shortest path in the graph between two user-defined “control point” pixels.
And since Dijkstra’s algorithm finds the shortest paths from a starting point to all of the other pixels in the image, once it has been run, it can quickly provide these paths to whatever location the mouse pointer is hovering over, providing the “live wire” feature of our Selector application.
The “intelligence” in the algorithm is all about defining the weight of each edge, which will be discussed later.
To allow you to experiment with different weight formulas, weights are computed by a separate Weigher object.
We will use a very general Graph interface that provides just enough functionality for running Dijkstra’s algorithm when paired with a compatible Weigher object.
The interface has a VertexType type parameter for specifying the type of its vertices, which must be a subclass of Vertex; Vertex in turn has an EdgeType parameter specifying the type of its edges.
Vertices are labeled with an integer ID, which can be more efficient to use than a Vertex object in some situations (and image graphs have a lot of vertices, so efficiency matters).
The file “ImageGraph.java” implements the Graph, Vertex, and Edge interfaces for images, providing convenient methods to get a vertex from its pixel location (x and y coordinates).
However, your implementation of Dijkstra’s algorithm should work with any implementation of these interfaces (the provided test suite defines a simple alternative implementation named SimpleGraph).
Implementing Dijkstra’s algorithm
Study the provided source code in the graph package, especially ShortestPaths and PathfindingSnapshot.
Keep in mind that their code in this package should only depend on the Graph, Vertex, and Edge interfaces, not on any of the specifics for image graphs.
Pay attention to the fields in ShortestPaths, noting that distances and predecessors are stored in arrays indexed by vertex IDs, rather than in a Map.
This is an optimization, as int arrays require less space than collections of objects, and those savings add up when dealing with millions of pixels.
Read the MinQueue interface to learn how to interact with the frontier set.
Complete TODO A6.1a by implementing Dijkstra’s algorithm.
Note that extendSearch() does not necessarily find all shortest paths in a single invocation; repeated calls may be necessary.
This allows clients to pause the search periodically in order to do things like update a progress bar (which you will take advantage of in the next part).
Once you have implemented the algorithm, you can start to check your work with the test cases in TestShortestPaths (the distance checks should pass, but the path checks require the next task).
extendSearch() (as well as the findAllPaths() convenience method) returns a PathfindingSnapshot, which can be used to find paths from its starting node to any “discovered” destination node (and if the destination node is “settled”, then the returned path will be the shortest path).
Complete TODO A6.1b to compute these paths from the saved data.
Check your work by running the full test suite.
Step 2: Intelligent Scissors selection model
Now that you can find shortest paths in graphs, it’s time to turn your attention to images in particular.
ScissorsSelectionModel is a subclass of SelectionModel, meaning that it can substitute for PointToPointSelectionModel in your Selector app.
Unlike with point-to-point selections, its PolyLine segments will contain many points (so hopefully you didn’t assume straight-line segments in your A5 solution—remember to only assume things guaranteed by the SelectionModel interface).
Read the class invariants for ScissorsSelectionModel; note in particular that its paths field stores the (final) results from the shortest-paths search starting at the most recently added control point.
Based on this, complete TODOs A6.2A and A6.2B (you will find the ImageGraph pathToPolyLine() method helpful) to create selection segments from the last control point to the provided location.
Note that you are using the results of shortest paths that have already been solved; there is no need to solve for new paths until the end of appendToSelection(), where you call findPaths() with the new endpoint to do so.
Note that whenever a new point is added to the selection, shortest paths must be found again using it as the starting point; once they are found, the “live wire” will work as expected.
Since finding paths can be slow, we must not perform that work on the EDT.
This findPaths() method uses a SwingWorker to do that work on a background thread.
ShortestPathsWorker
The ShortestPathsWorker class will test your understanding of inheritance, scope, and threads, so take some time to study its design.
First, it is a subclass of SwingWorker<FinalReturnType, IntermediateResultType>, meaning it can use all of the methods inherited from its superclass and can override some to specialize their behavior.
The type parameters indicate the types of the final and intermediate results produced by the worker; in this case, they are both PathfindingSnapshot (which can represent either intermediate or final shortest paths).
The methods we will override are doInBackground() (which actually performs the expensive task), process() (which responds to intermediate results) and done() (which handles the final result).
ShortestPathsWorker is also an inner class of ScissorsSelectionModel, which means that it has an implicit reference to the model object that created it and can access all of that model’s fields (even private ones) without qualification, as they are in scope.
This makes it convenient for the worker to manipulate its outer object’s state, such as by reassigning the paths field or firing property change events.
But we need to be careful to only do this from Swing’s Event Dispatch Thread, and we need to be careful to avoid having two workers active at the same time.
Finally, ShortestPathsWorker is designed to be a “bridge” that helps two threads communicate, which means you need to pay careful attention to which methods run on which threads, especially since you won’t actually call your overridden methods yourself (remember inversion of control).
The process() and done() methods are guaranteed to be called (by Swing) on the EDT, so it is safe for them to access the fields of the outer model object.
In contrast, the doInBackground() thread will be called on a separate worker thread, so it must not access its outer model object.
It may access the pathfinder field, and it may call inherited methods like setProgress(), publish(), and isCancelled().
We’d like to avoid having two workers running simultaneously, since we wouldn’t know which one would finish first.
This is why the “Finish” button and SelectionComponent mouse listeners are disabled in any state that is processing.
So long as the worker itself is the only code that will ever transition out of a processing state, we prevent other workers from being started before the current one has finished.
Unfortunately, there’s a subtle hole in this solution: if the model is reset, it will transition back to NO_SELECTION immediately.
This might be desirable in case your worker encounters an infinite loop, but it requires additional care.
This is reflected in the class invariant for the worker field, which must be set to null whenever the model leaves a processing state.
Using this convention, if a worker ever sees that it’s outer model’s worker field doesn’t point to itself, its can return immediately without making any changes to the model.
Implement TODOs A6.2C & A6.2D, following the procedures outlined in the release code.
Thanks to your GUI preparations above, you should be able to test this in your app as soon as you finish implementing your worker! Just choose “intelligent scissors: gray” from your combo box. This gives you a way to visualize the progress of Dijkstra’s algorithm, highlighting the frontier between “settled” and “undiscovered” pixels. Visualizing algorithms can be a great way to improve your understanding of them, and it can also help you spot bugs that aren’t caught by unit tests.
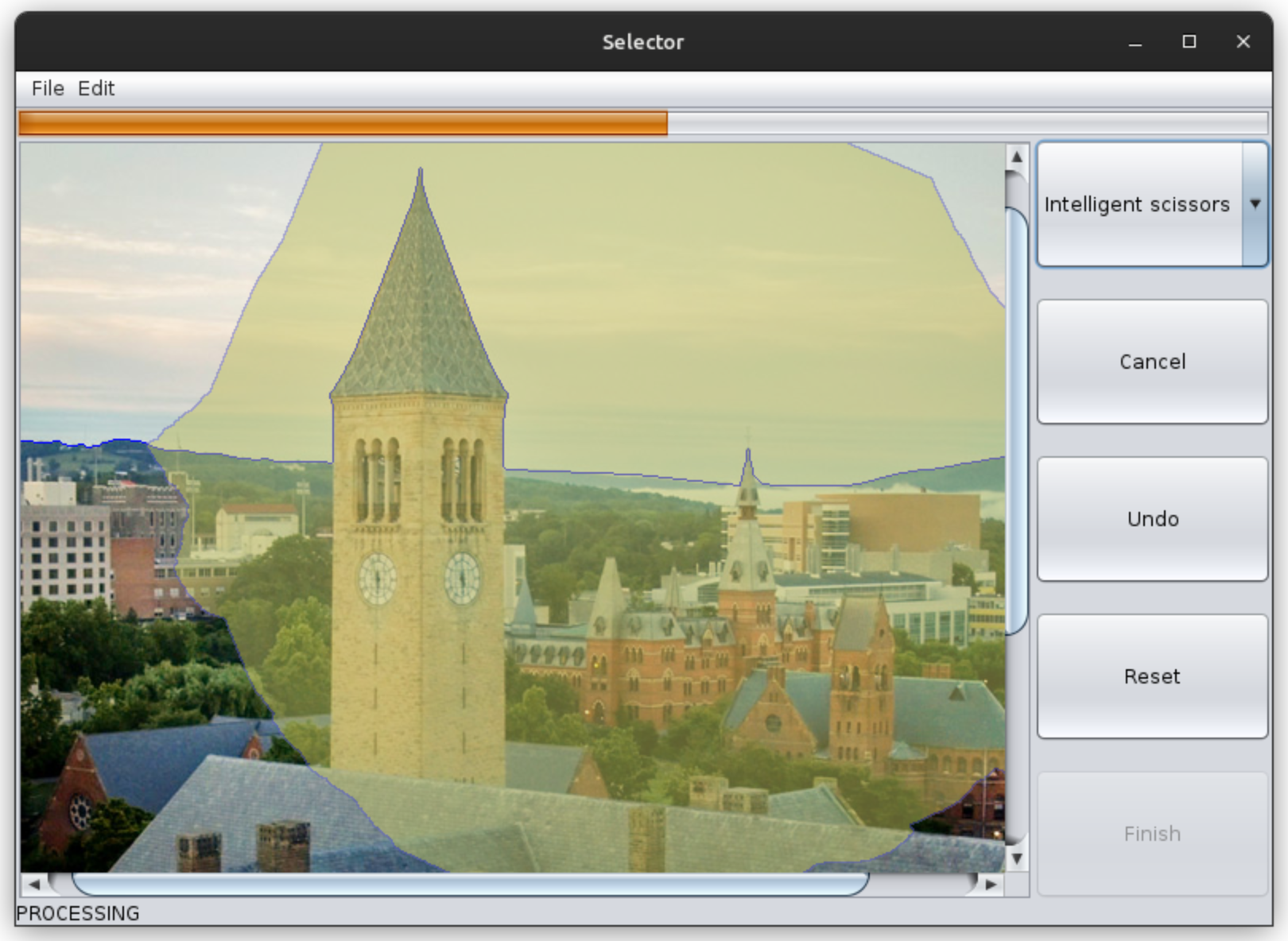
Be sure to test all the features of your app: adding points, finishing selections, moving points, cancelling solves, and resetting. It should feel like a robust and responsive application: no error messages, no stalling while browsing menus or resizing the window, and no inconsistent views or behavior. Feel free to use a smaller image for testing in order to speed things up, as the “reference” priority queue implementation you are currently using is quite slow. In fact, that’s what you’ll work on improving next.
It would be great to have a unit test suite for ScissorsSelectionModel, and you are welcome to create your own, using what you’ve learned about wait() and notifyAll() to wait for processing to finish before checking postconditions.
But no such suite exists in the release code at this time.
Step 3: Priority queue
This step requires concepts from Lecture 27 (heaps). Feel free to move on to Step 4 and return to this later if that lecture has not yet taken place.
The release code for ShortestPaths used a simple class named RefMinQueue to represent the frontier set.
But it has a very inefficient addOrUpdate() method that slows down the “intelligent scissors” algorithm considerably.
Your next task is to implement HeapMinQueue as a replacement, using a hash table “index” to speed up updates.
Study the provided source code for graph.HeapMinQueue, paying careful attention to its invariants.
You will need to implement its methods for adding, removing, and updating elements.
We recommend doing so in this order:
- TODO A6.3A: Implement
swap(), which will be useful in future methods and will give you practice maintaining the class invariant (sinceheapandindexneed to stay in-sync). - TODO A6.3B: Define “bubble up” and “bubble down” helper methods for the binary heap data structure, using
swap()to help you maintain the class invariant. Don’t forget to write clear specifications! - TODO A6.3C: Implement
remove(), with the help of yourswap()and “bubble down” methods. - TODO A6.3D: Implement
add()with the help of your “bubble up” method. You can now run the provided test cases that don’t involve updates. - TODO A6.3E: Implement
update()and test your work with the provided test cases.
The provided test suite is reasonably thorough, especially when combined with the class’s thorough invariant checks, so you can have high confidence in your implementation when the tests all pass.
Once your priority queue passes the test cases, replace the RefMinQueue with a HeapMinQueue in ShortestPaths and try running your application again.
With assertions disabled, it should be much quicker than before!
Asserts and performance
As usual, we recommend running your program with assertions enabled at first, using the -ea VM flag.
Remember that IntelliJ enables them by default when running unit tests, but you need to add this flag yourself when running the Selector application.
However, the checkInvariant() method of our HeapMinQueue, while very good at catching bugs, is very expensive, which will slow your program to a crawl when working with large images.
While this is convenient for checking that your progress bar works, you will probably want to disable assertions for SelectorApp (by removing the -ea VM flag) after a few tests so you can appreciate the speedup provided by your efforts.
Step 4: Edge weights and digital images
Looking back at step 0, what was that “CrossGradMono” you passed to ScissorsSelectionModel?
And how does the model’s pathfinding manage to avoid taking “shortcuts” that cut across your subject most of the time?
The answer can be found in the ScissorsWeights class, which houses the different Weigher implementations users should be able to pick from.
This class also acts as a factory for Weighers, allowing them to be created from a string like “CrossGradMono”.
Intuitively, we want edges to have a small weight if they run parallel to a subject boundary and a big weight if they cross a subject boundary. But your weight function doesn’t know what a “subject” is; it is limited to doing math on pixel brightness values. Finding a weight function that is effective for many different kinds of subjects in different kinds of images (think cartoon vs. photograph) is therefore as much a creative endeavour as a technical one.
We provide a sample weight function in the class CrossGradMonoWeight that works reasonably well.
To see how it’s motivated, consider a grayscale image, and then imagine that each pixel is a tower rising out of the image whose height is proportional to its brightness.
The image now looks like a hilly landscape with mountains in the bright portions, valleys where it’s dim, and plains where it’s mid-grey.
We would like our selection to follow “ridgelines” in this landscape—that is, we want the slope of the terrain to be gentile in the direction our path is traveling, but steep perpendicular to it.
In the language of vector calculus, we want the cross product between our edge direction and the image’s gradient to be high.
Unfortunately, this gives us a quantity that’s a bit backwards—it’s a reward function rather than a cost function in that big numbers are good. But since we’re finding minimum-weight paths, we need big numbers to be bad. Yet we also need edge weights to be non-negative. The solution is to subtract our reward from the maximum possible award. So mathematically, if represents the steepest slope in the image, represents the slope of image brightness (in both horizontal and vertical directions), and represents the edge, then our weight function is
(Note that the cost is multiplied by the length of an edge, since diagonal edges are longer than horizontal and vertical ones and should therefore cost more in situations where the perpendicular slope is the same.)
The slope perpendicular to the edge can be approximated by subtracting the brightness of the pixels on either side of the edge, then dividing by how far apart those pixels are, resulting in the math of the crossGrad() function (it only looks ugly because it has to handle 8 different directions; if you draw out a few cases, you’ll see it’s actually pretty simple.)
This formula is a good starting point, but it has some issues. Most notably, it’s “colorblind”—it converts the image to grayscale before applying the above math. If you try your application on the image “challenge_1.png”, you’ll see that it doesn’t follow edges at all—that’s because everything looks like the same shade of gray when the colors are averaged together.
To improve on this, you’ll first need to understand how Java represents color images with its Raster class.
Instead of storing a single brightness value at each pixel location, it stores a separate red brightness, green brightness, and blue brightness.
Java calls these three distinct brightnesses “bands” (another common name for them is “channels”), so a color image typically has 3 bands: one for red, one for green, and one for blue.
The crossGrad() function only considers one band at a time, but you can tell it which band to use (our monochrome weigher only processes band 0, since, in a grayscale image, all of the bands are equal).
Task: An improved Weigher
Your task is to implement an alternative weigher that, at the very least, considers each color band separately so that your app behaves reasonably on the “challenge_1.png” image. Aside from that objective, you can be as creative as you like with this weigher! Think about different ways you could reward edges for following contours in an image, or different ways you could penalize edges that cut across contours. We’ll include a few ideas to consider below.
In order to make use of your new weigher in the app, you’ll need to make changes in a few places. Here’s how we recommend proceeding (TODOs A6.4a–A6.4d):
- Make a copy of
CrossGradMonoWeightwithinScissorsWeightsand give it your own descriptive class name. In its constructor, delete the code that converts the image to grayscale and instead simply initialize the class’s raster with the one from the graph’s image. - Modify
weight()to perform a calculation of your choosing. Be creative! Just be sure to respect these constraints:- Weights must always be non-negative
- You must be able to compute a weight for any edge in the image without throwing an exception (be careful for edges at the image’s boundaries; note how
crossGrad()treats these specially) - Your weigher should improve the selection experience with the challenge image
- Register your weigher with the
ScissorsWeightsfactory so that code can create instances just by knowing its name - Modify your combo box in
SelectorAppto show your new weigher as an option, alongside the old one. Selecting that option should change the model to a new instance ofScissorsSelectionModelconstructed with your new weigher’s name
We look forward to seeing your creativity here! If you’re looking for ideas beyond handling each band separately, here are a few to consider (these all go well beyond the CS 2110 learning objectives—exploring them is just for fun and glory):
- Apply an “edge-detection” filter, such as a Sobel filter, to a copy of the image. Prefer graph edges that move to pixels with high “edginess”. Java’s
ConvolveOpcan help here. - Approximating slopes by subtracting neighboring pixels tends to produce “noisy” results. Consider blurring a copy of the image and computing slopes using the blurred copy. Java’s
ConvolveOpmay again be useful. - The grayscale used by
CrossGradMonoWeightis especially bad because it simply averages all of the bands, yet humans do not see red, green, and blue equally well. Consider making a different grayscale copy of the image that reflects its luminance as perceived by humans (or, for a simpler calculation, its “luma”). Java’sBandCombineOpcan help. - Compute multiple different costs (or use multiple amounts of blur) and add them together to get the benefits of each.
II. Submission
In “reflection.txt”, estimate the amount of time you spent on this assignment, and answer the verification and reflection questions. Then submit the following files:
- SelectorApp.java
- ShortestPaths.java
- PathfindingSnapshot.java
- ScissorsSelectionModel.java
- HeapMinQueue.java
- ScissorsWeights.java
- reflection.txt
Good luck, and have fun!
