Assignment 6: Sewer navigation
Learning Objectives
In this assignment you will gain experience with graph algorithms and concurrency. You will write algorithms to navigate graphs and learn how to test them. You will also practice synchronizing concurrent code. Additionally, you will have the opportunity to optimize your graph searches using various data structures like heaps.
Just as importantly, you will practice working in a large codebase that you did not write yourself. You will need to seek out and read documentation for many classes and methods in order to determine which are relevant to your task, and you will need to juggle your role as “client” vs. “implementer” as you compose new and existing functionality to complete the project.
Introduction
The London Sewer System is well known for its complex web of underground tunnels. In this project you will model and navigate this sewer network, represented as a graph. Our protagonist, McDiver, is tasked with finding a ring with special powers that has been hidden in the sewer. His job is to navigate the maze to find the ring. Fortunately, this does not have to be a completely blind search—McDiver has a detector that can measure the distance to the ring, so he can tell when he is getting closer.
When McDiver finds the ring, it turns out that it is booby-trapped. McDiver is dropped into a lower level of tunnels where there is additional treasure sprinkled all through the maze. Fortunately, McDiver immediately finds the map to this lower level and wants to collect some treasure on the way out. But toxic fumes in the sewer are starting to take a toll. So the goal is to head to the exit in the prescribed number of steps while still picking up as much treasure as possible along the way—quickly enough to avoid falling victim to those noxious fumes!
The student submission that is the most successful at maximizing points will be recognized for excellence by the coveted McDiver Award.
Collaboration Policy
On this assignment you may work together with one partner. Having a partner is not needed to complete the assignment: it is definitely do-able by one person. Nonetheless, working with another person is useful because it gives you a chance to bounce ideas off each other and to get their help with fixing faults in your shared code. If you do intend to work with a partner, you must review the syllabus policies pertaining to partners under “programming assignments” and “academic integrity.”
Partnerships must be declared by forming a group on CMSX before starting work. The deadline to form a CMS partnership is Thursday, November 30. After that, CMSX will not allow you to form new partnerships on your own. You may still email your section TA (CCing your partner) to form a group late, but a 5 point penalty will be applied. This is to make sure you are working with your partner on the entire assignment, as required by the syllabus, rather than joining forces part way through.
As before, you may talk with others besides your partner to discuss Java syntax, debugging tips, or navigating the IntelliJ IDE, but you should refrain from discussing algorithms that might be used to solve the problems, and you must never show your in-progress or completed code to another student who is not your partner. Consulting hours are the best way to get individualized assistance at the source code level.
Frequently asked questions
If needed, there will be a pinned post on Ed where we will collect any clarifications for this assignment. Please review it before asking a new question in case your concern has already been addressed. You should also review the FAQ before submitting to see whether there are any new ideas that might help you improve your solution.
Note that the student handbook has been updated to clarify some of the requirements that apply to all assignments in this course. Please ensure that your submission complies with these to avoid deductions during grading.
Tasks To Complete
The list of concrete tasks you need to complete is given below.
Part 1: Application infrastructure
Task 1: Implement Dijkstra’s algorithm
In this task, you will complete the implementation of Dijkstra’s single-source shortest-paths algorithm in the class graph.ShortestPaths.
This implementation is needed by the program in order to generate the mazes the diver searches.
In addition, you are likely to find the algorithm useful for other tasks.
Note that the algorithm is to be implemented in a generic way that allows it to be reused in different parts of the program, or even in different programs.
The types of vertices and nodes in the graph are parameters to the algorithm, which means you can’t call methods on them directly.
Instead, the WeightedDigraph interface (and its parent, DirectedGraph) provide the methods you need to navigate the graph.
By reading its methods’ specifications, you might notice that the ShortestPaths class appears to have two “lifecycle stages”—the methods getDistance() and bestPath() may not be invoked until after singleSourceDistances() has been run.
For this reason, you as the implementer should not call these methods while computing shortest paths.
The algorithm uses a priority queue; we have given you a (slow) implementation of the priority queue that should be good enough for this application, but you are welcome to substitute a different one.
Using a different implementation is completely optional.
If you do use one, you must submit the code.
It should be placed in the datastructures package and documented in your reflection.txt”.
Task 2: Test Dijkstra’s algorithm
Having implemented Dijkstra’s algorithm, you must write additional test cases to ensure that your implementation is correct.
Add at least two more test cases to tests/graph/ShortestPathsTests.java.
An example test case has been provided for reference, but it does not provide sufficient coverage.
The A6 program requires a correct implementation of ShortestPaths in order to run, so if you get stuck on this method, seek assistance from consulting early!
Task 3: Improve the use of concurrency
Once you have implemented Dijkstra’s algorithm, it should be possible to run the program and see the graphical user interface.
However, there is a serious inefficiency in the way the program works.
When the GUI is used, the search of the maze is done in a separate concurrent thread, which must wait while the GUI thread completes its animation of the diver walking from one tile to the next.
Waiting is implemented in game.GUIControl.waitForAnimation() as an inefficient spin loop.
Your task is to use the synchronization primitives you have learned about to implement waiting in an efficient way.
You will need to modify not only waitForAnimation() but also gui.GUI.finishAnimating(), which is called when animations are complete.
This task is complicated somewhat by the fact that the program can be run without any graphical user interface (useful for testing or measuring performance).
In this case, there would be no GUI object to pass to GUIControl.
While the implementer could have accepted null, the use of null in Java often leads to bugs, since developers don’t know when to expect it.
So instead this code uses a class called Maybe to explicitly represent a value that may or may not be present.
Read the API documentation for the Maybe class to learn how to access any value contained inside (the thenDo() method in the given code is one example).
This task does not have to be completed in order to move on to the next tasks; the program should work, albeit inefficiently, with the code we give you. Be prepared to have your computer plugged in, though, because the spin loop will use 100% of your CPU until this task is complete. (You can see this in Activity Monitor or Task Manager or the equivalent, depending on your operating system.) You can expect that your computer will also run noticeably cooler when this task is complete!
Part 2: McDiver
In part 2, you will complete the following tasks in diver/McDiver.java:
Task 1: Seek Phase
On the way to the ring (see figure below), the layout of the sewer system is unknown. McDiver does not know the full maze, but only about the place on which McDiver is standing and the immediately neighboring ones (and perhaps others that McDiver remembers). McDiver also knows the Manhattan distance to the ring (note: the length of the path may be longer). When standing on the ring, the distance is 0.
The figure below corresponds to what you will see in your GUI when running the program. In the lower left, McDiver can be seen diving into the sewer with feet sticking out. This image indicates McDiver’s starting point. Currently, McDiver has traversed all the pink tiles on the way to the ring. The figure with the yellow hat is McDiver; to McDiver’s east, the glowing ring can be seen.
To find the ring, McDiver will potentially have to visit all reachable points in the maze. Fortunately, the maze can be viewed as a graph, and you have seen algorithms for graph traversal! This video on JavaHyperText suggests one way to organize such a traversal (See “dfs walk”).
The goal is to make it to the ring in as few steps as possible.
Write your solution to this part as one or more new methods in class diver.McDiver, then call them from method seek().
Be sure to fully document the specifications for your solution’s methods and to assert any preconditions you impose.
If your solution uses iteration rather than recursion, then document and assert any invariants of your loop.
Trust us—doing this up front will make your life easier.
The vast majority of bugs in code like this come from not understanding and enforcing preconditions.
Consultants will ask to see your specifications before assisting you in diagnosing your solution.
Implement your solution using the methods of the SeekState interface to inspect the maze and to move McDiver:
long currentLocation()- Return the unique identifier associated with McDiver’s current location.
int distanceToRing()- Return McDiver’s current distance along the grid (NOT THE GRAPH) from the ring.
void moveTo(long id)- Change McDiver’s current location to the node given by
id. Collection<NodeStatus> neighbors()- Return an unordered collection of NodeStatus objects associated with all direct neighbors of McDiver’s current location.
Because your seek() method cannot see the whole maze in advance, you are unlikely to get lucky and walk the shortest possible path.
However, there are heuristics you can use to improve your chances of taking a more direct route.
The fewer steps you take beyond the minimum possible, the larger a score multiplier you’ll receive (“Bonus” in the GUI).

Task 2: Scram Phase
Because the sewer system is an unhealthy environment, McDiver must get to the exit of the lower level within a prescribed number of steps, while also trying to pick up treasure on the way. Fortunately, McDiver now has a complete map. See Fig. 2, which also shows the pane on the right of the GUI, giving information about the sewer system. To summarize, the goal of the “scram” phase is to get to the exit within a prescribed number of steps, which will always be possible. In the figure below, the exit/entrance is in the upper-left corner of the sewer system—you see McDiver with feet still showing.
McDiver’s score is the product of these two quantities:
- The value of the coins that McDiver picks up during the scram phase.
- The score multiplier from the seek phase.
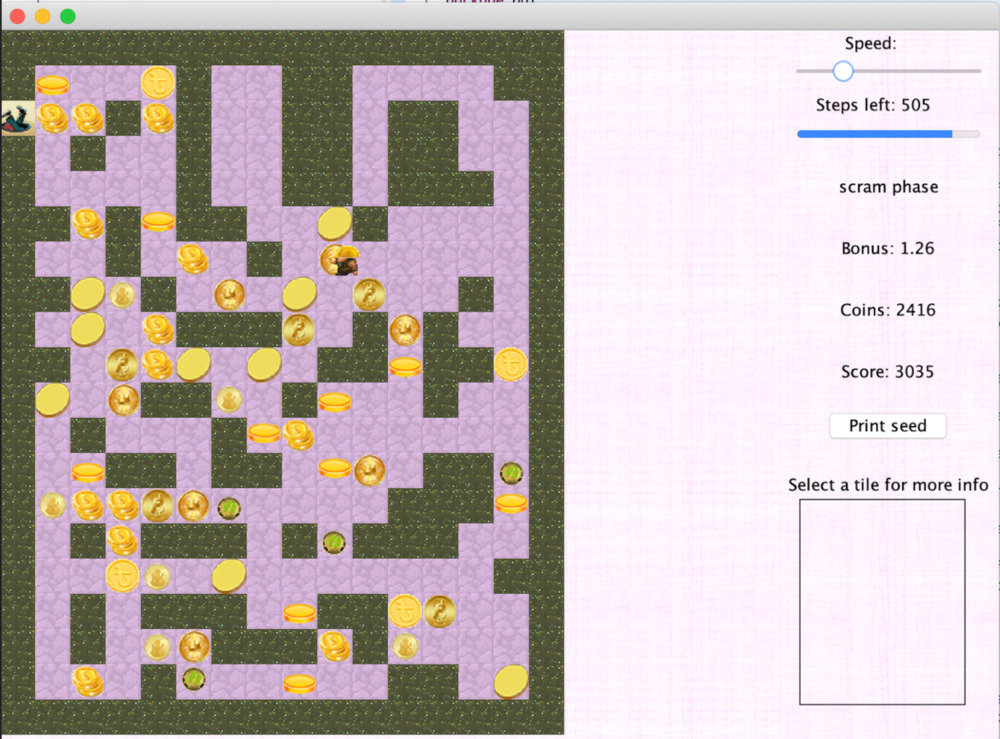
As with the seek phase, implement your solution to this part as new methods in class diver.McDiver, then call them from method scram().
Your methods must have complete specifications, and you should assert any preconditions and invariants.
A good starting point is to write an implementation that takes the shortest path to the exit, which is guaranteed to succeed.
(Hint: use your implementation from Part 1!)
After that, consider how to traverse the sewer system to pick up more coins to optimize your score using more advanced techniques.
However, the most important part is always that McDiver successfully gets to the exit of the sewer system in the prescribed number of steps.
If you improve on your solution, make sure that McDiver never fails to get out in time.
The scram phase is implemented by interacting with the maze and driver using the following methods from the ScramState interface:
Collection<Node> allNodes()- Return a collection containing all the nodes in the graph.
Node currentNode()- Return the `Node`` corresponding to McDiver’s location in the graph.
Node exit()- Return the
Nodeassociated with the exit from the sewer system. void moveTo(Node n)- Change McDiver’s location to
n. int stepsToGo()- Return the steps remaining to get out of the sewer system.
If you want to use your ShortestPaths as part of your solution to scram() (highly recommended), you might find the class game.Maze to be useful.
Structure of Codebase
The structure of the code is shown below.
Most of the files have helper code that you do not have to (and should not) modify.
The file names colored in green have TODOs you have to complete.
Files in blue have main() methods that you can run.
A detailed description of each of the packages is also indicated below. You should also consult the JavaDoc documentation for the code release.
a6/src ├── cms.util │ ├── maybe [dir..] │ └── FastException.java ├── datastructures │ ├── PQueue.java │ └── SlowQueue.java ├── diver │ ├── McDiver.java │ └── SewerDiver.java ├── game │ ├── Main.java │ ├── GameState.java │ ├── GUIControl.java │ ├── Edge.java │ ├── Maze.java │ ├── Node.java │ ├── NodeStatus.java │ ├── Tile.java │ ├── ScramState.java │ ├── SeekState.java │ └── Sewers.java ├── graph │ ├── ShortestPaths.java │ ├── DirectedGraph.java │ └── WeightedGraph.java ├── gui │ ├── GUI.java │ ├── DiverSprite.java │ ├── MazePanel.java │ ├── OptionsPanel.java │ ├── Sprite.java │ └── SelectPanel.java a6/tests ├── graph │ └── ShortestPathsTest.java a6/res [Images needed for GUI] a6/reflection.txt
Here is an overview of all the packages contained in this codebase.
cms.util: Containscms.util.maybe, which implements theMaybetype described earlier. You should use but not modify it.datastructures: This package contains implementations of data structures that can be helpful while implementing your graph search algorithms. If you want to implement a faster priority queue, add it here.diver: This package contains the implementations of graph traversal algorithms used in the McDiver app.- McDiver.java: You will implement the
seek()andscram()phases of this game in this file
- McDiver.java: You will implement the
game: This package contains main game state logic for the McDiver App- GameState.java: The main controller for the game.
- Main.java: Runs the McDiver App. See instructions below for run configurations
graph: This package contains a generic implementation of Dijkstra’s shortest path algorithm that is used by the McDiver app- ShortestPaths.java: You complete the implementation for Dijkstra’s algorithm in this file as part of Task 1
gui: This package contains the GUI implementation for the McDiver App- tests/: This folder contains test harnesses for various other files in this codebase, organized into the same package structure as above
- ShortestPathsTest.java: You will add your tests for Dijkstra’s algorithm in this file
Running Your McDiver Program
The McDiver application can be run from the class game.Main.
Make sure to turn on assertions (VM option -ea) to get more useful feedback.
If you run the program after completing just Part 1, McDiver stands still on the screen and an error message appears telling you that seek() returned at the wrong location.
Some optional flags can be used to run the program in different ways.
--nographicsruns the program in “headless” mode, with no graphical display. This is useful for evaluating performance.-n <count>runs the program count number of times. This option is only available in the headless mode; it is ignored when running in GUI mode. Output is written to the console for each maze, so you know how well you did, and an average score is provided at the end. This is helpful for running your solution many times and comparing different solutions on a large number of different mazes.-s <seed>runs the program with a predefined seed. This allows you to test your solutions on particular mazes that can be challenging or that you might be failing on. It is helpful for debugging. This can be used both with the GUI and in headless mode.--helpreports a usage message.
Scoring
Most of your points on Part 2 come from implementing a solution that always finds the ring and always gets out within the prescribed number of steps. Your priority should be to make sure that your code always does this successfully. If you can always find the ring and always escape, you will get at least 85% of the points for these tasks.
Beyond that basic goal, you can think of ways to optimize the score by taking fewer steps to find the ring and by collecting as much treasure as possible.
Algorithms that find the ring more efficiently or that collect more treasure while escaping will get more points.
Your score will not be determined by comparing to the work of other students.
Full points should be achievable if your solution makes effective use of the ring distance and does a reasonable job of seeking out coins in the scram phase.
Beyond an average score of about 20,000 (i.e. when running with -n 30 -s 1), additional performance is just for bragging rights on our leaderboard.
We will also care about the efficiency of your implementation. On a headless run (no GUI), a single maze should be able to complete within 10 seconds.
Restrictions
-
You must not use any non-constant static variables. Our grading program could run several sewer systems simultaneously, using different threads, and having a
staticfield that can change will be disastrous. -
Import any classes and interfaces that you need from the Java standard library. Don’t try to import any other libraries.
Tips
-
Don’t put all your code directly in the methods
seek()andscram(). Instead, for maximum flexibility, write a dfs walk (or code to scram) in separate well-specified methods. Then, call those methods fromseek()(orscram()). Among other benefits, this will help you manage any recursion you are using, sinceseek()andscram()probably should not be recursive themselves. -
Special maps
You can use the
-soption to select maps in a reproducible way for the purpose of testing. Here are seed values for some interesting maps:- No backtracking to find the ring (no optimization): -280019746129361794
- Backtracking to find the ring (no optimization): 1908492650781828577
- The sewer system built with this seed has no reachable coins: -3026730162232494481
- The only coin is on the tile with the ring, and it is picked up automatically as soon as the scram phase starts: -4004310660161599891
- Trivial scram: 8035820871068432943
- Interesting scram: 2805343804353418701
We expect you to test your submission using these seeds to ensure that your solution is robust. There are special deductions associated with failing to run on these special maps.
What to Submit
Before you submit, make sure you have made a group on CMSX with your partner! (Remember: you are expected to do this before starting work together.) Also make sure to update the file reflection.txt with information like the time you spent and your group’s identification.
Then upload a zip file named “a6.zip” containing at least the following six files: McDiver.java, GUIControl.java, GUI.java, ShortestPaths.java, ShortestPathsTest.java and reflection.txt to Assignment 6 on CMSX before the deadline. The zip file should be structured like the released code, with a top-level a6/ directory. For example, McDiver.java should be in a6/src/diver and ShortestPathsTest.java should be in a6/tests/graph. You may also include in the zip file any extra Java source files that you added for your implementation, in the appropriate directories. Do not change any given code outside of their TODOs—when we test your program, reference implementations of all other classes will be used.
After you submit, CMSX will automatically send your submission to a smoketester. The purpose of the smoketester is to give you confidence that you submitted correctly. You should receive an email from the smoketester shortly after submitting. Read it carefully, and if it doesn’t match your expectations, confirm that you uploaded the intended version of your file and that your ZIP archive is organized correctly (it will be attached to the smoketester feedback).
Good luck, and have fun!
