Self-check exercise: While-loops
-
The value of (π^2)/8 can be approximated by the
series
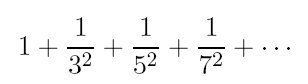
-
We use the above series for approximating (π^2)/8
again
but with a different stopping criterion. Let the sum of the first n terms be
Tn. As n increases one expects the ratio Tn/Tn+1 to approach 1. Write a script to find the smallest n such that the ratio this ratio is greater than 0.9999. Display
n and Tn.
Hint: Now you need to keep track of a current sum and the next sum in the loop. -
Complete the script stepPyramidSkeleton.m to draw a step pyramid, as the one shown below.
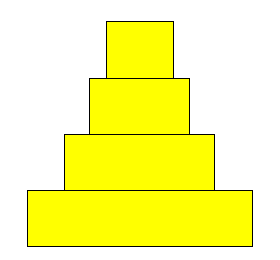
Note: To draw a single rectangle, you can make use of the functionDrawRectthat we have defined for you in file DrawRect.m . To use this function, save this file to your MATLAB working directory and call it from your script with the syntaxDrawRect(a,b,L,H,c)to draw a rectangle with lower-left corner at(a,b)a (horizontal) length L, a height H and color c which should be one of 'r', 'g', 'y'. -
How many rolls of a fair die does one need to accumulate at least 20 points? Of course
one needs at least 4 rolls (as in 6 + 6 + 6 + 2 or 6 + 5 + 4 + 5) and at most 20 rolls
(getting 20 1's in a row). However these sittuations are rather unlikely! Hence, we ask
ourselves: what is the most likely number of times that one has to roll a die to get
20 points? Write a program to answer this question.
- First write a fragment of code that simulates one experiment run, i.e. rolling the die several times until 20 points have been accumulated and counting how many times the die was rolled. Store this count in variable
n - Test it.
- Then insert this fragment in a loop to do many runs (say 10000). Do not forget to reset
nto 0 at the beginning of the loop - Use an array
countsto summarize the results, as follows. Start withcountsbeing a vector of zeros of length 20. After each run increment componentcounts(n)by one if the run tooknrolls of the die. - After running your program,
sum(counts)should equal 10000 (the total number of runs) and[maxcount, maxn] = max(counts)will yield the maximum count and the value ofnfor which this count is obtained.maxnwill be the most likely number of rolls of the die to get 20 points.
- First write a fragment of code that simulates one experiment run, i.e. rolling the die several times until 20 points have been accumulated and counting how many times the die was rolled. Store this count in variable
