- The following program reads an integer k, and outputs all the multiples of k up to 1000.
k = input('Please enter a positive integer smaller than 1000: ');
for j = ______________________
disp(j)
end
-
The following program reads in a real number x and an integer N, and computes the sum
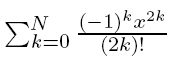 to the first N terms. (This sum converges to cos(x) as N→ ∞.)
to the first N terms. (This sum converges to cos(x) as N→ ∞.)
x = input('Please input a real number between 0 and pi/2: ');
N = input('Please input a positive integer: ');
sum = 0;
for j = _______________________
sum = sum + (-1)^(j/2) * x^j / factorial(j);
end
disp(sprintf('The sum of the first %d terms is %12.8f\n', N, sum))
-
The following does the same thing as the previous part, but this time we are not allowed to use exponentiation and the factorial function, and must compute these explicitly.
x = input('Please input a real number between 0 and pi/2: ');
N = input('Please input a positive integer: ');
sum = 1; % Explicitly assign the first term (when j=0)
sign = 1; % The sign of a term, either 1 or -1
jfact = 1; % Current value of j!
xtoj = 1; % Current value of x^j
for j = _________________________
sign = ________________________________;
jfact = ________________________________;
xtoj = ________________________________;
sum = ____________________________________________;
end
disp(sprintf('The sum of the first %d terms is %12.8f\n', N, sum))
-
Ann and Bob each flips a coin twice in a game. Ann wins if she gets two tails; Bob wins if his two flips are different. If there is a tie, then neither player wins the game.
- Write a program to estimate Ann and Bob's winning probabilities. Your program should do this by simulating the game first 100, then 1000 and finally 10000 times and determing what percentage of the time Ann and Bob win. Your program should report all three results after a single run without you having to manually any parameters between runs.
- Suppose Ann and Bob flips an unfair coin-tails shows up twice as often as heads. What are the winning probabilities?
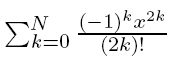 to the first N terms. (This sum converges to cos(x) as N→ ∞.)
to the first N terms. (This sum converges to cos(x) as N→ ∞.)
